TL;DR#
Current large language models (LLMs) exhibit impressive reasoning capabilities but often struggle with complex problems, particularly those requiring extensive reasoning steps. Existing approaches often rely on external verification or extensive sampling, leading to inefficiencies. This paper tackles these limitations by introducing Satori, a novel LLM trained using a two-stage paradigm. The first stage focuses on internalizing a new reasoning format called Chain-of-Action-Thought (COAT), while the second leverages reinforcement learning to improve the model’s ability to self-reflect and explore alternative solutions.
The proposed method results in a single LLM capable of autoregressive search without external guidance. Satori surpasses state-of-the-art performance on multiple mathematical reasoning benchmarks and generalizes well to other tasks. This represents a significant advance in LLM reasoning, offering a more efficient and effective method for tackling complex problems. The researchers’ commitment to open-sourcing the model and data will further accelerate research and foster community collaboration.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language models (LLMs) and reasoning. It introduces a novel training method that significantly improves LLMs’ reasoning capabilities, addressing a key challenge in the field. The open-sourcing of the model and data further accelerates research progress and fosters collaboration. The innovative approach of using chain-of-action-thought (COAT) and reinforcement learning offers new avenues for future research on enhancing LLMs for complex reasoning tasks.
Visual Insights#

🔼 This figure illustrates the two-stage training process of the Satori model. The first stage, Format Tuning (FT), uses imitation learning on a small set of demonstration trajectories to teach the model the Chain-of-Action-Thought (COAT) reasoning format. The second stage, Self-improvement, employs large-scale reinforcement learning to enhance the model’s ability to reason using the COAT format, allowing it to learn self-reflection and self-exploration strategies. This leads to significant improvements in the model’s ability to solve complex problems.
read the caption
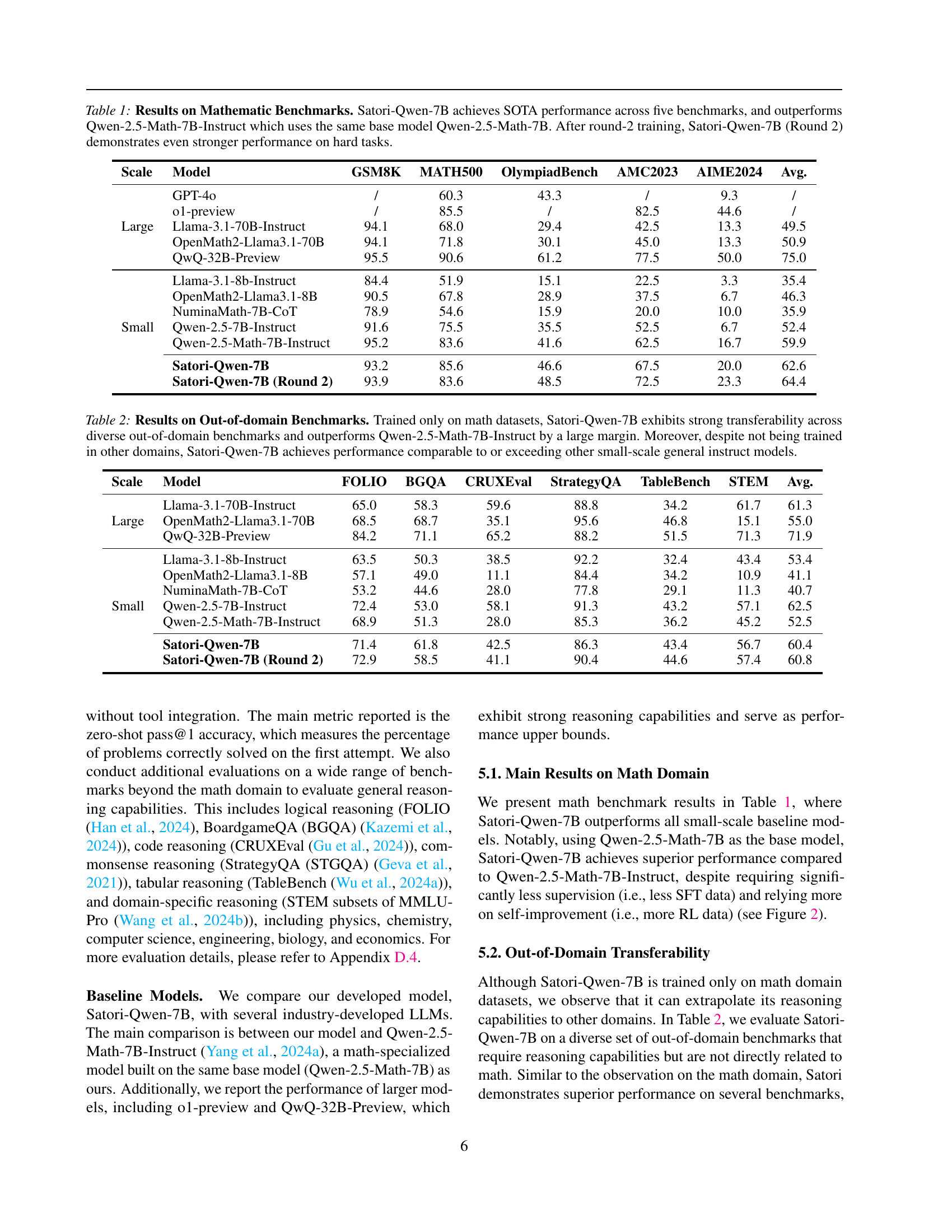
Figure 1: A High-level Overview of Satori Training Framework: Format Tuning (FT) + Self-improvement. First, Satori learns COAT reasoning format through imitation learning on small-scale demonstration trajectories. Next, Satori further leverages COAT reasoning format to self-improve via large-scale reinforcement learning.
| Scale | Model | GSM8K | MATH500 | OlympiadBench | AMC2023 | AIME2024 | Avg. |
| Large | GPT-4o | / | 60.3 | 43.3 | / | 9.3 | / |
| o1-preview | / | 85.5 | / | 82.5 | 44.6 | / | |
| Llama-3.1-70B-Instruct | 94.1 | 68.0 | 29.4 | 42.5 | 13.3 | 49.5 | |
| OpenMath2-Llama3.1-70B | 94.1 | 71.8 | 30.1 | 45.0 | 13.3 | 50.9 | |
| QwQ-32B-Preview | 95.5 | 90.6 | 61.2 | 77.5 | 50.0 | 75.0 | |
| Small | Llama-3.1-8b-Instruct | 84.4 | 51.9 | 15.1 | 22.5 | 3.3 | 35.4 |
| OpenMath2-Llama3.1-8B | 90.5 | 67.8 | 28.9 | 37.5 | 6.7 | 46.3 | |
| NuminaMath-7B-CoT | 78.9 | 54.6 | 15.9 | 20.0 | 10.0 | 35.9 | |
| Qwen-2.5-7B-Instruct | 91.6 | 75.5 | 35.5 | 52.5 | 6.7 | 52.4 | |
| Qwen-2.5-Math-7B-Instruct | 95.2 | 83.6 | 41.6 | 62.5 | 16.7 | 59.9 | |
| Satori-Qwen-7B | 93.2 | 85.6 | 46.6 | 67.5 | 20.0 | 62.6 | |
| Satori-Qwen-7B (Round 2) | 93.9 | 83.6 | 48.5 | 72.5 | 23.3 | 64.4 |
🔼 This table presents the performance of various large language models (LLMs) on five mathematical reasoning benchmarks: GSM8K, MATH500, OlympiadBench, AMC2023, and AIME2024. The results showcase Satori-Qwen-7B’s state-of-the-art performance, surpassing other models, especially Qwen-2.5-Math-7B-Instruct, which shares the same base model. Furthermore, the table highlights the improved performance of Satori-Qwen-7B after a second round of training, demonstrating its ability to handle more challenging problems.
read the caption
Table 1: Results on Mathematic Benchmarks. Satori-Qwen-7B achieves SOTA performance across five benchmarks, and outperforms Qwen-2.5-Math-7B-Instruct which uses the same base model Qwen-2.5-Math-7B. After round-2 training, Satori-Qwen-7B (Round 2) demonstrates even stronger performance on hard tasks.
In-depth insights#
LLM Reasoning#
LLM reasoning is a rapidly evolving field, focusing on enhancing the ability of large language models (LLMs) to perform complex reasoning tasks. Current approaches often involve prompting techniques, such as Chain-of-Thought (CoT), which guide the LLM to generate intermediate reasoning steps, thereby improving accuracy. However, these methods may still struggle with complex problems or exhibit limitations in generalizing to unseen domains. Reinforcement learning (RL) offers a promising avenue for improving LLM reasoning by training the model to maximize rewards associated with correct reasoning. This approach can internalize the search process, enabling autoregressive search capabilities within a single LLM and reducing reliance on external feedback mechanisms. Research is actively exploring different RL strategies, including those that encourage self-reflection and exploration of alternative solution paths. Despite these advances, challenges remain, such as handling sparse rewards and ensuring effective generalization. Future research directions include developing more sophisticated reward functions, designing more robust training paradigms, and investigating the interplay between different reasoning mechanisms within LLMs.
COAT Mechanism#
The Chain-of-Action-Thought (COAT) mechanism is a novel approach to enhance Large Language Model (LLM) reasoning capabilities. It extends the Chain-of-Thought (CoT) prompting technique by introducing meta-action tokens that allow the LLM to perform self-reflection, self-correction, and exploration of alternative solutions. Instead of passively following a linear reasoning path, the LLM actively manages its reasoning process through these meta-actions. This introduces a degree of internal search, overcoming limitations of prior CoT methods which rely on extensive external sampling or feedback loops. The COAT mechanism is particularly effective in addressing complex problems where iterative refinement and error correction are necessary, leading to a more robust and accurate reasoning process. Its integration with reinforcement learning further strengthens the LLM’s capacity for self-improvement and generalization to out-of-domain tasks, showcasing its potential as a powerful framework for building more advanced reasoning abilities into LLMs. Two-stage training — format tuning and self-improvement — further enhances COAT’s effectiveness.
Two-Stage Training#
The paper’s two-stage training approach is a key innovation, addressing limitations in directly training LLMs for complex reasoning. The first stage, format tuning, uses imitation learning on a small dataset of demonstration trajectories to familiarize the model with the chain-of-action-thought (COAT) reasoning format. This efficiently bootstraps the process by minimizing the initial training burden of teaching the LLM this novel reasoning structure. The second stage, self-improvement, leverages reinforcement learning to significantly enhance the LLM’s reasoning capabilities. Crucially, it tackles the sparse reward challenge of long-horizon reasoning tasks by incorporating “restart and explore” techniques. This allows the model to recover from errors and explore alternative solutions, leading to better generalization and performance. This two-stage approach thus combines efficient initial training with a powerful self-improvement mechanism resulting in a robust and effective LLM reasoning system.
Satori’s Abilities#
The paper showcases Satori’s impressive capabilities in mathematical reasoning and its ability to generalize to other domains. Satori’s strength lies in its novel Chain-of-Action-Thought (COAT) reasoning mechanism, which allows for self-reflection and exploration of alternative solution strategies. Unlike previous methods relying on external verification, Satori internalizes these search capabilities, achieving higher efficiency. The two-stage training paradigm—format tuning followed by reinforcement learning—is instrumental in enabling Satori’s superior performance and generalization. The results demonstrate state-of-the-art performance on several mathematical benchmarks, highlighting Satori’s effectiveness. Furthermore, Satori’s strong generalization to out-of-domain tasks showcases its robust reasoning capabilities beyond specialized mathematical domains. This is a significant contribution in the field of large language models, demonstrating the potential for single-model autoregressive search to significantly enhance reasoning abilities. The open-sourcing of the model and data further strengthens Satori’s contribution to the research community.
Future of Search#
The “Future of Search” in light of this research paper points towards a paradigm shift. Autoregressive search, internalized within a single LLM, is presented as a more efficient and cost-effective alternative to current two-player systems. This shift necessitates further exploration of innovative training paradigms like reinforcement learning, focusing on self-improvement and exploration of new reasoning strategies. Meta-action tokens and improved reward models could enhance the sophistication of autoregressive search, improving the accuracy and generalizability of LLMs reasoning abilities. Addressing challenges such as sparse rewards and long horizons in reinforcement learning is crucial for this advancement. This evolution signifies a move towards more autonomous and efficient LLMs capable of complex reasoning tasks, potentially leading to a significant advancement in search technology and problem solving across various domains.
More visual insights#
More on figures

🔼 This figure compares the training data used for two language models: Satori-Qwen-7B and Qwen-2.5-Math-7B-Instruct. It highlights that Satori-Qwen-7B, despite being a smaller model, requires substantially less supervised fine-tuning (FT) data. The difference is visually represented on a logarithmic scale, illustrating that the majority of Satori-Qwen-7B’s training relies on large-scale reinforcement learning (RL) for self-improvement, unlike Qwen-2.5-Math-7B-Instruct which uses substantially more supervised fine-tuning.
read the caption
Figure 2: Number of Training Samples of Satori-Qwen-7B and Qwen-2.5-Math-7B-Instruct. Satori-Qwen-7B requires significantly less supervision (small-scale FT) and relies more on self-improvement (large-scale RL).

🔼 This figure illustrates the relationship between the policy accuracy, response length (measured in the number of tokens), and RL training time compute. The x-axis represents the RL training steps. The y-axis shows two lines: one representing policy accuracy (left y-axis) and the other representing response length (right y-axis). The figure demonstrates that as the RL training progresses (more compute time is used), the policy accuracy increases, indicating that the model’s reasoning improves. Simultaneously, the response length also increases, meaning that the model engages in longer and more complex reasoning processes to achieve better accuracy. This supports the paper’s claim that reinforcement learning enables the model (Satori) to improve its reasoning through longer and more sophisticated thought processes.
read the caption
Figure 3: Policy Training Acc. & Response length v.s. RL Train-time Compute. Through RL training, Satori learns to improve its reasoning performance through longer thinking.

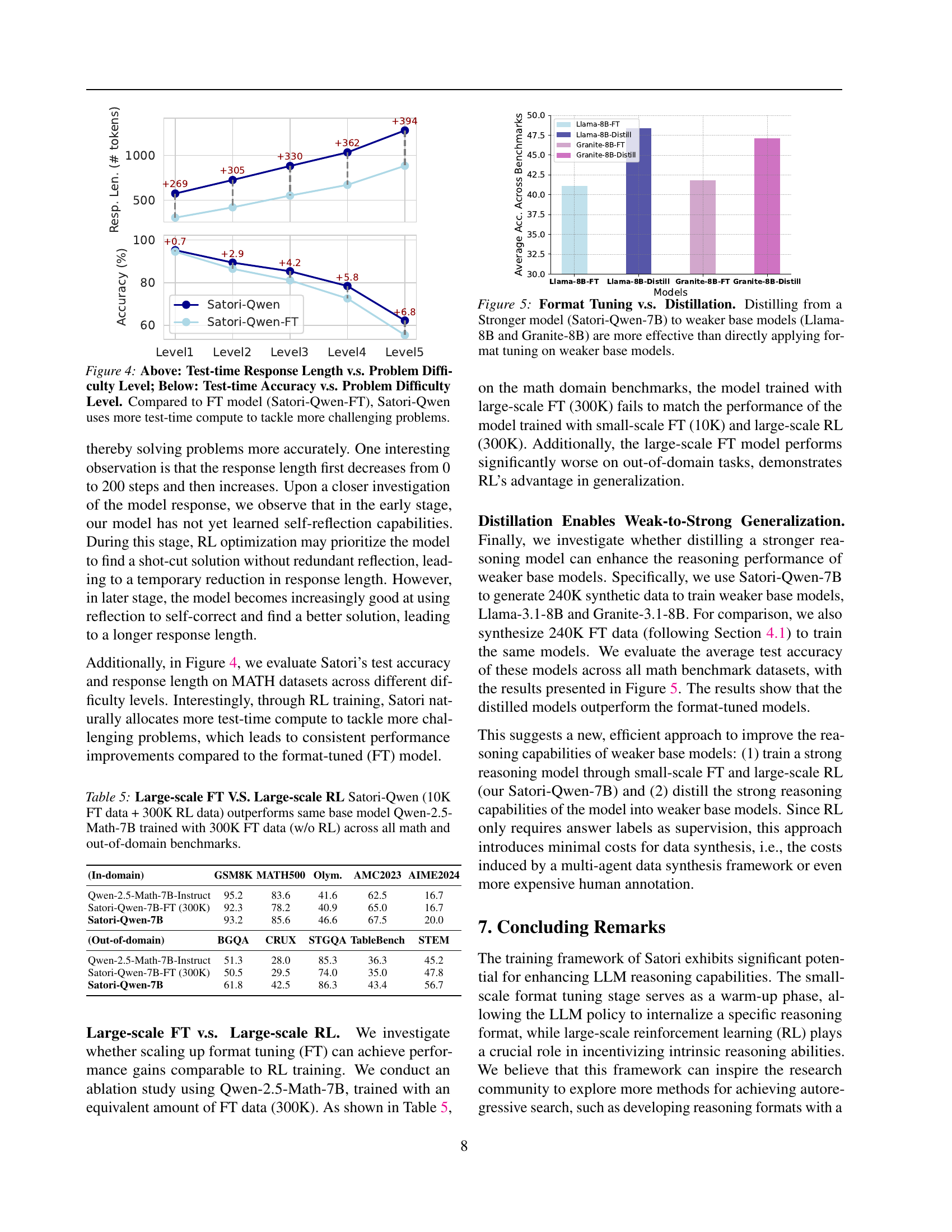
🔼 This figure shows the relationship between test-time response length and accuracy with problem difficulty levels. The top panel plots the average number of tokens generated during inference (test-time response length) against problem difficulty, categorized into five levels (Level 1 to Level 5, with Level 5 being the most difficult). The bottom panel plots the corresponding test-time accuracy for each difficulty level. The figure compares the performance of the Satori-Qwen model with that of the Satori-Qwen-FT model, highlighting how Satori-Qwen uses significantly more compute (longer response lengths) to achieve better accuracy on harder problems compared to the Satori-Qwen-FT model.
read the caption
Figure 4: Above: Test-time Response Length v.s. Problem Difficulty Level; Below: Test-time Accuracy v.s. Problem Difficulty Level. Compared to FT model (Satori-Qwen-FT), Satori-Qwen uses more test-time compute to tackle more challenging problems.

🔼 This figure compares two different methods of improving weaker language models (Llama-8B and Granite-8B): format tuning and distillation. Format tuning involves directly training the weaker models on a dataset of correctly formatted reasoning examples. Distillation, on the other hand, involves training a stronger model (Satori-Qwen-7B) and then transferring its knowledge to the weaker models. The figure shows that distillation is a more effective method, resulting in significantly better performance on the benchmark tasks.
read the caption
Figure 5: Format Tuning v.s. Distillation. Distilling from a Stronger model (Satori-Qwen-7B) to weaker base models (Llama-8B and Granite-8B) are more effective than directly applying format tuning on weaker base models.

🔼 This figure shows an example of Satori’s mathematical reasoning process. Satori is given a problem and generates a step-by-step solution. Unlike other LLMs, Satori includes self-verification steps: it checks each intermediate step to ensure correctness before proceeding to the next step. The figure visually depicts the flow of this process, highlighting Satori’s self-reflection and correction of errors within its reasoning chain.
read the caption
Figure 6: Math Domain Example. Satori verifies the correctness of the intermediate steps and proceeds to the next reasoning step.

🔼 This figure shows an example of Satori’s reasoning process on a math problem from the AIME2024 benchmark. The initial solution attempts to solve the problem through a complex, multi-step approach that ultimately contains errors. Satori’s ‘self-reflection’ capability is demonstrated as it identifies those errors and proceeds to generate a second, more concise and accurate solution. This illustrates Satori’s ability to self-correct and improve its reasoning through internal review.
read the caption
Figure 7: Math Domain Example. Satori identifies the mistakes in the previous solution and proposes an alternative correct solution.

🔼 This figure shows an example of Satori’s reasoning process on a mathematical problem from the MATH dataset. The model initially attempts a solution, but then uses a meta-action token (reflect) to trigger a self-check. Recognizing a flaw in the initial approach, it then explicitly starts a new, different solution path to arrive at the correct answer, demonstrating the model’s self-reflection and strategy adaptation capabilities.
read the caption
Figure 8: Math Domain Example. Satori verifies the correctness of previous solution and initiates a different solution.

🔼 This figure showcases Satori’s problem-solving process on a math problem. Initially, Satori provides a solution, but then uses its self-reflection capabilities to identify areas where the solution could be improved. This leads to a second attempt where it presents a more concise and arguably more elegant method to arrive at the same correct answer. The figure highlights Satori’s capacity for iterative refinement and its ability to explore alternative solution strategies, even after reaching a valid answer.
read the caption
Figure 9: Math Domain Example. Satori verifies the correctness of previous solution and further explores a simpler solution.

🔼 This figure shows an example of Satori’s mathematical reasoning process. In the first stage, Satori checks the correctness of intermediate steps in its solution. However, Satori later identifies that its initial approach was flawed. It then uses this realization to correct its solution and propose a new, more accurate solution method.
read the caption
Figure 10: Math Domain Example. 1) Satori verifies the correctness of intermediate steps in early stage. 2) Satori realizes that the pervious solution is actually erroneous and then proposes an alternative correct solution.

🔼 This figure showcases Satori’s reasoning process on an out-of-domain problem from the StrategyQA benchmark. The example demonstrates Satori’s ability to identify errors in its own reasoning steps. First, Satori provides an initial solution attempt but realizes there are flaws. It then initiates a second solution, which corrects the earlier mistakes and proceeds to a completely different, correct final answer. This highlights Satori’s capacity for self-correction and exploring alternative strategies to reach a solution, even in unfamiliar domains.
read the caption
Figure 11: Out-of-domain Example. 1) Satori identifies the potential mistakes in intermediate steps and initiates another solution. 2) Satori realizes that the pervious solution is still erroneous and then proposes an alternative correct solution.

🔼 This figure showcases an example from the StrategyQA dataset, demonstrating Satori’s ability to identify and correct errors during complex reasoning tasks. Initially, Satori attempts to solve the problem and recognizes some flaws mid-process. It then proposes an alternative solution, highlighting its capacity for self-correction and refinement. The example shows multiple self-reflection processes and a change of approach to achieve the correct answer, demonstrating Satori’s capabilities to tackle out-of-domain tasks that involve several logical reasoning steps.
read the caption
Figure 12: Out-of-domain Example. Satori identifies the potential mistakes in intermediate steps and initiates another correct solution.

🔼 This figure shows an example of Satori’s reasoning process on an out-of-domain problem from the MMLUPro Economics section. In the initial phase (1), Satori methodically checks the steps of its solution, verifying their accuracy. However, in the later phase (2), Satori identifies an error in its initial approach and proposes an alternative solution that leads to the correct answer. This highlights the model’s capacity for self-correction and refinement throughout the reasoning process.
read the caption
Figure 13: Out-of-domain Example. 1) Satori verifies the correctness of intermediate steps in early stage. 2) Satori realizes that the pervious solution is actually erroneous and then proposes an alternative correct solution.

🔼 This figure displays an example of Satori’s reasoning process on an out-of-domain problem from the MMLUPro Economics benchmark. The figure showcases Satori’s ability to engage in multiple self-reflection processes during intermediate steps. Instead of directly reaching a conclusion, Satori pauses at various points in its reasoning to re-evaluate its progress and identify potential errors or inefficiencies. This demonstrates its capacity for self-correction and refinement, a key aspect of its autoregressive search capability.
read the caption
Figure 14: Out-of-domain Example. Satori engages in multiple self-reflection processes during intermediate reasoning steps.

🔼 This figure shows an example of Satori’s reasoning process on an out-of-domain problem from the CRUXEval benchmark. The example demonstrates two key aspects of Satori’s capabilities. First, it highlights Satori’s ability to verify the correctness of its intermediate reasoning steps. The model initially checks its work, identifying that the reasoning is proceeding along a valid path. Second, and more importantly, the figure showcases Satori’s ability to identify and correct errors in its own reasoning. After successfully verifying the initial steps, Satori realizes a mistake has been made and proposes a completely different, correct solution to the problem.
read the caption
Figure 15: Out-of-domain Example. 1) Satori verifies the correctness of intermediate steps in early stage. 2) Satori realizes that the pervious solution is actually erroneous and then proposes an alternative correct solution.

🔼 This figure shows an example of Satori’s reasoning process on an out-of-domain problem from the TableBench dataset. The initial solution attempts to calculate the average prominence of mountain peaks in the Democratic Republic of the Congo with elevations above 3000 meters. However, it incorrectly includes a peak with an elevation below the threshold. Satori then identifies this error in its initial solution, corrects the mistake by excluding the erroneous peak from the calculation, and provides a revised solution reflecting the correct calculation of the average prominence.
read the caption
Figure 16: Out-of-domain Example. Satori identifies the mistakes in previous solution and proposes an alternative correct solution.

🔼 This figure illustrates the process of generating high-quality demonstration trajectories for training. It starts with a generator producing multiple reasoning attempts for a given problem. These attempts are then evaluated by a critic, which identifies errors in incorrect solutions and suggests corrections. Correct solutions receive verification. The generator then uses this feedback to refine its incorrect attempts. This iterative refinement process (up to ’m’ iterations) results in improved trajectories. Finally, a reward model selects the best trajectories to create the final synthetic training dataset, 𝒟syn.
read the caption
Figure 17: Demonstration Trajectories Synthesis. First, multiple initial reasoning trajectories are sampled from the generator and sent to critic to ask for feedback. The critic model identifies the mistake for trajectories with incorrect final answers and proposes an alternative solution. For trajectories with correct final answers, the critic model provides verification of its correctness. Based on the feedback, the generator self-refines its previous trajectories, and the incorrect trajectories are sent to the critic again for additional feedback with maximum m𝑚mitalic_m iterations. At each step, those trajectories with successful refinements are preserved and finally, a reward model rates and collects high-quality demonstration trajectories to form the synthetic dataset 𝒟synsubscript𝒟syn\mathcal{D}_{\text{syn}}caligraphic_D start_POSTSUBSCRIPT syn end_POSTSUBSCRIPT.
More on tables
| Scale | Model | FOLIO | BGQA | CRUXEval | StrategyQA | TableBench | STEM | Avg. |
| Large | Llama-3.1-70B-Instruct | 65.0 | 58.3 | 59.6 | 88.8 | 34.2 | 61.7 | 61.3 |
| OpenMath2-Llama3.1-70B | 68.5 | 68.7 | 35.1 | 95.6 | 46.8 | 15.1 | 55.0 | |
| QwQ-32B-Preview | 84.2 | 71.1 | 65.2 | 88.2 | 51.5 | 71.3 | 71.9 | |
| Small | Llama-3.1-8b-Instruct | 63.5 | 50.3 | 38.5 | 92.2 | 32.4 | 43.4 | 53.4 |
| OpenMath2-Llama3.1-8B | 57.1 | 49.0 | 11.1 | 84.4 | 34.2 | 10.9 | 41.1 | |
| NuminaMath-7B-CoT | 53.2 | 44.6 | 28.0 | 77.8 | 29.1 | 11.3 | 40.7 | |
| Qwen-2.5-7B-Instruct | 72.4 | 53.0 | 58.1 | 91.3 | 43.2 | 57.1 | 62.5 | |
| Qwen-2.5-Math-7B-Instruct | 68.9 | 51.3 | 28.0 | 85.3 | 36.2 | 45.2 | 52.5 | |
| Satori-Qwen-7B | 71.4 | 61.8 | 42.5 | 86.3 | 43.4 | 56.7 | 60.4 | |
| Satori-Qwen-7B (Round 2) | 72.9 | 58.5 | 41.1 | 90.4 | 44.6 | 57.4 | 60.8 |
🔼 This table presents the results of evaluating the Satori-Qwen-7B model on various out-of-domain benchmarks. Despite being trained solely on mathematical datasets, Satori-Qwen-7B demonstrates strong generalization capabilities, outperforming the Qwen-2.5-Math-7B-Instruct model (which uses the same base model but with different training) across multiple benchmarks. Furthermore, Satori-Qwen-7B’s performance is comparable to or even surpasses other small-scale, general-purpose instruction-tuned LLMs, highlighting its ability to transfer knowledge gained from math reasoning to other diverse reasoning tasks.
read the caption
Table 2: Results on Out-of-domain Benchmarks. Trained only on math datasets, Satori-Qwen-7B exhibits strong transferability across diverse out-of-domain benchmarks and outperforms Qwen-2.5-Math-7B-Instruct by a large margin. Moreover, despite not being trained in other domains, Satori-Qwen-7B achieves performance comparable to or exceeding other small-scale general instruct models.
| Model | GSM8K | MATH500 | Olym. | AMC2023 | AIME2024 |
| Qwen-2.5-Math-7B-Instruct | 95.2 | 83.6 | 41.6 | 62.5 | 16.7 |
| Qwen-7B-CoT (SFT+RL) | 93.1 | 84.4 | 42.7 | 60.0 | 10.0 |
| Satori-Qwen-7B | 93.2 | 85.6 | 46.6 | 67.5 | 20.0 |
🔼 This table compares the performance of two models: Satori-Qwen-7B, trained using the Chain-of-Action-Thought (COAT) reasoning format, and Qwen-7B-CoT, trained using the classical Chain-of-Thought (CoT) reasoning format. Both models use the same base model, Qwen-2.5-Math-7B. The table shows that Satori-Qwen-7B, trained with the COAT format, outperforms Qwen-7B-CoT, trained with the classical CoT format, across multiple mathematical reasoning benchmarks. This highlights the advantage of the COAT reasoning format in enhancing the reasoning capabilities of LLMs.
read the caption
Table 3: COAT Training v.s. CoT Training. Qwen-2.5-Math-7B trained with COAT reasoning format (Satori-Qwen-7B) outperforms the same base model but trained with classical CoT reasoning format (Qwen-7B-CoT)
| Model | In-Domain | Out-of-Domain | ||||
| MATH500 | OlympiadBench | MMLUProSTEM | ||||
| TF | FT | TF | FT | TF | FT | |
| Satori-Qwen-7B-FT | 79.4% | 20.6% | 65.6% | 34.4% | 59.2% | 40.8% |
| Satori-Qwen-7B | 39.0% | 61.0% | 42.1% | 57.9% | 46.5% | 53.5% |
🔼 This table presents the self-correction capabilities of the Satori model. It shows the percentage of times the model successfully corrected an incorrect answer to a correct one (positive self-correction, F→T) versus the percentage of times it changed a correct answer to an incorrect one (negative self-correction, T→F). Results are shown for both in-domain (MATH500 and OlympiadBench) and out-of-domain (MMLUProSTEM) tasks, highlighting the model’s ability to self-correct across various problem types. The ‘FT’ version refers to the model after only format tuning, demonstrating the improvement gained through reinforcement learning.
read the caption
Table 4: Satori’s Self-correction Capability. T→→\rightarrow→F: negative self-correction; F→→\rightarrow→T: positive self-correction.
| (In-domain) | GSM8K | MATH500 | Olym. | AMC2023 | AIME2024 |
| Qwen-2.5-Math-7B-Instruct | 95.2 | 83.6 | 41.6 | 62.5 | 16.7 |
| Satori-Qwen-7B-FT (300K) | 92.3 | 78.2 | 40.9 | 65.0 | 16.7 |
| Satori-Qwen-7B | 93.2 | 85.6 | 46.6 | 67.5 | 20.0 |
| (Out-of-domain) | BGQA | CRUX | STGQA | TableBench | STEM |
| Qwen-2.5-Math-7B-Instruct | 51.3 | 28.0 | 85.3 | 36.3 | 45.2 |
| Satori-Qwen-7B-FT (300K) | 50.5 | 29.5 | 74.0 | 35.0 | 47.8 |
| Satori-Qwen-7B | 61.8 | 42.5 | 86.3 | 43.4 | 56.7 |
🔼 This table compares the performance of two models: Satori-Qwen, trained with a small amount of supervised fine-tuning (10K data points) followed by a large amount of reinforcement learning (300K data points); and Qwen-2.5-Math-7B, trained solely with supervised fine-tuning using a much larger dataset (300K data points). The comparison is performed across a variety of mathematical and non-mathematical reasoning benchmarks. The results demonstrate that incorporating reinforcement learning significantly improves the model’s performance, as Satori-Qwen outperforms Qwen-2.5-Math-7B across all benchmarks.
read the caption
Table 5: Large-scale FT V.S. Large-scale RL Satori-Qwen (10K FT data + 300K RL data) outperforms same base model Qwen-2.5-Math-7B trained with 300K FT data (w/o RL) across all math and out-of-domain benchmarks.
| Bonus Scale | GSM8K | MATH500 | Olym. | AMC2023 | AIME2024 |
| 0.0 | 93.6 | 84.4 | 48.9 | 62.5 | 16.7 |
| 0.5 (default) | 93.2 | 85.6 | 46.6 | 67.5 | 20.0 |
🔼 This table presents the results of an ablation study conducted to evaluate the impact of the reflection bonus on the model’s performance. The reflection bonus is a reward mechanism introduced to encourage the model to engage in self-reflection during the reasoning process. The study compares the model’s performance with the reflection bonus set to 0.0 and 0.5 (default), across various math reasoning benchmarks, including GSM8K, MATH500, OlympiadBench, AMC2023, and AIME2024. The results show that the default value of 0.5 yields better performance, particularly on challenging benchmarks like AMC2023 and AIME2024.
read the caption
Table 6: Ablation Study on Reflection Bonus.
Full paper#