TL;DR#
Current large language models (LLMs) excel at reasoning when provided with step-by-step explanations (chain-of-thought prompting). However, this method leads to lengthy inputs, increasing computational costs. This paper tackles this issue by focusing on the efficiency problem of chain-of-thought prompting. The core problem is that using many words for explanation consumes lots of computational resources and increases response time.
This research introduces a hybrid approach that uses latent discrete tokens (generated by VQ-VAE) to partially represent the initial reasoning steps. This significantly reduces the input length. The researchers trained the model using a random mixing strategy of latent and text tokens, adapting quickly to new tokens and achieving significant performance gains in various benchmarks (Math, GSM8K, and a fresh Gaokao Math dataset). The experiments show that the proposed method not only improved performance but also significantly reduced reasoning trace length (on average, 17%).
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language models (LLMs) and reasoning. It addresses the computational cost of chain-of-thought prompting by introducing a novel method to significantly shorten reasoning traces, thus enhancing LLM efficiency and performance. The proposed technique of using latent tokens opens new avenues for research on efficient and effective LLM training and offers a potential solution to improve the overall efficiency of using LLMs for various reasoning and planning tasks. This is highly relevant given the increasing emphasis on reducing the computational footprint of LLMs.
Visual Insights#

🔼 This figure illustrates the method of compressing reasoning traces in the paper by replacing sequences of text tokens with latent tokens. Specifically, it shows an example where 32 consecutive chain-of-thought (CoT) tokens are replaced by two latent tokens. The replacement starts from the left and proceeds to the right up to a predefined point; after that point, the remaining CoT tokens retain their original form. This technique is used to shorten the length of reasoning traces and reduce computational costs while preserving the crucial reasoning information. The chunk size (L) is set to 16, and the compression rate (r) is also 16, indicating that each chunk of 16 tokens is replaced by one latent token.
read the caption
Figure 3.1: An example illustrating our replacement strategy. With chunk size L=16𝐿16L=16italic_L = 16 and compression rate r=16𝑟16r=16italic_r = 16, we encode 32 textual CoT tokens into 2 discrete latent tokens from left to right. The other CoT tokens will remain in their original forms.
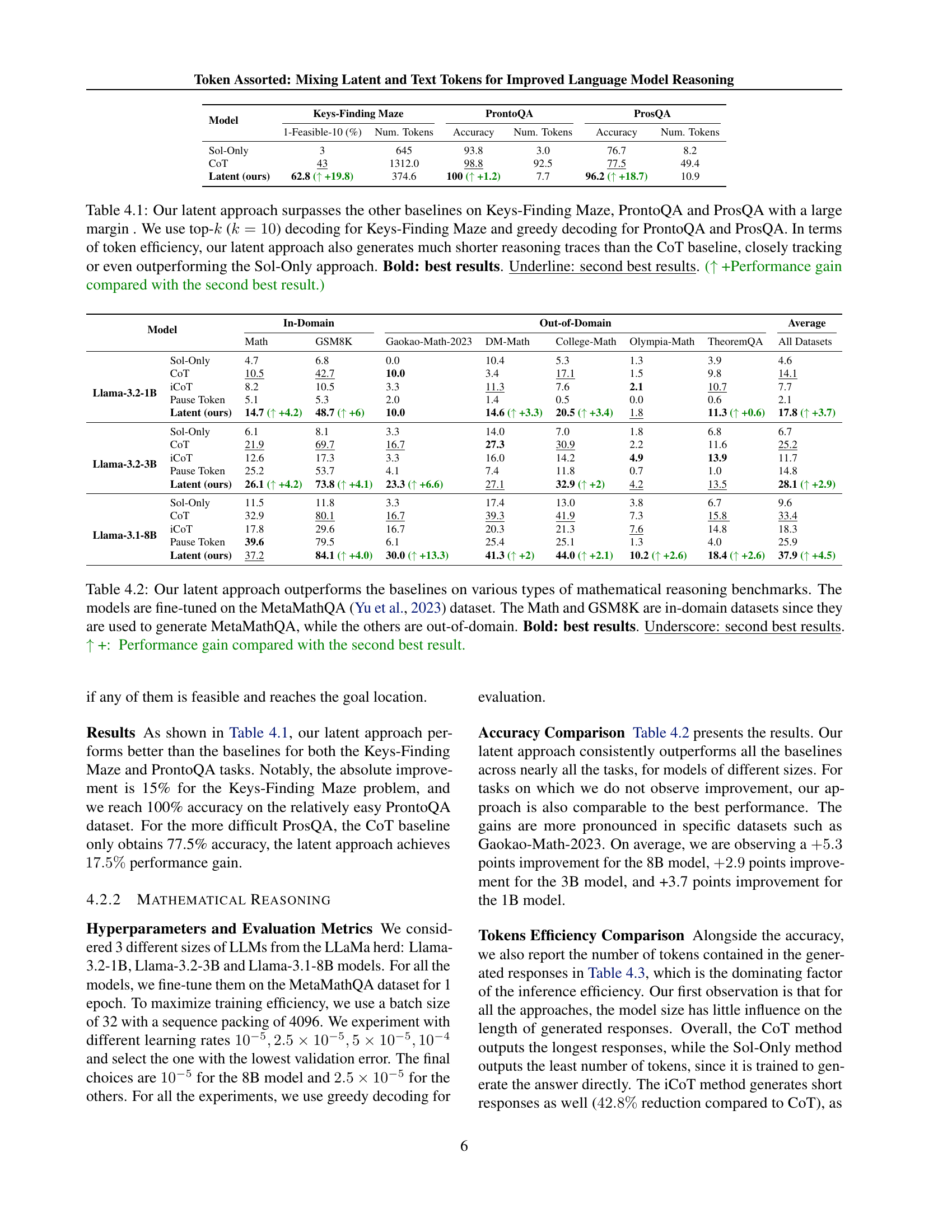
| Model | Keys-Finding Maze | ProntoQA | ProsQA | |||
|---|---|---|---|---|---|---|
| 1-Feasible-10 (%) | Num. Tokens | Accuracy | Num. Tokens | Accuracy | Num. Tokens | |
| Sol-Only | 3 | 645 | 93.8 | 3.0 | 76.7 | 8.2 |
| CoT | 43 | 1312.0 | 98.8 | 92.5 | 77.5 | 49.4 |
| Latent (ours) | 62.8 ( +19.8) | 374.6 | 100 ( +1.2) | 7.7 | 96.2 ( +18.7) | 10.9 |
🔼 Table 4.1 presents a comparison of different methods for solving three reasoning tasks: Keys-Finding Maze, ProntoQA, and ProsQA. The results demonstrate that the proposed ’latent approach’ significantly outperforms existing methods (Sol-Only, CoT, iCoT) in terms of accuracy across all three tasks. Importantly, the table also highlights the efficiency gains of the latent approach. It shows a substantial reduction in the number of tokens required for generating solutions compared to the chain-of-thought (CoT) baseline, while achieving accuracy comparable to or exceeding the Sol-Only approach which generates the shortest traces.
read the caption
Table 4.1: Our latent approach surpasses the other baselines on Keys-Finding Maze, ProntoQA and ProsQA with a large margin . We use top-k𝑘kitalic_k (k=10𝑘10k=10italic_k = 10) decoding for Keys-Finding Maze and greedy decoding for ProntoQA and ProsQA. In terms of token efficiency, our latent approach also generates much shorter reasoning traces than the CoT baseline, closely tracking or even outperforming the Sol-Only approach. Bold: best results. Underline: second best results. (↑↑\uparrow↑ +Performance gain compared with the second best result.)
In-depth insights#
Latent Reasoning#
Latent reasoning, in the context of large language models (LLMs), represents a significant advancement in improving reasoning capabilities. Instead of relying solely on explicit textual reasoning steps, which can be computationally expensive and lengthy, latent reasoning aims to implicitly capture the core essence of reasoning within a compact, compressed representation. This is often achieved through techniques like vector quantization (VQ-VAE), where intermediate reasoning steps are encoded into discrete latent tokens. The key advantage is that these latent representations dramatically reduce the length of reasoning traces processed by the LLM, leading to improved efficiency and potentially better performance on complex reasoning tasks. However, effective utilization of latent reasoning requires careful consideration of several factors. Successful implementation necessitates a robust encoding mechanism that can accurately capture the nuances of the reasoning process and a decoding method that allows the LLM to effectively utilize these latent tokens. Furthermore, training methods must be carefully designed to allow the model to adapt effectively to the presence of unseen latent tokens in the fine-tuning stage, and to balance the benefits of compressed representation against potential information loss.
VQ-VAE Encoding#
The concept of ‘VQ-VAE Encoding’ in the context of a research paper likely refers to the use of a Vector Quantized Variational Autoencoder (VQ-VAE) to generate a compressed, discrete latent representation of input data. This technique is particularly relevant for processing long sequences, such as those found in chain-of-thought (CoT) reasoning traces where many words contribute to textual coherence rather than core reasoning information. The VQ-VAE learns to map sequences of text tokens (the CoT trace) into a lower-dimensional space represented by a discrete set of ’latent tokens’. This compression significantly reduces computational cost and memory usage. A crucial aspect is the use of a codebook, which acts as a lookup table, converting these latent vectors back to meaningful representations. The effectiveness of this approach depends on the VQ-VAE’s ability to capture the essence of the reasoning steps without losing crucial information and the subsequent LLM’s capacity to learn and effectively utilize this compressed representation during reasoning tasks. The success likely hinges on both the design and training of the VQ-VAE as well as the method used to integrate these latent tokens with the remaining parts of the CoT trace during the final model training phase. Therefore, a thorough discussion of architecture, training strategies, and quantitative results evaluating the trade-off between compression and reasoning performance would be expected in a detailed exploration of ‘VQ-VAE Encoding’.
Hybrid Training#
A hypothetical “Hybrid Training” section in a research paper on language models would likely explore methods combining different training paradigms to leverage their respective strengths. One approach could involve pretraining a model on a massive text corpus using standard techniques, followed by finetuning on a smaller, higher-quality dataset designed for specific reasoning tasks. This approach leverages the general knowledge and language proficiency from pretraining, enhancing the model’s ability to reason effectively on more specific tasks during finetuning. Another strategy might involve integrating reinforcement learning (RL) with supervised learning. Initially, supervised learning would establish a baseline performance; RL would then refine the model’s reasoning skills by providing rewards for correct answers and penalties for incorrect ones. This could address the limitations of pure supervised learning by allowing the model to learn from experience and adapt to nuanced problem-solving scenarios. A particularly innovative approach could combine symbolic reasoning methods with neural networks. This could involve incorporating explicit rules and logical structures into the model’s architecture, complementing the network’s ability to learn complex patterns from data. The potential benefits of such an approach are considerable, offering improved robustness and explainability, while also potentially enabling the model to handle more complex and abstract reasoning problems. The challenges would focus on effective integration of these disparate methods and balancing the benefits of each approach. Careful evaluation would be needed to determine the efficacy and efficiency of hybrid approaches compared to traditional methods.
Benchmark Results#
A dedicated ‘Benchmark Results’ section in a research paper would ideally present a comprehensive evaluation of the proposed method against existing state-of-the-art techniques. This would involve selecting relevant and diverse benchmarks, clearly describing the evaluation metrics used, and presenting the results in a clear and easily interpretable format, such as tables and charts. Crucially, the analysis should go beyond simply reporting raw numbers. A robust analysis would delve into the strengths and weaknesses of the proposed method relative to the baselines, exploring possible reasons for superior or inferior performance on specific benchmarks. For instance, if the new method excels on certain tasks but underperforms on others, the reasons for these discrepancies would be investigated and discussed, possibly pointing to areas for future improvement. Statistical significance testing would provide strong evidence supporting the claims of improvement. Further, discussing limitations of the benchmarks themselves and potential biases inherent in the dataset is essential to promote a balanced and credible interpretation of the results. Finally, a detailed discussion of the efficiency and resource requirements of the new method, compared to existing methods, would provide a holistic perspective.
Token Efficiency#
The concept of token efficiency in large language models (LLMs) is crucial for optimizing both computational resources and inference speed. The paper explores this by introducing a hybrid representation of reasoning processes, leveraging latent discrete tokens alongside traditional text tokens. This approach significantly reduces the length of reasoning traces, leading to improved token efficiency. The reduction in trace length is achieved by abstracting away initial reasoning steps using a vector-quantized variational autoencoder (VQ-VAE), thereby compressing the information into fewer tokens. The effectiveness of this method is demonstrated across various benchmarks, showing consistent improvements in reasoning tasks while using significantly shorter input sequences. The method also incorporates a randomized replacement strategy during training, enabling fast adaptation to new latent tokens, further enhancing token efficiency and overall performance. Reduced computational cost and faster inference are the direct benefits of this improved token efficiency, making the approach particularly valuable for resource-constrained environments and applications requiring real-time responses.
More visual insights#
More on figures

🔼 The figure illustrates the Vector Quantized Variational Autoencoder (VQ-VAE) used to generate latent tokens for compressing reasoning traces. The VQ-VAE consists of an encoder (f_enc), a codebook, a quantizer (q), and a decoder (f_dec). The encoder maps sequences of text tokens representing reasoning steps into continuous embedding vectors. These vectors are then quantized to the nearest codebook entry using the quantizer, yielding a discrete latent token representing the original sequence. The decoder maps these latent tokens back to text tokens. This process converts the original sequence of text tokens into a compressed sequence of discrete latent tokens, which can be used to shorten reasoning traces and improve efficiency. The VQ-VAE is trained on the whole input sequence X to enhance the quality of latent abstractions, although it only operates on the reasoning steps during inference, effectively abstracting away the less informative initial steps of the reasoning process.
read the caption
Figure 3.2: A graphical illustration of our VQ-VAE. fencsubscript𝑓enc{f_{\text{enc}}}italic_f start_POSTSUBSCRIPT enc end_POSTSUBSCRIPT encodes the text tokens into latent embeddings, which are quantized by checking the nearest neighbors in the codebook. fdecsubscript𝑓dec{f_{\text{dec}}}italic_f start_POSTSUBSCRIPT dec end_POSTSUBSCRIPT decodes those quantized embeddings back to text tokens. When applying the VQ-VAE to compress the text tokens, the discrete latent tokens Z𝑍Zitalic_Z are essentially the index of corresponding embeddings in the codebook.

🔼 This figure shows a comparison of the average attention weights across input prompt tokens between the proposed latent model and the baseline CoT model for the question: What is the positive difference between 120% of 30 and 130% of 20?. The latent model demonstrates a stronger focus on numerical values and mathematical operation tokens, highlighting its improved ability to process mathematical problems.
read the caption
(a) Prompt: What is the positive difference between $120%$ of 30 and $130%$ of 20?

🔼 This figure shows the attention weights visualization for the second question in the prompt: Mark has $50 in his bank account; he earns $10 per day at his work. If he wants to buy a bike that costs $300, how many days does Mark have to save his money?. The visualization compares the attention weights of the model using the proposed latent approach against the baseline CoT model. It demonstrates that the latent approach focuses more attention on the numbers (50, 10, 300) and words representing mathematical operations, indicating a better understanding of the problem’s numerical aspects.
read the caption
(b) Prompt: Mark has $50 in his bank account. He earns $10 per day at his work. If he wants to buy a bike that costs $300, how many days does Mark have to save his money?

🔼 Figure 4.1 presents a comparison of attention weights between the proposed latent approach and the baseline chain-of-thought (CoT) method. The visualization shows the average attention weights assigned to input tokens during the generation of responses for two mathematical reasoning problems. The latent model is shown to have significantly higher attention weights on numbers and operation-related tokens compared to the CoT model, indicating a stronger focus on core numerical computation in the latent approach.
read the caption
Figure 4.1: Comparing with the CoT model, our latent approach have high attention weights on numbers and text tokens representing mathematical operations.
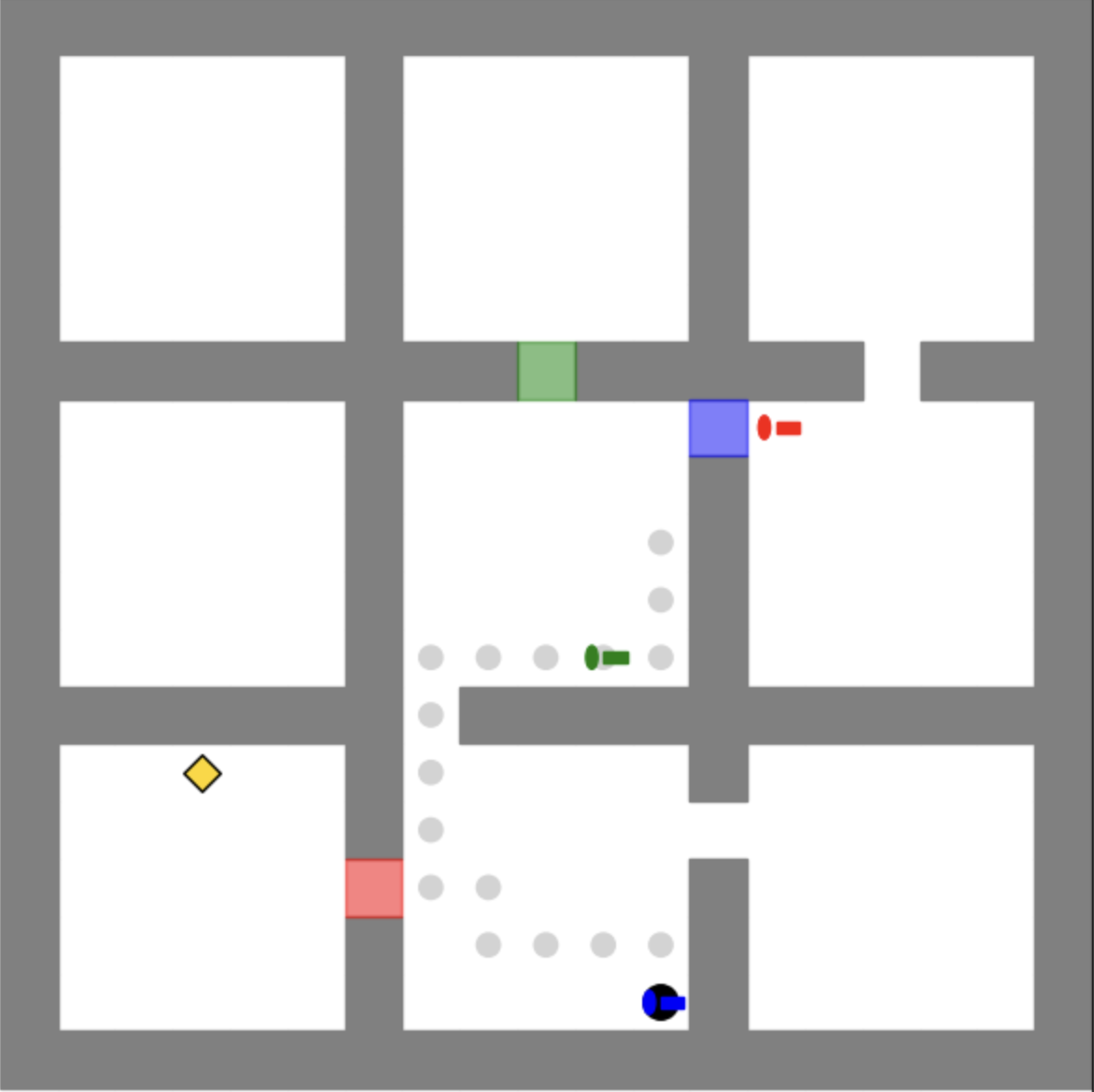
🔼 This figure shows a visual representation of the Keys-Finding Maze environment used in the experiments. It’s a grid-based maze where an agent needs to navigate to a target location by collecting keys to open color-coded doors. The maze is composed of multiple interconnected rooms, making it more complex than a simple path-finding problem.
read the caption
Figure A.1: An example of the keys-finding maze environment.

🔼 This figure shows the first phase of a multi-step process in a Keys-Finding Maze environment. The agent (black circle) is in a maze and must navigate to a goal location (gold diamond). To get there, they must collect keys of different colors (red, green, blue) that correspond to similarly colored doors, one key at a time. This first phase depicts the agent’s initial state and the location of the goal, keys and doors.
read the caption
(a) Phase 1

🔼 This phase of the Keys-Finding Maze shows the agent, after obtaining the blue key in Phase 1, proceeding to open the blue door to access the red key. The agent’s next step will involve using the red key.
read the caption
(b) Phase 2

🔼 This figure shows the third phase of an agent’s optimal trajectory in a keys-finding maze. The agent has already acquired the blue key, opened the blue door, and obtained the red key. In this phase, the agent is moving towards the red door to use the red key to open it.
read the caption
(c) Phase 3
More on tables
| Parameter | Value |
|---|---|
| Number of Layers (Transformer Blocks) | 12 |
| Hidden Size (Embedding Size) | 768 |
| Number of Attention Heads | 12 |
| Vocabulary Size | 50,257 |
| Total Number of Parameters | 117 million |
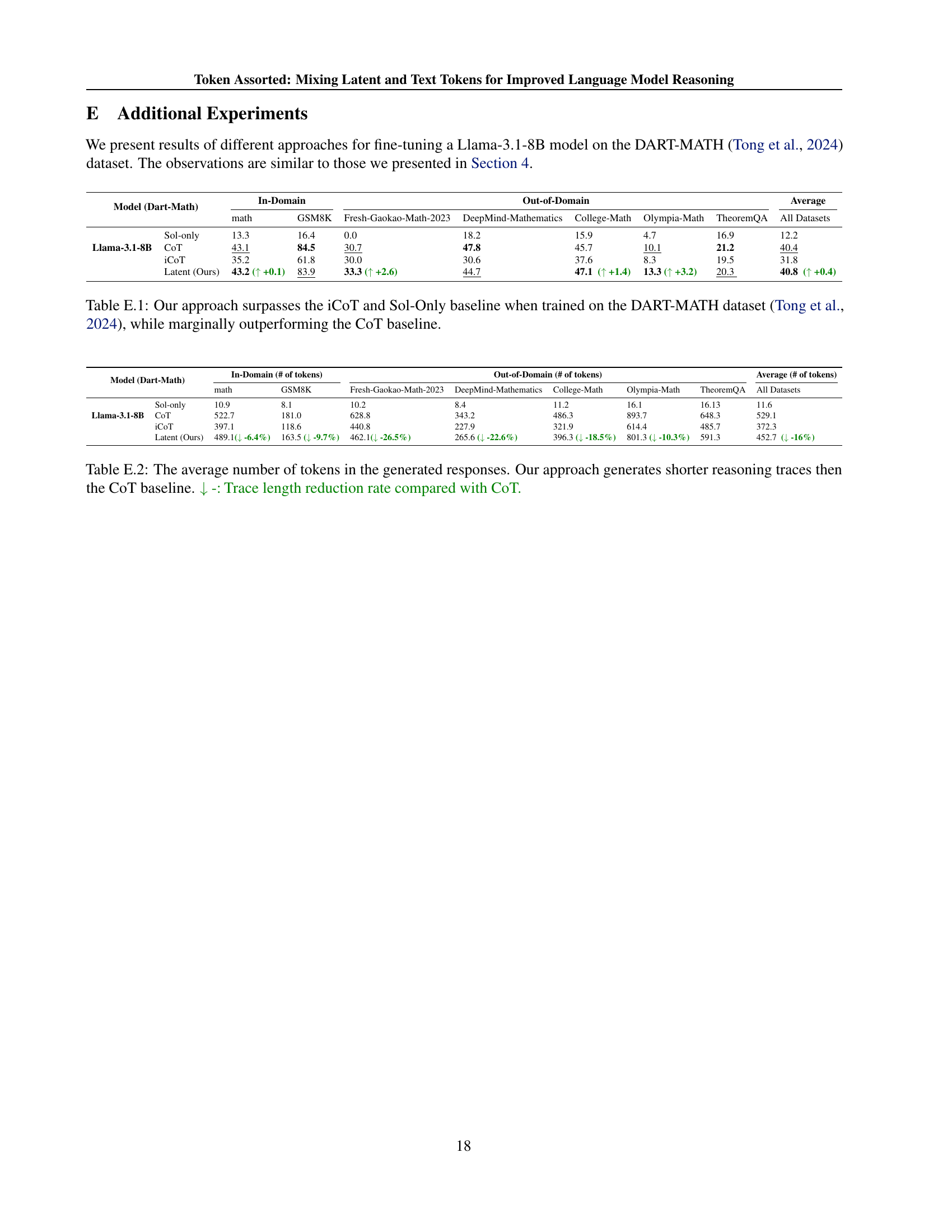
🔼 Table 4.2 presents a comprehensive evaluation of the proposed ’latent approach’ on various mathematical reasoning benchmarks. Models were fine-tuned using the MetaMathQA dataset. The results are compared against several baselines: Sol-Only (trained only on solutions), CoT (trained with complete chain-of-thought), iCoT (iterative chain-of-thought elimination), and Pause Token (uses pause tokens). The table highlights performance gains of the latent approach compared to the second-best baseline for each benchmark, categorized by in-domain (Math and GSM8K, which were used to create the MetaMathQA training data) and out-of-domain datasets. Bold text indicates the best result, underlined text the second-best, and the arrows indicate the performance improvements.
read the caption
Table 4.2: Our latent approach outperforms the baselines on various types of mathematical reasoning benchmarks. The models are fine-tuned on the MetaMathQA (Yu et al., 2023) dataset. The Math and GSM8K are in-domain datasets since they are used to generate MetaMathQA, while the others are out-of-domain. Bold: best results. Underscore: second best results. ↑↑\uparrow↑ +: Performance gain compared with the second best result.
| input text sample where means concatenation | |
| prompt of length | |
| the -th token of prompt (in text) | |
| reasoning trace of length | |
| the -th token of trace (in text) | |
| solution of length | |
| the -th token of solution (in text) | |
| the complete latent reasoning traces of length | |
| the -th token of latent trace | |
| compression rate | |
| number of trace tokens to be replaced by latent tokens during training | |
| modified input with mixed text and latent tokens | |
| codebook of VQ-VAE | |
| the -th vector in the codebook, which corresponds to the -th latent token | |
| dimension of s | |
| vocabulary of text tokens | |
| chunk size | |
| encodes a chunk of text tokens to embedding vectors | |
| embedding vectors of outputted by | |
| quantization operator that replaces, e.g., by its nearest neighbor in : | |
| maps prompt to a -dimensional embedding vector | |
| decodes quantized embedding vectors in back to text tokens, | |
| conditioning on prompt embedding generated by |
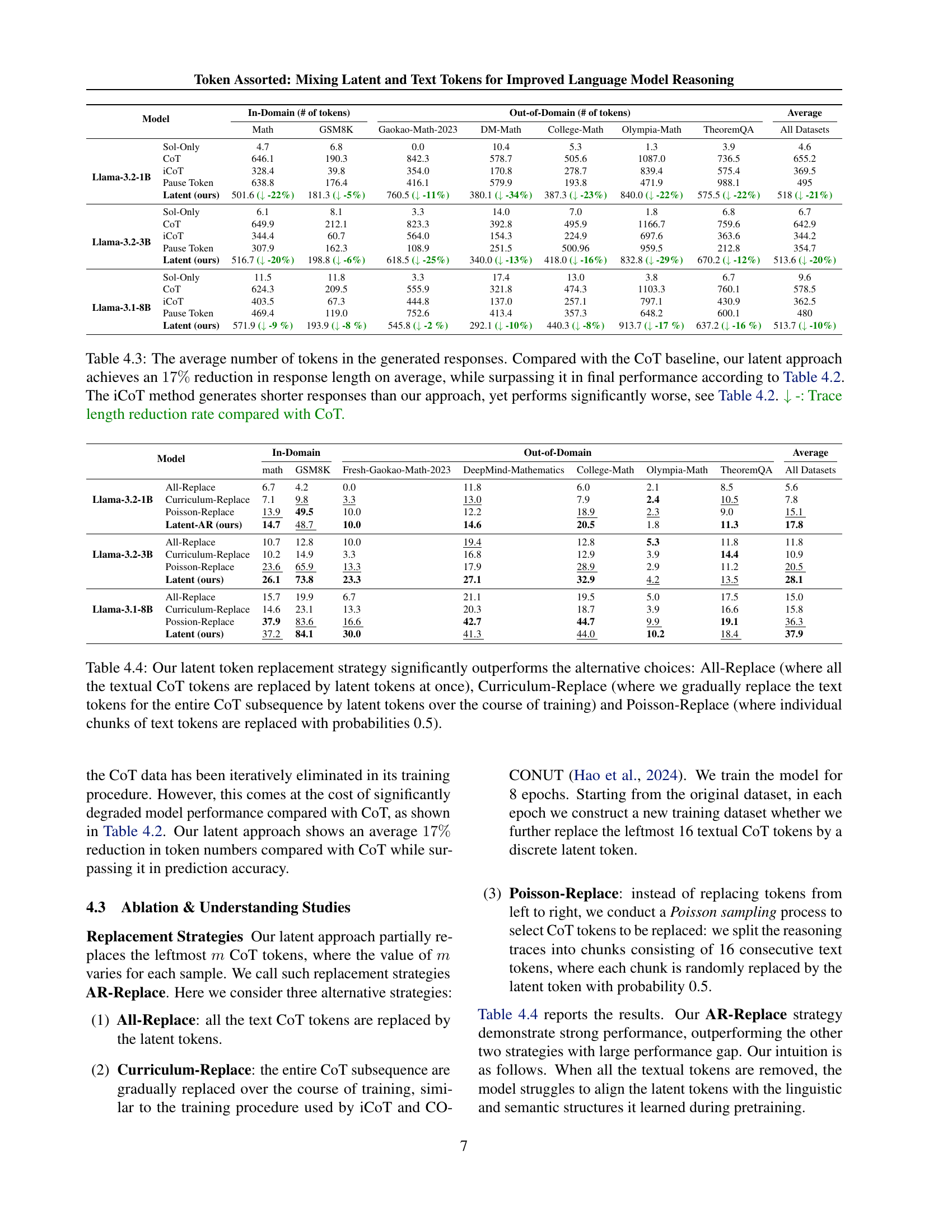
🔼 Table 4.3 presents a detailed comparison of the average number of tokens used in generated responses across different methods. It shows that the proposed ’latent’ approach significantly reduces the response length (by 17%) compared to the standard Chain-of-Thought (CoT) method, while simultaneously achieving superior performance (as shown in Table 4.2). The table also demonstrates that while the iCoT method generates even shorter responses, its overall accuracy is substantially lower than the latent approach. The percentage reduction in response length compared to CoT is also indicated for each method.
read the caption
Table 4.3: The average number of tokens in the generated responses. Compared with the CoT baseline, our latent approach achieves an 17%percent1717\%17 % reduction in response length on average, while surpassing it in final performance according to Table 4.2. The iCoT method generates shorter responses than our approach, yet performs significantly worse, see Table 4.2. ↓↓\downarrow↓ -: Trace length reduction rate compared with CoT.
Full paper#