TL;DR#
Current research largely assumes that complex reasoning in large language models (LLMs) necessitates enormous training datasets, often exceeding 100,000 examples. This data-intensive approach is computationally expensive and resource-demanding, posing significant challenges for researchers. Moreover, the prevailing belief is that supervised fine-tuning primarily leads to memorization rather than true generalization, limiting the broad applicability of these models.
The paper introduces LIMO, a novel approach that challenges these assumptions. LIMO demonstrates that complex mathematical reasoning can be effectively achieved using a surprisingly small number of carefully curated training samples (only 817). This significantly reduces the need for massive datasets and computational resources. Furthermore, LIMO’s success extends beyond in-domain tasks; it exhibits exceptional out-of-distribution generalization capabilities, outperforming models trained on significantly larger datasets. The researchers attribute this success to a synergistic combination of rich pre-trained knowledge and efficient computational strategies during inference, which they term the ‘Less-is-More’ hypothesis.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the common assumption that complex reasoning in LLMs requires massive datasets. Its findings on data efficiency have significant implications for model training and resource optimization, opening exciting avenues for future research in data-efficient AI.
Visual Insights#

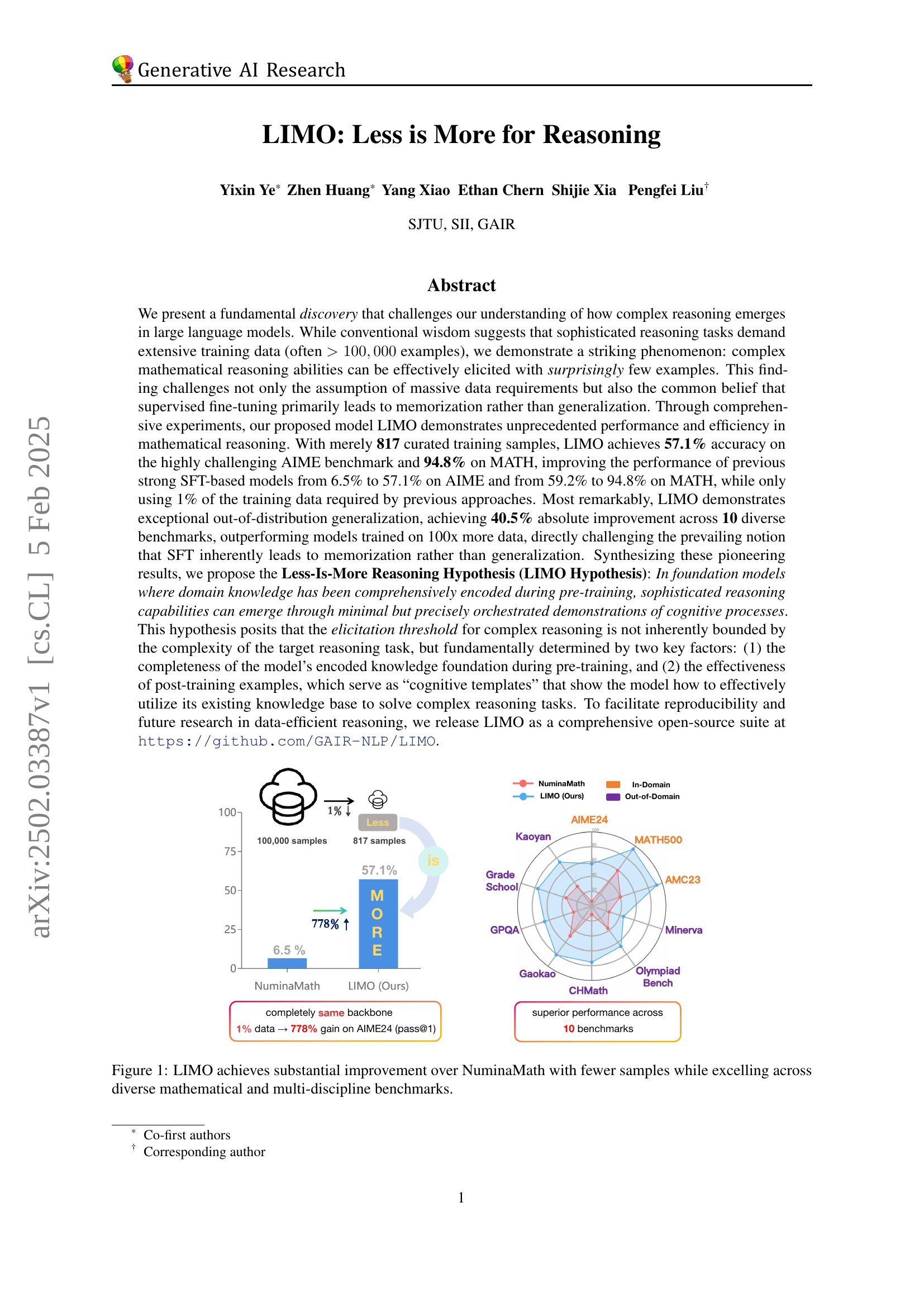
🔼 This figure showcases the performance of the LIMO model compared to NuminaMath. LIMO demonstrates significantly better performance across various mathematical and multi-disciplinary benchmarks, achieving this with a drastically smaller number of training samples (817 samples for LIMO vs. 100,000 for NuminaMath). The chart visually represents LIMO’s superior performance across multiple evaluation metrics, highlighting its efficiency and effectiveness even with limited data. The results suggest that LIMO’s superior performance is due to its capability to effectively utilize a pre-trained knowledge base, thus reducing the need for extensive supervised fine-tuning.
read the caption
Figure 1: LIMO achieves substantial improvement over NuminaMath with fewer samples while excelling across diverse mathematical and multi-discipline benchmarks.
| Aspect | General Alignment (LIMA) | Complex Reasoning (LIMO) |
| Core Capability | Response format and style adaptation for general-purpose interaction | Multi-step logical inference and complex cognitive reasoning |
| Knowledge Foundation | • General text corpus sufficient • Social interaction patterns • Basic world knowledge | • Diverse reasoning paradigms and problem-solving approaches • Rich context for exploring alternative solutions • Deep conceptual connections across domains |
| Computation Requirements | • Fixed-length generation sufficient • Single-pass processing adequate • Limited context window acceptable | • Scalable inference-time computation essential • Extended reasoning chain support required • Large cognitive workspace necessary |
| Historical Prerequisites | Emerged in 2023, requiring only: • Base models with general knowledge • Basic prompt engineering techniques | Emerged in 2025, requiring convergence of: • Advanced reasoning architectures • Inference-time scaling revolution |
| Training Data Quality | • Question Design: – Common interaction scenarios – Standard task diversity – Basic instruction following • Solution Quality: – Clear communication style – Format consistency – Appropriate tone | • Question Design: – High-difficulty problems fostering complex reasoning – Problems deviating from training distribution – Cross-domain knowledge integration challenges • Solution Quality: – Optimal structure with adaptive step granularity – Strategic cognitive scaffolding for reasoning – Rigorous verification throughout solution |
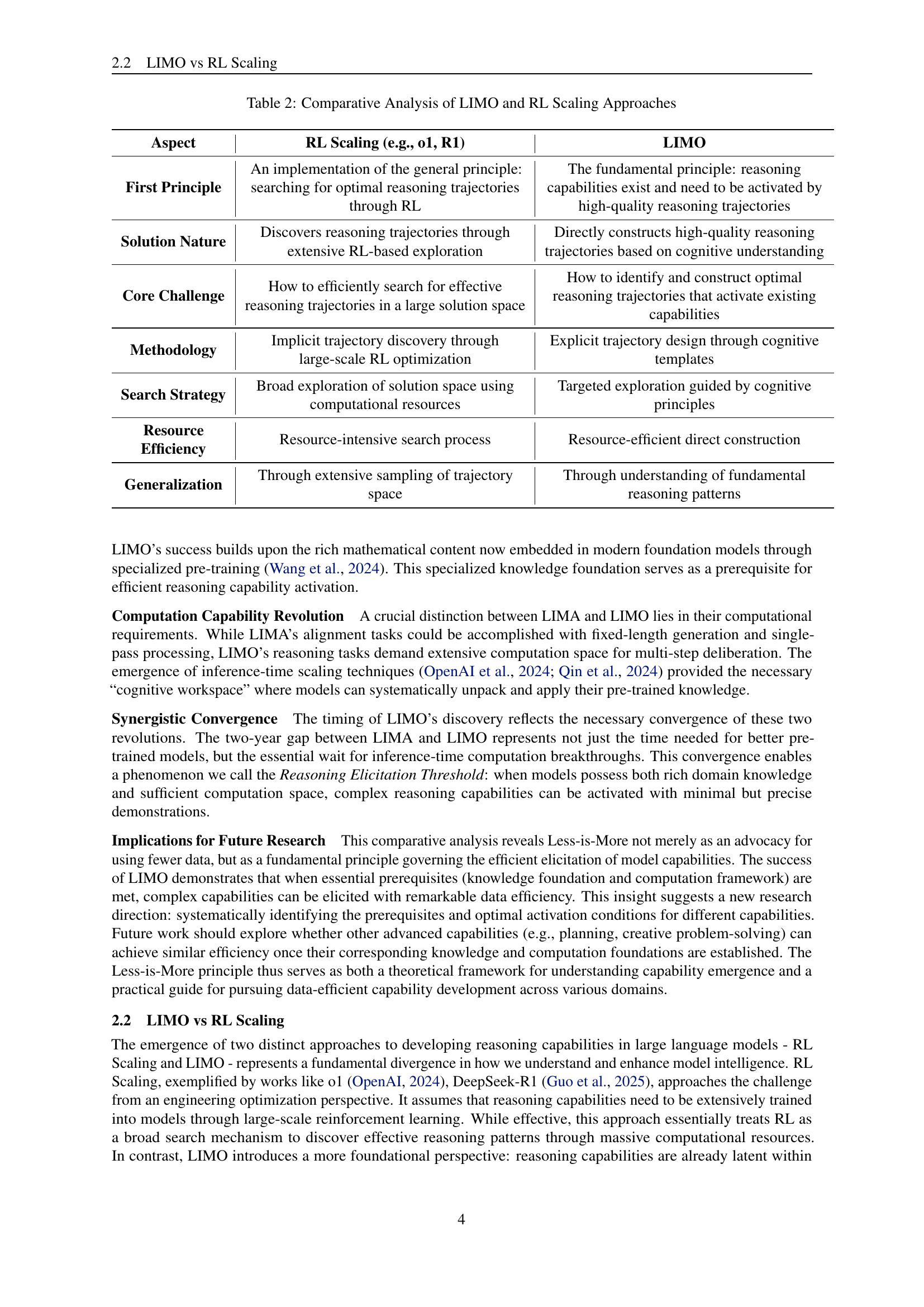
🔼 This table compares and contrasts two different paradigms in training large language models (LLMs): general alignment (represented by LIMA) and complex reasoning (represented by LIMO). It highlights key differences in their core capabilities, knowledge foundations, computational requirements, historical prerequisites, and training data quality. This comparison helps illustrate how the ‘Less-is-More’ phenomenon, initially observed in general alignment, extends to the more challenging domain of complex reasoning. The table details how LIMO leverages pre-trained knowledge and efficient inference-time computation to achieve sophisticated reasoning with significantly less training data than previously thought necessary.
read the caption
Table 1: Comparative Analysis: Less-is-More Phenomena in Language Models
In-depth insights#
LIMO Hypothesis#
The Less-Is-More Reasoning (LIMO) Hypothesis posits that complex reasoning capabilities in large language models (LLMs) can emerge from minimal, precisely structured training data. This challenges the prevailing belief that massive datasets are necessary for sophisticated reasoning. The hypothesis hinges on two crucial factors: a comprehensive knowledge foundation encoded during pre-training and the effectiveness of post-training examples serving as cognitive templates. The carefully selected examples aren’t about sheer quantity but about demonstrating cognitive processes and allowing the model to utilize its pre-existing knowledge base effectively. LIMO’s success is a testament to this data efficiency: achieving impressive results on complex mathematical reasoning tasks using only a fraction of the data employed by previous methods. This paradigm shift suggests that focusing on the quality and strategic design of training examples, rather than quantity, may unlock the full potential of LLMs for advanced reasoning.
Data-Efficient Reasoning#
The concept of data-efficient reasoning in large language models (LLMs) challenges the conventional wisdom that complex reasoning necessitates massive datasets. This paradigm shift suggests that sophisticated reasoning capabilities, particularly in mathematics, can be unlocked not through extensive training but by carefully curated, smaller datasets that effectively elicit the model’s pre-existing knowledge and guide its reasoning processes. The success of methods like LIMO hinges on a synergy between the richness of pre-trained knowledge and the efficacy of minimal, precisely-designed examples. These examples act as ‘cognitive templates,’ demonstrating effective cognitive processes, thereby unlocking latent reasoning potential rather than simply memorizing patterns. This approach offers significant advantages, reducing computational costs and data requirements, and promising a more efficient pathway toward achieving advanced AI capabilities. Future research should focus on identifying general principles of data-efficient reasoning applicable across domains and developing theoretical frameworks that explain this emergent phenomenon.
Cognitive Templates#
The concept of “cognitive templates” in the context of large language models (LLMs) is intriguing. It suggests that a small number of carefully chosen examples, acting as prototypical problem-solving demonstrations, can unlock complex reasoning abilities within an LLM. These templates don’t simply provide the model with answers, but rather showcase the cognitive processes involved. By observing how these templates leverage the model’s existing knowledge base, the LLM can generalize these strategies to novel problems. The effectiveness hinges on the richness of the LLM’s pre-trained knowledge, ensuring that the necessary components for reasoning are already present. Essentially, the cognitive template acts as a key, unlocking latent potential within a pre-trained model, rather than teaching new knowledge. This contrasts sharply with traditional fine-tuning approaches which rely on massive datasets. The crucial aspect lies in the design of the templates, ensuring they are both minimal and effectively illustrate the cognitive processes needed for sophisticated reasoning.
Benchmark Analyses#
Benchmark analyses in this research paper would ideally involve a multi-faceted approach. First, it’s crucial to select a diverse set of established benchmarks, encompassing both in-domain (mathematical reasoning) and out-of-domain (general reasoning and other disciplines) tasks to thoroughly evaluate the model’s generalization capabilities. Within each domain, benchmarks should vary in complexity, reflecting different levels of reasoning and problem-solving demands. Next, the methodology for evaluating model performance on these benchmarks must be clearly defined. This includes specifying evaluation metrics (e.g., accuracy, F1-score, BLEU score, etc.), and data analysis procedures. Careful attention should be given to handling potential biases and ensuring fair comparisons across different benchmarks and models. Finally, a thorough analysis of the results is needed, not merely reporting performance numbers but also interpreting the findings in the context of the LIMO hypothesis and related research. By carefully studying performance variations across benchmarks, valuable insights into the model’s strengths, weaknesses, and the general applicability of LIMO’s principles can be gained. A strong emphasis on qualitative analysis of model outputs, going beyond just quantitative results, is essential for gaining a deeper understanding of the model’s reasoning processes.
Future Research#
The “Future Research” section of this paper suggests several promising avenues. Domain generalization is crucial; extending the Less-is-More (LIMO) hypothesis beyond mathematical reasoning to scientific reasoning, logic, and causal inference is a key next step. This requires adapting quality metrics and developing domain-specific evaluation frameworks. Theoretical foundations need strengthening; a deeper understanding of the relationship between pre-training knowledge, inference-time computation, and reasoning capabilities is needed. This may involve finding the minimum pre-training knowledge threshold for effective reasoning and developing mathematical models to balance reasoning chain quality and quantity. Developing automated quality assessment tools is vital, moving beyond the current manual approach, to allow for scaling. Finally, exploring multi-modal integration is important; real-world reasoning often involves multiple modalities, so investigating how visual and structured data enhance mathematical reasoning is key, requiring new quality metrics for multi-modal chains and understanding information integration in reasoning. The overall goal is to move beyond empirical findings towards a more comprehensive theoretical understanding of data-efficient reasoning and its applicability to various domains.
More visual insights#
More on figures

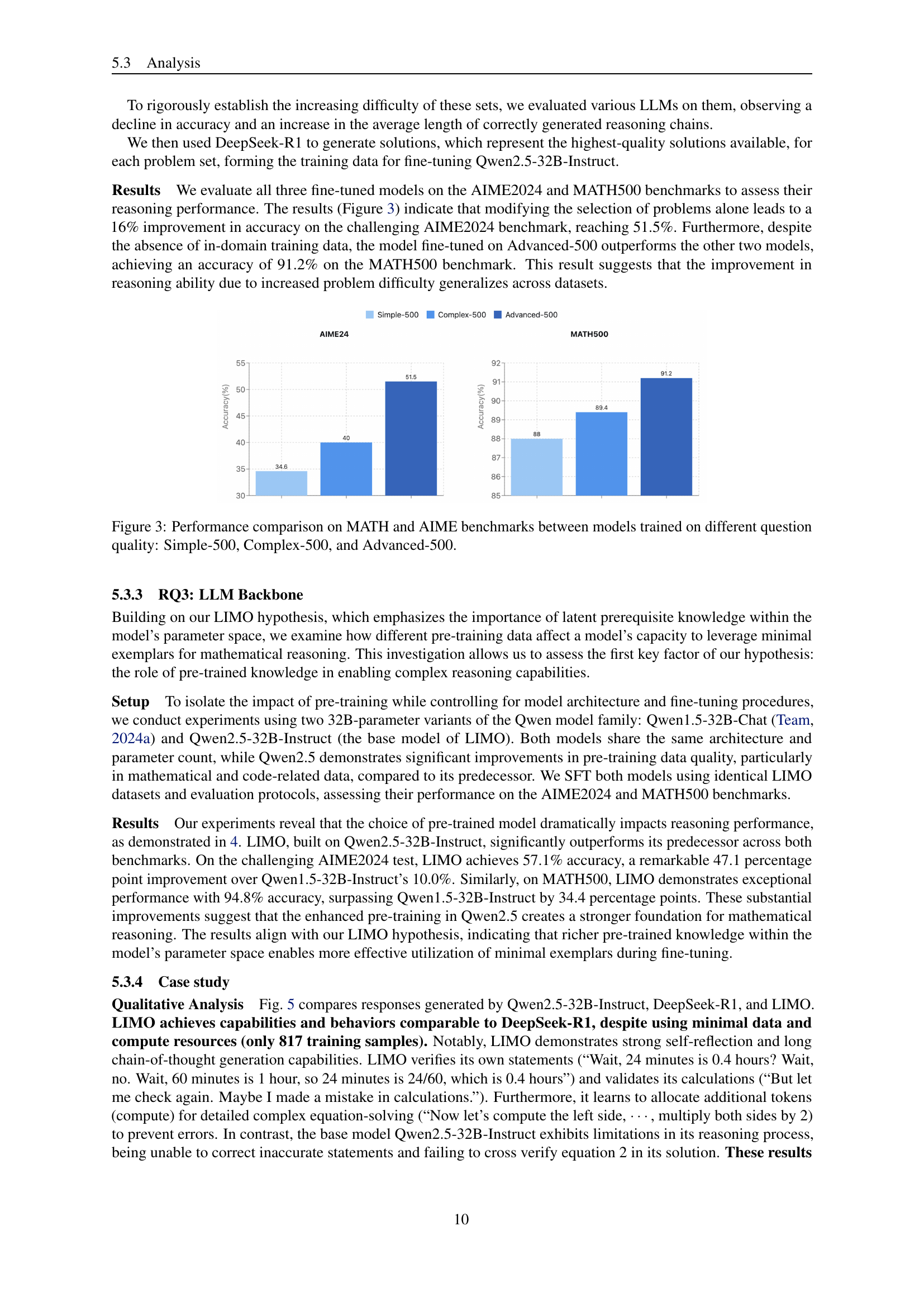
🔼 The figure shows the performance of models trained on reasoning chains of varying quality levels on two mathematical reasoning benchmarks: AIME24 and MATH500. The x-axis represents the five quality levels of reasoning chains (L1-L5, with L5 being the highest quality). The y-axis represents the accuracy of the model on each benchmark. The graph shows that models trained on higher quality reasoning chains (L4 and L5) consistently achieve significantly better performance compared to models trained on lower quality reasoning chains (L1, L2 and L3). The difference in performance highlights the substantial impact of reasoning chain quality on the model’s ability to solve mathematical reasoning problems. This supports the paper’s central hypothesis that high-quality, concise training data is more effective than large amounts of low-quality data in training strong reasoning capabilities in large language models.
read the caption
Figure 2: Comparison of models trained on reasoning chains of different quality levels.

🔼 Figure 3 presents a comparison of model performance on two mathematical reasoning benchmarks, MATH and AIME. Three different models were trained, each using a dataset of 500 problems of varying difficulty. Simple-500 represents a dataset of relatively easier problems, Complex-500 contains moderately difficult problems, and Advanced-500 consists of the most challenging problems. The figure displays the accuracy of each model on both benchmarks, illustrating the impact of question difficulty on model performance and showing that models trained on more challenging problems achieve higher accuracy.
read the caption
Figure 3: Performance comparison on MATH and AIME benchmarks between models trained on different question quality: Simple-500, Complex-500, and Advanced-500.

🔼 This figure compares the performance of two large language models (LLMs) fine-tuned using the same dataset (LIMO) but with different pre-trained backbones: Qwen1.5-32B-Chat and Qwen2.5-32B-Instruct. The models’ performance is evaluated on two mathematical reasoning benchmarks: the American Invitational Mathematics Examination (AIME24) and MATH500. The results demonstrate a significant improvement in performance when using Qwen2.5-32B-Instruct as the pre-trained model, highlighting the importance of the pre-trained model’s knowledge base in achieving high performance in mathematical reasoning tasks, even with minimal fine-tuning data. This supports the paper’s Less-Is-More Reasoning Hypothesis.
read the caption
Figure 4: Impact of Pre-trained Model Choice on Mathematical Reasoning Performance

🔼 Figure 5 showcases a comparative analysis of responses generated by three different large language models (LLMs) to the same mathematical reasoning problem. The models compared are Qwen2.5-32B-Instruct (a strong baseline model), DeepSeek-R1 (a model known for its advanced reasoning capabilities), and LIMO (the authors’ proposed model). The figure visually illustrates the differences in the approaches these models take to solving the problem, highlighting LIMO’s superior performance and ability to generate more detailed, self-correcting reasoning chains. This emphasizes LIMO’s enhanced reasoning capability and its ability to leverage the full inference-time compute capabilities, aspects directly related to the Less-is-More Reasoning Hypothesis presented in the paper.
read the caption
Figure 5: Comparison between the responses generated by Qwen2.5-32B-Instruct, DeepSeek-R1, and LIMO
More on tables
| Aspect | RL Scaling (e.g., o1, R1) | LIMO |
| First Principle | An implementation of the general principle: searching for optimal reasoning trajectories through RL | The fundamental principle: reasoning capabilities exist and need to be activated by high-quality reasoning trajectories |
| Solution Nature | Discovers reasoning trajectories through extensive RL-based exploration | Directly constructs high-quality reasoning trajectories based on cognitive understanding |
| Core Challenge | How to efficiently search for effective reasoning trajectories in a large solution space | How to identify and construct optimal reasoning trajectories that activate existing capabilities |
| Methodology | Implicit trajectory discovery through large-scale RL optimization | Explicit trajectory design through cognitive templates |
| Search Strategy | Broad exploration of solution space using computational resources | Targeted exploration guided by cognitive principles |
| Resource Efficiency | Resource-intensive search process | Resource-efficient direct construction |
| Generalization | Through extensive sampling of trajectory space | Through understanding of fundamental reasoning patterns |
🔼 This table compares and contrasts the Less-is-More Reasoning (LIMO) approach with Reinforcement Learning (RL) scaling methods for developing reasoning capabilities in large language models. It highlights the core principles, solution nature, key challenges, methodologies, search strategies, resource efficiency, and generalization characteristics of each approach, providing a detailed comparison of their philosophical underpinnings and practical implementations.
read the caption
Table 2: Comparative Analysis of LIMO and RL Scaling Approaches
| Datasets | OpenAI-o1 -preview | Qwen2.5-32B -Instruct | QwQ-32B- preview | OpenThoughts (114k) | NuminaMath (100k) | LIMO ours(817) |
| In Domain | ||||||
| AIME24 | 44.6 | 16.5 | 50.0 | 50.2 | 6.5 | 57.1 |
| MATH500 | 85.5 | 79.4 | 89.8 | 80.6 | 59.2 | 94.8 |
| AMC23 | 81.8 | 64.0 | 83.6 | 80.5 | 40.6 | 92.0 |
| Out of Domain | ||||||
| OlympiadBench | 52.1 | 45.3 | 58.5 | 56.3 | 36.7 | 66.8 |
| CHMath | 50.0 | 27.3 | 68.5 | 74.1 | 11.2 | 75.4 |
| Gaokao | 62.1 | 72.1 | 80.1 | 63.2 | 49.4 | 81.0 |
| Kaoyan | 51.5 | 48.2 | 70.3 | 54.7 | 32.7 | 73.4 |
| GradeSchool | 62.8 | 56.7 | 63.8 | 39.0 | 36.2 | 76.2 |
| Minerva | 47.1 | 41.2 | 39.0 | 41.1 | 24.6 | 44.9 |
| GPQA | 73.3 | 48.0 | 65.1 | 42.9 | 25.8 | 66.7 |
| AVG. | 61.1 | 49.9 | 66.9 | 58.3 | 32.3 | 72.8 |
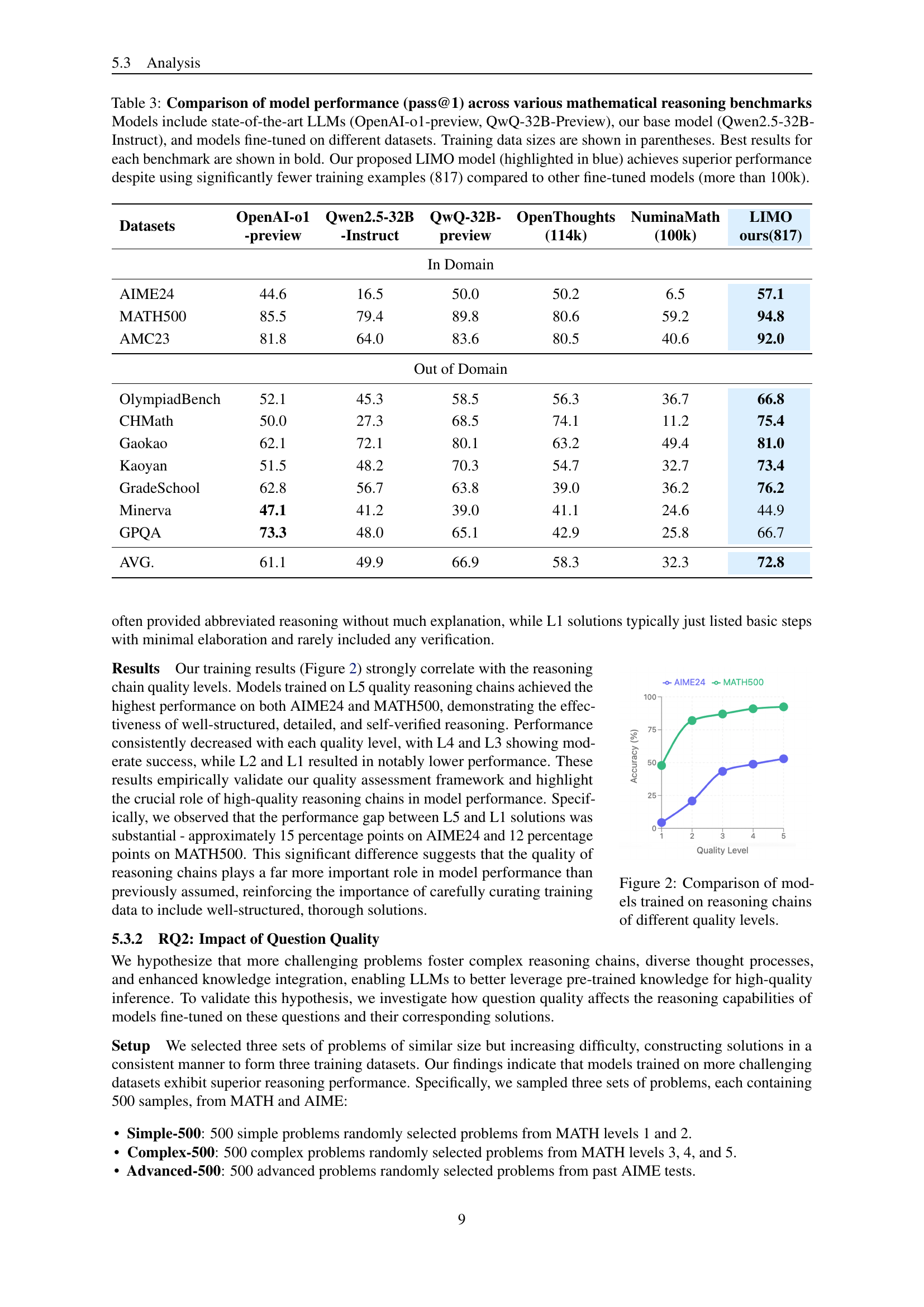
🔼 This table compares the performance of various large language models (LLMs) on several mathematical reasoning benchmarks. The models include state-of-the-art models like OpenAI-o1-preview and QwQ-32B-Preview, a base Qwen2.5-32B-Instruct model, and models fine-tuned using different datasets. The table shows the pass@1 accuracy (percentage of correctly answered questions in the first try) for each model on each benchmark. The number of training examples used for fine-tuning is indicated in parentheses. The best result for each benchmark is highlighted in bold. Notably, the LIMO model, highlighted in blue, significantly outperforms other models despite using only 817 training examples compared to over 100,000 for the others, demonstrating high data efficiency.
read the caption
Table 3: Comparison of model performance (pass@1) across various mathematical reasoning benchmarks Models include state-of-the-art LLMs (OpenAI-o1-preview, QwQ-32B-Preview), our base model (Qwen2.5-32B-Instruct), and models fine-tuned on different datasets. Training data sizes are shown in parentheses. Best results for each benchmark are shown in bold. Our proposed LIMO model (highlighted in blue) achieves superior performance despite using significantly fewer training examples (817) compared to other fine-tuned models (more than 100k).
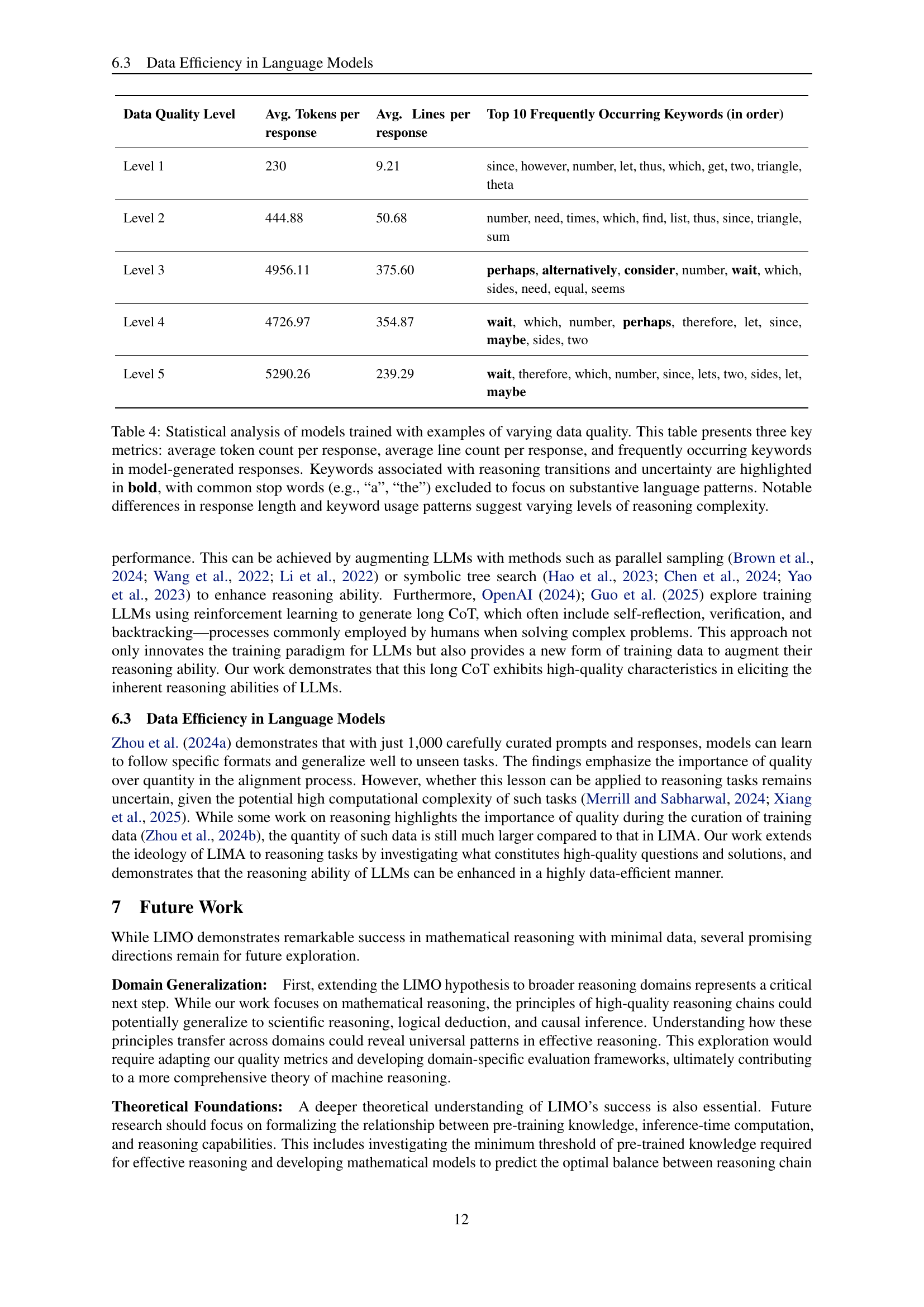
| Data Quality Level | Avg. Tokens per response | Avg. Lines per response | Top 10 Frequently Occurring Keywords (in order) |
| Level 1 | 230 | 9.21 | since, however, number, let, thus, which, get, two, triangle, theta |
| Level 2 | 444.88 | 50.68 | number, need, times, which, find, list, thus, since, triangle, sum |
| Level 3 | 4956.11 | 375.60 | perhaps, alternatively, consider, number, wait, which, sides, need, equal, seems |
| Level 4 | 4726.97 | 354.87 | wait, which, number, perhaps, therefore, let, since, maybe, sides, two |
| Level 5 | 5290.26 | 239.29 | wait, therefore, which, number, since, lets, two, sides, let, maybe |
🔼 Table 4 shows a statistical analysis comparing models trained on examples of varying quality. The analysis focuses on three key metrics: average token count per response, average line count per response, and the frequency of keywords in generated responses. Keywords indicative of reasoning transitions (e.g., indicating uncertainty or complex thought processes) are highlighted in bold. Common words like ‘a’ and ’the’ were excluded to focus on the substantive word usage. Significant differences in response length and the type of keywords used suggest a correlation between training data quality and reasoning complexity. Higher quality training data leads to longer responses with more sophisticated vocabulary related to complex reasoning processes.
read the caption
Table 4: Statistical analysis of models trained with examples of varying data quality. This table presents three key metrics: average token count per response, average line count per response, and frequently occurring keywords in model-generated responses. Keywords associated with reasoning transitions and uncertainty are highlighted in bold, with common stop words (e.g., “a”, “the”) excluded to focus on substantive language patterns. Notable differences in response length and keyword usage patterns suggest varying levels of reasoning complexity.
Full paper#