Teaching Language Models to Critique via Reinforcement Learning

2502.03492

Zhihui Xie et el.

🤗 2025-02-12

TL;DR
#

Large language models (LLMs) are rapidly advancing, but their potential for self-improvement is hindered by the difficulty of providing accurate and actionable feedback. Existing methods, including reward models and automated verification, often fall short. This limits the progress towards building truly autonomous AI systems that can iteratively refine their outputs.

The paper proposes CTRL (Critic Training via Reinforcement Learning), a novel framework that addresses these challenges. CTRL trains a specialized critic model to generate feedback that guides the generator model towards better solutions. This is achieved through a two-stage process combining supervised fine-tuning with reinforcement learning. The results show significant performance gains across various code generation benchmarks and illustrate the method’s effectiveness in test-time scaling via iterative critique-revision. This decoupled approach demonstrates strong generalization capabilities and offers a promising path towards building more robust self-improving AI systems.

Key Takeaways
#

Why does it matter?
#

This paper is crucial because it introduces a novel framework for training language models to provide effective critique, addressing a major challenge in autonomous AI system development. It offers a new perspective on self-improvement in LLMs, moves beyond limitations of existing methods, and opens avenues for more robust and reliable AI systems. The work’s findings have significant implications for building more autonomous AI systems and its methodology is easily adaptable to other domains.

Visual Insights
#

🔼 This figure showcases the performance improvement achieved by iterative critique-revision using the proposed CTRL framework. Two graphs are shown: one demonstrates the performance of the CTRL critic (finetuned on Qwen2.5-Coder-32B-Ins) when paired with the Qwen2.5-Coder generator, and the other shows the results when paired with a stronger GPT-40 generator. The x-axis represents the number of critique-revision iterations, and the y-axis represents the pass rate (Pass@1). The figure highlights the significant performance scaling of CTRL across multiple iterations and different generator models. The shaded regions illustrate the standard error calculated across five independent trials.
read the caption
Figure 1: Performance scaling of our CTRL critic (finetuned on Qwen2.5-Coder-32B-Ins, henceforth Qwen2.5-Coder) compared to other critics across different generators on CodeContests. CTRL demonstrates strong critiquing capabilities not only when paired with its base model but also with a stronger generator (GPT-4o, right). Shaded regions indicate standard error across 5 seeds.

	Pass@1	$\Delta_{\uparrow}$	$\Delta_{\downarrow}$
Zero-shot	7.88	0.00	0.00
Execution Feedback (EF)^†	8.97	2.42	1.33
Self-critique w/ EF^†	11.76	3.88	0.00
Self-critique	8.36	2.30	1.82
Critique w/ CTRL ${}_{\text{SFT}}$	8.36	3.52	3.03
Critique w/ CTRL	11.76	4.73	0.85
Critique $\times 2$ w/ CTRL	14.18	7.27	0.97
Critique $\times 3$ w/ CTRL	15.15	8.12	0.85

🔼 Table 1 presents the results of an experiment evaluating the effectiveness of different feedback mechanisms in improving the performance of a code generation model. The experiment used Qwen2.5-Coder as the code generation model and compared its zero-shot performance (without any feedback) against its performance with critique-revision using different feedback methods. The table shows the Pass@1 rate (the percentage of times the model generates a correct solution in one attempt) for each condition. Critique-revision involved iteratively refining the model’s output based on feedback, and the ‘×k’ notation indicates the number of critique-revision iterations performed (e.g., ×2 means two iterations). The † symbol indicates that unit tests were used during the generation process for that specific condition.
read the caption
Table 1: Critique-revision performance (Pass@1, %) on CodeContests. We fix the generator model to be Qwen2.5-Coder, and compare zer-shot performance with critique-revision performance using different feedback mechanisms. ×kabsent𝑘\times k× italic_k represents conducting iterative critique-revision k𝑘kitalic_k times. †using unit tests for generation.

In-depth insights
#

LLM Self-Critique
#

LLM self-critique explores the fascinating capability of large language models (LLMs) to evaluate their own outputs. This self-assessment is crucial for iterative improvement, enabling autonomous refinement without human intervention. Existing approaches often rely on reward models or external verification tools, which can be limiting. Reward models provide simplified feedback, lacking detailed suggestions for improvement, while verification tools offer low-level information not directly applicable to high-level fixes. Effective self-critique requires a fine balance: accurate evaluation combined with actionable, constructive feedback. The challenge lies in training LLMs to provide not just correctness judgments but also specific and meaningful guidance on how to correct errors. This requires careful design of the feedback mechanisms and potentially a two-stage training process. A first stage might focus on synthesizing high-quality critiques using execution feedback and a second stage on optimizing the critique using reinforcement learning techniques. The ultimate goal is to create self-improving LLMs capable of iterative refinement, leading to higher-quality outputs and reduced human intervention. This is a complex but potentially highly impactful area of research that holds significant promise for advancing the capabilities of LLMs.

CTRL Framework
#

The CTRL framework, as presented in the research paper, focuses on training a critic model for large language models (LLMs) using reinforcement learning. The core innovation lies in decoupling the critic model from the generator model, allowing for independent training and improved generalization. This approach addresses the limitations of self-critique methods, which often struggle to provide actionable feedback. CTRL leverages a two-stage training process: first, using execution feedback to generate high-quality critiques, then refining the critic using a group relative policy optimization (GRPO) method for enhanced stability and efficiency. The key advantage of CTRL is its ability to effectively drive the generator model towards better solutions through iterative critique-revision, demonstrating significant improvements over baseline methods across various benchmarks. The framework’s ability to generalize to different generators and tasks, mitigating compounding errors during multi-turn revisions, is a significant contribution. The success of CTRL highlights the importance of a dedicated critic model for LLM self-improvement and provides a scalable and robust approach to enhance the quality of generated outputs.

Iterative Refinement
#

Iterative refinement, a core concept in the paper, focuses on improving model outputs through repeated cycles of critique and revision. The process hinges on accurate and actionable feedback, moving beyond simple reward signals to provide specific, targeted suggestions for improvement. This iterative approach is crucial because single-step corrections are insufficient for complex tasks; compounding errors can arise if mistakes are not addressed early. The paper demonstrates that a well-trained critic model significantly enhances the effectiveness of iterative refinement, leading to substantially higher success rates and more efficient processes, reducing the number of revision steps. This iterative approach, coupled with the proposed framework, directly addresses the limitations of prior self-improvement methods, showing that decoupling the critic and generator models is key to achieving meaningful, scalable improvements in large language model performance.

GRPO Optimization
#

The concept of “GRPO Optimization,” likely referring to Group Relative Policy Optimization, addresses the high variance inherent in policy gradient methods for training large language models (LLMs). Standard policy gradients suffer from noisy estimates due to the vastness of the action (critique) and state (solution) spaces. GRPO mitigates this by focusing on relative advantages within groups of critiques. Instead of directly estimating the absolute value of each critique, GRPO compares the performance of critiques within the same group. This relative approach reduces variance and improves the stability of the training process, allowing for more reliable learning of effective critique strategies. The key benefit is the improved signal-to-noise ratio, leading to more efficient and stable training of the critic model. The method’s effectiveness stems from its ability to prioritize learning from problems where critique quality makes a tangible difference, effectively avoiding wasteful computations on overly easy or difficult problems. This nuanced approach is crucial for maximizing the impact of the critic model in improving the quality of the generator model’s output.

Future Directions
#

Future research could explore several promising avenues. Improving the efficiency of the critique-revision process is crucial; current methods, while effective, can be computationally expensive. This might involve developing more efficient critic models or refining the iterative refinement strategy to minimize unnecessary revisions. Another area of focus should be on enhancing the generalizability of the critic models. The current models demonstrate strong performance on code generation tasks, but further investigation is needed to assess their applicability across other domains. Developing a more nuanced understanding of the interaction between critic and generator models is also vital. The current framework relies on a relatively simple interaction process, and exploring more complex feedback mechanisms could significantly improve performance. Finally, investigating the impact of different model architectures and training methodologies on critic effectiveness will lead to more robust and efficient critique generation. Research should also examine the ethical considerations surrounding the deployment of such powerful self-improving AI systems. Ensuring fairness, accountability, and transparency in these systems is critical.

More visual insights
#

More on figures

🔼 This figure illustrates the iterative process of code improvement using the proposed CTRL framework. The top panel shows an initial solution to a coding problem that utilizes a min-heap data structure. However, the critic identifies two crucial flaws: incorrect access of heap elements and inefficient query handling. The bottom panel depicts the critic’s feedback, which pinpoints these issues and suggests specific improvements. The improved solution, shown in the bottom panel, uses a max-heap and effectively addresses the identified problems. This example highlights the effectiveness of CTRL in providing actionable feedback that leads to significant improvements in code quality, showcasing its ability to guide a model toward correct code generation. This is taken from critiques of CTRL on LiveCodeBench.
read the caption
Figure 2: Illustration of the critique-correction process for a coding problem. Top: An initial solution is proposed by the task-performing using a min-heap approach. Bottom: The critic identifies flaws in the implementation (incorrect heap access and inefficient query handling) and suggests specific improvements, leading to a corrected max-heap solution. This example is taken from critiques of CTRL on LiveCodeBench, which demonstrates how structured feedback from the critic can guide meaningful improvements in code generation.

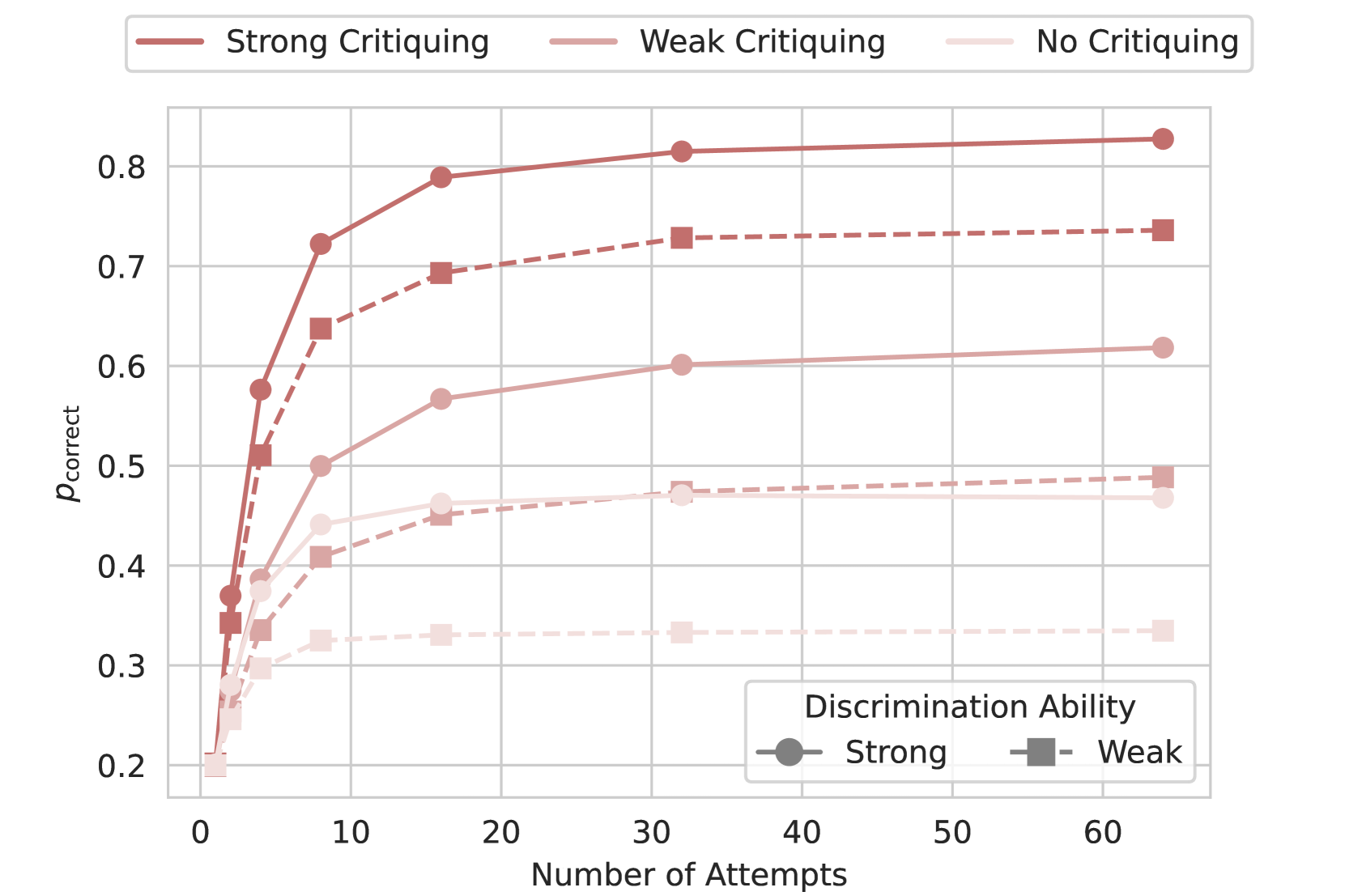
🔼 This figure displays the results of simulations comparing the effectiveness of different levels of critiquing and discrimination abilities in an iterative improvement process. The success probability (pcorrect) is plotted against the number of attempts. Three critiquing scenarios are examined: no critiquing (representing independent sampling of solutions), weak critiquing, and strong critiquing, each with varying levels of discrimination ability. The simulations demonstrate that strong critiquing abilities significantly improve success rates compared to no critiquing, even with weak discrimination.
read the caption
Figure 3: Simulation results showing success probability (pcorrectsubscript𝑝correctp_{\text{correct}}italic_p start_POSTSUBSCRIPT correct end_POSTSUBSCRIPT) as a function of the number of attempts, comparing different levels of critiquing and discrimination ability.

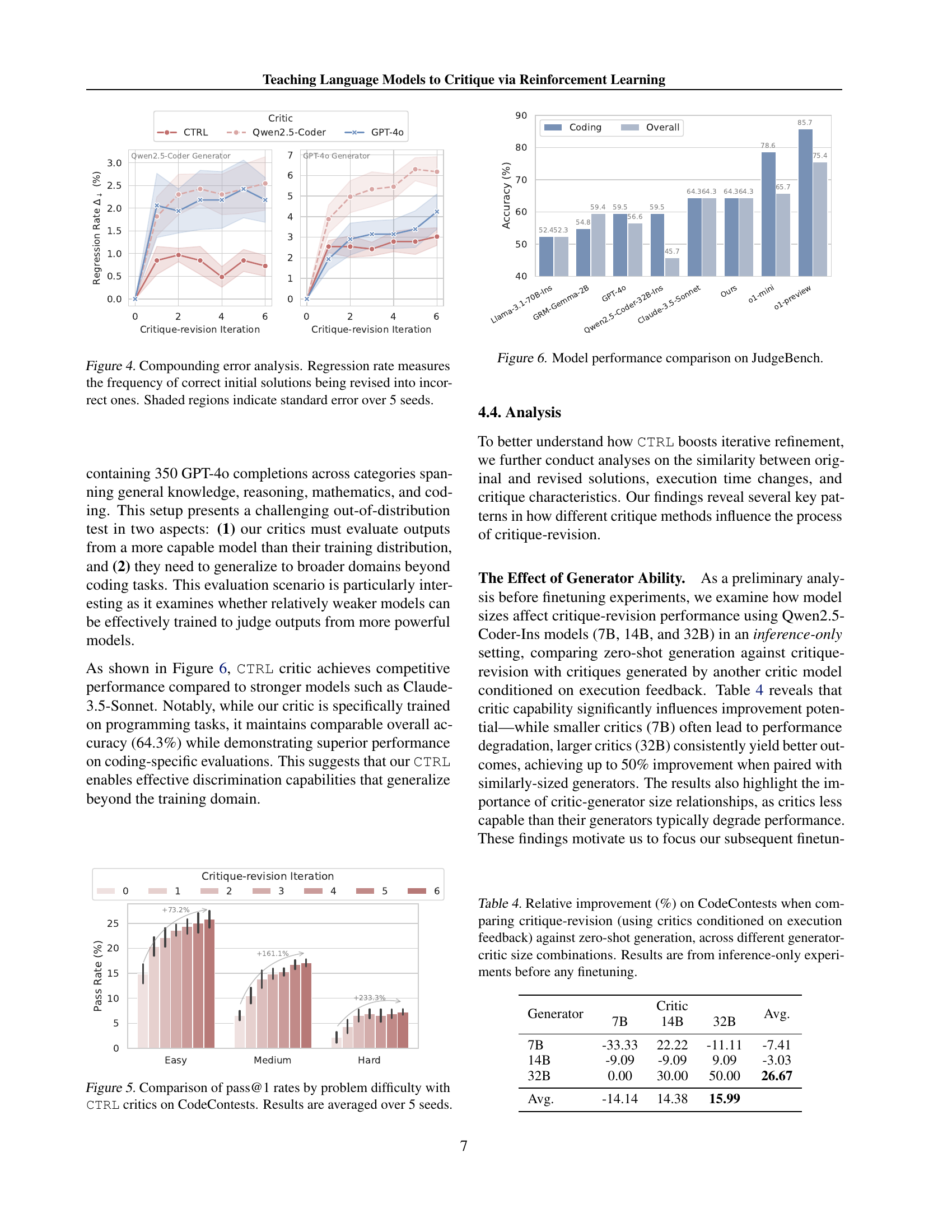
🔼 This figure analyzes the compounding error rate during iterative refinement. The regression rate shows how often initially correct solutions become incorrect after revisions. Two plots are shown, one for each of the two generator models, Qwen2.5-Coder and GPT-4, paired with the CTRL critic. The shaded areas represent the standard error calculated across five different random seeds, providing a measure of variability in the results.
read the caption
Figure 4: Compounding error analysis. Regression rate measures the frequency of correct initial solutions being revised into incorrect ones. Shaded regions indicate standard error over 5 seeds.

🔼 This figure shows the success rate (Pass@1) of the CTRL critic model on the CodeContests benchmark, categorized by problem difficulty levels (Easy, Medium, Hard). The results demonstrate how the effectiveness of the CTRL critic scales with problem complexity. Each data point represents the average Pass@1 rate across five independent runs of the experiment, showcasing the model’s robustness.
read the caption
Figure 5: Comparison of pass@1 rates by problem difficulty with CTRL critics on CodeContests. Results are averaged over 5 seeds.

🔼 The figure compares the performance of various large language models (LLMs) on the JudgeBench benchmark, which evaluates LLMs’ ability to discriminate between correct and incorrect outputs. The models compared include several strong LLMs and the CTRL critic. The x-axis shows different LLMs and the y-axis shows the accuracy of each model’s discrimination ability. The figure highlights the performance of the CTRL critic in relation to other, often stronger models.
read the caption
Figure 6: Model performance comparison on JudgeBench.

🔼 Figure 7 presents a comparison of code similarity between the original code and the revised code generated using two different methods on the CodeContests dataset. The left panel displays the distribution of similarity scores for both self-critique and the CTRL method. A lower similarity score suggests a more substantial change or revision of the code. The right panel provides a box plot visualization of these distributions, offering a clearer comparison of the central tendencies and spreads of similarity scores between the two methods.
read the caption
Figure 7: Comparison of solution similarities between original and revised code guided by CTRL on CodeContests. Left: Distribution of similarity scores for self-critique and our CTRL method. Right: Box plot showing the statistical distribution of similarity scores. Lower scores indicate more substantial revisions.

🔼 The figure illustrates the two-stage training pipeline of the CTRL framework. The first stage involves Supervised Fine-Tuning (SFT), where an initial solution is generated, and its correctness is validated through execution feedback. This feedback is then used to generate critiques that are subsequently utilized for supervised fine-tuning. The second stage is Reinforcement Learning (RL) training, which uses the critic’s feedback to guide the generator in producing improved solutions. This process iteratively refines the solutions using the sandbox environment for validation.
read the caption
Figure 8: Overview of our two-stage training pipeline CTRL.

🔼 Figure 9 illustrates the difference between refinement processes using only discrimination (best-of-n sampling) and those employing both discrimination and critiquing (sequential critique-revision). The left panel shows a best-of-n sampling approach where multiple solutions (y0, y1, y2…yn) are generated independently, and the best solution is selected based on a discrimination function. In contrast, the right panel depicts a sequential critique-revision process. Here, an initial solution (y0) is generated, critiqued, and revised iteratively to produce a sequence of improved solutions (y1, y2…yn) until a satisfactory solution is found. This highlights the iterative nature of using critiques to improve solution quality.
read the caption
Figure 9: Graphical models for refinement processes: (left) only using discrimination (best-of-n𝑛nitalic_n sampling) and (right) using both discrimination and critiquing (sequential critique-revision).

🔼 This figure shows how the accuracy of the majority voting reward calculation improves as the number of votes increases. The x-axis represents the number of votes used in the majority voting process, and the y-axis represents the accuracy of the reward calculation. The graph demonstrates that the accuracy increases significantly as more votes are used. This suggests that the majority voting approach is scalable and robust, meaning it performs reliably and consistently even with large numbers of votes.
read the caption
(a) The effect of the number of votes on the accuracy of majority voting in reward calculation. As the number of votes increases, the accuracy improves significantly, demonstrating the scalability and robustness of the majority voting approach.

More on tables

	Passed	Failed	Macro
Qwen2.5-Coder	88.21	34.16	61.19
CTRL ${}_{\text{SFT}}$	95.54	41.26	68.55
CTRL	93.19	45.02	69.10

🔼 This table presents the performance of the critic model in terms of its ability to discriminate between correct and incorrect code solutions. Specifically, it shows the F1 score (a measure of a test’s accuracy) achieved by the model on the CodeContests dataset. A higher F1 score indicates better discrimination ability.
read the caption
Table 2: Discrimination performance (F1 score, %) on CodeContests.

	CodeContests			LiveCodeBench			MBPP+			Average
	Pass@1	$\Delta_{\uparrow}$	$\Delta_{\downarrow}$	Pass@1	$\Delta_{\uparrow}$	$\Delta_{\downarrow}$	Pass@1	$\Delta_{\uparrow}$	$\Delta_{\downarrow}$	Pass@1
Qwen2.5-Coder as Generator
Zero-shot	7.88	0.00	0.00	30.54	0.00	0.00	77.83	0.00	0.00	38.75
Single-turn Critique-revision
Critique w/ Qwen2.5-Coder	8.36	2.30	1.82	32.14	2.50	0.89	77.83	3.49	3.49	39.45
Critique w/ GPT-4o	10.67	4.85	2.06	32.32	2.32	0.54	77.46	3.81	4.18	40.15
Critique w/ CTRL	11.76	4.73	0.85	33.21	3.39	0.71	78.84	2.43	1.43	41.27
Multi-turn Critique-revision
Critique $\times 5$ w/ Qwen2.5-Coder	9.21	3.76	2.42	29.64	2.14	3.04	76.03	3.81	5.61	38.30
Critique $\times 5$ w/ GPT-4o	12.48	7.03	2.42	32.86	4.82	2.50	74.60	4.34	7.57	39.98
Critique $\times 5$ w/ CTRL	16.24	9.21	0.85	33.39	3.75	0.89	78.68	3.23	2.38	42.77
GPT-4o as Generator
Zero-shot	20.61	0.00	0.00	32.32	0.00	0.00	77.67	0.00	0.00	43.53
Single-turn Critique-revision
Critique w/ Qwen2.5-Coder	20.24	3.52	3.88	35.36	3.93	0.89	76.67	0.85	1.85	44.09
Critique w/ GPT-4o	20.97	2.30	1.94	34.82	2.68	0.18	77.41	1.01	1.27	44.40
Critique w/ CTRL	23.03	4.97	2.55	33.39	2.14	1.07	77.83	0.53	0.37	44.75
Multi-turn Critique-revision
Critique $\times 5$ w/ Qwen2.5-Coder	19.52	5.21	6.30	35.54	5.36	2.14	76.08	1.53	3.12	43.71
Critique $\times 5$ w/ GPT-4o	20.61	3.39	3.39	35.18	3.21	0.36	76.61	2.06	3.12	44.13
Critique $\times 5$ w/ CTRL	25.45	7.88	3.03	34.11	3.21	1.43	77.94	0.79	0.53	45.83

🔼 Table 3 presents a comprehensive comparison of the performance of different code generation models across various benchmarks. The models are evaluated under different configurations, including zero-shot generation and multiple rounds of iterative critique-revision. Critique-revision involves using a critic model to provide feedback to the code generation model, enabling iterative refinement of the generated code. The table shows the success rate (Pass@1) for each model configuration, along with the percentage of initially incorrect solutions that are successfully corrected during critique-revision (Δ↑) and the percentage of initially correct solutions that become incorrect (Δ↓) during the process. The results are averaged over five independent runs to ensure reliability.
read the caption
Table 3: Performance comparison across different generators and benchmarks. We evaluate different configurations, with critique-revision representing an iterative process where a critic model provides feedback to guide solution improvement. Pass@1 shows the success rate, while Δ↑subscriptΔ↑\Delta_{\uparrow}roman_Δ start_POSTSUBSCRIPT ↑ end_POSTSUBSCRIPT and Δ↓subscriptΔ↓\Delta_{\downarrow}roman_Δ start_POSTSUBSCRIPT ↓ end_POSTSUBSCRIPT indicate the percentage of wrong solutions being correctly revised and correct solutions being revised to wrong solutions, respectively. Results are averaged over 5 random seeds.

Generator	Critic			Avg.
Generator	7B	14B	32B	Avg.
7B	-33.33	22.22	-11.11	-7.41
14B	-9.09	-9.09	9.09	-3.03
32B	0.00	30.00	50.00	26.67
Avg.	-14.14	14.38	15.99

🔼 This table presents the relative improvement in pass rate achieved by using a critique-revision approach on CodeContests, compared to a zero-shot approach. It shows the results across various combinations of generator and critic model sizes. Importantly, these results are obtained from inference-only experiments, before any fine-tuning of the models has been performed. This highlights the inherent effectiveness of the critique-revision method even without any training optimization.
read the caption
Table 4: Relative improvement (%) on CodeContests when comparing critique-revision (using critics conditioned on execution feedback) against zero-shot generation, across different generator-critic size combinations. Results are from inference-only experiments before any finetuning.

	Timeout Rate ( $\downarrow$ )	Pass@1 ( $\uparrow$ )
Zero-shot	10.54	30.54
Critique w/ GPT-4o	8.93	32.32
Critique w/ CTRL	16.61	33.21

🔼 Table 5 presents a comparison of the performance of different approaches on the LiveCodeBench benchmark. It shows two key metrics: the percentage of times a solution timed out before completion, and the percentage of times the solution was correct (Pass@1). The table highlights a trade-off between the two approaches shown: the CTRL approach produced more accurate solutions (higher Pass@1), but these solutions were more complex and thus tended to take longer to run, resulting in a higher timeout rate.
read the caption
Table 5: Timeout rate and Pass@1 (%) on LiveCodeBench. While CTRL approach achieves higher pass rates, it tends to generate more comprehensive solutions that take longer to execute.

Methods	Input	Output	Discrimination	Refinement	Critique Supervision
Standard RM (Bradley & Terry, 1952)	$x$ , $y$	$r$	✓	✗	✗
SynRM (Ye et al., 2024)	$x$ , $y$ , $c$	$r$	✓	✗	✓
UltraCM (Cui et al., 2023)	$x$ , $y$	$c$	✗	✓	✓
Shepherd (Wang et al., 2023)	$x$ , $y$	$c$	✗	✓	✓
CriticGPT (McAleese et al., 2024)	$x$ , $y$	$c$	✗	✓	✓
CLoud (Ankner et al., 2024)	$x$ , $y$	$c$ , $r$	✓	✗	✓
Critic-RM (Yu et al., 2024)	$x$ , $y$	$c$ , $r$	✓	✗	✗
CTRL (Ours)	$x$ , $y$	$c$	✓	✓	✗

🔼 This table compares different approaches to providing feedback for improving large language model outputs. It contrasts reward models, which provide only a scalar reward, with generative reward models that also output critiques. It further distinguishes these from critic models that focus solely on critique generation, highlighting the differences in their feedback mechanisms and training methodologies. The table shows the input and output of each method, indicating whether it performs discrimination (ranking solutions) and refinement (guiding improvements) tasks, as well as whether it utilizes critique supervision during training.
read the caption
Table 6: Comparison of reward models, generative reward models, and critic models.

Execution Result	Hint
Success (100%)	The draft solution is correct. A concise and positive feedback is recommended.
Failure (0%)	The draft solution is entirely wrong. A concise feedback requesting a fresh restart is recommended.
Partial Success	Input: {input} Expected Output: {expected_output} Actual Output: {actual_output}
Runtime Error	The code block: “‘python {code_block} ”’ raised {error}.

🔼 This table details how execution outcomes from a code sandbox are translated into textual hints used to guide the generation of critiques. It shows the mapping between three possible execution results (success, failure, partial success) and the corresponding hint templates provided to the LLM to assist in generating a critique.
read the caption
Table 7: Mapping between execution results and hint templates used for critique synthesis.

Parameter	Value
Learning Rate	2 $\times$ 10^-5
Learning Rate Schedule	Cosine
Training Batch Size	256
Maximum Token Length	2,048
Training Epochs	1
Mixed Precision Format	bfloat16

🔼 Table 8 presents the hyperparameters used during the supervised fine-tuning (SFT) stage of the CTRL framework. These hyperparameters control various aspects of the training process, including the learning rate, batch size, optimizer, and others. They are crucial for guiding the critic model’s learning to effectively generate helpful and accurate critiques of code generation.
read the caption
Table 8: SFT Hyperparameters.

Parameter	Value
Training Batch Size	1,024
Mini-Batch Size	256
Group Size	8
Learning Rate	1 $\times$ 10^-5
KL Coefficient	0.001
Maximum Prompt Length	1,536
Maximum Response Length	768
Temperature	1.0
Training Epochs	2

🔼 Table 9 presents the hyperparameters used during the reinforcement learning (RL) phase of the CTRL training process. It details the settings for various parameters impacting the RL training, such as the learning rate, batch size, and the maximum length of tokens used in the process.
read the caption
Table 9: RL Hyperparameters.

Problem & Solution

Critique

⬇ You had n positive integers a_1, a_2, ..., a_n arranged in a circle. For each pair of neighboring numbers (a_1 and a_2, a_2 and a_3, ..., a_{n - 1} and a_n, and a_n and a_1), you wrote down: are the numbers in the pair equal or not. Unfortunately, you’ve lost a piece of paper with the array a. Moreover, you are afraid that even information about equality of neighboring elements may be inconsistent. So, you are wondering: is there any array a which is consistent with information you have about equality or non-equality of corresponding pairs?

⬇

def can_form_array(s):

n = len(s)

# We will try to assign values to the array a

# Start with assigning 1 to the first element

a = [1] * n

# Try to assign values based on the given conditions

for i in range(n):

if s[i] == ’E’:

a[(i + 1) %

else:

a[(i + 1) %

# Check if the last and first elements are consistent with s[n-1]

if s[-1] == ’E’ and a[0] != a[-1]:

return "NO"

if s[-1] == ’N’ and a[0] == a[-1]:

return "NO"

return "YES"

def main():

import sys

input = sys.stdin.read().splitlines()

t = int(input[0])

results = []

for i in range(1, t + 1):

s = input[i]

results.append(can_form_array(s))

for result in results:

print(result)

if __name__ == "__main__":

main()

⬇ Analysis: The provided solution attempts to construct an array based on the sequence of ’E’ and ’N’ but does not correctly handle the circular nature of the array and the constraints imposed by these characters. Specifically, the approach does not ensure consistency across the entire circular arrangement, particularly at the boundary where the last element connects back to the first. The code assigns values to the array elements based on whether the current character is ’E’ or ’N’, but it does not account for potential conflicts that arise when the array wraps around. This means that the final check between the first and last elements might fail due to inconsistencies introduced earlier in the array construction process. Improvement suggestions: 1. Consider using a more systematic approach to handle the circular nature of the array. One possible method is to use a graph traversal algorithm, treating each position in the array as a node and each ’E’ or ’N’ as an edge with a label indicating equality or inequality. 2. Use a union-find data structure to manage equivalence classes of indices that must hold the same value due to ’E’ connections. 3. Iterate through the string and apply the rules: if ’E’, ensure the indices are in the same set; if ’N’, ensure they are in different sets. 4. After processing the string, verify that no conflicts exist in the union-find structure, particularly focusing on the circular connection between the first and last elements. 5. If no conflicts are found, it is possible to construct an array that satisfies the conditions; otherwise, it is not. Overall judgment: Incorrect

🔼 This table presents a sample problem from the CodeContests dataset, along with the solution generated by the Qwen2.5-Coder model and the critique provided by the CTRL critic. It showcases an example of how the CTRL framework identifies flaws in a generated code solution and offers actionable suggestions for improvement. The problem statement, the code generated by Qwen2.5-Coder, and the critique from CTRL are all displayed for analysis.
read the caption
Table 10: A sample problem from CodeContests (Li et al., 2022), with by the solution generated by Qwen2.5-Coder and the critique provided by the CTRL critic.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

LLM Self-Critique#

CTRL Framework#

Iterative Refinement#

GRPO Optimization#

Future Directions#

More visual insights#

Full paper#