TL;DR#
Current methods in Reinforcement Learning from Human Feedback (RLHF) for aligning Large Language Models (LLMs) with human values often rely on approximate reward models and inefficient data sampling. This leads to inconsistencies in guiding policy toward maximizing human values, and preference labeling is expensive. The paper focuses on solving the challenge of effective data collection and use for human labeling in RLHF.
To address these issues, the paper proposes PILAF (Policy-Interpolated Learning for Aligned Feedback), a novel response sampling strategy. PILAF generates responses by interpolating between the current policy and a reference policy for balanced exploration and exploitation. Theoretically, PILAF aligns reward model optimization with value optimization, offering optimal performance from an optimization and statistical perspective. Empirically, PILAF demonstrates strong performance in iterative and online RLHF settings, surpassing existing methods in terms of reward and efficiency, and reducing annotation and computation costs.
Key Takeaways#
Why does it matter?#
This paper is crucial for RLHF researchers as it introduces PILAF, a novel sampling method that significantly improves the efficiency and effectiveness of reward model training. This addresses a critical challenge in RLHF, where high-quality preference data is expensive and hard to obtain, impacting the overall performance of LLMs. PILAF’s theoretical grounding and strong empirical results provide a valuable contribution to the field, opening new avenues for research in sample-efficient reinforcement learning and model alignment. It’s particularly relevant given the growing interest in aligning LLMs with human values.
Visual Insights#

🔼 This figure provides a high-level overview of the PILAF approach. Panel (a) illustrates a standard RLHF training loop, where the language model’s policy is iteratively improved by collecting human preference data via pairwise comparisons. The goal of the paper is to improve the sampling method used to obtain these preference comparisons. Panel (b) introduces the PILAF method, showing how it generates response pairs for comparison by interpolating between a reference policy (a pre-trained or well-understood model) and the current policy. This interpolation balances exploration (trying diverse responses) and exploitation (focusing on responses likely to be highly preferred). Panel (c) summarizes the theoretical analysis showing that PILAF’s sampling strategy makes the collected data more informative and leads to faster convergence towards aligning the language model with human preferences.
read the caption
Figure 1: Overview of our approach. (a) We consider a full RLHF training setup, where a language model (LM) policy is iteratively refined through active data collection. Our goal is to develop an optimal response sampling method for preference labeling. (b) We introduce PILAF, which generates responses by interpolating between the current policy and a reference policy, balancing exploration and exploitation. (c) Our theoretical analysis shows that T-PILAF aligns the parameter gradient with the steepest direction for maximizing human values and achieves more favorable convergence in regions of high sensitivity.
| Yunzhen Feng† | Ariel Kwiatkowski∗ | Kunhao Zheng∗ | Julia Kempe⋄ | Yaqi Duan⋄ |
|---|---|---|---|---|
| NYU | Meta FAIR | Meta FAIR | Meta FAIR & NYU | NYU |
🔼 This table compares the computational cost and annotation effort required for generating a single preference pair using different sampling methods. It contrasts the standard vanilla approach, which samples two responses and requires two annotations, with methods such as best-of-N, which sample multiple responses but ultimately only uses two for labeling. The table highlights that PILAF, while having slightly higher sampling costs (3 forward passes compared to Vanilla’s 2), requires fewer annotations (2, same as vanilla) and is therefore more efficient than other methods such as Best-of-N which can significantly increase the annotation cost.
read the caption
Table 1: A cost summary of PILAF and sampling methods from related works. Best-of-N method in Xiong et al. (2024) uses the oracle reward to score all candidate responses, then selects the highest- and lowest-scoring ones—instead of providing a preference label for only two responses. We restrict the oracle to providing only preference labels. Thus, we create a Best-of-N variant that uses the DPO internal reward for selection and then applies preference labeling, with an annotation cost of 2. We compare with this variant in the experiment.
In-depth insights#
Optimal Sampling#
Optimal sampling strategies in reinforcement learning from human feedback (RLHF) are crucial for efficient and effective model alignment. The core challenge lies in balancing exploration and exploitation when querying human labelers for preferences. Uniform sampling, while simple, often leads to inefficient data collection, failing to prioritize informative comparisons. Optimal sampling methods aim to address this by strategically selecting pairs of model outputs to compare, focusing on areas where human preferences are most uncertain or where the model’s performance is most sensitive. This targeted approach reduces the number of human evaluations needed, while simultaneously improving the quality of the resulting reward model. Theoretical analysis often underpins these methods, demonstrating optimality through optimization or statistical perspectives. Such analyses ensure that the sampling strategy effectively guides the model toward aligning with human values, reducing variance and increasing stability in the learning process. Key considerations include the computational cost of sampling and the trade-off between exploration and exploitation. Effective optimal sampling leads to significant improvements in sample efficiency and reduced annotation costs in RLHF.
RLHF Alignment#
Reinforcement Learning from Human Feedback (RLHF) aims to align large language models (LLMs) with human values. A core challenge is the inherent inaccessibility of true human preferences, necessitating approximation through reward models learned from preference data. RLHF alignment, therefore, focuses on effectively translating human feedback into a reward signal that guides the LLM toward desirable behavior. This involves careful consideration of data collection strategies (sampling methods), which directly impact the quality and informativeness of the learned reward model. Suboptimal sampling can lead to misaligned gradients, hindering the LLM’s progress toward true human alignment. Effective RLHF alignment requires not only sophisticated reward modeling techniques but also a principled approach to preference data generation that balances exploration and exploitation while maximizing the utility of limited human annotation. This highlights the interplay between theoretical analysis and practical implementation, demanding both strong theoretical grounding and efficient algorithms for response sampling.
Theoretical Analysis#
A theoretical analysis section in a research paper would rigorously justify the proposed method’s efficacy. It would likely involve mathematical proofs demonstrating optimality or convergence properties. For example, it might show that the method’s parameter updates converge to the optimal solution under specific conditions, or that it minimizes a well-defined loss function. The analysis should address both optimization and statistical aspects: how efficiently the method approaches the optimum (optimization) and how reliable and precise its estimates are despite noise and limited data (statistical). This section would ideally highlight the theoretical guarantees offered by the proposed method, emphasizing its advantages over existing approaches. Finally, the theoretical analysis will clarify the key assumptions made and their impact on the results, offering a deeper understanding of the method’s strengths and limitations.
DPO Experiments#
In a hypothetical research paper section titled ‘DPO Experiments’, one would expect a thorough evaluation of Direct Preference Optimization (DPO) methods. The experiments should involve a range of tasks and datasets to assess the performance of DPO against established RLHF techniques. Key aspects would include comparing reward model accuracy, policy performance, and sample efficiency. The experiments should meticulously control for variables such as dataset size, reward model complexity, and choice of optimization algorithm, to ensure robust and meaningful conclusions. A detailed analysis of results should include statistical significance testing and error bars to validate findings. Furthermore, ablation studies would be important for isolating the impact of different aspects of DPO on performance. The discussion section would critically examine the results, highlighting limitations and providing insights into scenarios where DPO excels or falls short. Overall, a well-structured ‘DPO Experiments’ section would establish a comprehensive understanding of DPO’s strengths and weaknesses and guide future research directions.
Future of PILAF#
The future of PILAF hinges on several key areas. Extending PILAF’s applicability to other RLHF paradigms beyond DPO, such as PPO and KTO, is crucial. This would broaden its impact and demonstrate its generalizability as a superior sampling method. Addressing the computational cost of PILAF, particularly for larger language models, is vital. While PILAF demonstrates significant gains in efficiency, further optimizations are needed to make it truly scalable for industrial applications. Investigating PILAF’s performance with real human feedback, instead of relying on proxy models, would validate its effectiveness in real-world scenarios and strengthen its practical implications. Finally, exploring theoretical extensions of PILAF to provide even stronger theoretical guarantees and address potential limitations, such as sensitivity to the choice of reference policy, would further enhance its robustness and reliability.
More visual insights#
More on figures

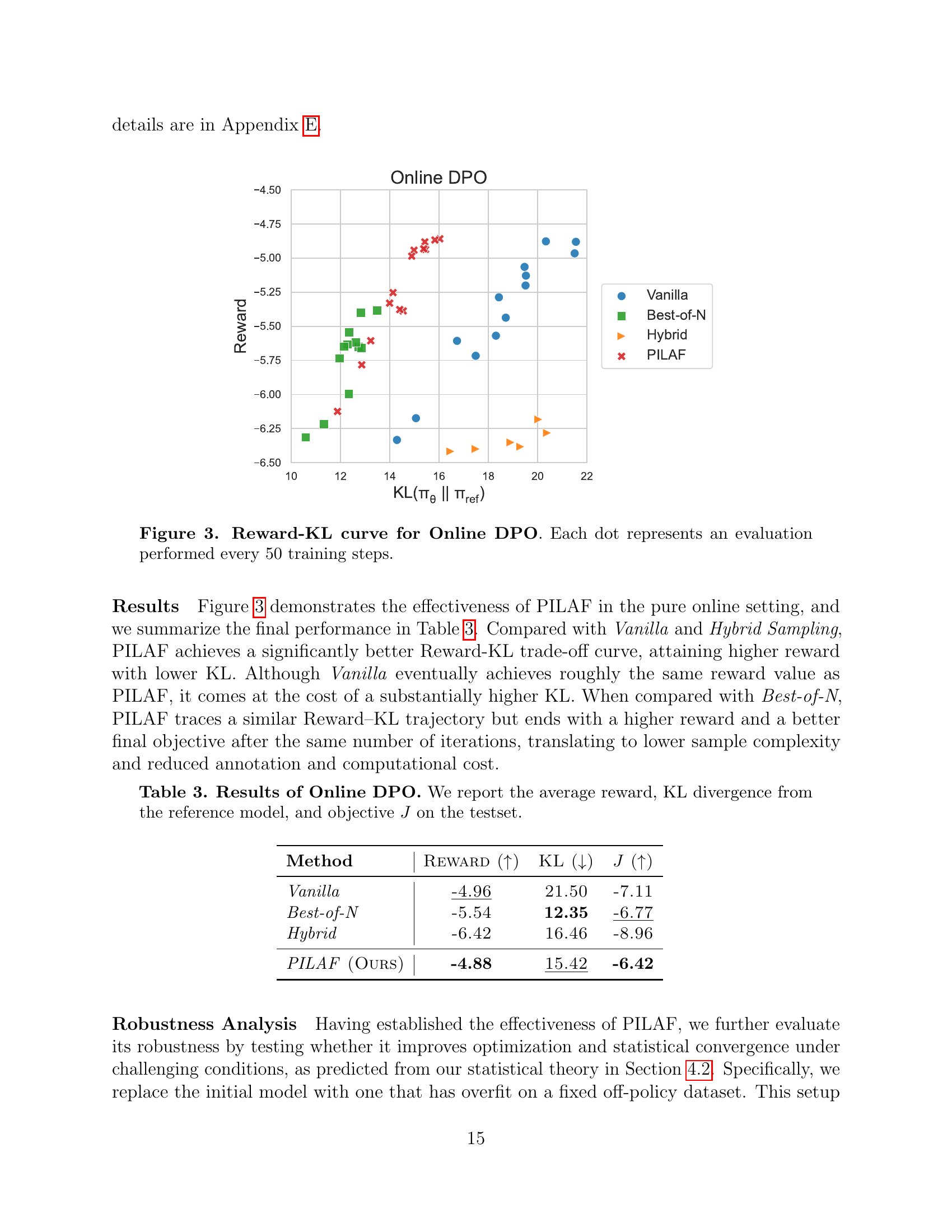
🔼 This figure shows the reward and KL divergence during iterative Direct Preference Optimization (DPO). All training runs begin from the same initial model, trained using vanilla sampling in the first iteration. Each point on the graph represents a model’s performance after 50 training steps. The x-axis represents the KL divergence from a reference model, which measures how different the current policy is from a baseline. The y-axis represents the reward achieved by the model on a test set. The plot illustrates the learning trajectories of different sampling methods, including PILAF and various baseline methods, showcasing PILAF’s superior performance in reaching higher reward values while maintaining a relatively low KL divergence.
read the caption
Figure 2: Reward-KL curve for Iterative DPO. All training runs start from the same model obtained at the end of the first iteration via Vanilla Sampling. Each dot represents an evaluation performed every 50 training steps.

🔼 This figure shows the reward and KL divergence (relative to the reference model) during online DPO training. Each point represents the model’s performance after 50 gradient steps. The plot illustrates how the reward and KL change as the policy is optimized, showcasing the learning progress and the model’s closeness to the reference model. Different sampling methods can lead to different reward-KL tradeoffs.
read the caption
Figure 3: Reward-KL curve for Online DPO. Each dot represents an evaluation performed every 50 training steps.

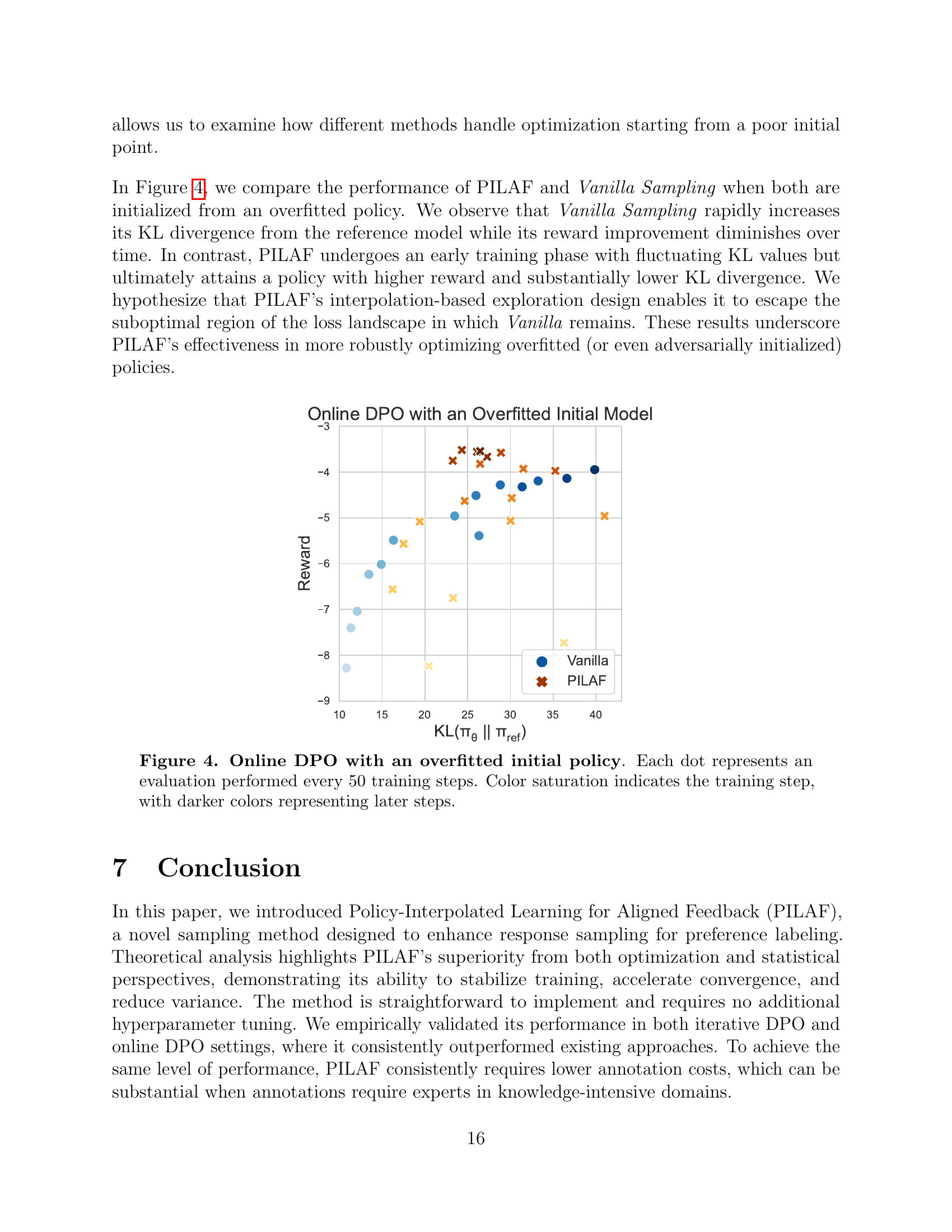
🔼 This figure displays the results of an online direct preference optimization (DPO) experiment where the initial policy model is overfitted. The x-axis shows the KL divergence between the current policy and a reference policy, illustrating the difference between the two policies. The y-axis represents the average reward obtained by the policy. Each point on the graph corresponds to an evaluation of the policy after 50 gradient steps of training. The color intensity of the points gradually darkens to visualize the training progression, with darker shades representing later steps in the training process. This experiment aims to show the robustness of the PILAF method against an initially overfitted model, comparing its performance to standard Vanilla sampling.
read the caption
Figure 4: Online DPO with an overfitted initial policy. Each dot represents an evaluation performed every 50 training steps. Color saturation indicates the training step, with darker colors representing later steps.
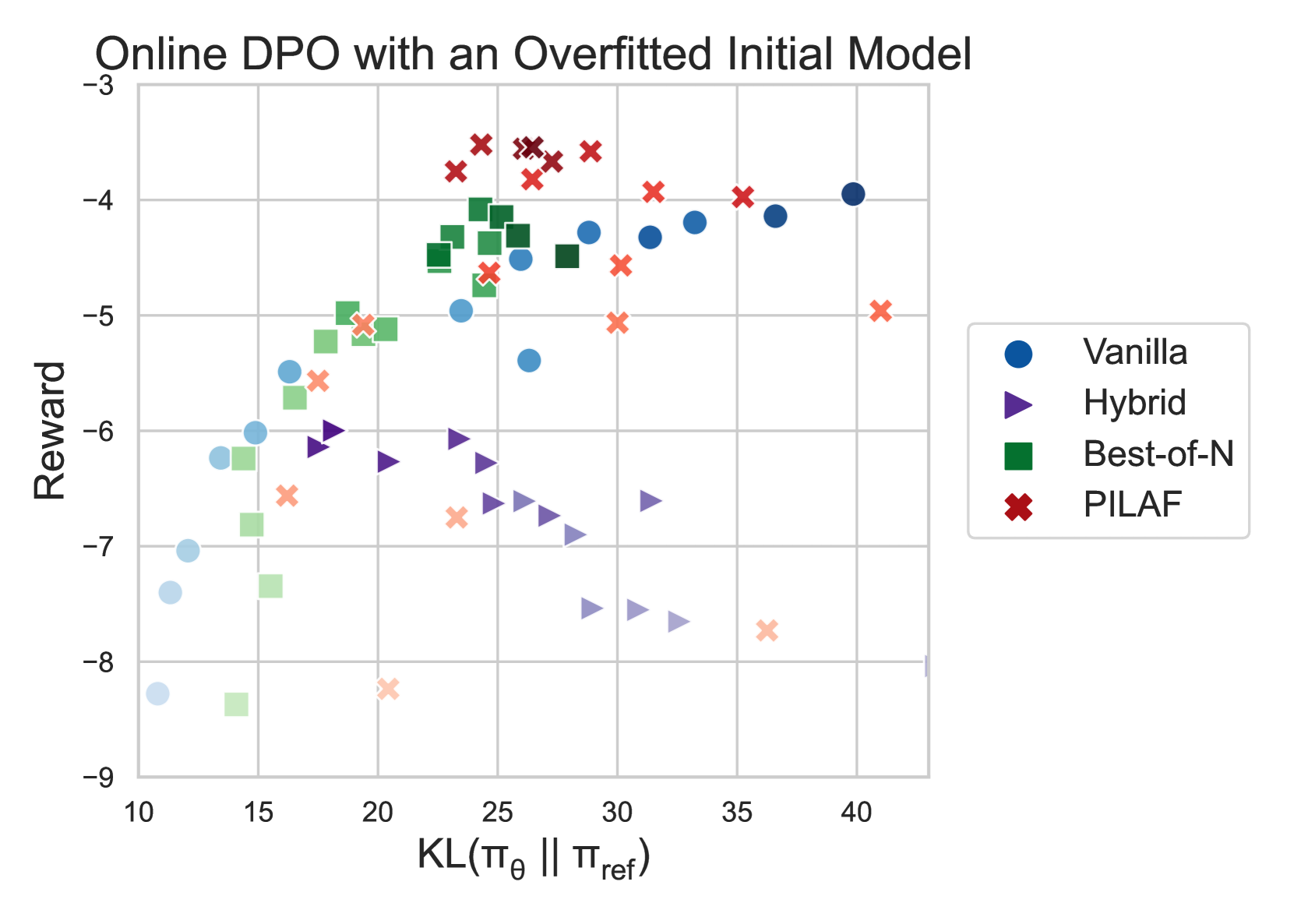
🔼 This figure displays the results of an online direct preference optimization (DPO) experiment where the initial policy model is overfitted. The x-axis represents the KL divergence between the learned policy and a reference policy, while the y-axis shows the reward achieved by the learned policy. Each point in the plot corresponds to an evaluation performed after every 50 training steps. The color intensity of the points increases with the training step, providing a visual representation of the model’s learning progression over time. This visualization allows comparison of the performance of different sampling methods when starting from a suboptimal initial policy.
read the caption
Figure 5: Online DPO with an overfitted initial policy. Full results of the Figure 4. Each dot represents an evaluation performed every 50 training steps. Color saturation indicates the training step, with darker colors representing later steps.
More on tables
| Method | Sampling Cost | Annotation Cost | ||
|---|---|---|---|---|
| Vanilla (Rafailov et al., 2023) | 2 | 2 | ||
| Best-of-N (Xiong et al., 2024), N=8 | best of | worst of | 8 | 8* |
| Best-of-N (with DPO reward), N=8 | best of | worst of | 8 | 2 |
| Hybrid (Xie et al., 2024) | 2 | 2 | ||
| PILAF (OURS) | 3 | 2 |
🔼 This table presents the quantitative results of the iterative Direct Preference Optimization (DPO) experiments. Three key metrics are reported for each of four different sampling methods: Vanilla, Best-of-N, Hybrid, and PILAF. The average reward achieved by the language model on a held-out test set is shown. Lower KL divergence indicates better alignment of the learned policy with the reference policy. Finally, the objective function J (combining reward and KL divergence) reflects the overall performance. Higher values for reward and J indicate better performance, whereas lower KL divergence indicates better alignment.
read the caption
Table 2: Results of Iterative DPO. We report the average reward, KL divergence from the reference model, and objective J𝐽Jitalic_J on the testset. Higher reward and J𝐽Jitalic_J are better, while lower KL divergence is better. We use boldface to indicate the best result and underline to denote the second-best result.
| Method | Reward () | KL () | () |
|---|---|---|---|
| Vanilla | -10.16 | 35.20 | -13.68 |
| Best-of-N | -10.13 | 32.38 | -13.37 |
| Hybrid | -10.51 | 22.86 | -12.80 |
| PILAF (Ours) | -9.80 | 25.01 | -12.30 |
🔼 This table presents the results of the Online Direct Preference Optimization (DPO) experiments. It shows a comparison of different sampling methods (Vanilla, Best-of-N, Hybrid, and PILAF) across three key metrics: the average reward achieved by the trained language model (higher is better), the KL divergence from the reference model (lower is better, indicating closer alignment), and the overall objective function J (higher is better, combining reward and regularization). The results are calculated on a held-out test set.
read the caption
Table 3: Results of Online DPO. We report the average reward, KL divergence from the reference model, and objective J𝐽Jitalic_J on the testset.
Full paper#