TL;DR#
Large Language Models (LLMs) are powerful but computationally expensive. Mixture-of-Experts (MoE) models offer a solution by activating only a subset of parameters during inference, thus reducing computational costs. However, creating effective MoE models often requires extensive training data and resources. This limits their practical use.
The paper introduces CMOE, a novel framework that tackles these issues. CMOE efficiently creates MoE models from pre-trained dense models without the need for extensive retraining. It achieves this through efficient expert grouping based on neuron activation patterns and a training-free routing mechanism derived from activation statistics. CMOE’s lightweight adaptation allows it to quickly recover performance with minimal fine-tuning, making it a practical and efficient approach for deploying LLMs.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel and efficient method for creating Mixture-of-Experts (MoE) models from existing large language models (LLMs). This is significant because MoE models offer improved efficiency for LLM inference, a critical concern in the field. The method is also training-free and resource-light, making it practical for widespread adoption. The research opens new avenues for efficient LLM deployment and optimization, particularly important given the ever-increasing size of LLMs.
Visual Insights#

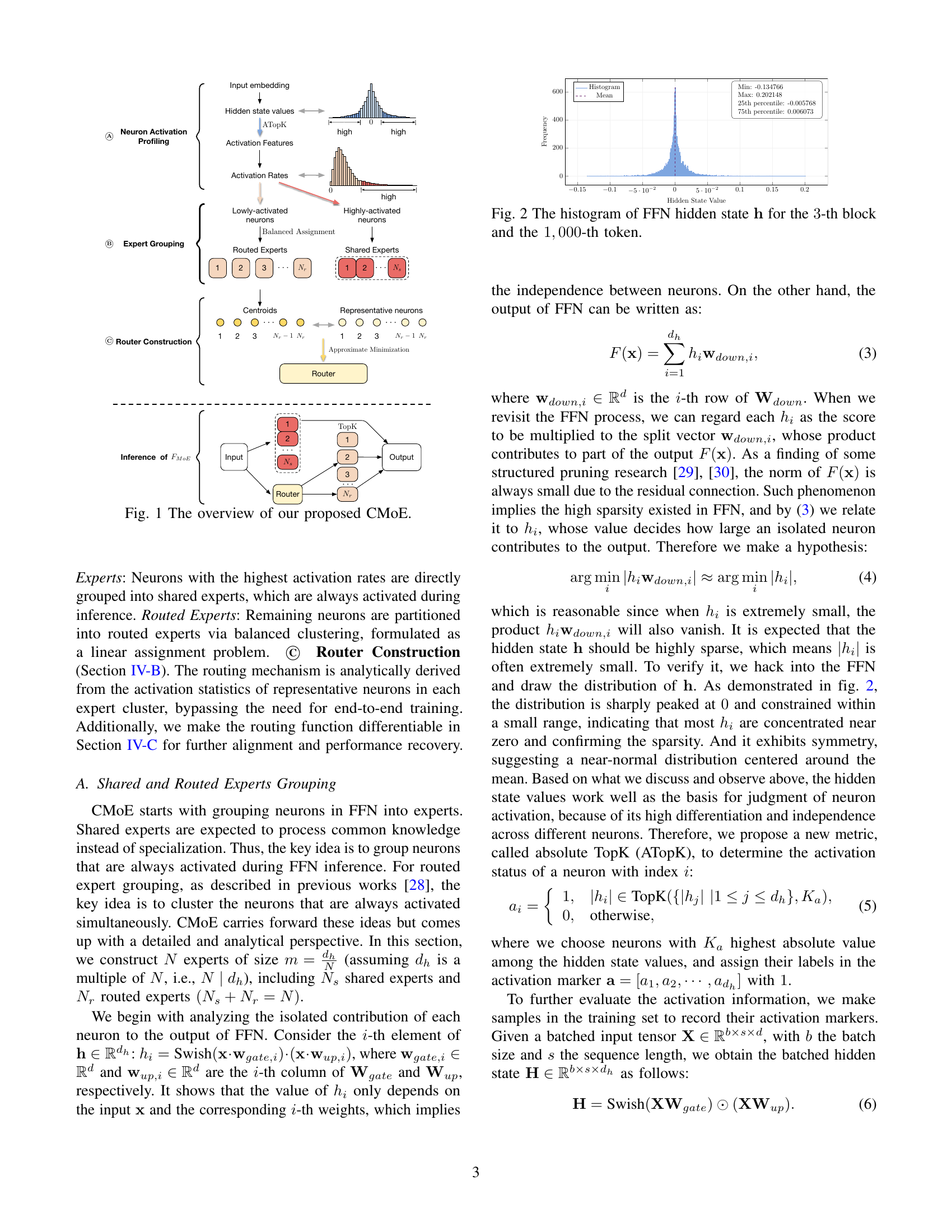
🔼 This figure provides a high-level overview of the proposed Carved Mixture-of-Experts (CMoE) model. It illustrates the key steps involved in transforming a dense feed-forward network (FFN) into a sparse MoE architecture. The process begins with neuron activation profiling to identify neurons with high and low activation rates. These neurons are then grouped into shared and routed experts, respectively. A training-free routing mechanism is constructed using activation statistics from representative neurons in each expert cluster. Finally, the CMoE model performs inference by activating only a subset of experts per token, achieving efficient and sparse computation.
read the caption
Figure 1: The overview of our proposed CMoE.
In-depth insights#
MoE Carving#
MoE carving, as a novel approach, offers a compelling alternative to traditional MoE model training. Instead of training a MoE model from scratch, a significant computational undertaking, it leverages existing dense models. This reduces training time and resource requirements dramatically. The method involves a strategic reorganization of neurons within the dense model’s FFN layers to form shared and routed experts, a process informed by neuron activation patterns. The training-free routing mechanism, constructed using activation statistics, further enhances efficiency, circumventing the need for extensive router training. Although initial results may not perfectly match the dense model’s performance, lightweight fine-tuning rapidly bridges this gap, achieving high accuracy with modest computational needs. This approach presents a promising path to realizing the benefits of MoE architectures in resource-constrained environments, making large language models more accessible and practical.
Router Design#
Effective router design is crucial for Mixture-of-Experts (MoE) models to achieve efficiency and performance. A poorly designed router can lead to uneven load balancing across experts, resulting in wasted computation and suboptimal accuracy. The paper emphasizes a training-free approach, leveraging the activation statistics of the dense model to derive the router’s initial parameters, significantly reducing the training time and resource needs. This contrasts sharply with methods requiring extensive pre-training. The strategy of using representative neurons for router initialization is key, as it effectively captures essential features without requiring extensive computations. Furthermore, the adoption of a differentiable routing function ensures compatibility with backpropagation, enabling straightforward fine-tuning to further enhance the model’s performance. The use of load-balancing techniques is also highlighted as essential for ensuring computational efficiency and preventing bottlenecks within the MoE architecture. The balanced linear assignment problem approach employed demonstrates a thoughtful optimization strategy for allocating neurons to experts to achieve efficiency and performance.
Data Efficiency#
The research emphasizes data efficiency as a crucial aspect of making Mixture-of-Experts (MoE) models practical. Traditional MoE training demands massive datasets, hindering widespread adoption. This work’s innovation lies in its ability to carve MoE models from pre-trained dense models using a minimal amount of additional data, significantly reducing the data requirements. The effectiveness is demonstrated by achieving high performance with only 2048 samples for fine-tuning, highlighting the substantial reduction in data needs compared to training MoE models from scratch. Lightweight fine-tuning further enhances performance, showcasing that even modest amounts of data can lead to impressive results. The training-free router construction also contributes to data efficiency by eliminating the need for extensive router training data, making the method readily applicable in resource-constrained environments. Ultimately, the focus on data efficiency positions the proposed approach as a more accessible and practical alternative to traditional MoE methods.
Ablation Studies#
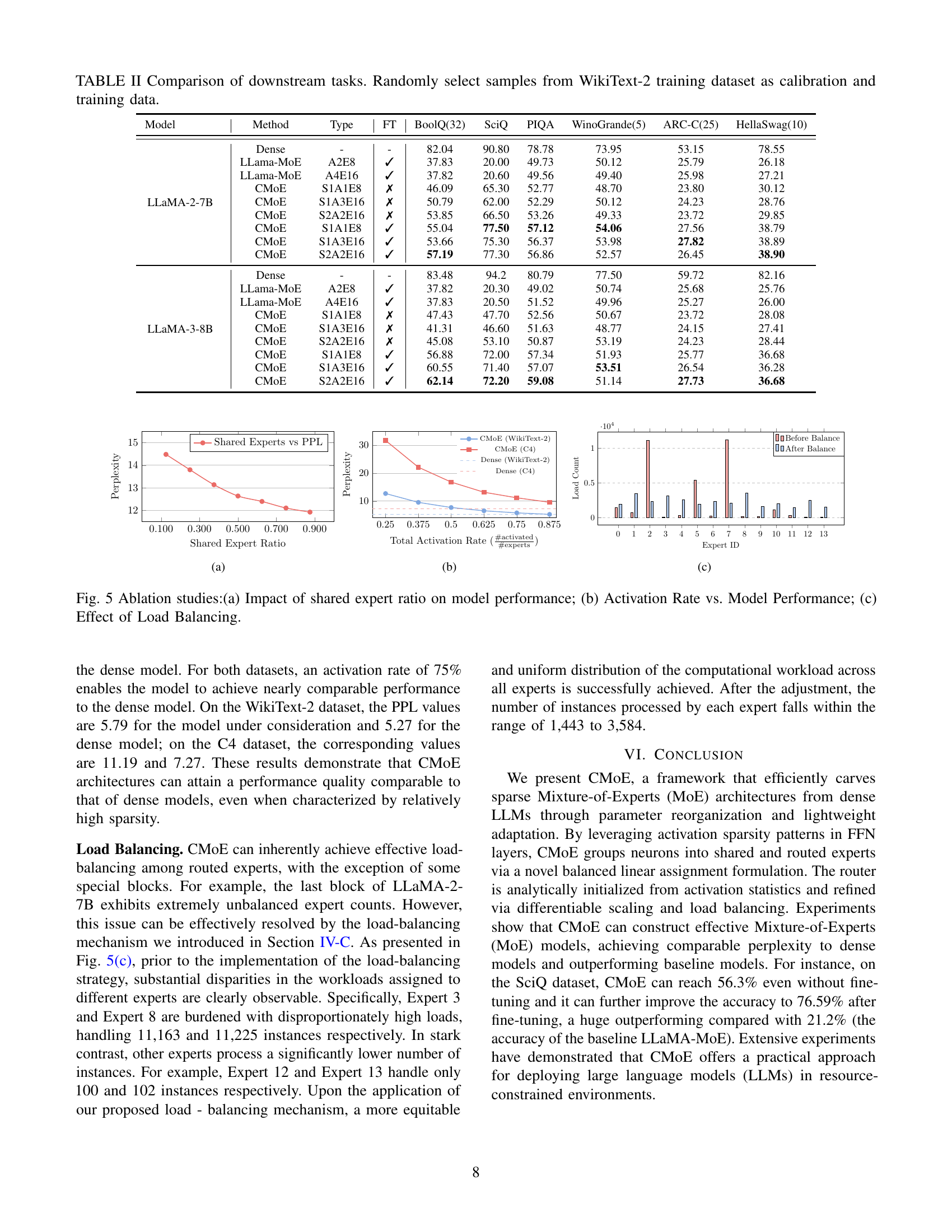
The ablation study section of the research paper is crucial for understanding the contribution of individual components to the overall model performance. It systematically removes or alters specific parts of the model (e.g., different expert ratios, activation rates, training data sizes) to observe their impact on key metrics such as perplexity and downstream task accuracy. This helps to isolate the effects of each component and assess their relative importance. The results from these experiments not only validate design choices but also reveal potential areas for improvement or further research. For instance, the study of various expert ratios can show optimal balance between shared and routed experts, and analysis of activation rates can determine the trade-off between model sparsity and performance. The impact of training data size highlights the computational cost versus performance gain, indicating whether more data yields diminishing returns or justifies further computational investment. A well-designed ablation study is critical for establishing the model’s robustness and justifying its design decisions. By meticulously varying parameters and analyzing results, the researchers provide compelling evidence supporting their claims and contribute valuable insights into the dynamics of the model architecture.
Future Work#
Future research could explore more sophisticated expert grouping strategies beyond activation rate, perhaps incorporating semantic analysis or task-specific activation patterns to improve expert specialization. Investigating alternative routing mechanisms that are more efficient and robust than simple TopK selection is crucial, potentially exploring differentiable routing functions with better load balancing properties. Extensive experimentation across a broader range of LLMs and downstream tasks is needed to validate the generalizability of CMoE. Further work could focus on optimizing the trade-off between model sparsity and performance, investigating different levels of sparsity and the impact on various applications. Finally, exploring CMoE’s integration with other model compression techniques like quantization and pruning is a promising avenue for even greater efficiency gains. Addressing potential challenges in deploying CMoE in real-world systems with limited resources and stringent latency constraints should be a priority.
More visual insights#
More on figures

🔼 This histogram visualizes the distribution of hidden state values (h) for a specific neuron within the 3rd feed-forward network (FFN) block of a large language model (LLM), at the 1000th token during processing. The x-axis represents the hidden state values (h), and the y-axis represents their frequency. The histogram illustrates the high sparsity of activation in FFN layers, with the majority of values concentrated near zero. This observation supports the core hypothesis of the paper, which is that dense LLMs have significant activation sparsity that can be leveraged for efficient model compression through mixture-of-experts (MoE) techniques. The figure’s details demonstrate the prevalence of near-zero activation values, confirming the existence of significant sparsity in the network’s hidden layers, and hence the potential for using MoE methods.
read the caption
Figure 2: The histogram of FFN hidden state 𝐡𝐡\mathbf{h}bold_h for the 3333-th block and the 1,00010001,0001 , 000-th token.

🔼 Figure 3 shows the distribution of activation rates for neurons within the third feed-forward network (FFN) block of a large language model (LLM). Each neuron’s activation rate (μ) represents the frequency with which it is activated across a subset of input tokens. The histogram visualizes this distribution, revealing a highly skewed distribution with most neurons exhibiting low activation rates and a long tail indicating a few highly active neurons (those that are activated often). The parameter Ka = 1000 controls the number of top neurons considered when calculating activation rates. This figure supports the paper’s claim of significant activation sparsity in LLMs, motivating the development of mixture-of-experts (MoE) models.
read the caption
Figure 3: The histogram of activation rates 𝝁𝝁\bm{\mu}bold_italic_μ for the 3333-th block with Ka=1,000subscript𝐾𝑎1000K_{a}=1,000italic_K start_POSTSUBSCRIPT italic_a end_POSTSUBSCRIPT = 1 , 000.

🔼 This figure illustrates the relationship between the amount of training data used and both the model’s performance (measured by perplexity) and the time it takes to construct the model. It shows that while increasing the training data significantly improves the model’s performance initially, the gains diminish as the amount of data increases. Moreover, the construction time increases non-linearly with the amount of training data. This demonstrates a trade-off: substantial performance improvements can be achieved with a relatively small amount of data, but further improvements require disproportionately more time and resources.
read the caption
Figure 4: Trade-off between Model Performance and Construction Time with Increasing Training Data.

🔼 This figure presents ablation study results to analyze the impact of different factors on the performance of the proposed CMoE model. Specifically, it shows three subfigures: (a) Impact of shared expert ratio: This plot illustrates how varying the proportion of shared experts within the activated experts affects model performance (perplexity). It demonstrates the relationship between the ratio of shared experts and the model’s performance. (b) Activation rate vs. model performance: This plot investigates the relationship between the total activation rate (the combined proportion of shared and activated routed experts) and the model’s performance (perplexity) on two different datasets (WikiText-2 and C4). It assesses the effect of different activation rates on model perplexity, showing how sparsity impacts performance. (c) Effect of load balancing: This visualization compares the distribution of computational workload across experts before and after implementing the proposed load-balancing mechanism. It highlights how the load-balancing strategy improves the even distribution of tasks among the experts, increasing efficiency and potentially parallelization.
read the caption
Figure 5: Ablation studies:(a) Impact of shared expert ratio on model performance; (b) Activation Rate vs. Model Performance; (c) Effect of Load Balancing.
Full paper#