QuEST: Stable Training of LLMs with 1-Bit Weights and Activations

2502.05003

Andrei Panferov et el.

🤗 2025-02-10

TL;DR
#

Large language models (LLMs) are computationally expensive. One approach to reduce costs is using quantized representations, but existing Quantization-Aware Training (QAT) methods struggle to achieve high accuracy at low bit-widths, often plateauing around 8-bits. The open problem is achieving accuracy comparable to higher-precision models while significantly reducing computational resources.

The paper introduces QuEST, a novel QAT method that solves this problem. QuEST uses Hadamard normalization and a new trust gradient estimator for accurate and fast quantization. It demonstrates that LLMs can be trained successfully with only 1-bit weights and activations, surpassing existing accuracy at much lower model sizes and significantly reducing inference cost. Experiments show QuEST induces stable scaling laws, making it highly efficient across different hardware precisions.

Key Takeaways
#

Why does it matter?
#

This paper is important because it presents QuEST, a novel method for training large language models (LLMs) with significantly reduced computational costs. QuEST achieves this by employing 1-bit weights and activations during training, a significant advancement over existing methods that often plateau at 8-bits. The research opens new avenues for efficient LLM training and deployment, addressing a critical challenge in the field and influencing future research directions.

Visual Insights
#

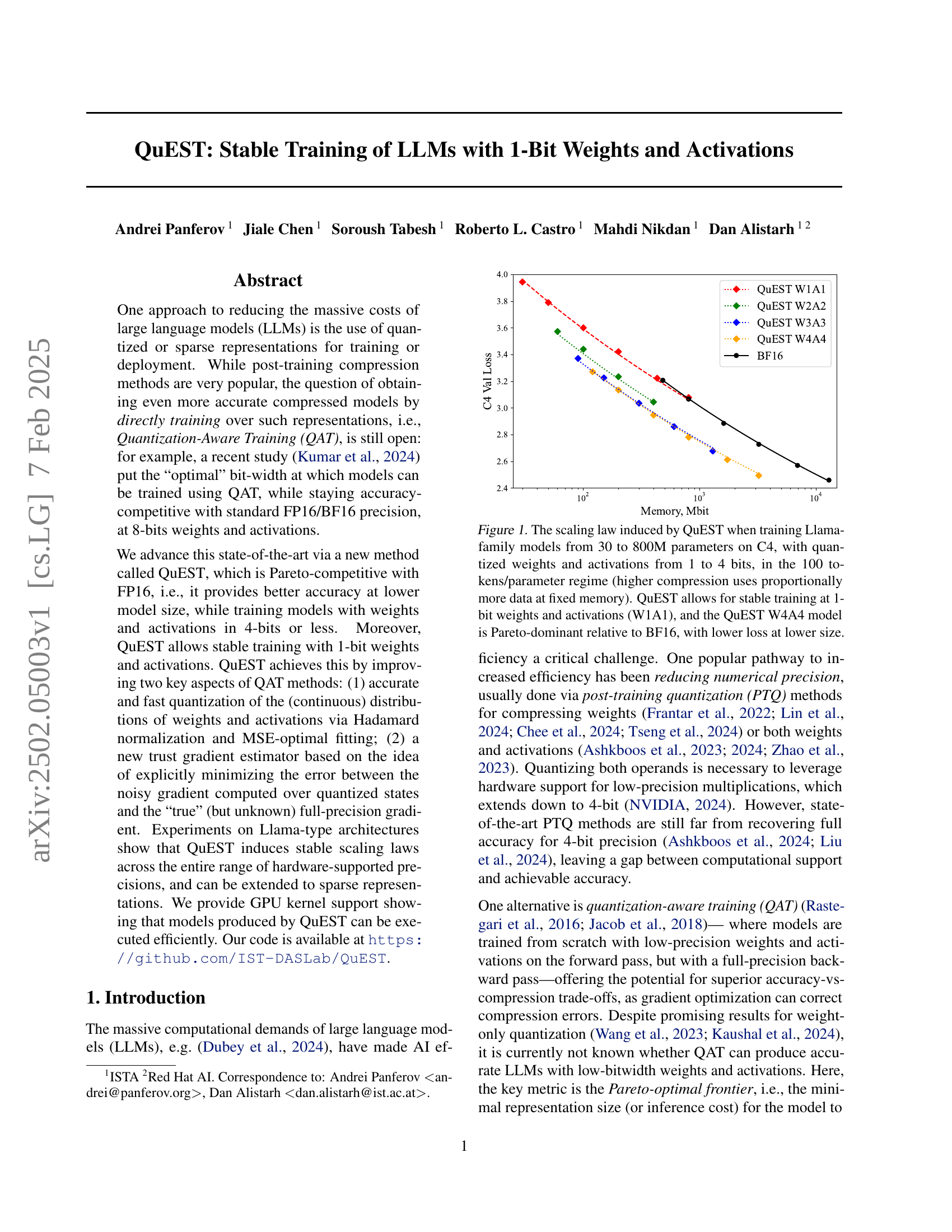
🔼 This figure illustrates the scaling laws observed when training Llama-family language models using QuEST, a novel quantization-aware training method. Models ranging in size from 30 million to 800 million parameters were trained on the C4 dataset. QuEST allows for the use of quantized weights and activations, with bit depths from 1 to 4 bits. The experiment was conducted in a regime where the number of training tokens was 100 times the number of model parameters. Importantly, the graph shows that higher compression ratios (fewer bits) require proportionally more training data to achieve comparable performance. The results demonstrate that QuEST achieves stable training even at the extreme of 1-bit weights and activations (W1A1). Furthermore, the 4-bit weights and 4-bit activations model (W4A4) trained with QuEST outperforms the baseline BF16 model in terms of achieving lower training loss at a smaller model size (Pareto dominance).
read the caption
Figure 1: The scaling law induced by QuEST when training Llama-family models from 30 to 800M parameters on C4, with quantized weights and activations from 1 to 4 bits, in the 100 tokens/parameter regime (higher compression uses proportionally more data at fixed memory). QuEST allows for stable training at 1-bit weights and activations (W1A1), and the QuEST W4A4 model is Pareto-dominant relative to BF16, with lower loss at lower size.

$P$	1	2	3	4	8	16
$\text{eff}(P)$	0.02	0.16	0.43	0.70	1.02	1.00

🔼 This table presents the fitted scaling law’s ’effective parameter’ multipliers for different numerical precisions (P). The effective parameter count is a metric that takes into account the impact of precision on model size and performance, offering a way to compare models of different architectures, sizes, and precisions under the same performance constraints. It shows how many parameters of a full-precision model are effectively being used when training with lower precisions, providing insights into the trade-offs between precision, compute, and model size.
read the caption
Table 1: Fitted scaling-law “effective parameter” multipliers.

In-depth insights
#

QuEST’s Novel QAT
#

QuEST introduces a novel approach to Quantization-Aware Training (QAT) for large language models (LLMs). Its key innovation lies in a trust gradient estimator that directly minimizes the error between the quantized and full-precision gradients. This contrasts with previous methods that primarily relied on the Straight-Through Estimator (STE), often leading to instability and inaccurate gradient estimations. Hadamard normalization is cleverly incorporated to improve the accuracy of quantization by making the data distribution closer to Gaussian, which is vital for optimal fitting. The method achieves Pareto-competitive results with FP16, demonstrating improved accuracy at lower model sizes, and enables stable training with extremely low-bit (even 1-bit) weights and activations, pushing the boundaries of current QAT capabilities.

Hadamard Transform
#

The research paper utilizes the Hadamard Transform as a pre-processing step before Gaussian fitting in their quantization method, QuEST. This is a crucial innovation, distinguishing it from previous QAT methods that relied on learned normalization. By applying the Hadamard Transform, the data’s distribution is shaped to better approximate a Gaussian distribution, improving the accuracy of subsequent quantization. This technique makes the subsequent MSE-optimal quantization more effective, reducing quantization errors and thereby improving gradient estimations during backpropagation. The authors suggest that the orthogonality and fast computation of the Hadamard Transform are key benefits, making their method more efficient than other methods. The transform facilitates stable training, especially at very low bit-widths such as 1-bit, by mitigating the impact of outliers. This is a significant advancement that contributes to QuEST’s superior performance and ability to achieve a Pareto-optimal frontier in low precision training.

Trust Gradient Estimator
#

The core idea behind the “Trust Gradient Estimator” is to improve the accuracy of gradient estimation during quantization-aware training (QAT) by reducing the impact of large quantization errors. Standard QAT methods often rely on the Straight-Through Estimator (STE), which can lead to significant inaccuracies, especially when quantization errors are substantial. The trust estimator addresses this by explicitly minimizing the difference between the true, full-precision gradient and the noisy gradient calculated from quantized values. It achieves this by assigning a “trust score” to each gradient component, based on its corresponding quantization error. Components with small errors are given high trust, while components with large errors (outliers) receive low trust, thus reducing their influence on the final gradient update. This approach is particularly effective at low bit-widths where quantization errors tend to be larger. The use of a Hadamard transform further enhances the estimator’s performance by improving the distribution of weights and activations before quantization, ultimately leading to more stable and accurate training.

Optimal Precision Frontier
#

The concept of “Optimal Precision Frontier” in the context of large language model (LLM) training centers on finding the sweet spot between model accuracy and computational efficiency. It’s a Pareto-optimal frontier, where increasing precision beyond a certain point yields diminishing returns in accuracy improvements, while incurring significantly higher computational costs. The research likely investigates how different quantization techniques impact this frontier, aiming to identify the minimum precision (bit-width) for weights and activations that maintains competitive accuracy while minimizing resource consumption. This involves analyzing the relationship between bit-width, model size, and training data, ultimately determining the optimal balance. Finding this frontier is crucial for deploying LLMs efficiently in resource-constrained environments.

GPU Kernel Enhancements
#

Optimizing GPU performance for quantized large language models (LLMs) is crucial for efficient inference. GPU kernel enhancements are essential in this context, focusing on accelerating computationally intensive operations like matrix multiplication with low-precision arithmetic (e.g., INT4). The paper likely details custom kernel implementations, potentially leveraging libraries such as CUTLASS, to handle the unique data formats and quantization schemes employed. Efficient Hadamard Transform kernels are also vital, given their use in the proposed QuEST method. The optimization strategies probably include techniques for memory access optimization, exploiting data parallelism, and minimizing unnecessary data transfers to maximize throughput. Performance gains are likely demonstrated through benchmarks comparing the custom kernels with standard implementations, highlighting improvements in speed and energy efficiency. The fusion of multiple operations into a single kernel is also a critical aspect, minimizing kernel launch overheads. The overall goal is to bridge the gap between computational support and achievable accuracy, enabling practical deployment of quantized LLMs on GPU hardware.

More visual insights
#

More on figures

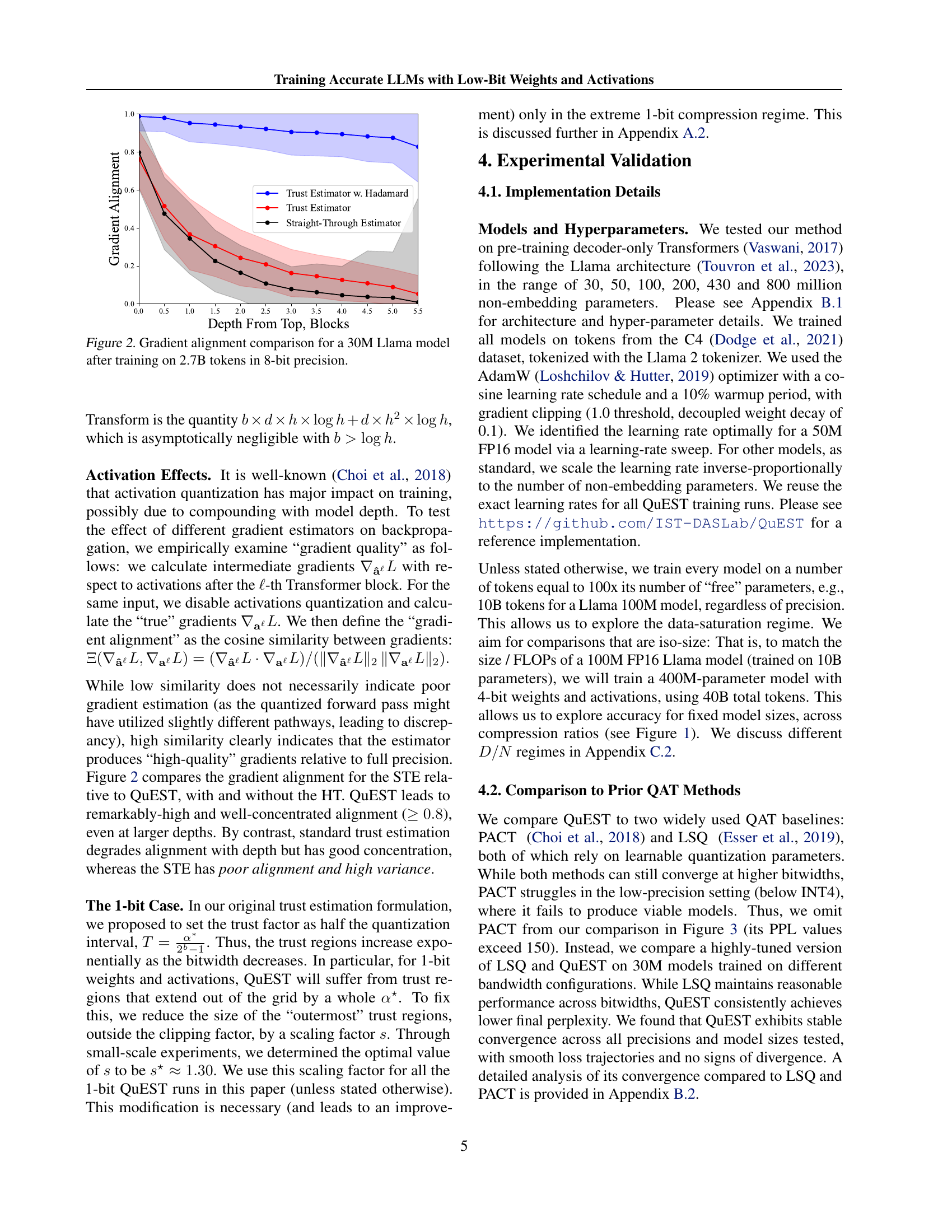
🔼 This figure displays the cosine similarity between gradients calculated with different methods (Straight-Through Estimator, trust estimation with and without Hadamard Transform) and the true full-precision gradients during the training of a 30M parameter Llama model. The training dataset comprised 2.7B tokens, and all gradients were calculated at 8-bit precision. The graph shows the alignment for each gradient estimator across different depths (Transformer blocks) in the model. This helps in visualizing how accurately each method estimates the gradient compared to the true value, providing insight into the effectiveness and stability of these methods during training.
read the caption
Figure 2: Gradient alignment comparison for a 30M Llama model after training on 2.7B tokens in 8-bit precision.

🔼 This figure compares the perplexity (a measure of how well a language model predicts a sequence of words) achieved by QuEST and LSQ, two different quantization-aware training (QAT) methods, across various bit-widths (the number of bits used to represent model weights and activations). The experiment uses a 30M parameter language model. The results show that QuEST consistently outperforms LSQ in terms of perplexity, and the improvement becomes more pronounced as the bit-width decreases (higher compression). This demonstrates QuEST’s effectiveness in achieving better accuracy at lower precisions compared to a tuned version of LSQ.
read the caption
Figure 3: Perplexity (PPL) across bit-widths with QuEST vs. a tuned variant of LSQ on a 30M model. QuEST leads to consistently lower PPL, with the advantage growing with compression.

🔼 This figure illustrates the efficiency of different numerical precisions and formats used in training large language models. The efficiency is measured by the ratio eff(P)/P, where eff(P) represents the effective parameter count for a given precision P, normalized by P itself. INT, FP, and INT+sparse represent integer, floating-point, and integer with sparsity formats, respectively. The higher the ratio, the more efficient the representation. The results indicate that INT4 (4-bit integer) offers the highest efficiency among hardware-supported formats, showing its potential advantage in training large language models.
read the caption
Figure 4: Illustration of the efficiency factors eff⁢(P)/Peff𝑃𝑃\text{eff}(P)/Peff ( italic_P ) / italic_P, arising from our analysis, for different numerical precisions P𝑃Pitalic_P and formats (INT, FP, INT+sparse). Higher is better. INT4 appears to have the highest efficiency among hardware-supported formats.

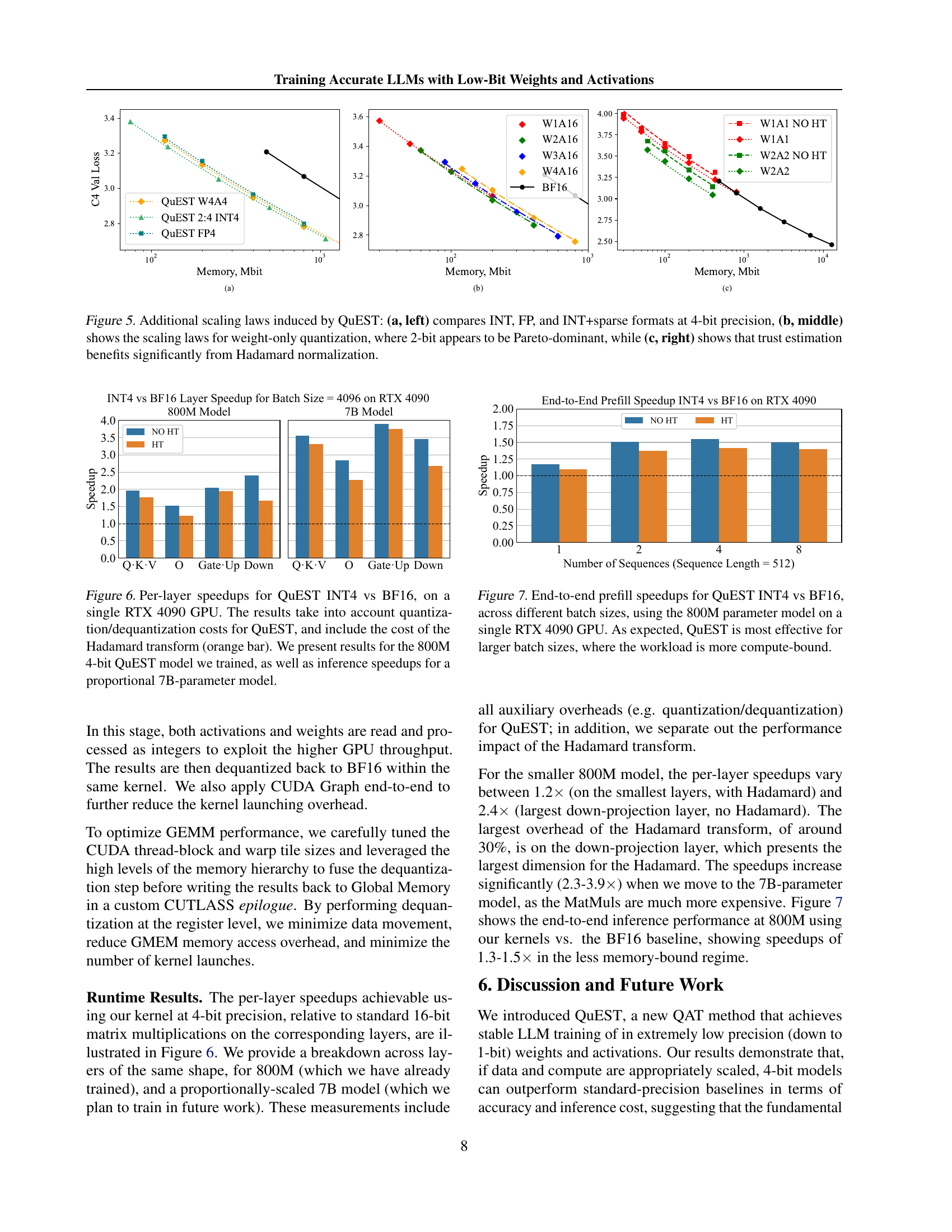
🔼 Figure 5 presents three subfigures illustrating different aspects of QuEST’s performance at 4-bit precision. Subfigure (a) compares the performance of three different quantization formats: INT (integer), FP (floating point), and INT+sparse (integer with sparsity). Subfigure (b) shows the scaling laws for weight-only quantization and demonstrates that 2-bit precision achieves Pareto-dominance. Subfigure (c) highlights the positive impact of Hadamard normalization on the trust estimation method used in QuEST.
read the caption
Figure 5: Additional scaling laws induced by QuEST: (a, left) compares INT, FP, and INT+sparse formats at 4-bit precision, (b, middle) shows the scaling laws for weight-only quantization, where 2-bit appears to be Pareto-dominant, while (c, right) shows that trust estimation benefits significantly from Hadamard normalization.

🔼 This figure displays the per-layer speedup achieved by using QuEST INT4 compared to BF16 on a single RTX 4090 GPU. The speedup is calculated considering the costs associated with quantization and dequantization in QuEST, and also factors in the computational overhead of the Hadamard Transform (represented by the orange bars). Results are shown for both an 800M parameter 4-bit QuEST model and a proportionally larger 7B-parameter model to demonstrate scalability.
read the caption
Figure 6: Per-layer speedups for QuEST INT4 vs BF16, on a single RTX 4090 GPU. The results take into account quantization/dequantization costs for QuEST, and include the cost of the Hadamard transform (orange bar). We present results for the 800M 4-bit QuEST model we trained, as well as inference speedups for a proportional 7B-parameter model.

🔼 This figure displays the end-to-end speedup achieved by using QuEST INT4 compared to using BF16 for inference on an 800M parameter model. The experiment was conducted on a single RTX 4090 GPU, varying the batch size of the input sequences. The results demonstrate that QuEST INT4 offers more significant speedup as the batch size increases. This is expected because larger batch sizes make the computation more compute-bound, allowing QuEST’s optimized low-precision operations to show greater performance gains.
read the caption
Figure 7: End-to-end prefill speedups for QuEST INT4 vs BF16, across different batch sizes, using the 800M parameter model on a single RTX 4090 GPU. As expected, QuEST is most effective for larger batch sizes, where the workload is more compute-bound.

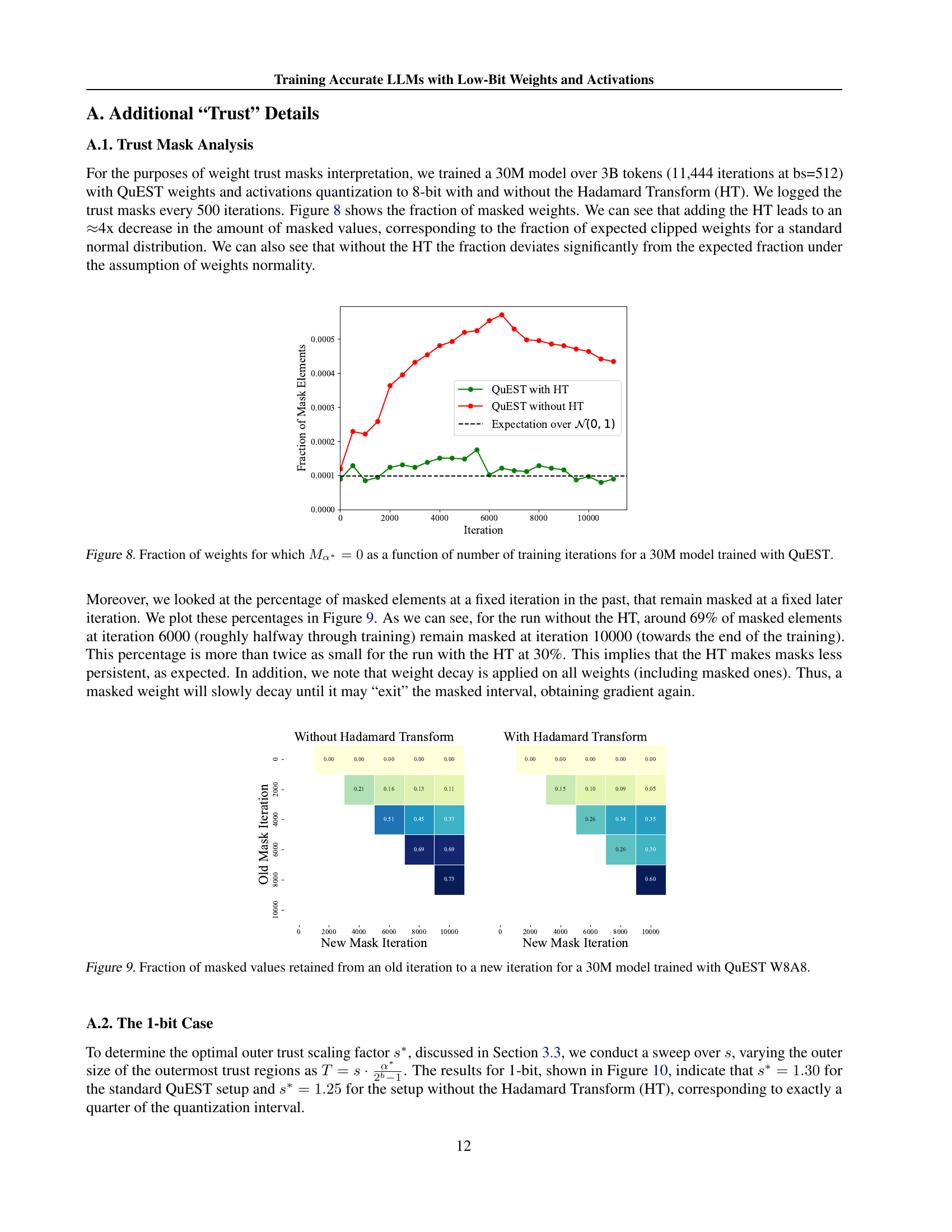
🔼 This figure shows the fraction of weights masked during training by the QuEST algorithm’s trust mask (Mα∗=0) over training iterations for a 30M parameter model. The trust mask is part of QuEST’s approach to estimate gradients accurately in low-precision training. A higher fraction indicates that a larger portion of the weights are considered unreliable for gradient updates during that iteration. Two lines are plotted, one showing the results with the Hadamard Transform (HT) and the other without. The HT is a component of QuEST, and the figure demonstrates its impact on the fraction of masked weights. The plot also includes a horizontal line showing the theoretically expected fraction of masked weights, assuming the weights follow a standard normal distribution. The comparison highlights how the Hadamard transform improves the approximation of the weight distribution to a normal distribution, leading to a more consistent trust mask.
read the caption
Figure 8: Fraction of weights for which Mα∗=0subscript𝑀superscript𝛼0M_{\alpha^{*}}=0italic_M start_POSTSUBSCRIPT italic_α start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT end_POSTSUBSCRIPT = 0 as a function of number of training iterations for a 30M model trained with QuEST.

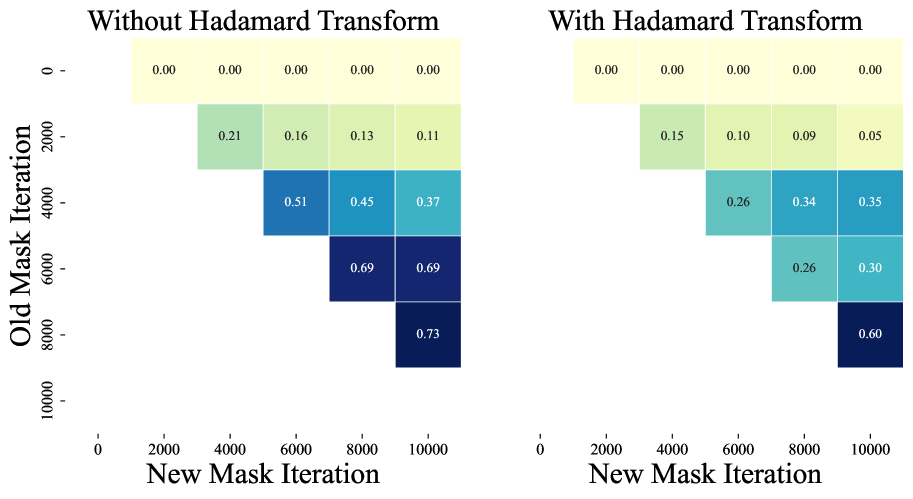
🔼 This figure visualizes the persistence of the trust mask in QuEST’s training process for a 30M parameter model using 8-bit weights and activations. It displays the percentage of masked values that remain masked from a previous iteration (old mask iteration) to a subsequent iteration (new mask iteration). The figure compares the mask persistence with and without using the Hadamard Transform (HT), demonstrating that the HT makes the masks significantly less persistent.
read the caption
Figure 9: Fraction of masked values retained from an old iteration to a new iteration for a 30M model trained with QuEST W8A8.

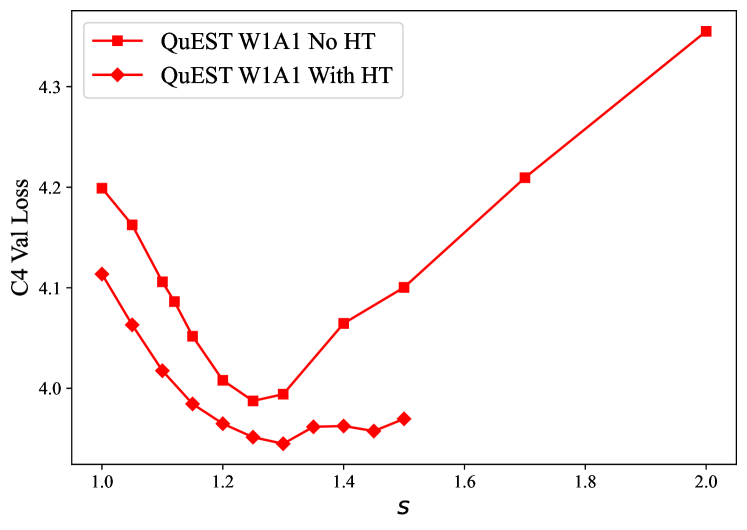
🔼 This figure illustrates how the performance of the QuEST model varies with changes to the outer trust scaling factor (represented as ’s’). The experiment was conducted during the pretraining phase of a 30M parameter model. The x-axis likely shows different values of ’s’, and the y-axis likely shows a performance metric, potentially validation loss, reflecting the model’s performance for each ’s’ value. The graph helps determine the optimal ’s’ value that balances accuracy and stability during training.
read the caption
Figure 10: Performance of QuEST as a function of the outer trust scaling factor s𝑠sitalic_s for a 30M model pretraining.

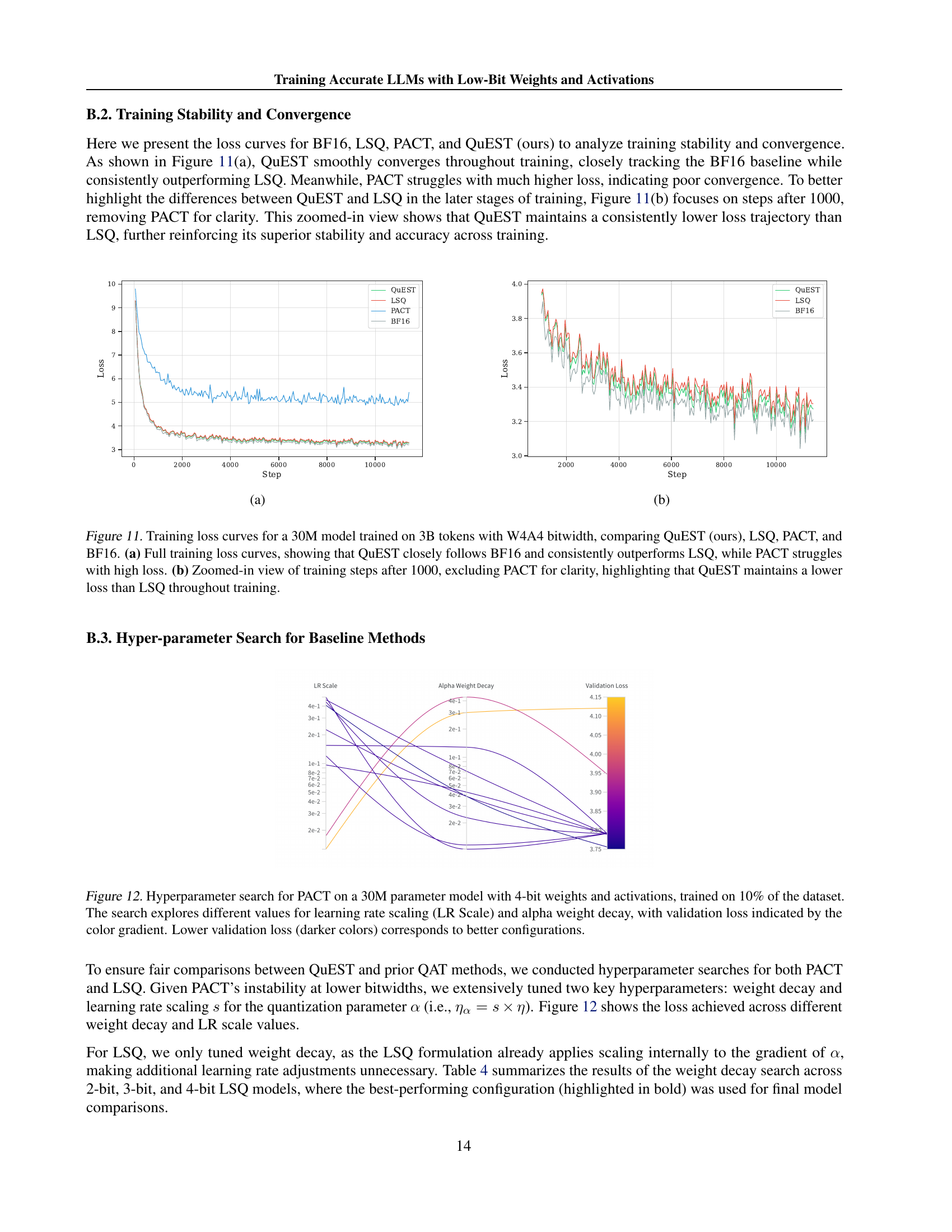
🔼 This figure displays the training loss curves for four different methods used to train a 30-million parameter language model on 3 billion tokens. The methods compared are QuEST, LSQ, PACT, and the baseline BF16 training. The graph in (a) shows the full training progression, revealing that QuEST’s loss curve closely mirrors the baseline BF16 method while consistently outperforming the other methods. PACT demonstrates poor convergence and high loss values. The graph in (b) provides a zoomed-in view of the loss curves after the first 1000 training steps. This view focuses on the comparison between QuEST and LSQ, illustrating QuEST’s consistent superiority in maintaining a lower training loss.
read the caption
Figure 11: Training loss curves for a 30M model trained on 3B tokens with W4A4 bitwidth, comparing QuEST (ours), LSQ, PACT, and BF16. (a) Full training loss curves, showing that QuEST closely follows BF16 and consistently outperforms LSQ, while PACT struggles with high loss. (b) Zoomed-in view of training steps after 1000, excluding PACT for clarity, highlighting that QuEST maintains a lower loss than LSQ throughout training.

🔼 This figure displays the results of a hyperparameter search performed for the PACT (Parameterized Clipping Activation) method. The goal was to find optimal settings for a 30-million parameter model using 4-bit weights and activations. The model was trained on only 10% of the complete dataset. The search space included different values for ’learning rate scaling’ and ‘alpha weight decay’. The validation loss achieved is visualized using a color gradient, where darker colors represent lower validation loss and therefore better model performance. This heatmap allows for the quick identification of the best hyperparameter combination for this specific model and setting.
read the caption
Figure 12: Hyperparameter search for PACT on a 30M parameter model with 4-bit weights and activations, trained on 10% of the dataset. The search explores different values for learning rate scaling (LR Scale) and alpha weight decay, with validation loss indicated by the color gradient. Lower validation loss (darker colors) corresponds to better configurations.

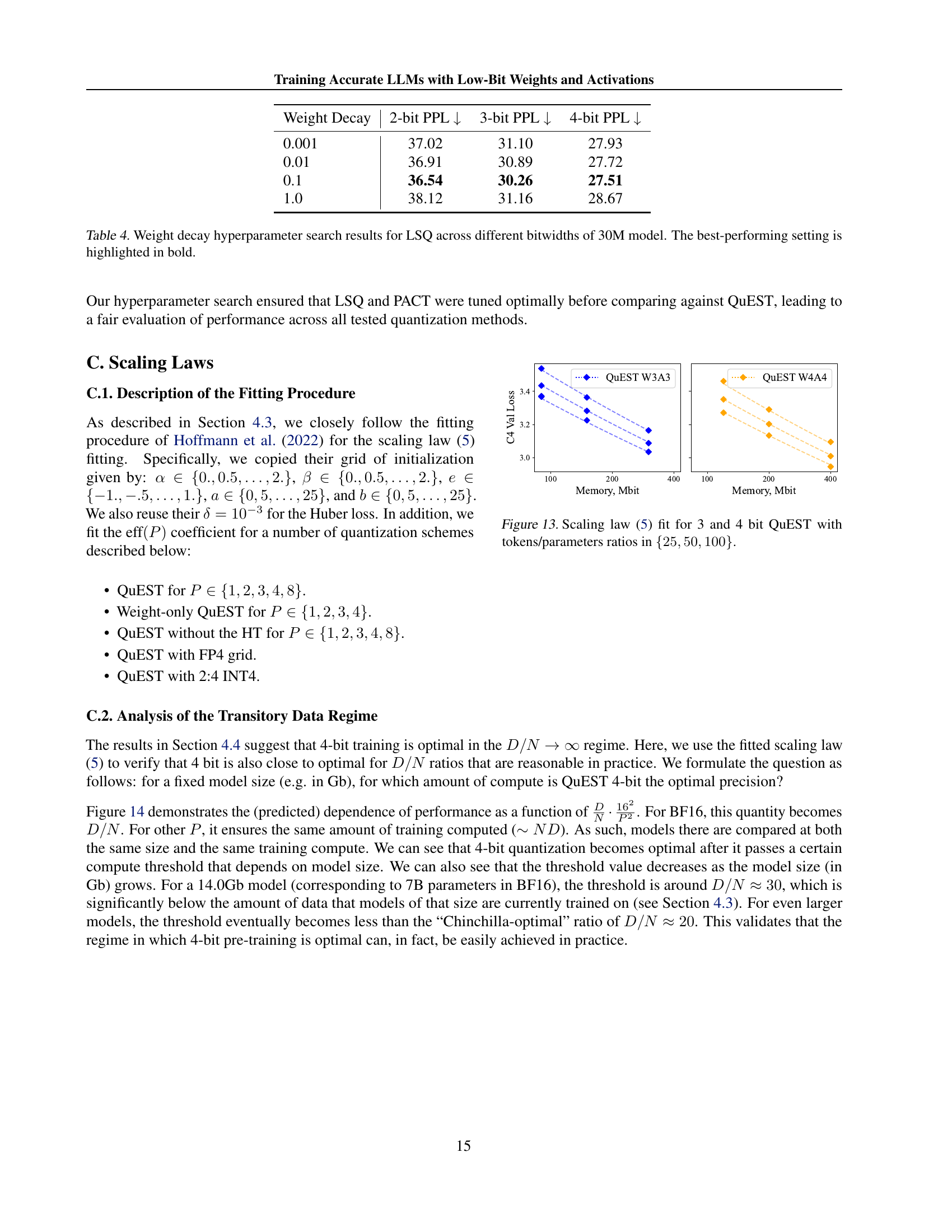
🔼 This figure displays the results of fitting the scaling law model (Equation 5 from the paper) to data obtained from training 3-bit and 4-bit models using the QuEST method. The x-axis represents model size in Megabits, and the y-axis represents the validation loss on the C4 dataset. Multiple lines show the results for different ratios of tokens to parameters (25, 50, and 100), illustrating how the relationship between model size and loss changes with varying data-model scaling regimes.
read the caption
Figure 13: Scaling law (5) fit for 3 and 4 bit QuEST with tokens/parameters ratios in {25,50,100}2550100\{25,50,100\}{ 25 , 50 , 100 }.

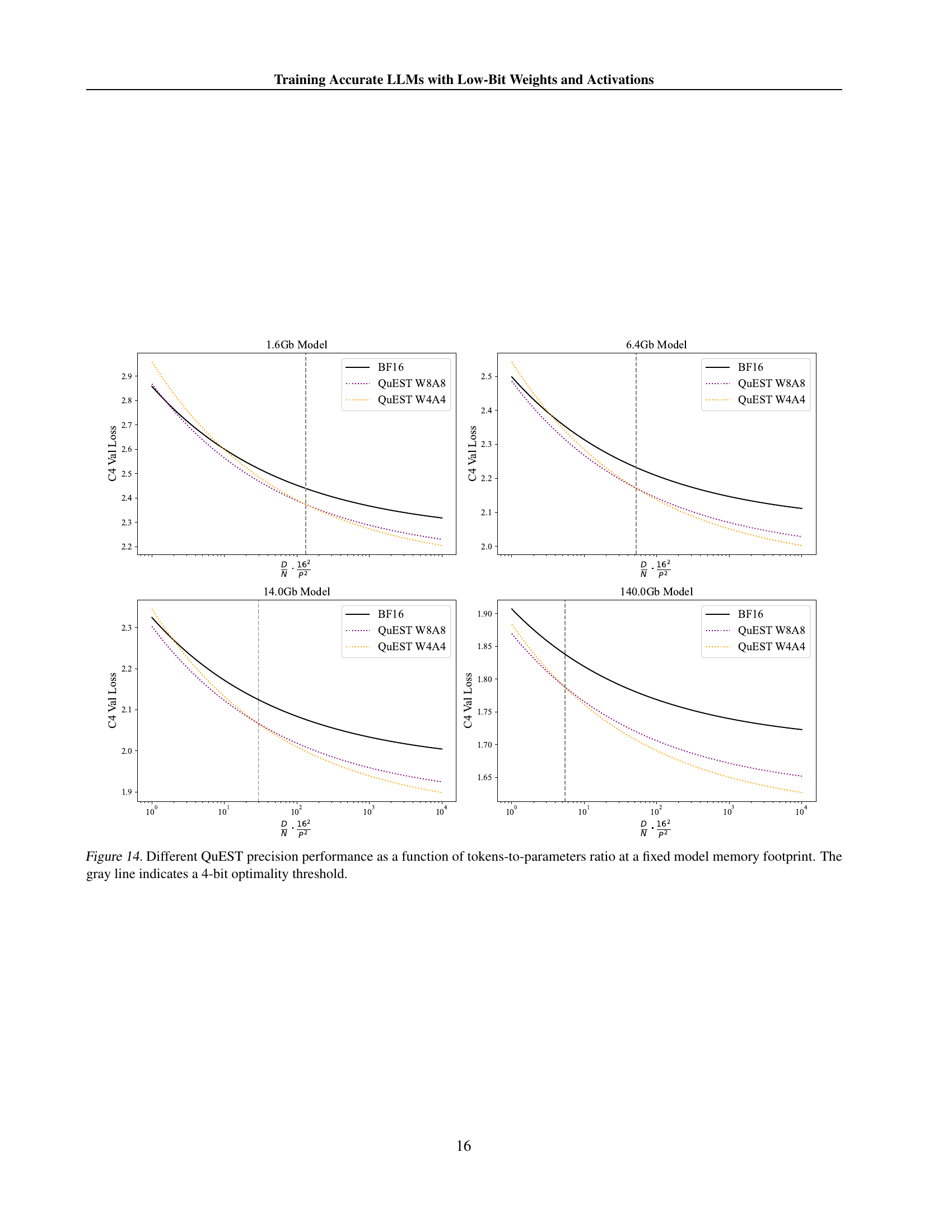
🔼 This figure displays the performance of QuEST at various precision levels (different bit-widths for weights and activations) in relation to the ratio of training tokens to model parameters. The key takeaway is that, while maintaining a constant model size (memory footprint), the optimal precision shifts depending on the amount of training data used. The graph shows how the loss (a measure of model performance) changes as this token-to-parameter ratio increases. A gray line is included as a visual reference to show where 4-bit precision becomes optimal.
read the caption
Figure 14: Different QuEST precision performance as a function of tokens-to-parameters ratio at a fixed model memory footprint. The gray line indicates a 4-bit optimality threshold.

Model	HellaSWAG Accuracy (%) ↑
BF16 (800M, 80B tokens)	39.52
QuEST 4-bit (800M, 80B tokens)	39.22

Model size	30M	50M	100M	200M	430M	800M
Num. Blocks	6	7	8	10	13	16
Hidden Size	640	768	1024	1280	1664	2048
Num. Attn. Heads	5	6	8	10	13	16
Learning Rate	0.0012	0.0012	0.0006	0.0003	0.00015	0.000075
Num. Tokens	3B	5B	10B	20B	43B	80B

Weight Decay	2-bit PPL ↓	3-bit PPL ↓	4-bit PPL ↓
0.001	37.02	31.10	27.93
0.01	36.91	30.89	27.72
0.1	36.54	30.26	27.51
1.0	38.12	31.16	28.67

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

QuEST’s Novel QAT#

Hadamard Transform#

Trust Gradient Estimator#

Optimal Precision Frontier#

GPU Kernel Enhancements#

More visual insights#

Full paper#