TL;DR#
Large language models (LLMs) often struggle with long-term planning and exploration during reinforcement learning (RL) fine-tuning. A common approach to mitigate this involves a KL penalty, which prevents the model from deviating too far from its pre-trained state. However, this can hinder the discovery of novel solutions. This paper focuses on the challenge of exploration in LLMs, especially when fine-tuning for complex tasks involving a distribution shift between pre-training and RL phases. The researchers examine how varying pre-training affects the exploration dynamics in a simple arithmetic task and find that pre-trained models tend to struggle with novel problem instances.
This research introduces a modified KL penalty that encourages exploration by prioritizing critical tokens — words or symbols that heavily influence the final outcome. Experiments on an arithmetic task demonstrate that this modified KL penalty significantly improves RL fine-tuning efficiency. The paper’s findings suggest that focusing exploration efforts on these key decision points, rather than uniformly penalizing divergence from the pre-trained model, is a more effective way to enhance the learning process. The proposed approach leads to better generalization and improved performance on unseen data, offering a valuable strategy for training LLMs capable of handling complex tasks.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the critical challenge of exploration in reinforcement learning for large language models. By identifying and prioritizing exploration on crucial tokens, it significantly improves the efficiency of RL fine-tuning. This work opens new avenues for research into efficient exploration strategies in LLM training and has implications for various downstream applications.
Visual Insights#

🔼 Figure 1 illustrates an arithmetic addition task given to a language model. The model, pre-trained on numbers with up to three digits, is shown attempting to add two four-digit numbers. The process is broken down step-by-step using a ‘scratchpad’ method, where intermediate calculations are displayed. Key tokens (‘critical tokens’) in the process, highlighted in the figure, represent decision points where the model is particularly prone to error. These errors stem from the model’s tendency to treat the four-digit numbers as if they were shorter, a behavior rooted in its pre-training on shorter numbers. The figure demonstrates the model’s struggle with out-of-distribution inputs and highlights where an improved exploration strategy is needed.
read the caption
Figure 1: Illustration of the addition task with scratchpad, for a model pre-trained on numbers up to 3 digits. The highlighted critical tokens are decision points where the model tends to make mistakes, mainly because it is tempted to process the number as if it were shorter. This occurs when the model is faced with a number that is longer than those encountered during the pre-training stage (here, 4 digits instead of 3).
| critical | non-critical (min.) | |
| -0.33 0.01 | 0.0012 0.0001 | |
| -0.21 0.18 | 0.0002 0.0001 | |
| -0.13 0.04 | 0.0004 0.0001 |
🔼 This table compares the difference in certainty between critical and non-critical tokens in a language model’s predictions. The model’s certainty (ΔJθold(s)) is measured for each token, and the average difference between the token’s certainty and the average certainty of other tokens in the sequence is calculated over 50 generations. The results show that the model exhibits substantially higher uncertainty on critical tokens, highlighting their importance in the overall model’s decision making process.
read the caption
Table 1: Comparison of the quantity ΔJ^θold(s)Δsubscript^𝐽subscript𝜃old𝑠\Delta\widehat{J}_{\theta_{\text{old}}}(s)roman_Δ over^ start_ARG italic_J end_ARG start_POSTSUBSCRIPT italic_θ start_POSTSUBSCRIPT old end_POSTSUBSCRIPT end_POSTSUBSCRIPT ( italic_s ) for critical and non-critical tokens, averaged over 50 generations. This shows the model’s high level of uncertainty on critical tokens.
In-depth insights#
RL Exploration Boost#
Reinforcement learning (RL) in large language models (LLMs) often struggles with exploration, needing a balance between discovering novel solutions and maintaining existing capabilities. A critical aspect highlighted is the use of KL penalties to control the divergence from the pre-trained model, which can stifle exploration. The core idea behind an ‘RL Exploration Boost’ would be to enhance the exploration process, potentially by modifying or replacing the KL penalty. This could involve prioritizing exploration in areas where the model shows uncertainty or identifying and focusing on ‘critical tokens’—tokens with significant impact on the overall outcome, as done in the referenced paper. Prioritizing exploration on these critical tokens could improve sample efficiency and allow the model to more effectively learn from out-of-distribution examples, thus ultimately advancing the model’s ability to reach long-term goals. A successful exploration boost would require a nuanced approach to balance exploration with exploitation, preventing catastrophic forgetting and ensuring that the model retains fundamental pre-trained skills.
KL Penalty Override#
A hypothetical section titled “KL Penalty Override” in a reinforcement learning (RL) context for language models would likely explore modifying the standard KL divergence penalty to improve exploration during fine-tuning. The core idea revolves around selectively reducing or overriding the KL penalty for specific tokens or actions deemed critical. This approach is motivated by the observation that traditional KL penalties, while stabilizing training, can hinder the discovery of novel solutions by excessively constraining the model to the pre-trained policy. By identifying and prioritizing exploration on crucial tokens, the RL process can efficiently escape local optima and achieve better generalization. This approach might involve techniques like assigning weights or dynamic scaling factors to the KL penalty based on factors such as token importance, model uncertainty, or the novelty of predicted actions. The success of a “KL Penalty Override” strategy would largely hinge on its ability to effectively balance exploration and exploitation, ensuring that crucial improvements are not sacrificed for excessive deviation from the pre-trained model’s established capabilities.
Critical Tokens Role#
The concept of “Critical Tokens” in the context of large language model (LLM) fine-tuning highlights the disproportionate influence of specific tokens on the overall outcome of a task. These tokens, often located at decision points in a multi-step process (like arithmetic calculations), represent critical junctures where a small error can propagate and lead to a cascading failure. The paper’s focus on arithmetic problems allows precise identification and analysis of critical tokens, demonstrating their role in determining the success or failure of a model’s generalization to unseen data. This insight is crucial for optimizing reinforcement learning (RL) fine-tuning strategies, as exploring and correcting the model’s behavior around these critical tokens can significantly improve performance. By modifying the KL penalty to emphasize exploration on these tokens, the researchers demonstrate improved efficiency in RL fine-tuning, suggesting that addressing model uncertainty specifically at these crucial points yields significant gains compared to a global approach. Future research could explore the generality of “Critical Tokens” in different LLM tasks and the development of more sophisticated methods to detect and mitigate their influence.
Pre-training Effects#
Pre-training significantly impacts a language model’s ability to generalize and explore during reinforcement learning (RL) fine-tuning. Models trained on a broader range of input lengths demonstrate better performance on out-of-distribution tasks involving longer sequences. This suggests that sufficient pre-training helps the model develop a robust understanding of the underlying structure, enabling better generalization. However, excessive pre-training can hinder exploration in RL, as models become overly confident in their pre-trained knowledge and are less likely to deviate from established patterns. This highlights the need to strike a balance: enough pre-training to ensure foundational competence, yet not so much as to stifle the learning process during RL fine-tuning. The study’s findings on ‘critical tokens’ further underscore the importance of pre-training, indicating that pre-training’s influence extends beyond general capabilities and affects specific decision points crucial for successful task completion. A well-trained model can exploit pre-trained knowledge effectively for standard parts of a task, but exploring novel solutions during RL requires overcoming reliance on this pre-trained knowledge precisely at these critical moments.
Future Research#
Future research should broaden the scope beyond the arithmetic task, exploring diverse problem types and larger language models. Investigating the impact of the prioritized KL penalty on other RL tasks and different model architectures is crucial. A deeper investigation into the nature of critical tokens is needed, understanding their emergence across various tasks and models. This could involve developing better methods for identifying them automatically and potentially incorporating this knowledge directly into the training process. Quantifying the trade-off between exploration and exploitation more precisely is also important, especially in the context of the balance between preserving pre-trained capabilities and promoting the discovery of novel solutions. Finally, future work should explore alternative RL algorithms to determine if the prioritized KL penalty’s effectiveness generalizes or if certain algorithms are inherently better suited for this type of targeted exploration.
More visual insights#
More on figures

🔼 This figure displays the accuracy of models trained on addition tasks with varying input digit lengths. Four different models were pre-trained on numbers with up to 7, 9, 11, and 13 digits, respectively. The graph then shows their accuracy on addition tasks where the number of digits varies from N+1 to N+3 (N being the number of digits the model was originally trained on). The error bars represent the 95% confidence interval, and more detailed data is available in Appendix D.1.
read the caption
Figure 2: Model accuracy on addition tasks for models trained on numbers up to digit lengths N=7,9,11,13𝑁791113N=7,9,11,13italic_N = 7 , 9 , 11 , 13. Results are shown for varying digit evaluation. Error bars indicate 95% confidence intervals. Full detailed results are provided in Appendix D.1.

🔼 This figure displays the learning curves for multiple language models. Each model was initially pre-trained on an arithmetic task involving numbers up to a certain digit length, denoted as N. Subsequently, these pre-trained models underwent fine-tuning using reinforcement learning (RL) on a similar task, but with numbers having two digits more (N+2). The graph illustrates the models’ learning progress over multiple training episodes, demonstrating how their accuracy on the N+2 digit task improves with experience. Comparing the curves of models pre-trained on different N values reveals the impact of the initial pre-training stage on the subsequent RL fine-tuning performance.
read the caption
Figure 3: Learning curves of multiple models pre-trained up to N𝑁Nitalic_N, fine-tuned with RL on N+2𝑁2N+2italic_N + 2.

🔼 Figure 4 presents a comparative analysis of two learning curves generated during reinforcement learning (RL) fine-tuning of a language model on an arithmetic addition task. The top panel displays the learning curves, illustrating the model’s performance improvement over training episodes. The bottom panel focuses on the probability of accurate predictions for two specific ‘critical tokens’ (tokens significantly impacting overall accuracy). These tokens, identified earlier in the study, highlight areas of notable challenge for the model during this RL training process. The figure showcases how focusing on these specific tokens, particularly during RL fine-tuning, influences overall accuracy. More detailed analysis on additional critical tokens is available in Appendix D.2.
read the caption
Figure 4: Top: Learning curves of a model fine-tuned with RL on N+1=8 digits. Bottom: Probability of making the right prediction on two critical tokens. Results on more critical tokens are provided in Appendix D.2.

🔼 This figure shows two examples of addition tasks where the model failed due to errors on critical tokens. The model, pretrained on numbers up to 3 digits, makes an error on the penultimate digit in (a), and in (b), pretrained on numbers up to 5 digits, it incorrectly inserts a bracket instead of a comma before copying the sixth digit. The colored tokens represent the model’s certainty, with green indicating high certainty and red indicating low certainty. This highlights how crucial some tokens are for correct task completion and how low certainty on these tokens leads to incorrect answers.
read the caption
(a)

🔼 Figure 5(b) shows an example of a failed addition task where the model, pre-trained on numbers up to 5 digits, makes a mistake during the decomposition stage. Instead of correctly continuing the addition process, it prematurely closes the bracket, leading to an incorrect answer. The color-coding of the generated tokens indicates the model’s certainty, with green representing high certainty and red representing low certainty. This highlights the critical tokens that significantly affect the final result.
read the caption
(b)

🔼 This figure displays an example of an addition task where the model is given two numbers with 11 and 10 digits, respectively, to add. The model uses a scratchpad to perform the calculation step by step. The color coding of the tokens indicates the model’s confidence level, with green indicating high confidence and red indicating low confidence. This example illustrates a scenario where the model makes errors due to low confidence in some critical tokens, which can affect the final result.
read the caption
(c)

🔼 This figure displays three examples of the model’s output when performing addition tasks involving numbers with one more digit than it was trained on (N+1 digits). Each token generated by the model is color-coded to represent its certainty: green indicates high certainty, and red indicates low certainty. The examples highlight the model’s struggles with longer numbers and showcase the emergence of ‘critical tokens’ (those with low certainty) which significantly impact the final result. The scratchpad notation used helps illustrate the step-by-step process of the model’s addition attempt.
read the caption
Figure 5: Output examples for addition tasks on N+1𝑁1N+1italic_N + 1 digit lengths (the model is faced with numbers one notch longer than those encountered in pre-training). Each generated token is colored according to its certainty. A green color is a maximal certainty, while a red color is a minimal certainty.

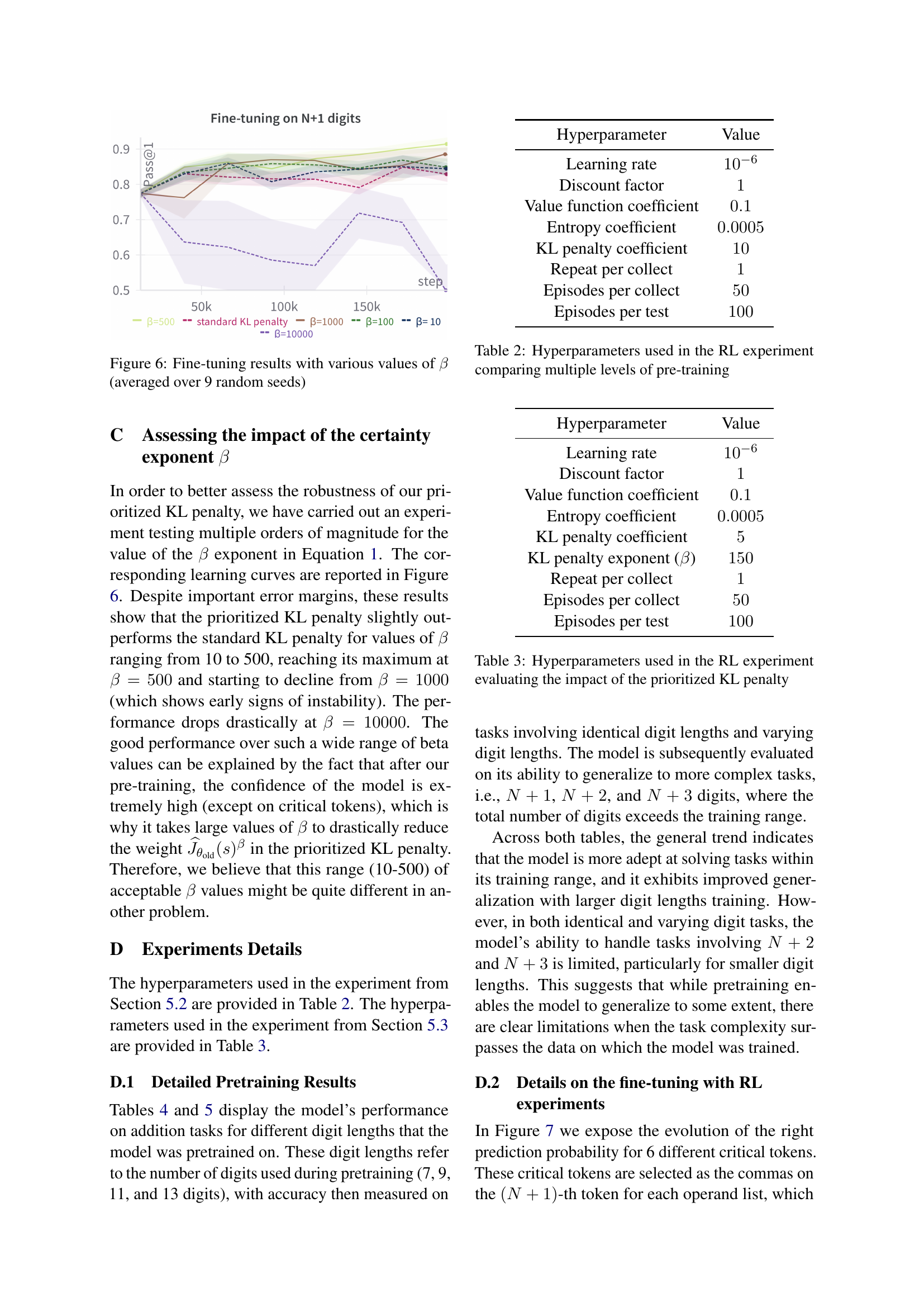
🔼 This figure displays the fine-tuning results obtained using the prioritized KL penalty with different values of beta (β). The y-axis represents the Pass@1 metric, indicating the model’s accuracy in achieving the correct answer. The x-axis shows the training steps. Multiple lines represent the results with varying beta values. The results are averaged over nine separate runs (random seeds), which helps in estimating the robustness and stability of the model’s performance under the different beta values used in the prioritized KL penalty.
read the caption
Figure 6: Fine-tuning results with various values of β𝛽\betaitalic_β (averaged over 9 random seeds)

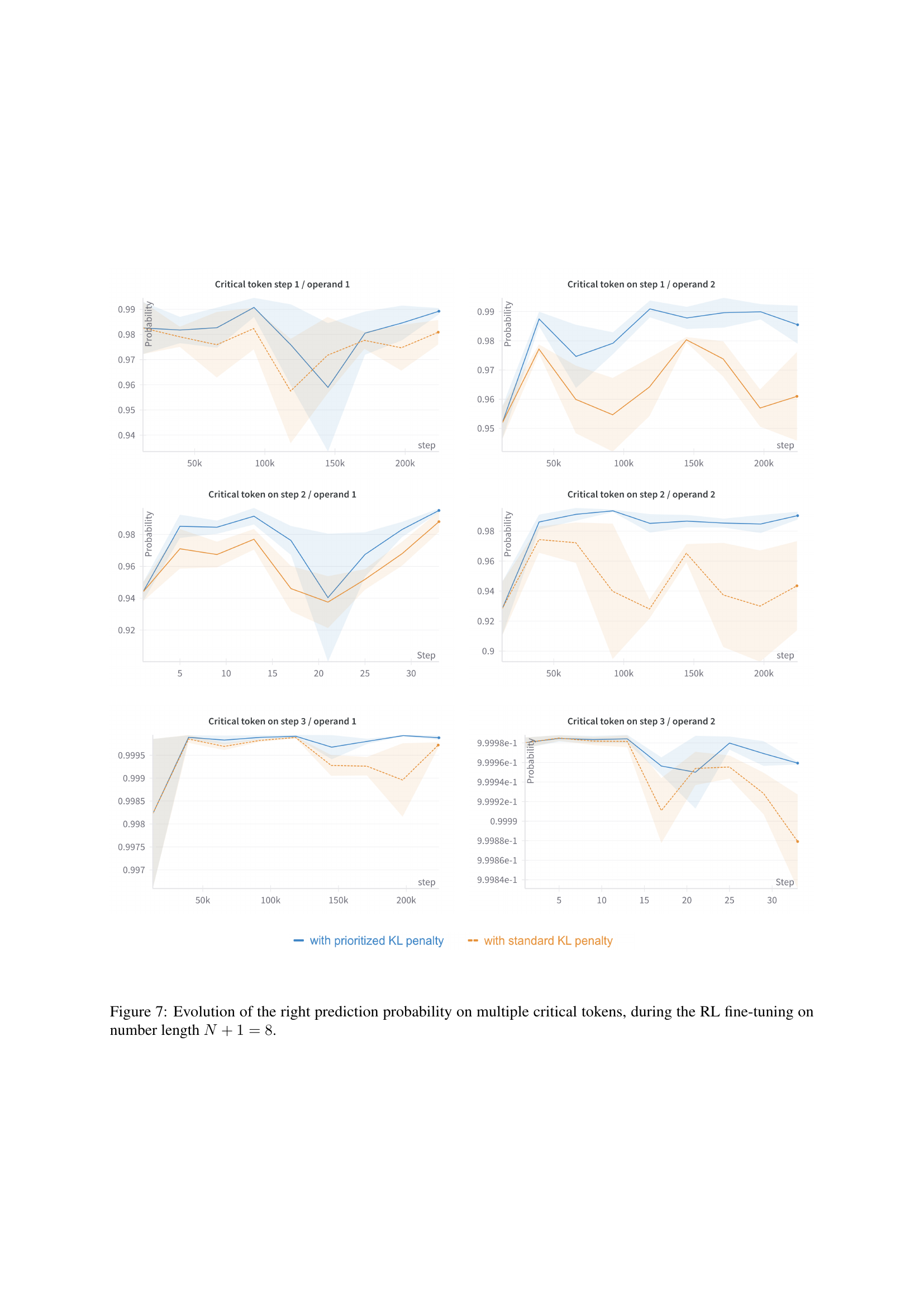
🔼 Figure 7 illustrates the evolution of the probability of making the correct prediction on six different critical tokens during the reinforcement learning (RL) fine-tuning process. The fine-tuning is performed on an arithmetic addition task, where the input numbers have N+1=8 digits. The graph plots the probability over the course of the RL training (number of steps), differentiating between the results obtained using the standard KL penalty and the prioritized KL penalty (introduced in the paper). Each line represents a specific critical token (comma positions in the scratchpad), highlighting how each method affects the model’s ability to learn to correctly predict these crucial points during the calculation.
read the caption
Figure 7: Evolution of the right prediction probability on multiple critical tokens, during the RL fine-tuning on number length N+1=8𝑁18N+1=8italic_N + 1 = 8.
More on tables
| Hyperparameter | Value |
| Learning rate | |
| Discount factor | |
| Value function coefficient | |
| Entropy coefficient | |
| KL penalty coefficient | |
| Repeat per collect | |
| Episodes per collect | |
| Episodes per test |
🔼 This table lists the hyperparameters used in the reinforcement learning (RL) experiment designed to compare the performance of language models pre-trained with varying levels of input data. The hyperparameters control the learning process, including the learning rate, discount factor, value function coefficient, entropy coefficient, KL penalty coefficient, the number of repetitions before collecting data, the number of episodes per data collection, and the number of episodes per test.
read the caption
Table 2: Hyperparameters used in the RL experiment comparing multiple levels of pre-training
| Hyperparameter | Value |
| Learning rate | |
| Discount factor | |
| Value function coefficient | |
| Entropy coefficient | |
| KL penalty coefficient | |
| KL penalty exponent () | |
| Repeat per collect | |
| Episodes per collect | |
| Episodes per test |
🔼 This table lists the hyperparameters used in a reinforcement learning (RL) experiment designed to assess the effectiveness of a modified KL penalty. The experiment specifically focuses on how this modified penalty, which prioritizes exploration on critical tokens, impacts the overall performance of a language model fine-tuned for an arithmetic task.
read the caption
Table 3: Hyperparameters used in the RL experiment evaluating the impact of the prioritized KL penalty
| Nb. of Digits | Accuracy | Accuracy | Accuracy | Accuracy |
| 7 | 98.9% 0.7% | 48.8% 3.0% | 0.0% 0.0% | 0.0% 0.0% |
| 9 | 96.4% 0.6% | 78.9% 2.4% | 0.5% 0.5% | 0.0% 0.0% |
| 11 | 91.2% 1.3% | 75.1% 2.7% | 30.7% 2.4% | 0.2% 0.3% |
| 13 | 93.0% 1.6% | 88.9% 2.1% | 67.7% 3.1% | 20.4% 2.4% |
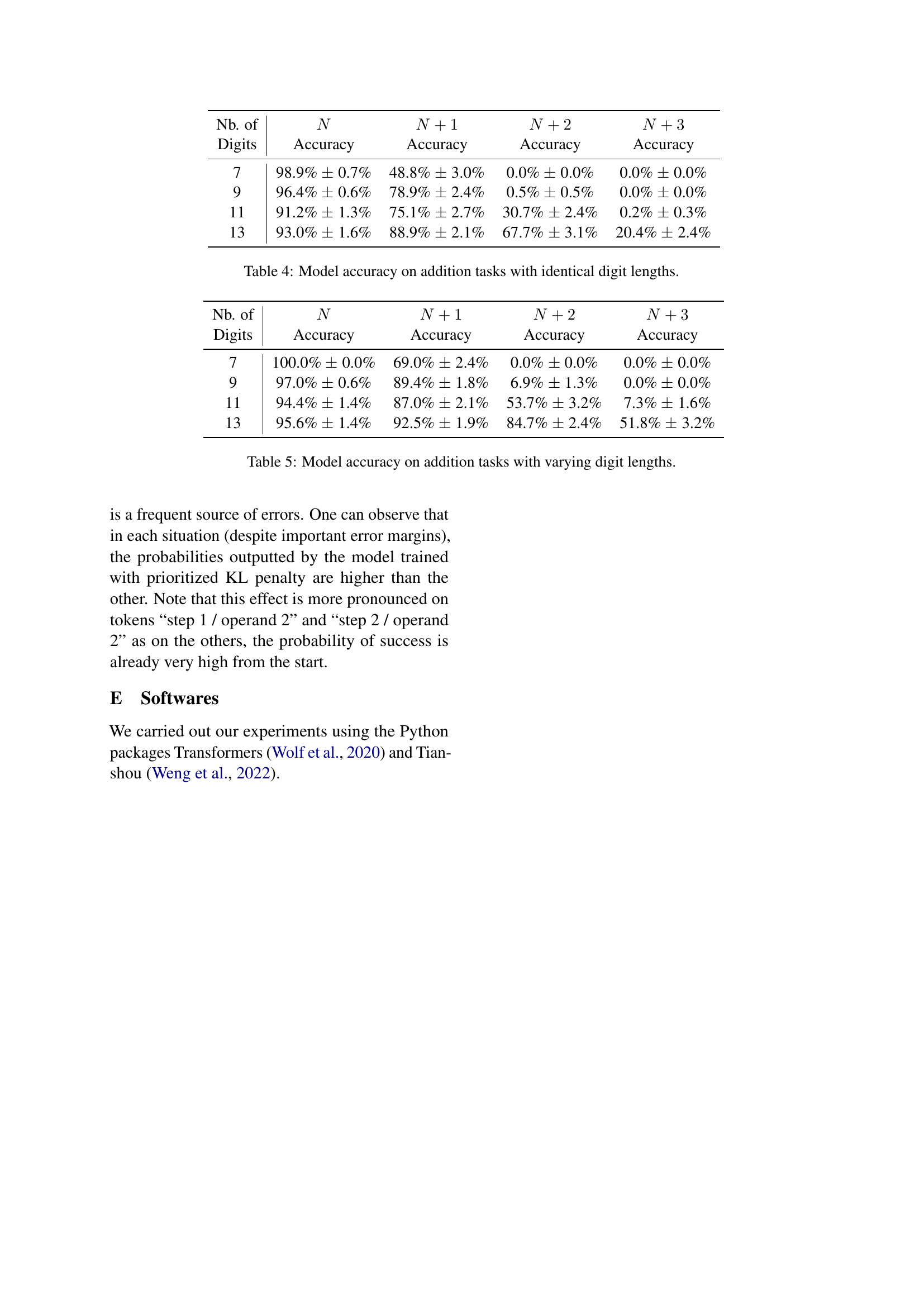
🔼 This table presents the model’s accuracy on addition tasks where both numbers have the same number of digits. The accuracy is shown for various lengths of digits (N), as well as for addition problems involving numbers with more digits than those seen during training (N+1, N+2, N+3). The results highlight the model’s ability to generalize to longer digit lengths and the impact of the pre-training phase on its ability to solve these addition problems.
read the caption
Table 4: Model accuracy on addition tasks with identical digit lengths.
| Nb. of Digits | Accuracy | Accuracy | Accuracy | Accuracy |
| 7 | 100.0% 0.0% | 69.0% 2.4% | 0.0% 0.0% | 0.0% 0.0% |
| 9 | 97.0% 0.6% | 89.4% 1.8% | 6.9% 1.3% | 0.0% 0.0% |
| 11 | 94.4% 1.4% | 87.0% 2.1% | 53.7% 3.2% | 7.3% 1.6% |
| 13 | 95.6% 1.4% | 92.5% 1.9% | 84.7% 2.4% | 51.8% 3.2% |
🔼 This table presents the model’s accuracy on arithmetic addition tasks where the number of digits in the two added numbers varies. The model was pre-trained on addition tasks with a specific maximum number of digits (indicated in the ‘Digits’ column). The table shows accuracy for addition tasks of different digit lengths, including tasks where the digit length matches the pre-training length (N), and tasks where one or both numbers have more digits (N+1, N+2, N+3). Results indicate the model’s ability to generalize to addition problems beyond its initial training.
read the caption
Table 5: Model accuracy on addition tasks with varying digit lengths.
Full paper#