TL;DR#
Training large language models (LLMs) is computationally expensive, and deploying them on resource-constrained devices requires model compression techniques like quantization. However, traditional quantization methods often lead to a significant trade-off between model accuracy and precision, especially at lower precision levels (e.g. int2). Practitioners typically use multiple models to balance accuracy and latency, increasing the complexity of deployment.
This research introduces Matryoshka Quantization (MatQuant), a novel method that addresses these limitations. MatQuant leverages the nested structure of integer data types to jointly optimize model weights across multiple precision levels (int8, int4, int2). This allows for extracting multiple accurate lower-precision models from a single trained model. Results show significant improvements in the accuracy of int2 models, outperforming standard int2 quantization techniques by up to 10%, while maintaining comparable accuracy at higher precisions. Additionally, MatQuant seamlessly extracts accurate models for intermediate precision levels without requiring separate training.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel quantization technique that significantly improves the accuracy of low-precision models, which is crucial for deploying large language models efficiently on resource-constrained devices. It addresses the challenge of needing multiple models with different quantization levels by enabling the training and maintenance of a single model. This also opens avenues for future research, particularly in exploring multi-scale training techniques and their application to other areas of deep learning.
Visual Insights#

🔼 This figure shows a multi-scale quantization training technique leveraging the nested structure of integer data types. Specifically, it illustrates how smaller bit-width integers (int4, int2) are nested within larger ones (int8). This nested structure is exploited to train a single model that can be efficiently served at different precision levels, addressing the challenge of needing multiple quantized models for different accuracy/latency trade-offs.
read the caption
(a)
| Data type | Method | Gemma-2 2B | Gemma-2 9B | Mistral 7B | |||
|---|---|---|---|---|---|---|---|
| OmniQuant | Task Avg. | log pplx. | Task Avg. | log pplx. | Task Avg. | log pplx. | |
| bfloat16 | |||||||
| int8 | Baseline | ||||||
| int4 | Sliced int8 | ||||||
| Baseline | |||||||
| int2 | Sliced int8 | ||||||
| Baseline | |||||||
| int6 | Sliced int8 | ||||||
| Baseline | |||||||
| int3 | Sliced int8 | ||||||
| Baseline | |||||||
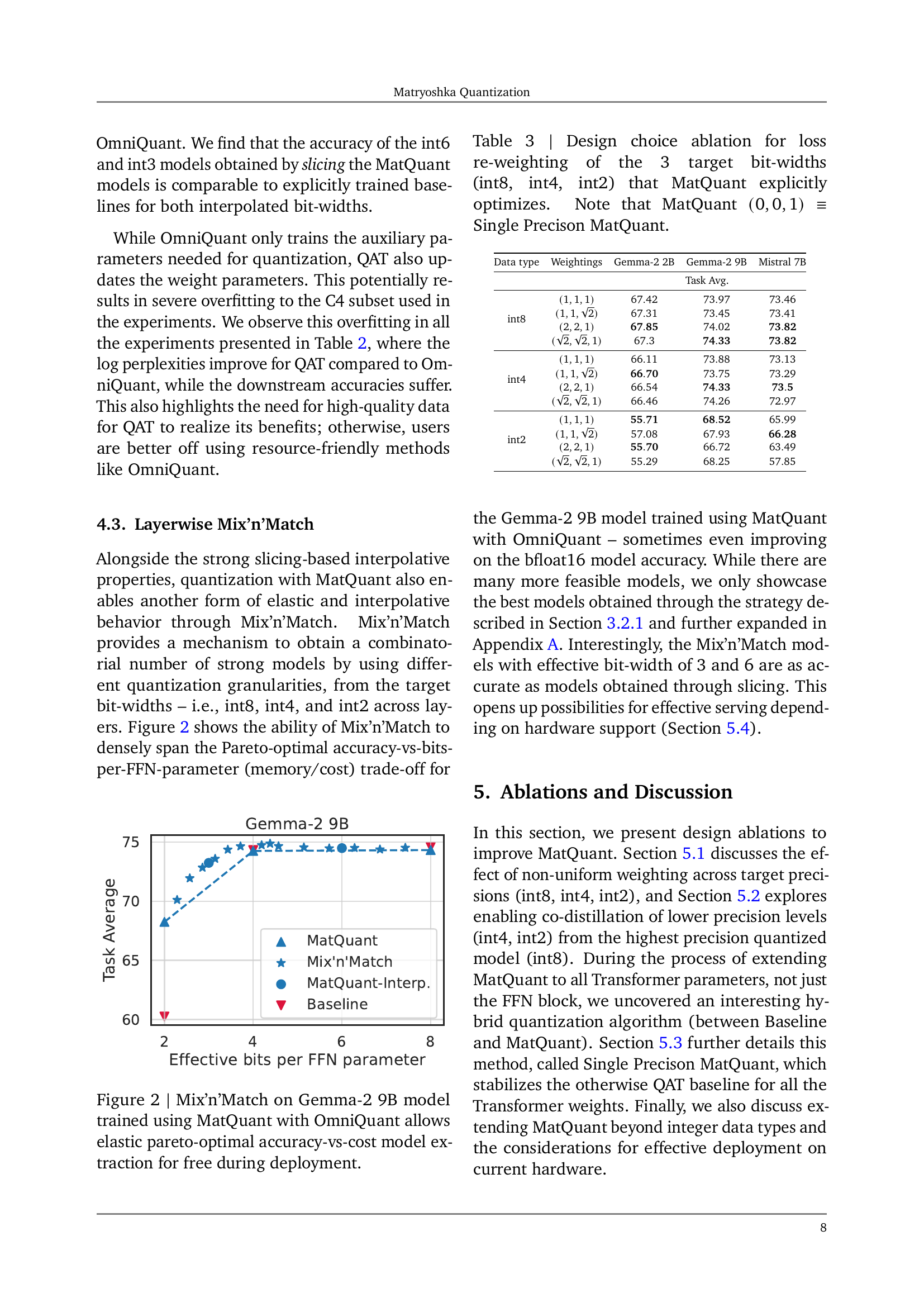
🔼 This table presents a comparison of the performance of Matryoshka Quantization (MatQuant) against baseline methods for quantizing the Gemma-2 (2B and 9B) and Mistral-7B LLMs. MatQuant is evaluated at various bit-widths (int8, int4, int2, int6, int3). The results show that MatQuant achieves comparable performance to the baselines for int8 and int4, but substantially improves accuracy for int2. Importantly, MatQuant’s multi-scale training allows for the extraction of int3 and int6 models with accuracy comparable to independently trained baselines, demonstrating its efficiency.
read the caption
Table 1: MatQuantMatQuant{\rm MatQuant}roman_MatQuant with OmniQuant across Gemma-2 2B, 9B and Mistral 7B models. MatQuantMatQuant{\rm MatQuant}roman_MatQuant performs on par with the baseline for int4 and int8 while significantly outperforming it for int2. Even the int3, int6 models obtained for free through interpolation from MatQuantMatQuant{\rm MatQuant}roman_MatQuant perform comparably to the explicitly trained baselines. Task Avg. is average accuracy on the evaluation tasks (↑↑\uparrow↑) while log pplx (perplexity) is computed on C4 validation set (↓↓\downarrow↓).
In-depth insights#
MatQuant: Multi-Scale#
MatQuant, a multi-scale quantization technique, presents a novel approach to model quantization by leveraging the nested structure of integer data types. Instead of training separate models for different precision levels (e.g., int8, int4, int2), MatQuant trains a single model that can be efficiently served at various precisions. This is achieved by jointly optimizing the model’s weights across multiple precisions. The inherent Matryoshka structure allows smaller bit-width integers to be nested within larger ones, enabling seamless extraction of lower-precision models from the trained model. This multi-scale approach results in significant improvements in accuracy, especially for low-precision quantization (int2), outperforming traditional methods by up to 10%. Further, MatQuant demonstrates adaptability through interpolation and Mix’n’Match strategies, offering flexibility in balancing accuracy and resource consumption. This work is of high significance as it addresses the trade-off between model accuracy and efficiency inherent in model quantization, offering a more versatile and computationally efficient approach to deploying large language models.
Int2 Accuracy Boost#
The research paper’s focus on achieving an ‘Int2 Accuracy Boost’ is a significant contribution to model quantization. Standard int2 quantization methods often suffer from substantial accuracy loss, making them impractical for many applications. The paper’s novel approach, likely involving a multi-scale training technique and/or innovative regularization, directly addresses this limitation. The reported 10% improvement over standard int2 methods is remarkable, showcasing a clear advancement in the field. This finding suggests that the proposed technique effectively mitigates the information loss inherent in lower-bit quantization. The method’s general-purpose nature, applicable across various models, further amplifies its significance, implying a potentially wide-ranging impact on resource-constrained deployments of large language models and other deep learning architectures. The success hinges on effectively harnessing the nested structure of integer data types to enable seamless extraction of multiple precision models. This breakthrough has important implications for model deployment, enabling a trade-off between accuracy and inference speed tailored to specific hardware constraints.
Mix’n’Match Quantization#
Mix’n’Match quantization, as a concept, offers a powerful approach to optimize model efficiency. By allowing different layers of a neural network to utilize varying quantization precisions, it dynamically balances accuracy and resource consumption. Instead of applying a uniform quantization scheme across the entire model, this technique strategically chooses the most appropriate precision for each layer based on its sensitivity to quantization. Layers requiring high accuracy retain higher precision (e.g., int8), while less critical layers can leverage lower precisions (e.g., int4 or int2) to significantly reduce computational costs and memory footprint. This adaptability makes Mix’n’Match particularly useful for deployment on hardware with diverse capabilities, allowing for customized optimization based on the specific resource constraints of the target platform. The ability to seamlessly combine various precisions is a key advantage, offering a more granular control over the model’s efficiency compared to uniform quantization. Furthermore, research into optimal strategies for layer-wise precision selection is an important area for future exploration, considering factors like layer importance, activation patterns, and computational demands. The flexibility and potential performance gains of Mix’n’Match quantization make it a promising area of research for improving the efficiency and deployment of deep learning models across various hardware platforms.
Interpolative Behavior#
The concept of “Interpolative Behavior” in the context of Matryoshka Quantization is a significant finding. It demonstrates that a model trained to optimize across multiple precision levels (e.g., int8, int4, int2) can be effectively used at intermediate precisions. Simply slicing the higher-precision model’s most significant bits to extract lower-precision versions yields surprisingly accurate results, comparable to models specifically trained at those intermediate levels. This is a crucial efficiency gain as it eliminates the need to train separate models for each desired precision. The nested structure of integer data types is leveraged here, showing that the knowledge acquired during multi-scale training is transferable and robust enough to provide good performance even when not explicitly trained for those precisions. This interpolative property significantly reduces the computational cost and storage requirements associated with model quantization. This characteristic of Matryoshka Quantization allows for flexible and cost-effective deployment, making it particularly attractive for resource-constrained environments where serving multiple models is impractical.
Future: FP Extension#
Extending Matryoshka Quantization (MatQuant) to floating-point (FP) numbers presents a significant challenge. Unlike integers, where slicing MSBs directly yields lower precision representations, FP numbers have an exponent and mantissa. Slicing the exponent results in exponentially increasing bucket sizes, disrupting the nested structure crucial to MatQuant’s multi-scale optimization. This makes achieving a seamless accuracy-cost tradeoff difficult as observed in integer quantization. Addressing this would require innovative techniques that handle the non-linear relationship between exponent and mantissa values during quantization. This might involve new loss functions or quantization schemes that preserve the accuracy of the exponent’s contribution. Successful FP extension of MatQuant could unlock its benefits for a wider range of hardware and model architectures, expanding its applicability beyond integer-based systems and making low-precision inference even more efficient and versatile.
More visual insights#
More on figures

🔼 MatQuant is a multi-scale quantization training technique that leverages the inherent nested structure of integer data types (int8, int4, int2). It allows training and maintaining just one model, which can then be served at different precision levels. The figure shows how the most significant bits (MSBs) of an int8-quantized weight can be directly sliced to yield an int4 or int2 model, demonstrating the nested Matryoshka structure.
read the caption
(a)

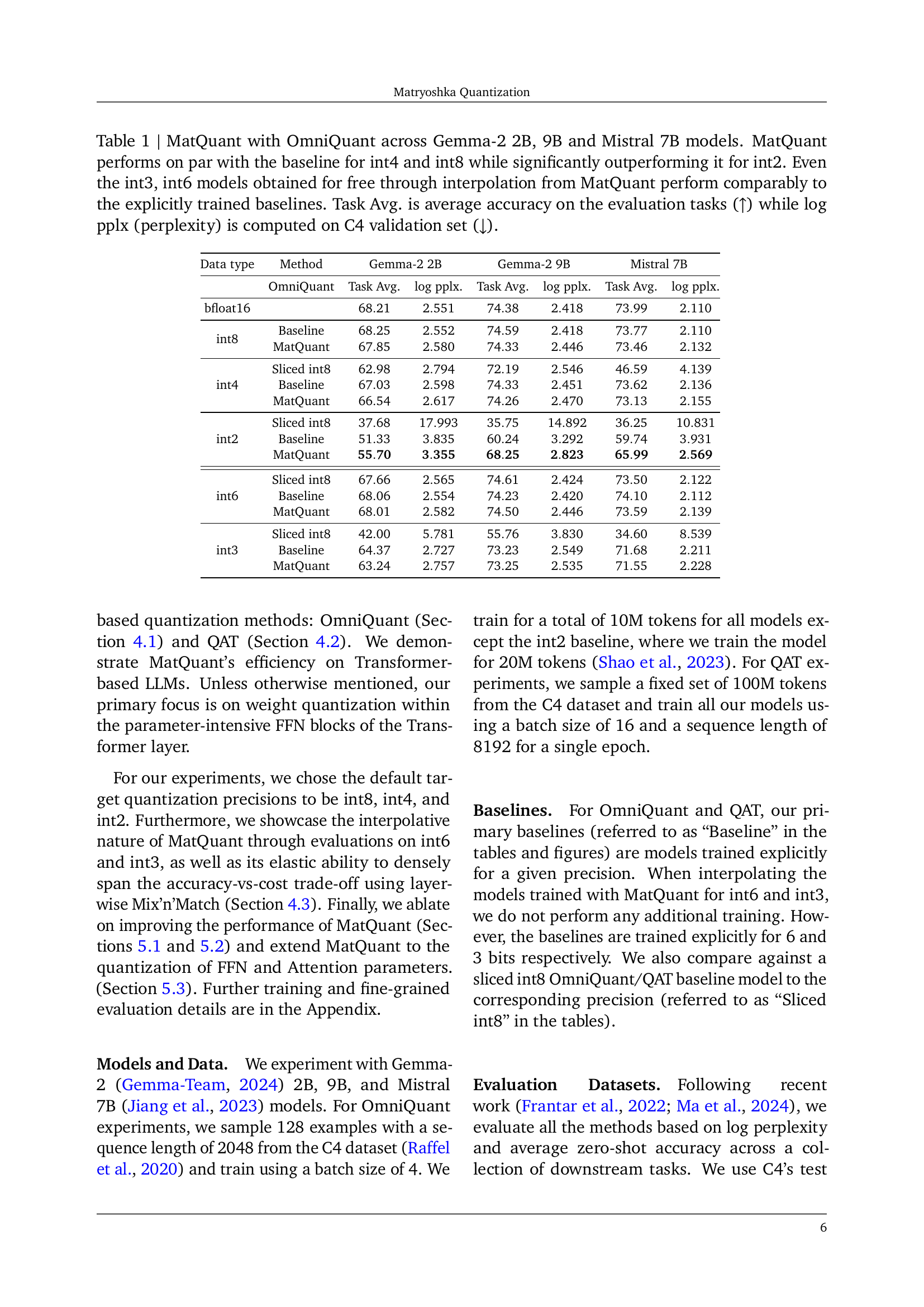
🔼 This figure shows the empirical gains achieved by Matryoshka Quantization (MatQuant) on downstream tasks compared to baseline methods. The x-axis represents the effective bits per feed-forward network (FFN) parameter, reflecting different quantization levels (int2, int4, int8). The y-axis shows the performance, measured as task average. MatQuant demonstrates a significant performance boost for int2 quantization, surpassing the accuracy of the baseline model by more than 8%. For int4 and int8, MatQuant’s performance is comparable to the baseline.
read the caption
(b)
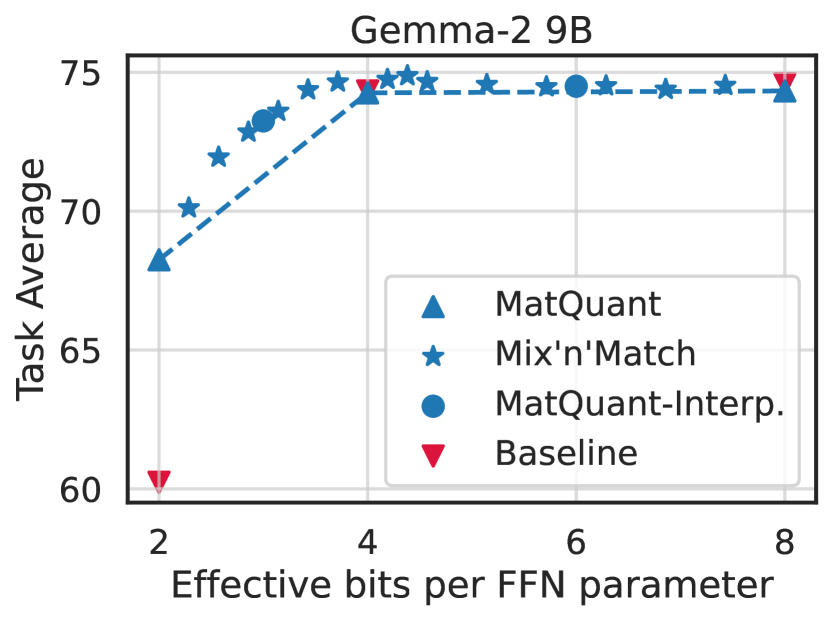
🔼 This figure shows the empirical gains achieved by Matryoshka Quantization (MatQuant) on downstream tasks compared to baseline methods for various bit-widths (int2, int4, int8). The graph highlights the significant improvement in accuracy, particularly for int2 models, demonstrating MatQuant’s effectiveness in achieving high accuracy at low precisions. The x-axis represents the effective bits per FFN parameter (a measure of model size and computational cost), while the y-axis represents the frequency.
read the caption
(b)
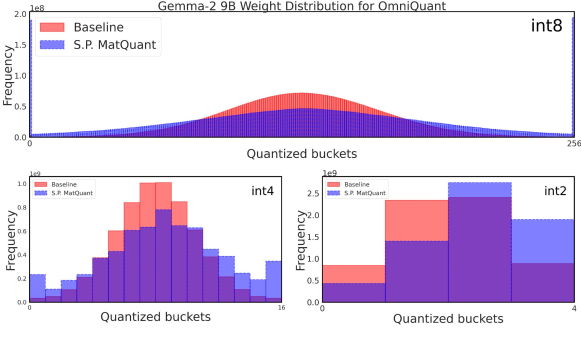
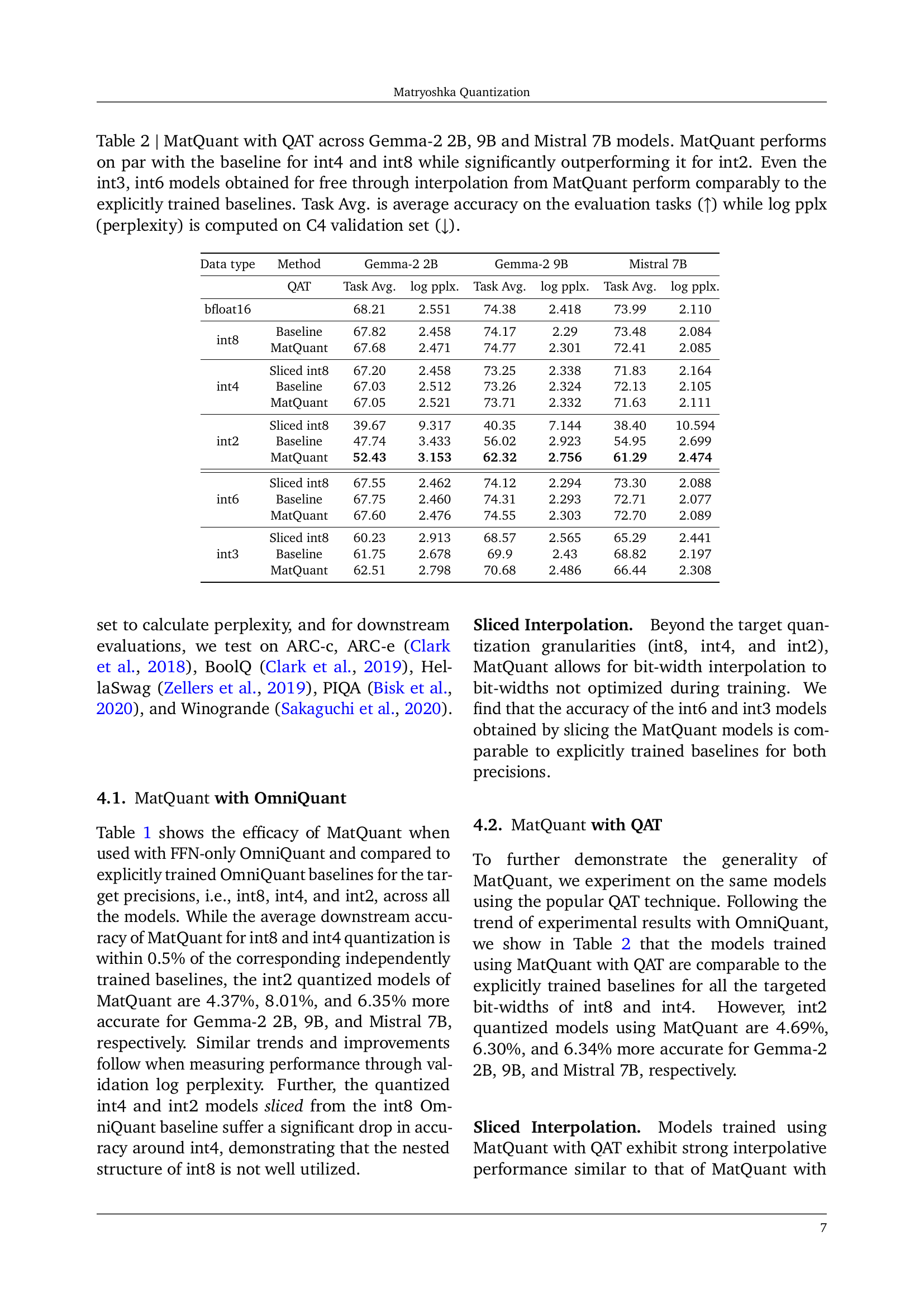
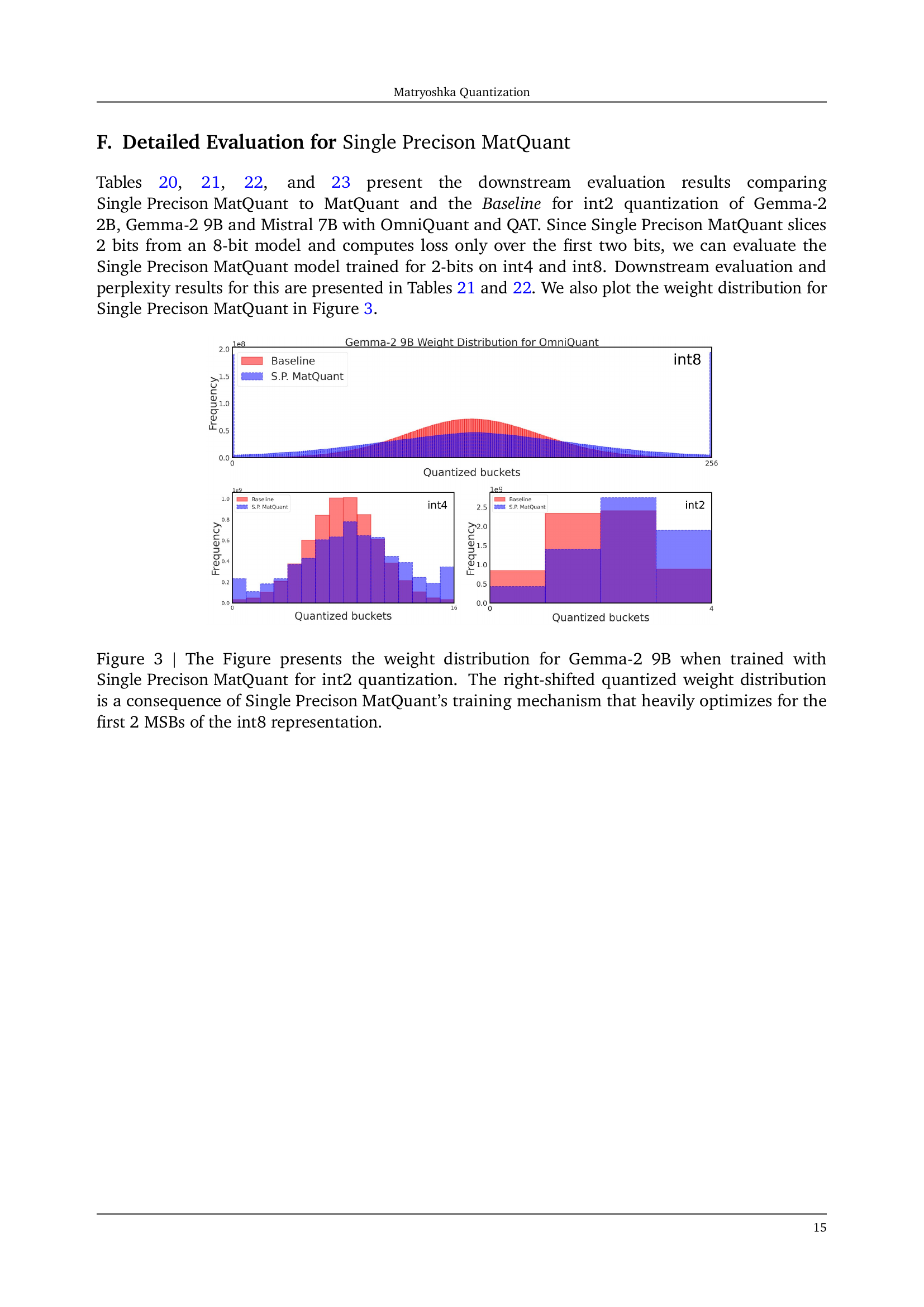
🔼 The figure shows the weight distribution for the Gemma-2 9B model when trained with Matryoshka Quantization (MatQuant) and OmniQuant. The x-axis represents the quantized buckets, and the y-axis represents the frequency. The figure highlights how MatQuant shifts the distribution of quantized weights toward higher values compared to the baseline. This shift is particularly noticeable for int2 models, where using more of the higher-valued weights leads to increased accuracy. This demonstrates that MatQuant allows for better utilization of the integer data type, particularly at low precisions.
read the caption
(c)
More on tables
| Data type | Method | Gemma-2 2B | Gemma-2 9B | Mistral 7B | |||
|---|---|---|---|---|---|---|---|
| QAT | Task Avg. | log pplx. | Task Avg. | log pplx. | Task Avg. | log pplx. | |
| bfloat16 | |||||||
| int8 | Baseline | ||||||
| int4 | Sliced int8 | ||||||
| Baseline | |||||||
| int2 | Sliced int8 | ||||||
| Baseline | |||||||
| int6 | Sliced int8 | ||||||
| Baseline | |||||||
| int3 | Sliced int8 | ||||||
| Baseline | |||||||
🔼 This table presents a comparison of the performance of Matryoshka Quantization (MatQuant) against baseline methods for quantizing the Gemma-2 2B, 9B, and Mistral 7B models using Quantization Aware Training (QAT). The comparison is made across different bit precisions (int8, int4, int2) and interpolated precisions (int6, int3). MatQuant’s performance is evaluated using average accuracy across downstream tasks and log perplexity on the C4 validation set. The results show that MatQuant achieves comparable or better accuracy than the baselines for various precision levels, demonstrating its effectiveness in multi-scale quantization.
read the caption
Table 2: MatQuantMatQuant{\rm MatQuant}roman_MatQuant with QAT across Gemma-2 2B, 9B and Mistral 7B models. MatQuantMatQuant{\rm MatQuant}roman_MatQuant performs on par with the baseline for int4 and int8 while significantly outperforming it for int2. Even the int3, int6 models obtained for free through interpolation from MatQuantMatQuant{\rm MatQuant}roman_MatQuant perform comparably to the explicitly trained baselines. Task Avg. is average accuracy on the evaluation tasks (↑↑\uparrow↑) while log pplx (perplexity) is computed on C4 validation set (↓↓\downarrow↓).
| Data type | Weightings | Gemma-2 2B | Gemma-2 9B | Mistral 7B |
|---|---|---|---|---|
| Task Avg. | ||||
| int8 | ||||
| int4 | ||||
| int2 | ||||
🔼 This table presents an ablation study on the effect of different loss weightings for the three target bit-widths (int8, int4, int2) during Matryoshka Quantization training. It shows how changing the relative importance of the loss functions for each bit-width impacts the final accuracy of the quantized models. The results are presented for the Gemma-2 2B, 9B, and Mistral 7B models. The baseline configuration uses equal weighting (1,1,1). The (0,0,1) configuration represents training only for int2 precision, and it is referred to as ‘Single Precision MatQuant’.
read the caption
Table 3: Design choice ablation for loss re-weighting of the 3 target bit-widths (int8, int4, int2) that MatQuantMatQuant{\rm MatQuant}roman_MatQuant explicitly optimizes. Note that MatQuantMatQuant{\rm MatQuant}roman_MatQuant (0,0,1)001(0,0,1)( 0 , 0 , 1 ) ≡\equiv≡ Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant.
| OmniQuant | QAT | ||||
|---|---|---|---|---|---|
| Data type | Config. | Task Avg. | log pplx. | Task Avg. | log pplx. |
| int8 | |||||
| int4 | |||||
| int2 | |||||
🔼 This table investigates the impact of co-distillation on Matryoshka Quantization (MatQuant). Co-distillation is a technique where the outputs of a higher-precision model are used as targets to train a lower-precision model. The experiment explores different configurations of distilling int2 and int4 models from an int8 model. The results demonstrate that co-distillation significantly improves the accuracy of the int2 model while having minimal effects on the int4 and int8 models. This highlights the effectiveness of leveraging the nested structure of MatQuant for multi-scale model training.
read the caption
Table 4: Design choice ablations for co-distillation within MatQuantMatQuant{\rm MatQuant}roman_MatQuant. x→y→xy\text{x}\rightarrow\text{y}x → y represents distilling the y-bit model from the x-bit model. We note that the accuracy for int2 has significantly improved while minimally impacting the other bit-widths.
| int2 | Gemma-2 2B | Gemma-2 9B | Mistral 7B | |||
|---|---|---|---|---|---|---|
| Method | Task Avg. | log pplx. | Task Avg. | log pplx. | Task Avg. | log pplx. |
| OmniQuant | ||||||
| S.P. | ||||||
| QAT | ||||||
| S.P. | ||||||
🔼 Table 5 presents a comparison of the performance of three different quantization methods for int2, int4, and int8 precision levels on the Gemma-2 9B model. The methods are: a baseline approach (where each precision level is trained independently); MatQuant (a multi-scale training technique); and Single Precision MatQuant (a variation of MatQuant that optimizes only for int2 precision). The table shows that Single Precision MatQuant significantly improves the accuracy of the int2 model compared to the baseline but, importantly, leads to substantially lower accuracy for int4 and int8. This suggests that there is a trade-off between optimizing for a single precision level versus multiple levels, and that this tradeoff is important to consider.
read the caption
Table 5: Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant significantly improves upon the baseline for int2 and, at times, outperforms MatQuantMatQuant{\rm MatQuant}roman_MatQuant. Crucially, int8 and int4 performances of Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant experience a significant accuracy decrease (Tables 21 & 22).
| Data type | Method | Gemma-2 9B | Mistral 7B | ||
|---|---|---|---|---|---|
| QAT | Task Avg. | log pplx. | Task Avg. | log pplx. | |
| bfloat16 | |||||
| int8 | Baseline | ||||
| int4 | Sliced int8 | ||||
| Baseline | |||||
| int2 | Sliced int8 | ||||
| Baseline | - | - | - | - | |
| S.P. | |||||
| int6 | Sliced int8 | ||||
| Baseline | |||||
| int3 | Sliced int8 | ||||
| Baseline | - | - | - | - | |
| S.P. | |||||
🔼 Table 6 presents the results of applying Matryoshka Quantization (MatQuant) and Single Precision MatQuant with Quantization Aware Training (QAT) to both Feed Forward Network (FFN) and Attention layers of transformer-based large language models (LLMs). The table compares the performance of different quantization levels (int8, int4, int2, int6, int3) across three model architectures (Gemma-2 2B, Gemma-2 9B and Mistral 7B). It highlights how MatQuant and Single Precision MatQuant stabilize performance at lower bit depths (int2 and int3) where standard QAT often struggles. This showcases the effectiveness of MatQuant in generating models that are both accurate and efficient.
read the caption
Table 6: Extending MatQuantMatQuant{\rm MatQuant}roman_MatQuant with QAT to FFN + Attention parameters. Baseline QAT destabilizes for int2 and int3 but improves significantly through MatQuantMatQuant{\rm MatQuant}roman_MatQuant & Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant.
| Data type | Method | Gemma-2 2B | ||||||
|---|---|---|---|---|---|---|---|---|
| OmniQuant | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | |
| bfloat16 | ||||||||
| int8 | Baseline | |||||||
| int4 | Sliced int8 | |||||||
| Baseline | ||||||||
| int2 | Sliced int8 | |||||||
| Baseline | ||||||||
| int6 | Sliced int8 | |||||||
| Baseline | ||||||||
| int3 | Sliced int8 | |||||||
| Baseline | ||||||||
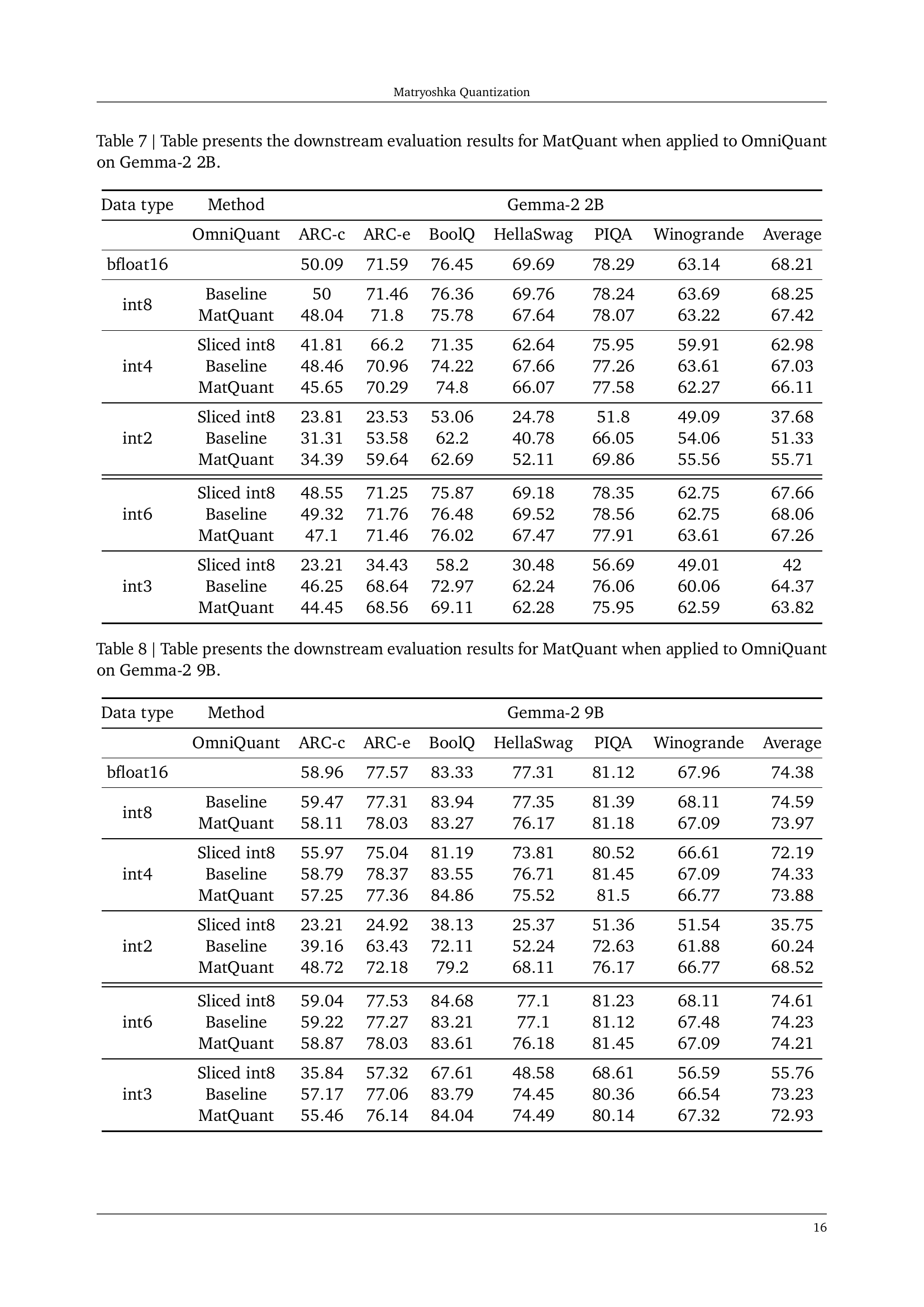
🔼 This table presents the downstream evaluation results of Matryoshka Quantization (MatQuant) when it is applied to the OmniQuant method on the Gemma-2 2B model. Downstream evaluation metrics such as accuracy across various tasks (ARC-c, ARC-e, BoolQ, HellaSwag, PIQA, and Winogrande) are shown for different quantization levels (int8, int4, int2, int6, int3). The results are compared against baseline OmniQuant and sliced int8 models for a comprehensive comparison. It highlights MatQuant’s performance across various bit precisions and its ability to generate multiple quantized models from a single trained model.
read the caption
Table 7: Table presents the downstream evaluation results for MatQuantMatQuant{\rm MatQuant}roman_MatQuant when applied to OmniQuant on Gemma-2 2B.
| Data type | Method | Gemma-2 9B | ||||||
|---|---|---|---|---|---|---|---|---|
| OmniQuant | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | |
| bfloat16 | ||||||||
| int8 | Baseline | |||||||
| int4 | Sliced int8 | |||||||
| Baseline | ||||||||
| int2 | Sliced int8 | |||||||
| Baseline | ||||||||
| int6 | Sliced int8 | |||||||
| Baseline | ||||||||
| int3 | Sliced int8 | |||||||
| Baseline | ||||||||
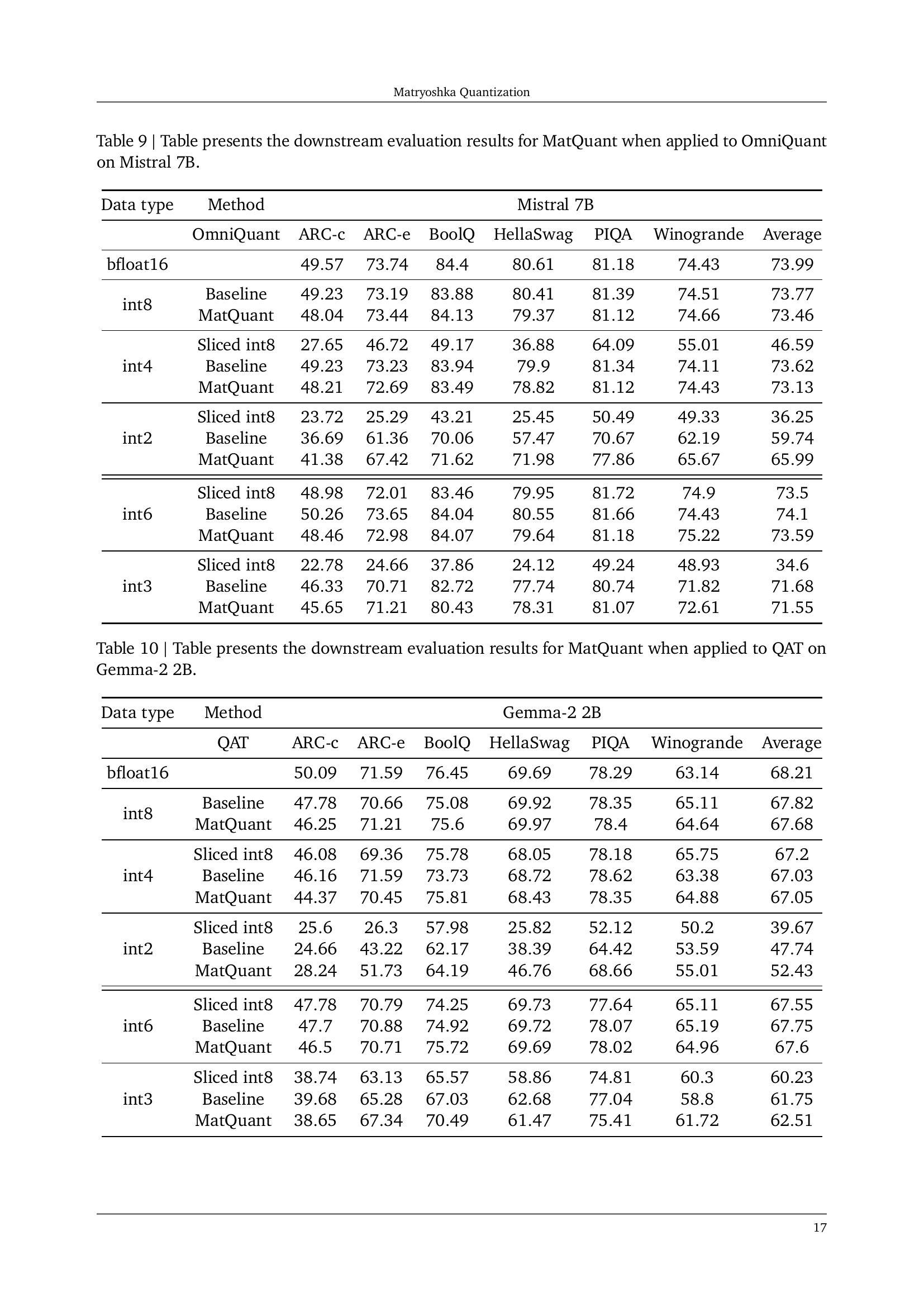
🔼 This table presents the downstream evaluation results for the Matryoshka Quantization (MatQuant) technique when used with OmniQuant on the Gemma-2 9B model. It shows the performance of MatQuant across different quantization levels (int8, int4, int2, int6, int3) on various downstream tasks such as ARC-c, ARC-e, BoolQ, HellaSwag, PIQA, and Winogrande. The results are compared against baselines representing standard OmniQuant without MatQuant and also those derived by slicing an int8 quantized model. This allows for a comparison of MatQuant’s multi-scale training approach against traditional single-precision quantization methods and to evaluate how it performs with interpolated bit-widths.
read the caption
Table 8: Table presents the downstream evaluation results for MatQuantMatQuant{\rm MatQuant}roman_MatQuant when applied to OmniQuant on Gemma-2 9B.
| Data type | Method | Mistral 7B | ||||||
|---|---|---|---|---|---|---|---|---|
| OmniQuant | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | |
| bfloat16 | ||||||||
| int8 | Baseline | |||||||
| int4 | Sliced int8 | |||||||
| Baseline | ||||||||
| int2 | Sliced int8 | |||||||
| Baseline | ||||||||
| int6 | Sliced int8 | |||||||
| Baseline | ||||||||
| int3 | Sliced int8 | |||||||
| Baseline | ||||||||
🔼 This table presents the downstream task evaluation results for the Matryoshka Quantization (MatQuant) method when used with OmniQuant on the Mistral 7B model. It shows the performance (accuracy and log-perplexity) for different quantization levels (int8, int4, int2, int6, int3). For each precision, MatQuant’s performance is compared against a baseline (explicitly trained for that precision) and the results from slicing a higher precision model (sliced int8). This allows for a comparison of the effectiveness of the multi-scale training method against training separate models at different precisions.
read the caption
Table 9: Table presents the downstream evaluation results for MatQuantMatQuant{\rm MatQuant}roman_MatQuant when applied to OmniQuant on Mistral 7B.
| Data type | Method | Gemma-2 2B | ||||||
|---|---|---|---|---|---|---|---|---|
| QAT | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | |
| bfloat16 | ||||||||
| int8 | Baseline | |||||||
| int4 | Sliced int8 | |||||||
| Baseline | ||||||||
| int2 | Sliced int8 | |||||||
| Baseline | ||||||||
| int6 | Sliced int8 | |||||||
| Baseline | ||||||||
| int3 | Sliced int8 | |||||||
| Baseline | ||||||||
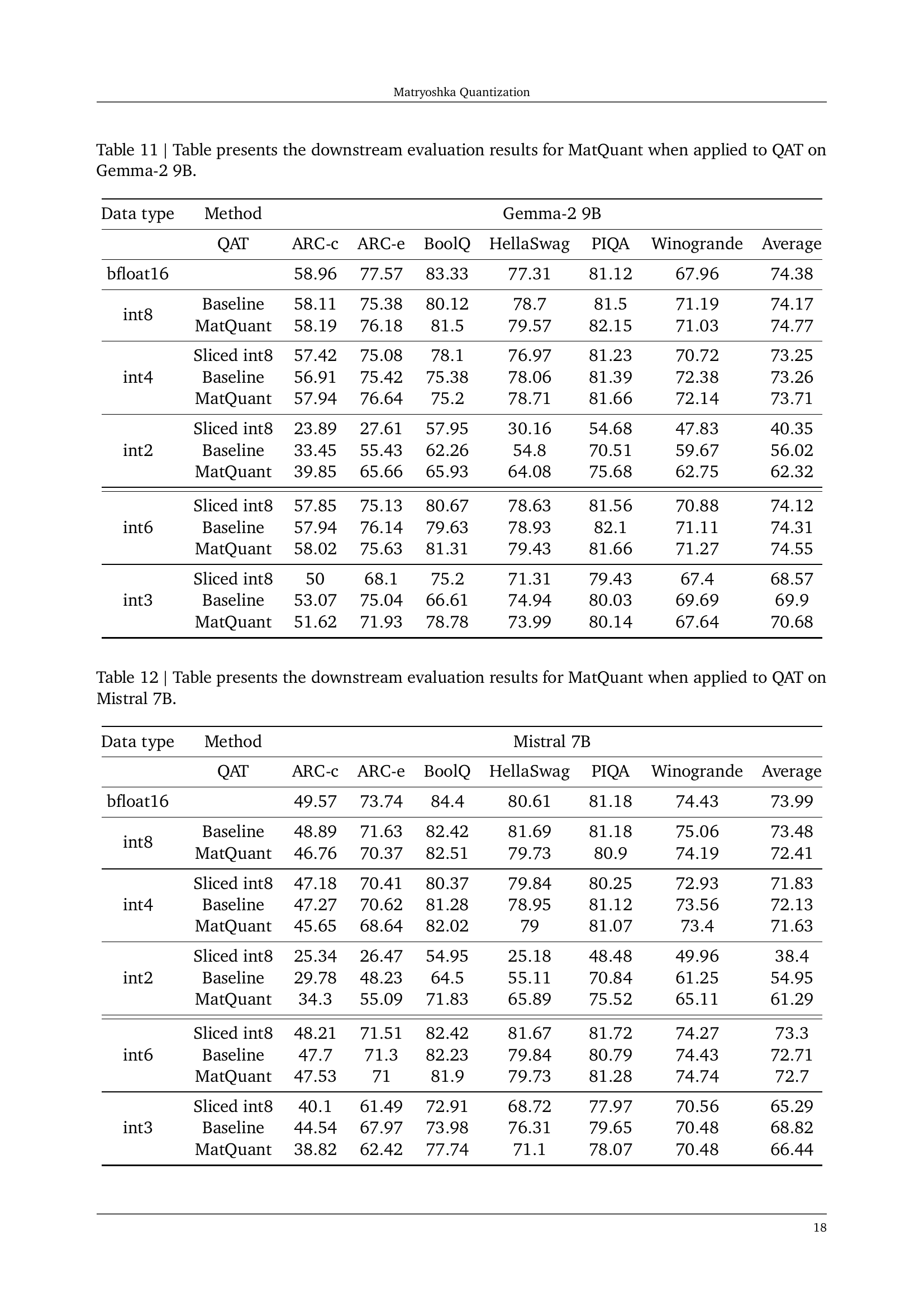
🔼 This table presents the downstream evaluation results for the Matryoshka Quantization (MatQuant) method when applied to Quantization Aware Training (QAT) on the Gemma-2 2B model. It compares the performance of MatQuant across different bit-widths (int8, int4, int2, int6, and int3) against baseline models trained with QAT at each bit-width. The evaluation metrics include accuracy on various downstream tasks (ARC-c, ARC-e, BoolQ, HellaSwag, PIQA, and Winogrande) and average perplexity on the C4 validation set. It also includes results for models derived from MatQuant via interpolation (sliced int8) to show the adaptability and efficiency of MatQuant in generating models that perform well at different bit-widths without retraining.
read the caption
Table 10: Table presents the downstream evaluation results for MatQuantMatQuant{\rm MatQuant}roman_MatQuant when applied to QAT on Gemma-2 2B.
| Data type | Method | Gemma-2 9B | ||||||
|---|---|---|---|---|---|---|---|---|
| QAT | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | |
| bfloat16 | ||||||||
| int8 | Baseline | |||||||
| int4 | Sliced int8 | |||||||
| Baseline | ||||||||
| int2 | Sliced int8 | |||||||
| Baseline | ||||||||
| int6 | Sliced int8 | |||||||
| Baseline | ||||||||
| int3 | Sliced int8 | |||||||
| Baseline | ||||||||
🔼 This table displays the performance of Matryoshka Quantization (MatQuant) when integrated with Quantization Aware Training (QAT) on the Gemma-2 9B model. It compares the average accuracy across several downstream tasks for various quantization bit-widths (int8, int4, int2, int6, int3). The table includes results for MatQuant, baselines (explicitly trained models for each precision), and models obtained by slicing an int8-quantized model. This allows for a comparison of MatQuant’s multi-scale training approach against independently trained models of different precisions, highlighting MatQuant’s ability to efficiently create multiple models from a single trained model.
read the caption
Table 11: Table presents the downstream evaluation results for MatQuantMatQuant{\rm MatQuant}roman_MatQuant when applied to QAT on Gemma-2 9B.
| Data type | Method | Mistral 7B | ||||||
|---|---|---|---|---|---|---|---|---|
| QAT | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | |
| bfloat16 | ||||||||
| int8 | Baseline | |||||||
| int4 | Sliced int8 | |||||||
| Baseline | ||||||||
| int2 | Sliced int8 | |||||||
| Baseline | ||||||||
| int6 | Sliced int8 | |||||||
| Baseline | ||||||||
| int3 | Sliced int8 | |||||||
| Baseline | ||||||||
🔼 This table presents the downstream evaluation results for the Matryoshka Quantization (MatQuant) technique when applied to Quantization Aware Training (QAT) using the Mistral 7B model. It shows the performance of MatQuant across multiple bit-widths (int8, int4, int2, int6, int3) on various downstream tasks, comparing its results to both a standard baseline and a baseline where lower-precision models are created by simply slicing the bits from an int8-quantized model. The metrics used include average accuracy across the downstream tasks and log perplexity.
read the caption
Table 12: Table presents the downstream evaluation results for MatQuantMatQuant{\rm MatQuant}roman_MatQuant when applied to QAT on Mistral 7B.
| Gemma-2 2B | ||||||||
|---|---|---|---|---|---|---|---|---|
| Data type | Weightings | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average |
| int8 | ||||||||
| int4 | ||||||||
| int2 | ||||||||
| int6 | ||||||||
| int3 | ||||||||
🔼 This table presents the downstream evaluation results for the Gemma-2 2B model when using Matryoshka Quantization (MatQuant) with OmniQuant. It shows the impact of different loss weightings applied during MatQuant training on the accuracy of the quantized model across various bit-widths (int8, int4, int2, int6, int3). The loss weightings represent the relative importance given to the different bit-widths in the optimization process, allowing the exploration of different trade-offs between the accuracy levels across precisions. The results are shown for different weight combinations, allowing comparison of performance based on these weighting schemes.
read the caption
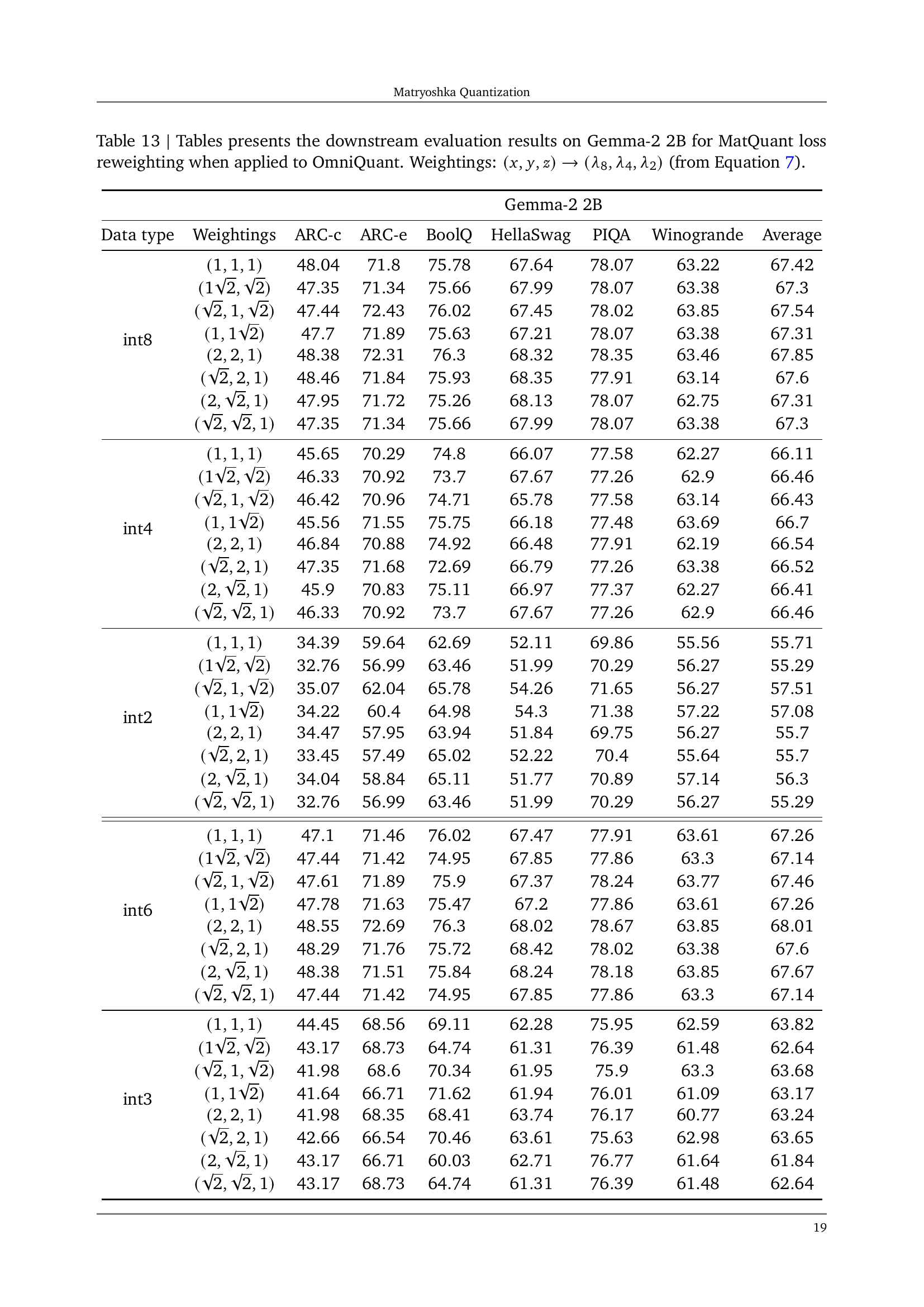
Table 13: Tables presents the downstream evaluation results on Gemma-2 2B for MatQuantMatQuant{\rm MatQuant}roman_MatQuant loss reweighting when applied to OmniQuant. Weightings: (x,y,z)→(λ8,λ4,λ2)→𝑥𝑦𝑧subscript𝜆8subscript𝜆4subscript𝜆2(x,y,z)\rightarrow(\lambda_{8},\lambda_{4},\lambda_{2})( italic_x , italic_y , italic_z ) → ( italic_λ start_POSTSUBSCRIPT 8 end_POSTSUBSCRIPT , italic_λ start_POSTSUBSCRIPT 4 end_POSTSUBSCRIPT , italic_λ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) (from Equation 7).
| Gemma-2 9B | ||||||||
|---|---|---|---|---|---|---|---|---|
| Data type | Weightings | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average |
| int8 | ||||||||
| int4 | ||||||||
| int2 | ||||||||
| int6 | ||||||||
| int3 | ||||||||
🔼 This table presents the downstream evaluation results of the Matryoshka Quantization (MatQuant) method on the Gemma-2 9B model when using OmniQuant. The experiment focuses on the impact of different weightings applied during training. The weightings control the relative importance of achieving high accuracy at different bit precisions (int8, int4, int2), which are determined by the λ parameters in Equation 7 of the paper. Each row represents a different set of weightings, showing how the average accuracy across multiple downstream tasks changes. The table allows comparison of MatQuant’s performance under various weighting schemes to a baseline (no weighting) and to versions where precision levels are derived by simply slicing from the int8 weights.
read the caption
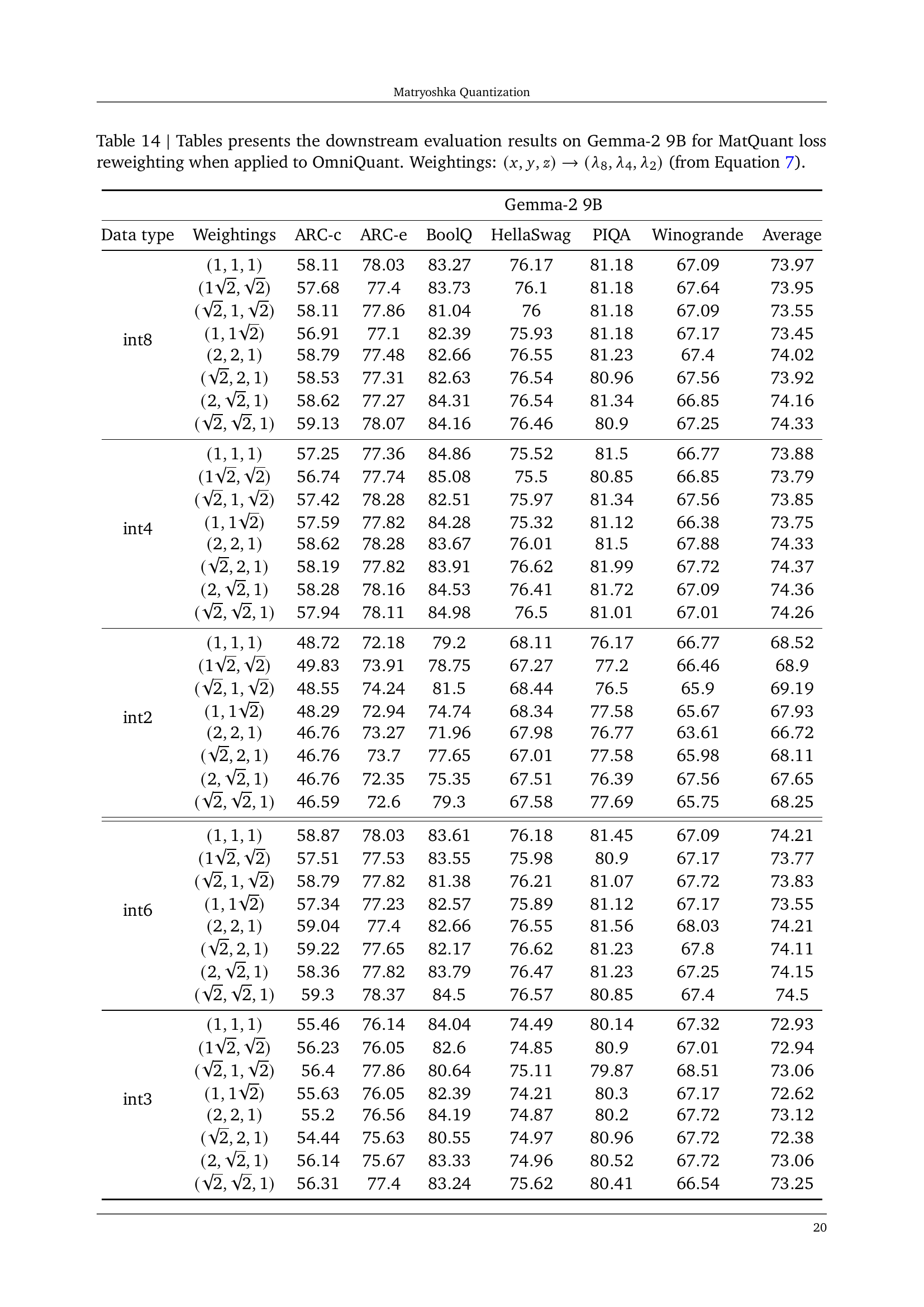
Table 14: Tables presents the downstream evaluation results on Gemma-2 9B for MatQuantMatQuant{\rm MatQuant}roman_MatQuant loss reweighting when applied to OmniQuant. Weightings: (x,y,z)→(λ8,λ4,λ2)→𝑥𝑦𝑧subscript𝜆8subscript𝜆4subscript𝜆2(x,y,z)\rightarrow(\lambda_{8},\lambda_{4},\lambda_{2})( italic_x , italic_y , italic_z ) → ( italic_λ start_POSTSUBSCRIPT 8 end_POSTSUBSCRIPT , italic_λ start_POSTSUBSCRIPT 4 end_POSTSUBSCRIPT , italic_λ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) (from Equation 7).
| Mistral 7B | ||||||||
|---|---|---|---|---|---|---|---|---|
| Data type | Weightings | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average |
| int8 | ||||||||
| int4 | ||||||||
| int2 | ||||||||
| int6 | ||||||||
| int3 | ||||||||
🔼 This table presents the results of a downstream evaluation on the Mistral 7B model. The experiment involves Matryoshka Quantization (MatQuant) with OmniQuant, focusing on the effect of different loss weightings during training. The loss weights (λ8, λ4, λ2) control the relative importance of the int8, int4, and int2 precision levels during optimization. The table shows the performance metrics (accuracy across various downstream tasks) for different precision levels (int8, int4, int2, int6, int3) resulting from varying these loss weights, providing insights into the trade-offs involved in multi-scale quantization.
read the caption
Table 15: Tables presents the downstream evaluation results on Mistral 7B for MatQuantMatQuant{\rm MatQuant}roman_MatQuant loss reweighting when applied to OmniQuant. Weightings: (x,y,z)→(λ8,λ4,λ2)→𝑥𝑦𝑧subscript𝜆8subscript𝜆4subscript𝜆2(x,y,z)\rightarrow(\lambda_{8},\lambda_{4},\lambda_{2})( italic_x , italic_y , italic_z ) → ( italic_λ start_POSTSUBSCRIPT 8 end_POSTSUBSCRIPT , italic_λ start_POSTSUBSCRIPT 4 end_POSTSUBSCRIPT , italic_λ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) (from Equation 7).
| OmniQuant | Gemma-2 9B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Data type | Config. | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | log pplx. |
| int8 | |||||||||
| int4 | |||||||||
| int2 | |||||||||
| int6 | |||||||||
| int3 | |||||||||
🔼 This table displays the results of downstream evaluations and perplexity calculations for the Matryoshka Quantization (MatQuant) model using OmniQuant on the Gemma-2 9B model. It shows the impact of co-distillation on the model’s performance across different precision levels (int8, int4, int2, int6, int3). The table presents the average accuracy across various downstream tasks and the log perplexity scores on a validation set. Different co-distillation configurations are compared to assess their effects on downstream performance and model complexity. Each row corresponds to a specific set of hyperparameters used during the training process.
read the caption
Table 16: Table presents the downstream evaluation and perplexity results for our MatQuantMatQuant{\rm MatQuant}roman_MatQuant co-distillation experiments on Gemma-2 9B with OmniQuant.
| QAT | Gemma-2 9B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Data type | Config. | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | log pplx. |
| int8 | |||||||||
| int4 | |||||||||
| int2 | |||||||||
| int6 | |||||||||
| int3 | |||||||||
🔼 Table 17 presents the downstream evaluation and perplexity results for the Matryoshka Quantization (MatQuant) co-distillation experiments on the 9B parameter Gemma-2 model using Quantization Aware Training (QAT). It shows the performance across various downstream tasks (ARC-c, ARC-e, BoolQ, HellaSwag, PIQA, Winogrande) and the associated perplexity scores on a validation set. Different configurations of MatQuant co-distillation are compared, varying the precision levels (int8, int4, int2, int6, int3) and whether or not co-distillation is applied. The table allows readers to compare the effects of different co-distillation strategies on downstream task performance and perplexity.
read the caption
Table 17: Table presents the downstream evaluation and perplexity results for our MatQuantMatQuant{\rm MatQuant}roman_MatQuant co-distillation experiments on Gemma-2 9B with QAT.
| Data type | Method | Gemma-2 9B | ||||||
| ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | ||
| bfloat16 | ||||||||
| int8 | Baseline | |||||||
| int4 | Sliced int8 | |||||||
| Baseline | ||||||||
| int2 | Sliced int8 | |||||||
| Baseline | - | - | - | - | - | - | - | |
| S.P. | ||||||||
| int6 | Sliced int8 | |||||||
| Baseline | ||||||||
| int3 | Sliced int8 | |||||||
| Baseline | - | - | - | - | - | - | - | |
| S.P. | ||||||||
🔼 This table presents the results of a downstream evaluation on the Gemma-2 9B model. The evaluation assesses the performance of Matryoshka Quantization (MatQuant) when applied to Feed-Forward Network (FFN) and Attention layers using Quantization Aware Training (QAT). The table compares MatQuant’s performance across different quantization levels (int8, int4, int2, int6, and int3), showing accuracy and perplexity scores. It also includes results for baselines (models trained without MatQuant) and sliced models (models created by directly truncating higher precision weights). The purpose of the table is to demonstrate the effectiveness and flexibility of MatQuant in achieving high accuracy at various bit-widths, especially lower precisions like int2.
read the caption
Table 18: Table presents the downstream evaluation results for MatQuantMatQuant{\rm MatQuant}roman_MatQuant FFN + Attention quantization on Gemma-2 9B with QAT.
| Data type | Method | Mistral 7B | ||||||
| ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | ||
| bfloat16 | ||||||||
| int8 | Baseline | |||||||
| int4 | Sliced int8 | |||||||
| Baseline | ||||||||
| int2 | Sliced int8 | |||||||
| Baseline | - | - | - | - | - | - | - | |
| S.P. | ||||||||
| int6 | Sliced int8 | |||||||
| Baseline | ||||||||
| int3 | Sliced int8 | |||||||
| Baseline | - | - | - | - | - | - | - | |
| S.P. | ||||||||
🔼 Table 19 presents the downstream evaluation results for the Matryoshka Quantization (MatQuant) technique applied to the Feed-Forward Network (FFN) and Attention layers of the Mistral 7B model using Quantization Aware Training (QAT). It shows the performance (accuracy on downstream tasks and log perplexity on a validation set) of different quantization levels (int8, int4, int2, int6, int3) achieved using MatQuant, as compared to baselines where models are trained separately for each level. It also includes results for models obtained via interpolation from an int8 model using MatQuant’s multi-scale capability. This table illustrates MatQuant’s effectiveness in training a single model capable of performing well at various precision levels, and its ability to generate high-quality interpolated models.
read the caption
Table 19: Table presents the downstream evaluation results for MatQuantMatQuant{\rm MatQuant}roman_MatQuant FFN + Attention quantization on Mistral 7B with QAT.
| int2 | Gemma2-2B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Task Avg. | pplx. | |
| OmniQuant | S.P. | ||||||||
| Baseline | |||||||||
| QAT | S.P. | ||||||||
| Baseline | |||||||||
🔼 Table 20 presents a comparison of the performance of three different quantization methods: Single Precision MatQuant, MatQuant, and a baseline method. All three methods are applied to a Gemma-2 2B model, using both OmniQuant and QAT (two different quantization training approaches). The table shows downstream evaluation metrics (accuracy on various tasks) and perplexity scores for int2 quantization, highlighting the trade-offs in accuracy and computational cost among the different techniques.
read the caption
Table 20: Table presents downstream evaluation and perplexity results for Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant, comparing it with MatQuantMatQuant{\rm MatQuant}roman_MatQuant and the Baseline for int2 quatization of Gemma-2 2B with OmniQuant and QAT.
| Gemma-2 9B | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Data type | Method | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | pplx. |
| int8 | S.P. | ||||||||
| OmniQuant | |||||||||
| MatQuant | |||||||||
| int4 | S.P. | ||||||||
| OmniQuant | |||||||||
| MatQuant | |||||||||
| int2 | S.P. | ||||||||
| OmniQuant | |||||||||
| MatQuant | |||||||||
🔼 This table presents a comparison of downstream evaluation and perplexity results for three different quantization methods applied to the Gemma-2 9B model: Single Precision MatQuant, MatQuant, and a baseline. Single Precision MatQuant is a variation where the model is specifically trained only for 2-bit precision (int2), and the int4 and int8 models are derived by slicing the weights from this trained model. MatQuant, in contrast, jointly optimizes for multiple bit-widths (int2, int4, int8). The baseline represents models trained independently for each bit-width. The comparison allows assessing the performance of Single Precision MatQuant relative to MatQuant and the standard method of independent training for each precision. The results are provided for OmniQuant.
read the caption
Table 21: Table presents downstream evaluation and perplexity results for Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant, comparing it with MatQuantMatQuant{\rm MatQuant}roman_MatQuant and the Baseline for int2, int4, int8 quatization of Gemma-2 9B with OmniQuant. Note that the model was trained with Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant for int2, the int4 and int8 model were sliced post training.
| Gemma-2 9B | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Data type | Method | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Average | log pplx. |
| int8 | S.P. | ||||||||
| QAT | |||||||||
| MatQuant | |||||||||
| int4 | S.P. | ||||||||
| QAT | |||||||||
| MatQuant | |||||||||
| int2 | S.P. | ||||||||
| QAT | |||||||||
| MatQuant | |||||||||
🔼 Table 22 presents a comparison of downstream evaluation and perplexity results for three different quantization methods applied to the Gemma-2 9B model using QAT. The methods compared are: the baseline (explicitly trained models for each precision), MatQuant (a multi-scale quantization method), and Single Precision MatQuant (a variation of MatQuant focusing solely on int2 precision). Crucially, Single Precision MatQuant only trained for int2 precision, while the int4 and int8 models were derived by slicing the trained weights, highlighting its ability to generate multiple precision models from a single training process. The table details the performance of each method across different precision levels (int2, int4, int8), showing accuracy and perplexity scores for each.
read the caption
Table 22: Table presents downstream evaluation and perplexity results for Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant, comparing it with MatQuantMatQuant{\rm MatQuant}roman_MatQuant and the Baseline for int2, int4, int8 quatization of Gemma-2 9B with QAT. Note that the model was trained with Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant for int2, the int4 and int8 model were sliced post training.
| int2 | Mistral 7B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | ARC-c | ARC-e | BoolQ | HellaSwag | PIQA | Winogrande | Task Avg. | pplx. | |
| OmniQuant | S.P. | ||||||||
| Baseline | |||||||||
| QAT | S.P. | ||||||||
| Baseline | |||||||||
🔼 Table 23 presents a comparison of the downstream evaluation and perplexity results for three different methods of quantizing the Mistral 7B model to 2 bits: Single Precision MatQuant, MatQuant, and a baseline method. Both OmniQuant and QAT training methods are included in the comparison. The table shows the results across several evaluation metrics, providing a comprehensive analysis of each method’s performance.
read the caption
Table 23: Table presents downstream evaluation and perplexity results for Single Precison MatQuantSingle Precison MatQuant{\rm Single\text{ }Precison\text{ }MatQuant}roman_Single roman_Precison roman_MatQuant, comparing it with MatQuantMatQuant{\rm MatQuant}roman_MatQuant and the Baseline for int2 quatization of Mistral 7B with OmniQuant and QAT.
Full paper#