TL;DR#
Current large language models (LLMs) struggle with complex reasoning tasks. Existing methods for improving their reasoning capabilities are either proprietary or computationally expensive. This creates a need for more efficient and easily replicable techniques.
This paper introduces a data-efficient and parameter-efficient approach to train LLMs for complex reasoning. The researchers found that by fine-tuning a model on a relatively small number of demonstrations, they could significantly improve its reasoning abilities. Crucially, they discovered that the structure of the reasoning steps in the demonstrations is far more important than the correctness of the individual steps or the specific content. This insight has significant implications for the design and training of future LLMs focused on reasoning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language models (LLMs) and reasoning. It demonstrates a surprisingly data-efficient and parameter-efficient method for teaching LLMs to reason using chain-of-thought prompting. The findings challenge existing assumptions and open new avenues for research on LLM reasoning capabilities and training techniques. This work is highly relevant to current trends in efficient LLM training and improving reasoning abilities.
Visual Insights#

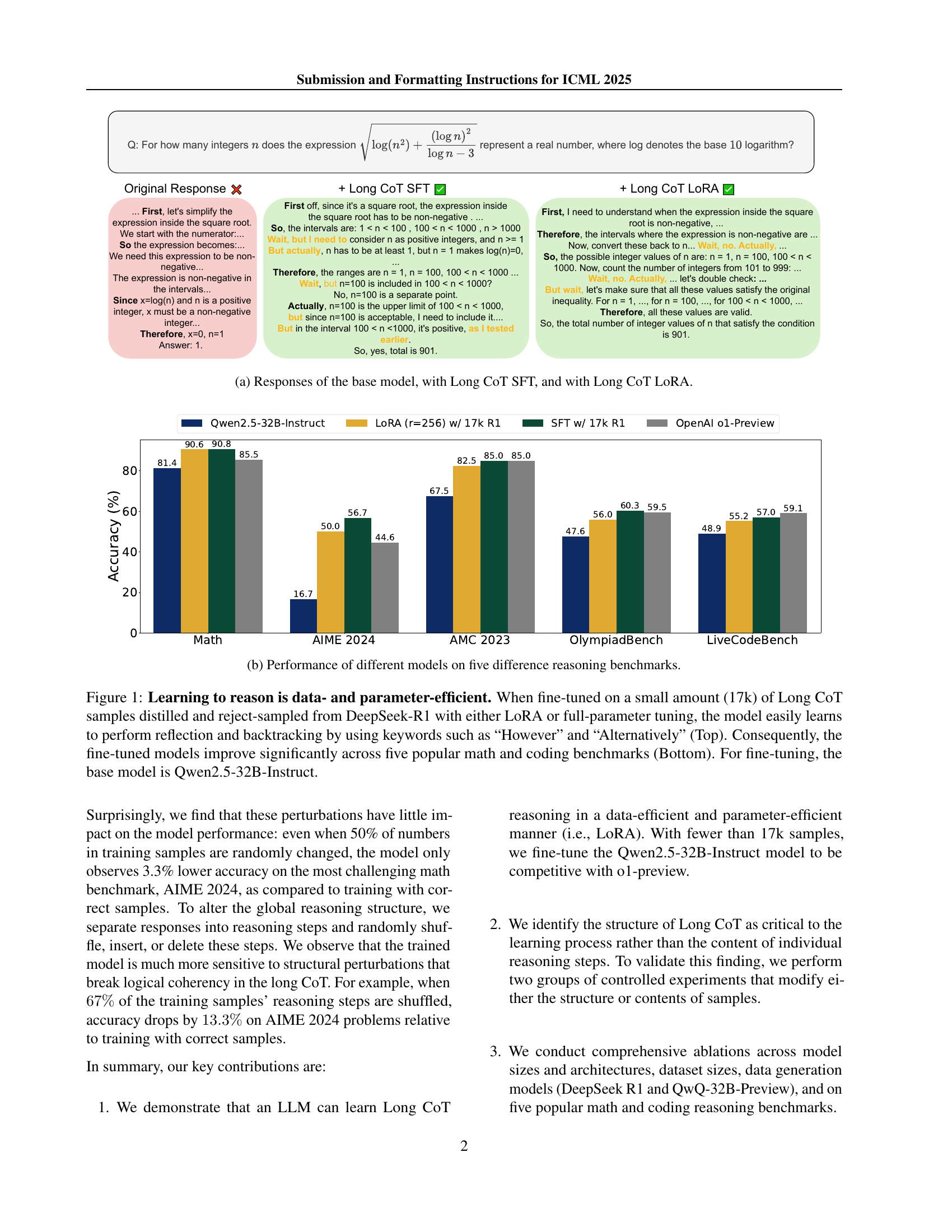
🔼 This figure shows the comparison of three different models’ responses to the same question. The first is the base model, which does not utilize Long Chain of Thought (Long CoT) reasoning. The second model uses Long CoT reasoning trained via supervised fine-tuning (SFT), and the third model uses Long CoT reasoning fine-tuned with low-rank adaptation (LoRA). The different response styles and quality highlight the impact of Long CoT training on the model’s reasoning ability.
read the caption
(a) Responses of the base model, with Long CoT SFT, and with Long CoT LoRA.
| MATH500 | AIME24 | AMC23 | Olympiad. | LCB. | |
| Qwen2.5-32B-Inst. | 84.8 | 16.7 | 67.5 | 47.6 | 48.9 |
| QwQ | 90.4 | 33.3 | 75.0 | 58.1 | 59.1 |
| o1-preview | 85.5 | 44.6 | 87.5 | 59.2 | 59.1 |
| 7k QwQ Samples | |||||
| SFT | 87.8 | 33.3 | 77.5 | 57.3 | 57.5 |
| LoRA (r=64) | 86.6 | 40.0 | 77.5 | 57.2 | 56.6 |
| 17k QwQ Samples | |||||
| SFT | 87.8 | 33.3 | 70.0 | 56.7 | 57.9 |
| LoRA (r=64) | 86.6 | 33.3 | 90.0 | 56.0 | 56.2 |
🔼 This table presents the performance of fine-tuning the Qwen2.5-32B-Instruct model using both full parameter fine-tuning (SFT) and low-rank adaptation (LoRA) on the task of generating Long Chain-of-Thought (Long CoT) reasoning. The model was trained with 7k and 17k samples from the QwQ dataset. The results are shown across five different reasoning benchmarks: Math-500, AIME 2024, AMC 23, OlympiadBench, and LiveCodeBench. The table highlights the parameter efficiency of learning Long CoT reasoning, demonstrating competitive performance with the proprietary 01-preview model using significantly fewer parameters and a smaller dataset.
read the caption
Table 1: Model accuracy with SFT and LoRA (rank=64). Fine-tuning performed on Qwen2.5-32B-Instruct with QwQ samples. “Olympiad.” is short for “OlympiadBench”, “LCB.” is short for “LiveCodeBench”. We find that the learning process of Long CoT can be parameter efficient.
In-depth insights#
LLM Reasoning Distillation#
LLM Reasoning Distillation explores the efficient transfer of reasoning capabilities from a large language model (LLM) to another, often a smaller or more resource-constrained model. This process leverages the knowledge embedded within a powerful, pre-trained LLM, acting as a teacher, to improve the reasoning skills of a student LLM. Data efficiency is a core principle; rather than training from scratch, the student LLM is fine-tuned using a relatively small, curated dataset of reasoning examples generated by the teacher. Parameter efficiency is another key aspect, often utilizing techniques like LoRA (Low-Rank Adaptation) to minimize the number of updated parameters in the student model, reducing computational costs. Furthermore, the research emphasizes the significance of the structural elements of the reasoning process over the precise content of individual steps. The structure, reflecting the logical flow, reflection, and revision, proves critical for successful knowledge transfer. This distillation approach thus highlights a path towards more affordable and accessible LLM-based reasoning systems.
Long CoT Structure#
The research emphasizes the crucial role of Long Chain of Thought (Long CoT) structure in effective reasoning, surpassing the significance of individual step content. Experiments involving content perturbations (incorrect answers, altered digits, keyword removal) resulted in minimal performance drops, highlighting the model’s robustness to factual errors. Conversely, structural modifications (shuffling, deleting, inserting steps) significantly impaired accuracy, demonstrating that logical flow and coherence are paramount for successful reasoning. This underscores that LLMs don’t just need correct information, but rather a well-organized, structured reasoning process to excel. The findings suggest that future LLM training should prioritize the development of robust, logically consistent reasoning structures over merely accumulating factual knowledge. Data efficiency is also highlighted, showing that a small number of well-structured Long CoT samples are sufficient to train effective reasoning models, advocating for a shift towards structured data curation in LLM development.
Data-Efficient Tuning#
Data-efficient tuning in large language models (LLMs) focuses on achieving significant performance improvements with minimal training data. This is crucial for reducing computational costs and time associated with training, making LLMs more accessible and sustainable. Effective techniques often involve leveraging existing models or carefully curated datasets. The core idea is to transfer knowledge from a larger, well-trained model (the teacher) to a smaller, less-trained model (the student) using a relatively small number of high-quality examples. This approach contrasts with traditional methods that require vast amounts of data for optimal performance. By meticulously selecting and utilizing representative training data, data-efficient tuning significantly lowers the resource demands of LLM training while retaining or even surpassing the performance of models trained with much larger datasets. The key is not simply reducing the quantity of data but also improving its quality and relevance, ensuring the small dataset accurately reflects the nuances of the target task.
Structural Sensitivity#
The concept of ‘Structural Sensitivity’ in the context of large language models (LLMs) and their reasoning capabilities highlights the crucial role of the logical organization of the reasoning process, rather than the specific content of individual steps. The research emphasizes that while minor alterations to the content (e.g., incorrect numbers or missing keywords) have minimal impact on performance, disruptions to the structural integrity of the reasoning chain, such as shuffling or deleting steps, significantly impair the model’s ability to generate correct and coherent responses. This finding underscores the importance of designing training data that prioritizes structural consistency and logical flow. The effectiveness of LLM reasoning is not solely dependent on factual knowledge but heavily influenced by the architecture and sequencing of the reasoning steps. Data efficiency can be substantially improved by focusing on structural correctness, thus making the training process for sophisticated reasoning tasks more efficient and less resource-intensive. Future research in this area should concentrate on developing strategies to create and optimize the structure of training data for improved LLM reasoning performance.
Future Directions#
Future research could explore scaling Long CoT learning to even larger language models, investigating potential limitations and exploring techniques to maintain efficiency. Understanding the interplay between model architecture and Long CoT effectiveness is crucial, potentially revealing architectural modifications to enhance learning. The impact of different training data generation methods on the quality and efficiency of Long CoT learning also deserves further scrutiny. A deeper exploration of the relationship between prompt engineering and the elicitation of effective Long CoT reasoning is needed, as is further investigation into robustness against adversarial attacks or noisy data. Finally, exploring applications of Long CoT reasoning in more diverse domains such as scientific discovery, complex problem-solving in robotics, and creative content generation would demonstrate the true potential of this learning paradigm.
More visual insights#
More on figures

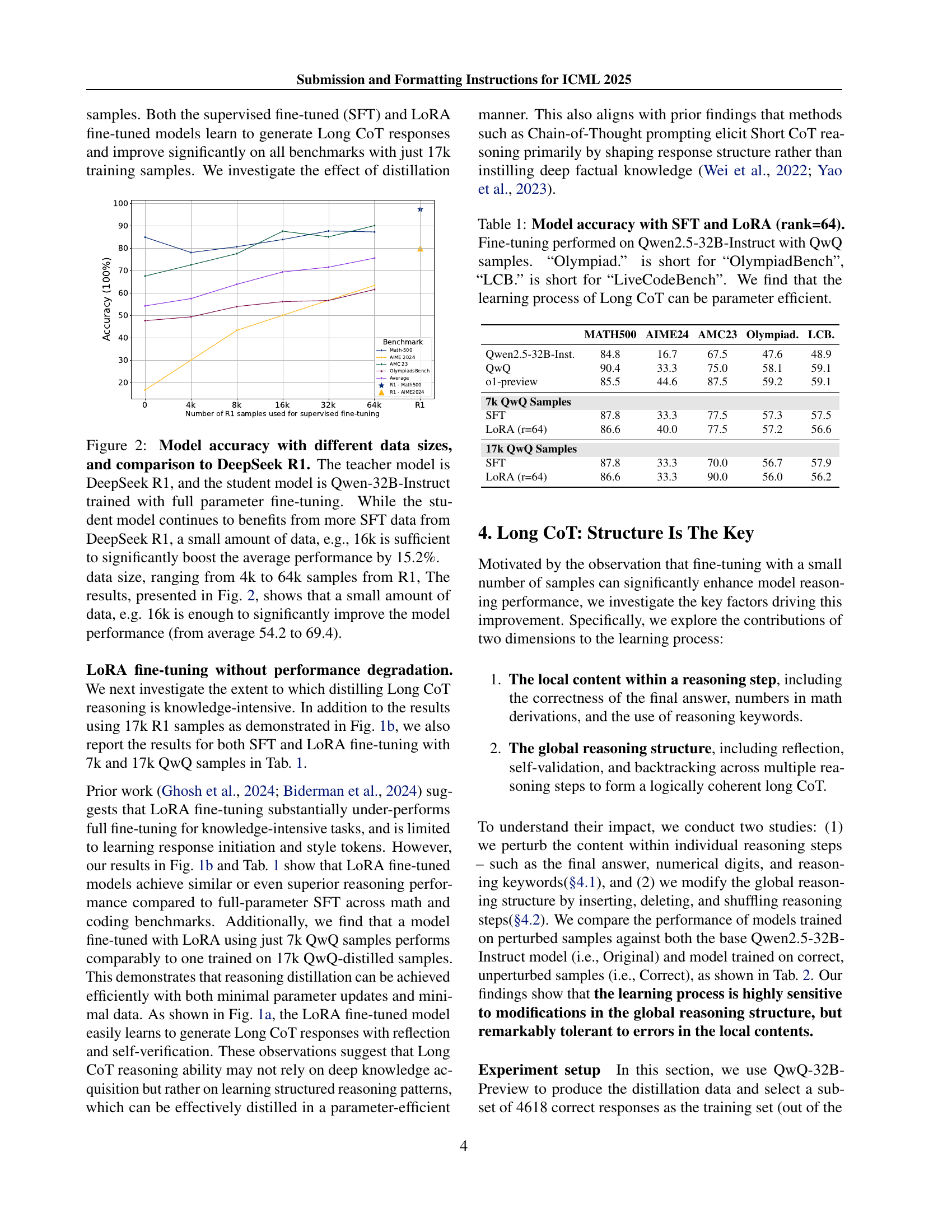
🔼 The bar chart compares the performance of different LLMs (Large Language Models) on five reasoning benchmarks: Math-500, AIME 2024, AMC 2023, OlympiadBench, and LiveCodeBench. It shows the accuracy achieved by different models, including Qwen2.5-32B-Instruct with and without fine-tuning using Long Chain of Thought (Long CoT) samples, and also includes the performance of the OpenAI o1-preview model as a reference point. This visual representation allows for easy comparison of the different models across various reasoning tasks, highlighting the impact of Long CoT fine-tuning on model performance.
read the caption
(b) Performance of different models on five difference reasoning benchmarks.

🔼 This figure demonstrates the data and parameter efficiency of fine-tuning a large language model (LLM) to perform Long Chain-of-Thought (Long CoT) reasoning. The top panel shows example Long CoT reasoning outputs, highlighting the use of keywords like ‘However’ and ‘Alternatively’ which indicate reflection and backtracking. The bottom panel displays a significant performance improvement across five popular math and coding benchmarks after fine-tuning with only 17,000 Long CoT samples using either Low-Rank Adaptation (LoRA) or full parameter-tuning. The base model used for fine-tuning was Qwen2.5-32B-Instruct.
read the caption
Figure 1: Learning to reason is data- and parameter-efficient. When fine-tuned on a small amount (17k) of Long CoT samples distilled and reject-sampled from DeepSeek-R1 with either LoRA or full-parameter tuning, the model easily learns to perform reflection and backtracking by using keywords such as “However” and “Alternatively” (Top). Consequently, the fine-tuned models improve significantly across five popular math and coding benchmarks (Bottom). For fine-tuning, the base model is Qwen2.5-32B-Instruct.

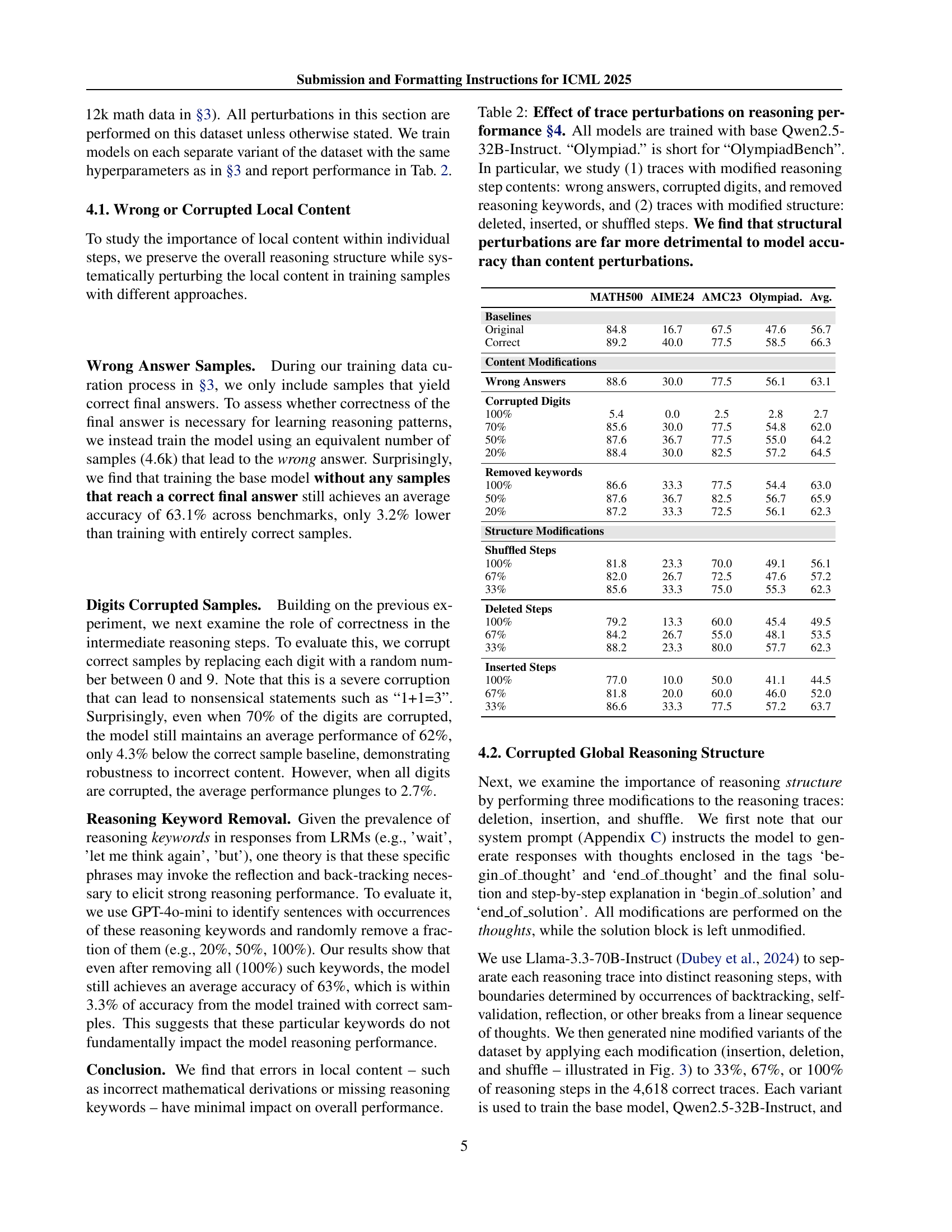
🔼 This figure shows the impact of different training data sizes on the accuracy of a Qwen-32B-Instruct language model fine-tuned using the DeepSeek R1 model as a teacher. The x-axis represents the number of training samples from the DeepSeek R1 model, and the y-axis shows the average accuracy across five reasoning benchmarks. The figure demonstrates that even a relatively small amount of training data (e.g., 16,000 samples) leads to a significant improvement in the student model’s performance, achieving a 15.2% increase in average accuracy. The plot also includes the performance of the DeepSeek R1 model for comparison.
read the caption
Figure 2: Model accuracy with different data sizes, and comparison to DeepSeek R1. The teacher model is DeepSeek R1, and the student model is Qwen-32B-Instruct trained with full parameter fine-tuning. While the student model continues to benefits from more SFT data from DeepSeek R1, a small amount of data, e.g., 16k is sufficient to significantly boost the average performance by 15.2%.

🔼 This figure demonstrates the impact of modifying the structure of reasoning steps in a Long Chain of Thought (Long CoT) on model performance. Three types of structural modifications were applied: deleting steps, inserting steps, and shuffling steps. The results show that altering the structure significantly reduces model accuracy, far more than changing the content within individual steps. This highlights the importance of maintaining logical flow and coherence in the reasoning process for effective performance. The figure visually represents the impact of these structural changes on the model’s ability to reason correctly.
read the caption
Figure 3: Reasoning step modifications. To evaluate perturbations to global structure across reasoning steps, we perform three modifications: deletion, insertion, and shuffling. These modifications break logical consistency across steps and degrade model accuracy far more than changes to local content within reasoning steps.

🔼 This figure demonstrates the effectiveness of Long Chain of Thought (Long CoT) fine-tuning across various language models. It compares the accuracy of several models (of different sizes and architectures) before and after fine-tuning using 17,000 samples from the R1-Preview dataset. The results show that fine-tuning with Long CoT data significantly improves the reasoning capabilities of most models, indicating the generalizability and benefits of this training approach.
read the caption
Figure 4: Generalization to other models. Accuracy for models of different sizes and architectures without SFT (green) and with SFT (blue). Most models show significant improvements when fine-tuned with 17k samples from R1-Preview, showing that the Long CoT fine-tuning is beneficial across models.
More on tables
| MATH500 | AIME24 | AMC23 | Olympiad. | Avg. | |
| Baselines | |||||
| Original | 84.8 | 16.7 | 67.5 | 47.6 | 56.7 |
| Correct | 89.2 | 40.0 | 77.5 | 58.5 | 66.3 |
| Content Modifications | |||||
| Wrong Answers | 88.6 | 30.0 | 77.5 | 56.1 | 63.1 |
| Corrupted Digits | |||||
| 100% | 5.4 | 0.0 | 2.5 | 2.8 | 2.7 |
| 70% | 85.6 | 30.0 | 77.5 | 54.8 | 62.0 |
| 50% | 87.6 | 36.7 | 77.5 | 55.0 | 64.2 |
| 20% | 88.4 | 30.0 | 82.5 | 57.2 | 64.5 |
| Removed keywords | |||||
| 100% | 86.6 | 33.3 | 77.5 | 54.4 | 63.0 |
| 50% | 87.6 | 36.7 | 82.5 | 56.7 | 65.9 |
| 20% | 87.2 | 33.3 | 72.5 | 56.1 | 62.3 |
| Structure Modifications | |||||
| Shuffled Steps | |||||
| 100% | 81.8 | 23.3 | 70.0 | 49.1 | 56.1 |
| 67% | 82.0 | 26.7 | 72.5 | 47.6 | 57.2 |
| 33% | 85.6 | 33.3 | 75.0 | 55.3 | 62.3 |
| Deleted Steps | |||||
| 100% | 79.2 | 13.3 | 60.0 | 45.4 | 49.5 |
| 67% | 84.2 | 26.7 | 55.0 | 48.1 | 53.5 |
| 33% | 88.2 | 23.3 | 80.0 | 57.7 | 62.3 |
| Inserted Steps | |||||
| 100% | 77.0 | 10.0 | 50.0 | 41.1 | 44.5 |
| 67% | 81.8 | 20.0 | 60.0 | 46.0 | 52.0 |
| 33% | 86.6 | 33.3 | 77.5 | 57.2 | 63.7 |
🔼 This table presents the results of experiments evaluating the impact of different types of perturbations on the performance of a large language model (LLM) during reasoning tasks. The LLM was fine-tuned on datasets containing various perturbations to the reasoning traces used for training. These perturbations fall into two categories: modifications to the content of individual reasoning steps (wrong answers, corrupted digits, and removed keywords) and modifications to the overall structure of the reasoning steps (deleted, inserted, or shuffled steps). The table shows the accuracy of the model on various mathematical reasoning benchmarks after training with each type of perturbation. The findings demonstrate that structural perturbations have a significantly more negative effect on the model’s accuracy compared to content perturbations.
read the caption
Table 2: Effect of trace perturbations on reasoning performance Section 4. All models are trained with base Qwen2.5-32B-Instruct. “Olympiad.” is short for “OlympiadBench”. In particular, we study (1) traces with modified reasoning step contents: wrong answers, corrupted digits, and removed reasoning keywords, and (2) traces with modified structure: deleted, inserted, or shuffled steps. We find that structural perturbations are far more detrimental to model accuracy than content perturbations.
| MMLU | ARC-C | IEval | MGSM | |
| Qwen2.5-32B-Inst. | 74.1 | 49.4 | 78.7 | 42.3 |
| QwQ | 71.2 | 49.7 | 42.5 | 19.1 |
| 17k R1 Samples | ||||
| SFT | 73.0 | 49.0 | 77.8 | 33.7 |
| LoRA (r=256) | 75.5 | 47.3 | 78.4 | 38.7 |
| 17k QwQ Samples | ||||
| SFT | 78.4 | 49.5 | 75.8 | 33.0 |
| LoRA (r=64) | 78.5 | 46.7 | 74.1 | 30.6 |
| 7k QwQ Samples | ||||
| SFT | 79.8 | 48.6 | 70.6 | 30.1 |
| LoRA (r=64) | 79.1 | 47.4 | 75.4 | 31.1 |
🔼 This table presents the performance of the Qwen-2.5-32B-Instruct model on various non-reasoning tasks before and after fine-tuning using data from the QwQ-32B-Preview model. It compares the model’s performance on benchmarks like MMLU (multi-task language understanding), ARC-C (science exam questions), IEval (instruction following), and MGSM (multilingual grade-school math problems). The purpose is to demonstrate that the fine-tuning process that improves reasoning capabilities does not significantly hurt performance on general language understanding and other tasks, indicating that the model retains its base capabilities after the fine-tuning process. The results show that the fine-tuned model generally maintains similar performance to the QwQ-32B-Preview on these tasks, demonstrating the success of the knowledge distillation method.
read the caption
Table 3: Distilled Model Performance on Non-Reasoning Tasks. The teacher model is QwQ-32B-Preview, and the student model is Qwen2.5-32B-Instruct. Compared to QwQ, distilled models retain most of the base model’s capabilities.
| Dataset | Original | Short CoT | Long CoT |
|---|---|---|---|
| Avg. output tokens | |||
| MATH500 | 684 | 515 | 3972 |
| AMC23 | 728 | 605 | 5037 |
| OlympiadBench | 1275 | 948 | 8616 |
| AIME24 | 825 | 687 | 15902 |
| Avg. keywords per response | |||
| MATH500 | 0.00 | 0.00 | 41.75 |
| AMC23 | 0.00 | 0.00 | 39.20 |
| OlympiadBench | 0.01 | 0.01 | 97.20 |
| AIME24 | 0.00 | 0.07 | 260.90 |
| Performance | |||
| MATH500 | 84.8 | 70.4 (-14.4) | 89.2 (+4.4) |
| AMC23 | 67.5 | 55.0 (-12.5) | 77.5 (+10.0) |
| OlympiadBench | 47.6 | 36.4 (-11.2) | 58.5 (+10.9) |
| AIME24 | 16.7 | 13.3 (-3.4) | 40.0 (+23.3) |
🔼 This table compares the number of output tokens and reasoning keywords used, as well as the model’s performance, when trained using short chain-of-thought (CoT) versus long chain-of-thought (CoT) reasoning. The base model used is Qwen2.5-32B-Instruct. The benchmarks are ordered from easiest to hardest, and the results show that the Long CoT model generates longer responses and uses more reasoning keywords as the difficulty of the problems increases. This suggests that the Long CoT training method enables the model to develop more sophisticated reasoning strategies.
read the caption
Table 4: Comparison of number of output tokens reasoning keywords, and the performance between training with Short or Long CoT. The original model is Qwen2.5-32B-Instruct. Benchmarks are ordered from easy to hard, where the model trained with Long CoT learns to produce longer CoTs and uses more keywords for harder problems.
| Dataset | 0% | 33% | 67% | 100% |
|---|---|---|---|---|
| Avg. output tokens | ||||
| Math | 3551 | 2979 | 2078 | 482 |
| AMC 2023 | 4838 | 6612 | 4623 | 609 |
| OlympiadBench | 7234 | 6802 | 4978 | 595 |
| AIME 2024 | 13088 | 11889 | 6798 | 620 |
| Avg. keywords per response | ||||
| Math | 32 | 28 | 20 | 0.017 |
| AMC 2023 | 39 | 85.6 | 77.8 | 0 |
| OlympiadBench | 77 | 70 | 56 | 0.009 |
| AIME 2024 | 143 | 143 | 90 | 0 |
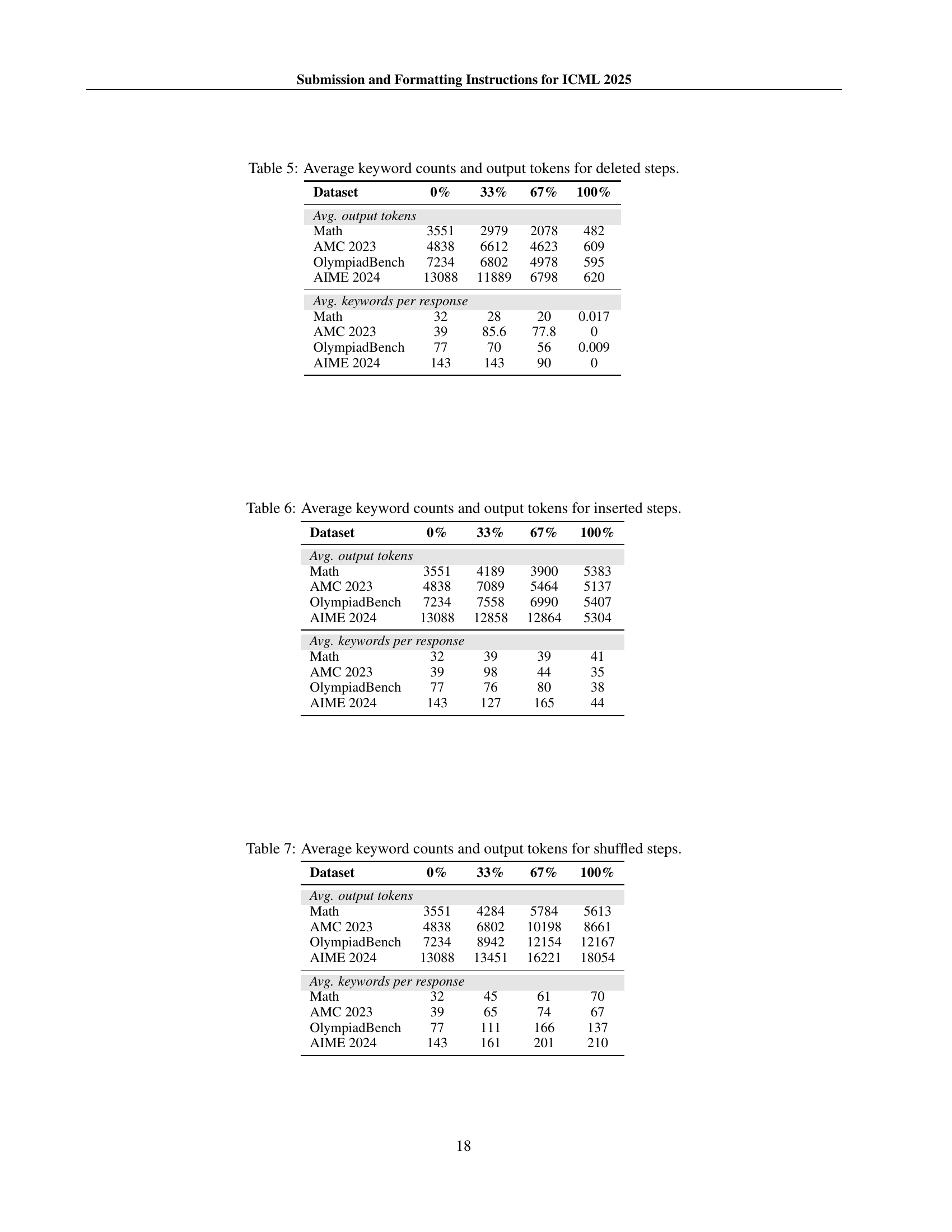
🔼 This table presents the average number of keywords and output tokens used in model responses when training data with deleted reasoning steps is used. The data is broken down by dataset (Math, AMC 2023, OlympiadBench, AIME 2024) and the percentage of deleted steps (0%, 33%, 67%, 100%). This allows for the analysis of how the removal of reasoning steps impacts the model’s output length and use of reasoning keywords.
read the caption
Table 5: Average keyword counts and output tokens for deleted steps.
| Dataset | 0% | 33% | 67% | 100% |
|---|---|---|---|---|
| Avg. output tokens | ||||
| Math | 3551 | 4189 | 3900 | 5383 |
| AMC 2023 | 4838 | 7089 | 5464 | 5137 |
| OlympiadBench | 7234 | 7558 | 6990 | 5407 |
| AIME 2024 | 13088 | 12858 | 12864 | 5304 |
| Avg. keywords per response | ||||
| Math | 32 | 39 | 39 | 41 |
| AMC 2023 | 39 | 98 | 44 | 35 |
| OlympiadBench | 77 | 76 | 80 | 38 |
| AIME 2024 | 143 | 127 | 165 | 44 |
🔼 This table presents the average number of keywords and output tokens used in model responses when reasoning steps are inserted into the training data. It shows the impact of inserting 33%, 67%, and 100% of randomly selected reasoning steps from other correct samples on various math and coding benchmarks (Math, AMC 2023, OlympiadBench, AIME 2024). The comparison is made against a baseline where no steps are inserted (0%). This helps to analyze how structural changes affect the model’s reasoning performance and language use.
read the caption
Table 6: Average keyword counts and output tokens for inserted steps.
| Dataset | 0% | 33% | 67% | 100% |
|---|---|---|---|---|
| Avg. output tokens | ||||
| Math | 3551 | 4284 | 5784 | 5613 |
| AMC 2023 | 4838 | 6802 | 10198 | 8661 |
| OlympiadBench | 7234 | 8942 | 12154 | 12167 |
| AIME 2024 | 13088 | 13451 | 16221 | 18054 |
| Avg. keywords per response | ||||
| Math | 32 | 45 | 61 | 70 |
| AMC 2023 | 39 | 65 | 74 | 67 |
| OlympiadBench | 77 | 111 | 166 | 137 |
| AIME 2024 | 143 | 161 | 201 | 210 |
🔼 This table presents the average number of reasoning keywords and the average number of output tokens generated by the model when the order of reasoning steps in the training data is randomly shuffled. It shows how the model’s performance changes as the percentage of shuffled steps increases (33%, 67%, and 100%), comparing these results against a baseline with no shuffled steps (0%). The data is broken down by dataset (Math, AMC 2023, OlympiadBench, and AIME 2024) to highlight variations in performance across different problem types.
read the caption
Table 7: Average keyword counts and output tokens for shuffled steps.
Full paper#