TL;DR#
Linear attention offers advantages in sequence modeling, but existing sequence parallelism (SP) methods have limitations. They are not optimized for linear attention’s structure or use inefficient communication strategies, hindering scalability for long sequences in distributed systems. This leads to lower computation parallelism and increased training time.
LASP-2 tackles these issues by rethinking the minimal communication requirement for SP. It reorganizes the communication-computation workflow, needing only one AllGather operation on intermediate memory states (independent of sequence length). This significantly improves both communication and computation parallelism and their overlap. LASP-2H extends this to hybrid models (linear and standard attention). Evaluations show LASP-2 achieves a 15.2% speedup over LASP and 36.6% over Ring Attention with a 2048K sequence length on 64 GPUs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large language models and linear attention mechanisms. It presents LASP-2, a novel sequence parallelism method that significantly improves the training speed and scalability of these models, addressing a key challenge in handling very long sequences. This work directly impacts the efficiency and resource consumption of large-scale model training, opening new avenues for further research in optimizing training processes and enhancing the capabilities of next-generation language models.
Visual Insights#

🔼 This figure illustrates how LASP-2 handles sequence parallelism with masking, a crucial aspect of autoregressive tasks. It shows the decomposition of computations into intra-chunk (within a single chunk) and inter-chunk (between multiple chunks) operations. The colored chunks highlight the inter-chunk computations, which are performed independently and in parallel across different devices because they don’t depend on the results of other chunks. This parallel processing improves efficiency. The intra-chunk computations, on the other hand, involve sequential operations due to the masking requirements of autoregressive tasks. The figure visually demonstrates how LASP-2 efficiently combines parallel and sequential processing to improve the scalability of linear attention models with masking.
read the caption
Figure 1: Computation Decomposition in LASP-2 with masking. Colored chunks represent inter-chunks.
| Indices | Operations | ||
| Any indices | (or omitted) | Matrix multiplication | |
| Index of current token | Hadamard multiplication | ||
| Index of chunk | Vectors and Matrices | ||
| Constants | , | Input and output vectors | |
| Hidden dimension | , , | Query, key, value vectors | |
| World size | , | Input and output matrices | |
| Sequence length | , , | Query, key, value matrices | |
| Total number of chunks | Memory state matrix | ||
| Chunk length | , , | Weight matrices |
🔼 This table lists the notations used throughout the paper, clarifying the meaning of indices, mathematical operations, constants, vectors, and matrices. It serves as a reference for understanding the symbols and their representations within the mathematical formulas and algorithms presented in the paper.
read the caption
Table 1: Notations. Indices, operations, constants, vectors and matrices used in the paper.
In-depth insights#
Linear Attention SP#
Sequence parallelism (SP) for linear attention mechanisms presents unique challenges and opportunities. Linear attention’s inherent computational efficiency, unlike standard attention, offers a compelling foundation for scaling to longer sequences. However, naive SP approaches may not fully leverage this efficiency, leading to suboptimal speedups. Effective SP methods must carefully consider the communication patterns required to aggregate intermediate results across multiple devices. Minimizing communication overhead is paramount; strategies like all-gather operations (as explored in LASP-2), which aggregate results efficiently, rather than ring-based approaches, are crucial. Balancing communication and computation is key. Carefully designed SP algorithms can ensure sufficient overlap between communication and computation, leading to significant improvements in training throughput. Hybrid models, incorporating both linear and standard attention, present further complexities that demand tailored SP approaches, such as the unified all-gather design in LASP-2H. Evaluating the scalability of different SP techniques across various sequence lengths and hardware configurations is also crucial to understanding their practical limitations and optimal deployment strategies. The success of linear attention SP hinges on efficiently managing communication and harnessing the inherent computational advantages of linear attention, leading to more efficient and scalable training of large language models.
LASP-2 Algorithm#
The LASP-2 algorithm presents a refined approach to sequence parallelism (SP) in linear attention models. Its core innovation lies in rethinking minimal communication requirements, moving from a ring-style communication to a single all-gather collective communication operation. This shift dramatically improves both communication and computation parallelism, especially for longer sequences. The algorithm’s efficiency stems from its independent sequence length memory states for the all-gather operation and an optimized workflow that minimizes redundant computation and improves communication-computation overlap. LASP-2’s extension to hybrid models (LASP-2H) further enhances its applicability by applying the same efficient communication strategy to standard attention layers, offering a unified and efficient solution for blended models. Key advantages include reduced communication costs, superior throughput, and improved scalability compared to previous methods. The algorithm’s design considers both autoregressive and bidirectional tasks, handling masking effectively for each.
Hybrid Model SP#
The concept of ‘Hybrid Model SP’ in the context of large language models (LLMs) and sequence parallelism (SP) refers to optimizing parallel processing techniques for models that combine both linear and standard attention mechanisms. Linear attention offers advantages in terms of speed and memory efficiency over the quadratic complexity of standard attention, but it may struggle with certain tasks. Standard attention, while computationally expensive, excels in tasks demanding high recall. A hybrid model leverages the strengths of both approaches. The challenge in ‘Hybrid Model SP’ lies in efficiently parallelizing the distinct computational workflows of linear and standard attention. LASP-2H, as described in the paper, attempts to resolve this by using a unified all-gather communication strategy for both. This approach aims to minimize communication overhead and maximize overlap between communication and computation, leading to significant speed improvements in training compared to traditional methods such as ring-based communication. The effectiveness of this unified approach hinges on the ability to seamlessly integrate the communication patterns of both attention types, thereby avoiding performance bottlenecks in either linear or standard components. The success of this strategy will determine the efficacy of ‘Hybrid Model SP’ as a practical method for scaling long-context LLMs.
Scalability Analysis#
A robust scalability analysis of a large language model (LLM) should go beyond simply reporting throughput numbers. It must delve into the trade-offs between throughput, memory usage per GPU, and the number of GPUs used. The analysis needs to explore how the model’s performance changes as these factors are scaled. For example, it’s crucial to investigate whether the improvements in throughput are linear or sublinear with increasing GPU count, and what the corresponding memory footprint implications are. A strong analysis would also consider the communication overhead inherent in distributed training, examining its impact on overall scalability. Investigating how the communication cost scales with the sequence length and the number of GPUs is essential for understanding the true scalability limitations. Furthermore, the impact of different attention mechanisms on scalability should be assessed. The analysis should discuss whether linear attention, compared to standard attention, exhibits superior scalability, and if so, under which conditions. Finally, the analysis should evaluate the stability and reliability of the scaling across different hardware and software configurations, emphasizing any potential bottlenecks or limitations.
Future Directions#
Future research directions stemming from the LASP-2 paper could explore several promising avenues. Extending LASP-2H to more complex hybrid architectures that incorporate diverse attention mechanisms beyond standard and linear attention is crucial. This would involve investigating the optimal interplay between different attention types for various tasks and sequence lengths. A detailed empirical study comparing LASP-2’s performance across different hardware platforms and network topologies would enhance its practical applicability and reveal potential bottlenecks. Investigating adaptive or dynamic sequence partitioning strategies within LASP-2, adjusting chunk sizes based on the sequence’s inherent properties or computational demands, could further improve efficiency. Finally, exploring the integration of LASP-2 with other optimization techniques, such as quantization and pruning, promises significant performance gains. These advancements will solidify LASP-2’s position as a leading technology for large-scale sequence processing and will enable more computationally intensive tasks in various domains.
More visual insights#
More on figures

🔼 Figure 2 illustrates the LASP-2H approach applied to a hybrid model containing both linear and standard attention layers. The diagram showcases two dimensions of parallelism: Tensor Parallelism (TP) and Sequence Parallelism (SP), each split into two parts. Communication patterns, whether all-gather (AG), reduce-scatter (RS), or no-operation (No-op), are indicated for both forward and backward passes. The key difference highlighted is that Sequence Parallelism in linear attention layers operates on memory states (Mt) of dimensions d x d, whereas in standard attention, it operates on key (Kt) and value (Vt) states of dimensions C x d. The colors yellow and green distinguish between TP and SP communication operations respectively.
read the caption
Figure 2: Visualization of LASP-2H on Linear Attention and Standard Attention hybrid model. We exemplify LASP-2H on the hybrid layers of linear attention and standard attention modules with both TP and SP (both have a dimension of 2). The communication operations colored in yellow and green are for TP and SP, respectively. AG/RS: all-gather in forward and reduce-scatter in backward, and vice versa. AG/No: all-gather in forward and no-op in backward, and vice versa. Note that the SP communication operations for linear attention operate on the memory state 𝐌t∈ℝd×dsubscript𝐌𝑡superscriptℝ𝑑𝑑\mathbf{M}_{t}\in\mathbb{R}^{d\times d}bold_M start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_d × italic_d end_POSTSUPERSCRIPT, while for standard attention, they operate on states 𝐊t,𝐕t∈ℝC×dsubscript𝐊𝑡subscript𝐕𝑡superscriptℝ𝐶𝑑\mathbf{K}_{t},\mathbf{V}_{t}\in\mathbb{R}^{C\times d}bold_K start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , bold_V start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT italic_C × italic_d end_POSTSUPERSCRIPT.

🔼 Figure 3 presents a performance comparison of different sequence parallelism (SP) methods for training a large language model (LLM). The experiment uses a Linear-Llama3-1B model, a variant of the Llama3 model where standard attention is replaced with basic linear attention, making the training time linear with sequence length. A total of 64 A100 GPUs were used in parallel to accelerate training. The SP size (T) was set to 64, and to enable training with very-long sequences (up to 2048K tokens), the batch size was maintained at 1. The plot displays the throughput (tokens/second) of LASP-2 against other methods such as Megatron-SP, Ring Attention, and LASP-1, across a range of sequence lengths. The results demonstrate the superior speed and scalability of LASP-2, particularly as sequence lengths increase beyond 64K tokens.
read the caption
Figure 3: Speed Comparison (tokens/s). Experiments were carried out on a pure Linear-Llama3-1B model, utilizing the basic linear attention module. A total of 64 A100 GPUs were employed, and the SP size T𝑇Titalic_T was also set to 64. To accommodate very-long sequence lengths, such as 2048K, the batch size was kept fixed at 1 throughout this experiment.
More on tables
| Model | SP Method | Attention Module | Pure Model | Hybrid Model | ||
| Thpt | Loss | Thpt | Loss | |||
| Llama3 | Ring Attention | Standard Attention | 16549.5 | 2.759 | ||
| Linear-Llama3 | LASP-2(H) | Basic Linear Attention | 17834.3 | 2.892 | 17394.7 | 2.824 |
| Lightning Attention | 17926.1 | 2.862 | 17384.2 | 2.758 | ||
| Retention | 17859.6 | 2.867 | 17352.5 | 2.759 | ||
| GLA | 17785.3 | 2.845 | 17273.2 | 2.754 | ||
| Based | 17946.1 | 2.754 | 17462.5 | 2.751 | ||
| Rebased | 17896.2 | 2.845 | 17284.5 | 2.787 | ||
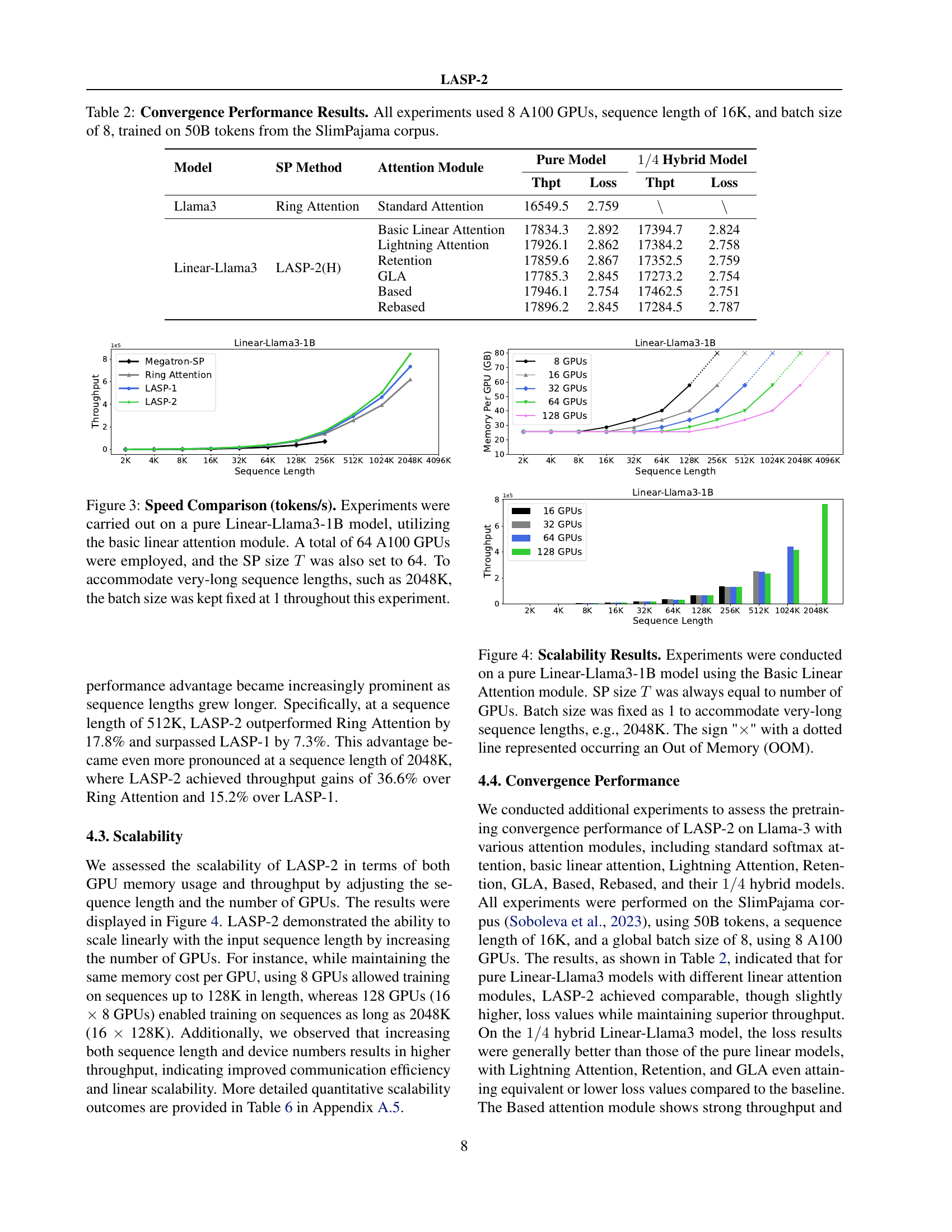
🔼 This table presents the convergence performance results of different models trained using various sequence parallelism methods. The models were trained on 50 billion tokens from the SlimPajama corpus using 8 A100 GPUs, a sequence length of 16,000 tokens, and a batch size of 8. The table compares the throughput (tokens per second) and loss for pure linear models and 1/4 hybrid models (combining linear and standard attention layers) using different attention mechanisms and sequence parallelism methods. The results show the training efficiency and convergence properties of each configuration.
read the caption
Table 2: Convergence Performance Results. All experiments used 8 A100 GPUs, sequence length of 16K, and batch size of 8, trained on 50B tokens from the SlimPajama corpus.
| Model | Training Loss | Validation Loss |
| RoBERTa Baseline (Ring Attention) | 1.815 | 1.957 |
| RoBERTa with Basic Linear Attention (LASP-2) | 1.813 | 1.957 |
🔼 This table presents the training and validation loss values achieved during bidirectional language modeling experiments using different model configurations. The results demonstrate the performance of the ROBERTa baseline model (with Ring Attention) compared to a model employing the Basic Linear Attention mechanism and the LASP-2 technique.
read the caption
Table 3: Convergence Performance on Bidirectional Language Modeling Task. Both training and validation loss values are reported.
| Linear Sequence Modeling Module | 0 Hybrid (Pure Linear Model) | 1/8 Hybrid | 1/4 Hybrid | 1/2 Hybrid |
| Basic Linear Attention | 2.892 | 2.826 | 2.824 | 2.775 |
| Lightning Attention | 2.848 | 2.756 | 2.750 | 2.742 |
| Retention | 2.855 | 2.757 | 2.758 | 2.748 |
| GLA | 2.845 | 2.751 | 2.754 | 2.753 |
🔼 This table presents the results of an ablation study conducted to evaluate the impact of varying the ratio of linear and standard attention layers in hybrid models. The study measures the loss values achieved by different model configurations. Specifically, it compares models with various ratios of linear to standard attention layers (0%, 12.5%, 25%, and 50%). The performance is analyzed for different linear attention mechanisms (Basic Linear Attention, Lightning Attention, Retention, and GLA). Note that pure linear models (0% hybrid ratio) use the LASP-2 algorithm for sequence parallelism, while hybrid models utilize the LASP-2H algorithm.
read the caption
Table 4: Ablation Study on Hybrid Ratio in Hybrid Models. Loss values are reported in the Table. Note that pure linear models use LASP-2, while hybrid models use LASP-2H.
| Split Size of Gathering | 2048 | 512 | 128 | 32 |
| Number of Splits | 1 | 4 | 16 | 64 |
| Throughput | 486183 | 486166 | 486169 | 486158 |
🔼 This table presents the throughput (tokens per second) achieved by LASP-2 on the Linear-Llama3-1B model with varying split sizes for gathering memory states. The experiment uses a model with 16 attention heads and a hidden dimension of 2048. Different split sizes correspond to different numbers of parallel operations during the all-gather communication. The results showcase the impact of altering the parallelism level on the overall model performance.
read the caption
Table 5: Throughput Results (tokens/sec) on Varying Split Sizes of Gathering. Linear-Llama3-1B model (with 16 heads and hidden dimension of 2048) is used.
| Sequence Length | Number of GPUs | Throughput | Memory Usage Per GPU |
| 2K | 16 | 1254 | 25.6 |
| 32 | 1209 | 25.6 | |
| 64 | 1285 | 25.6 | |
| 128 | 1205 | 25.6 | |
| 4K | 16 | 2478 | 25.6 |
| 32 | 2446 | 25.6 | |
| 64 | 2327 | 25.6 | |
| 128 | 2344 | 25.6 | |
| 8K | 16 | 4835 | 25.6 |
| 32 | 4784 | 25.6 | |
| 64 | 4693 | 25.6 | |
| 128 | 4678 | 25.6 | |
| 16K | 16 | 9530 | 25.6 |
| 32 | 9494 | 25.6 | |
| 64 | 9305 | 25.6 | |
| 128 | 9313 | 25.6 | |
| 32K | 16 | 18105 | 28.7 |
| 32 | 17755 | 25.6 | |
| 64 | 17835 | 25.6 | |
| 128 | 17807 | 25.6 | |
| 64K | 16 | 35507 | 33.8 |
| 32 | 34240 | 28.7 | |
| 64 | 34118 | 25.6 | |
| 128 | 33344 | 25.6 | |
| 128K | 16 | 68406 | 40.2 |
| 32 | 68545 | 33.8 | |
| 64 | 67344 | 28.7 | |
| 128 | 66811 | 25.6 | |
| 256K | 16 | 135635 | 57.8 |
| 32 | 132605 | 40.2 | |
| 64 | 130215 | 33.8 | |
| 128 | 131550 | 28.7 | |
| 512K | 16 | OOM | OOM |
| 32 | 250586 | 57.8 | |
| 64 | 245353 | 40.2 | |
| 128 | 233442 | 33.8 | |
| 1024K | 16 | OOM | OOM |
| 32 | OOM | OOM | |
| 64 | 442221 | 57.8 | |
| 128 | 416465 | 40.2 | |
| 2048K | 16 | OOM | OOM |
| 32 | OOM | OOM | |
| 64 | OOM | OOM | |
| 128 | 769030 | 57.8 | |
| 4096K | 16 | OOM | OOM |
| 32 | OOM | OOM | |
| 64 | OOM | OOM | |
| 128 | OOM | OOM |
🔼 This table presents the scalability results of LASP-2, showing its throughput (tokens per second) and GPU memory usage (in GB) at various sequence lengths (from 2K to 4096K) and with different numbers of GPUs. It demonstrates how the performance of LASP-2 scales with increased sequence length and GPU resources. The results are based on the Linear-Llama3-1B model.
read the caption
Table 6: Quantitative Scalability Results of LASP-2 on Throughput (tokens/sec) and Memory Usage Per GPU (GB). Experiments are performed on Linear-Llama3-1B, scaling sequence length from 2K to 4096K.
Full paper#