MRS: A Fast Sampler for Mean Reverting Diffusion based on ODE and SDE Solvers

2502.07856

Ao Li et el.

🤗 2025-02-17

TL;DR
#

Current methods for controllable image generation using diffusion models often involve modifying the score function or require extensive training. However, Mean Reverting Diffusion (MR Diffusion) offers a more straightforward approach by modifying the SDE structure, yet suffers from slow sampling speed. This necessitates hundreds of function evaluations (NFEs) for high-quality image generation, hindering practical applications.

This research introduces MRS (MR Sampler), a novel algorithm that significantly accelerates the sampling of MR Diffusion. MRS achieves this acceleration by solving the reverse-time stochastic differential equation (SDE) and the probability flow ordinary differential equation (PF-ODE) associated with MR Diffusion to derive semi-analytical solutions. These solutions combine analytical functions with an integral approximated by a neural network, enabling high-quality sample generation in far fewer steps (10-20 times faster). The algorithm also supports various network parameterizations, proving effective and adaptable across numerous image restoration tasks.

Key Takeaways
#

Why does it matter?
#

This paper is important because it significantly accelerates the sampling process of Mean Reverting Diffusion (MR Diffusion) models, a powerful class of generative models for controllable image generation. This acceleration makes MR Diffusion far more practical for real-world applications, opening up new avenues for research in controllable image generation and solving inverse problems. The introduction of a novel, training-free algorithm that is both faster and more adaptable to various neural network architectures is a significant advancement.

Visual Insights
#

🔼 This figure presents a qualitative comparison of image generation results using two different sampling methods: MR Sampler and Posterior Sampling. Both methods utilize a pre-trained Mean Reverting Diffusion model (Luo et al., 2024a). The comparison showcases the visual quality of images generated at varying numbers of function evaluations (NFEs). The top row shows results from dehazing, and the bottom row displays results from image inpainting. Both tasks use images from two distinct datasets: RESIDE-6k (Qin et al., 2020b) and CelebA-HQ (Karras, 2017). The ground truth images are provided for reference, allowing for direct visual comparison of the generated samples with the original images.
read the caption
Figure 1: Qualitative comparisons between MR Sampler and Posterior Sampling. All images are generated by sampling from a pre-trained MR Diffusion (Luo et al., 2024a) on the RESIDE-6k (Qin et al., 2020b) dataset and the CelebA-HQ (Karras, 2017) dataset.

SDE	$f(t)$	$g(t)$	$m(t)$	$v(t)$
VPSDE(Ho et al., 2020)	$-\frac{1}{2}\beta(t)$	$\sqrt{\beta(t)}$	$\bm{x}_{0}e^{-\frac{1}{2}\int_{0}^{t}\beta(\tau)\mathrm{d}\tau}$	$\bm{I}-\bm{I}e^{-\int_{0}^{t}\beta(\tau)\mathrm{d}\tau}$
VESDE(Song & Ermon, 2019)	$0$	$\sqrt{\frac{\mathrm{d}[\sigma^{2}(t)]}{\mathrm{d}t}}$	$\bm{x}_{0}$	$\left[\sigma^{2}(t)-\sigma^{2}(0)\right]\bm{I}$

🔼 This table compares two popular stochastic differential equations (SDEs) used in diffusion probabilistic models: Variance Preserving SDE (VPSDE) and Variance Exploding SDE (VESDE). For each SDE, it lists the functions defining the drift and diffusion coefficients, as well as the resulting mean 𝑚(𝑡) and variance 𝑣(𝑡) of the transition probability distribution 𝑝(𝒙𝑡|𝒙0) at time t, given an initial state 𝒙0. This information is crucial for understanding how each SDE models the diffusion process and the properties of the resulting probability distributions.
read the caption
Table 1: Two popular SDEs, Variance Preserving SDE (VPSDE) and Variance Exploding SDE (VESDE). m⁢(t)𝑚𝑡m(t)italic_m ( italic_t ) and v⁢(t)𝑣𝑡v(t)italic_v ( italic_t ) refer to mean and variance of the transition probability p⁢(𝒙t|𝒙0)𝑝conditionalsubscript𝒙𝑡subscript𝒙0p(\bm{x}_{t}|\bm{x}_{0})italic_p ( bold_italic_x start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT | bold_italic_x start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ).

In-depth insights
#

ODE/SDE Solvers
#

The effectiveness of diffusion models heavily relies on the efficiency of their sampling process. ODE (Ordinary Differential Equation) and SDE (Stochastic Differential Equation) solvers play a crucial role in this regard. The core idea involves transforming the complex sampling process from a stochastic diffusion into a deterministic or semi-deterministic trajectory. This transformation allows for faster convergence and reduces the computational cost associated with traditional methods, which often require hundreds or even thousands of function evaluations. The choice between ODE and SDE solvers influences the accuracy and stability of the sampling process. ODE solvers provide deterministic solutions, often more stable for simpler diffusion models. SDE solvers, while introducing stochasticity, are capable of handling more complex scenarios and can offer higher accuracy when appropriately implemented. The selection of specific ODE/SDE solvers and their corresponding numerical methods (e.g., Euler-Maruyama, higher-order methods) significantly impacts the overall computational efficiency and the quality of generated samples. The development of advanced, tailored ODE/SDE solvers remains a critical area of research to further improve the speed and stability of diffusion models and to extend their applicability to increasingly complex generative tasks.

MRS Sampler
#

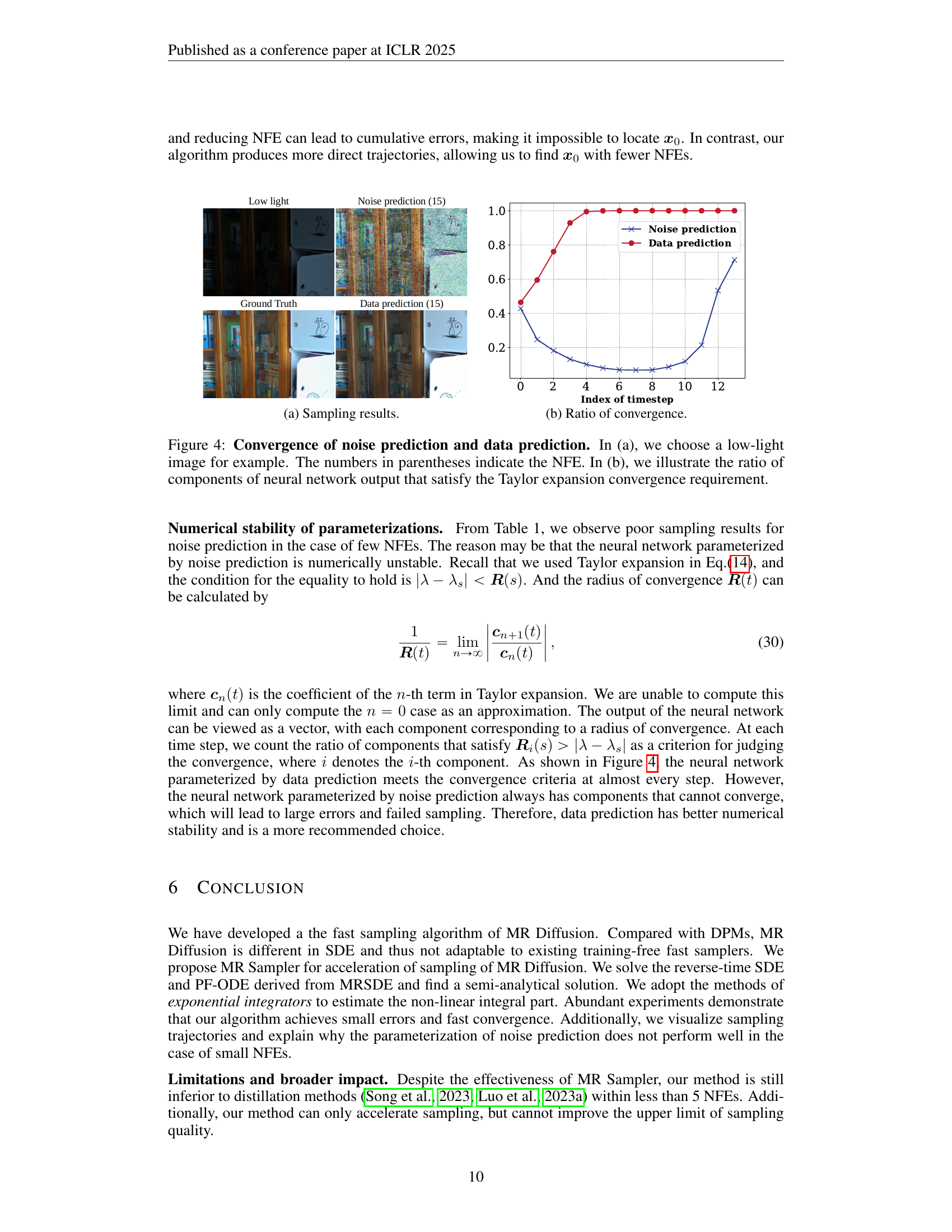
The proposed “MRS Sampler” algorithm offers a significant advancement in sampling efficiency for mean-reverting diffusion models. Its core innovation lies in deriving semi-analytical solutions for both the reverse-time stochastic differential equation (SDE) and the probability flow ordinary differential equation (PF-ODE). This approach, unlike prior methods, avoids relying solely on numerical approximations, leading to a substantial speedup (10-20x) while maintaining high sampling quality. The algorithm’s flexibility is noteworthy, as it supports various parameterizations (noise, data, velocity prediction), providing adaptability across different image restoration tasks and training objectives. Data prediction parameterization is highlighted for its superior numerical stability, particularly with lower numbers of function evaluations (NFEs). Ultimately, MRS Sampler presents a practical solution to overcome the computational bottleneck of MR diffusion, paving the way for wider applicability in controllable generation.

Data Prediction
#

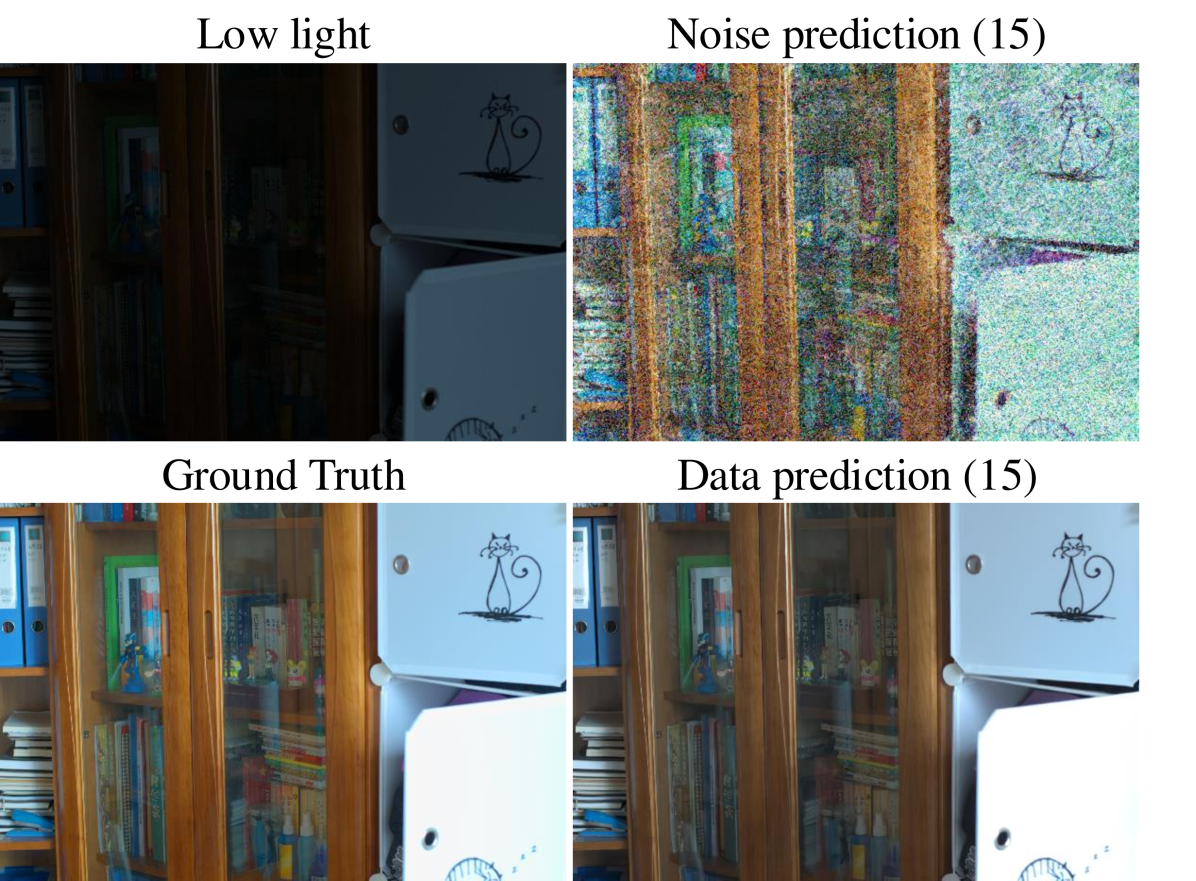
The concept of ‘data prediction’ within the context of diffusion probabilistic models, specifically in relation to the presented Mean Reverting Diffusion (MRD) sampler, represents a significant advancement in sampling stability. Unlike noise prediction, which focuses on predicting the noise added during the forward diffusion process, data prediction directly targets the original data. This approach offers enhanced numerical stability, particularly crucial when dealing with a limited number of function evaluations (NFEs). The inherent characteristic of data prediction, confined within the bounds of [-1,1], prevents the neural network’s output from exhibiting excessive fluctuations, especially important during early sampling stages where approximation errors can accumulate. This stability translates directly to improved sampling quality with fewer sampling steps, as demonstrated by the significant speedup achieved by the MR Sampler using data prediction compared to noise prediction. The superior numerical stability of data prediction, therefore, is a key factor contributing to the efficiency and effectiveness of the proposed MR Sampler.

Numerical Stability
#

The section on numerical stability highlights a critical weakness of noise prediction methods in diffusion models, especially at low numbers of function evaluations (NFEs). Noise prediction’s reliance on Taylor expansion introduces significant instability, as evidenced by the narrow convergence domains and even complete failure to converge in some cases. This is contrasted sharply with data prediction, which exhibits superior numerical stability across a wider range of NFEs. The instability stems from the neural network’s difficulty in accurately predicting noise values, especially when those values fall outside its training distribution. The authors quantify this instability by assessing the proportion of neural network components meeting the convergence criteria, demonstrating the clear advantage of the data prediction approach. This finding underscores the importance of considering the numerical properties of different parameterization methods when designing fast sampling algorithms for diffusion models, especially when aiming for high speedup factors at low NFEs. The implications extend beyond this specific model, suggesting a more careful consideration of numerical stability is warranted when adopting or developing any training-free diffusion model sampling technique.

Future Work
#

The ‘Future Work’ section of this research paper could explore several promising avenues. Extending MRSampler to handle more complex SDEs beyond the mean-reverting type would significantly broaden its applicability. This might involve developing novel numerical techniques or adapting existing methods to address the increased challenges in solving these more intricate equations. Another crucial area for future research is improving the numerical stability of the noise prediction method, especially at low NFEs. Investigating alternative neural network architectures or training strategies could enhance robustness and potentially unlock superior performance at fewer sampling steps. Investigating the theoretical properties of MRSampler and formalizing the conditions under which its semi-analytical solutions converge and achieve high sampling quality is also essential. This would enhance the trustworthiness and expand the understanding of the algorithm’s capabilities. Finally, a comparative analysis against other state-of-the-art diffusion samplers under various conditions and image restoration tasks would provide a strong benchmark, enabling more accurate assessment of the algorithm’s performance and identifying its relative strengths and limitations.

More visual insights
#

More on figures

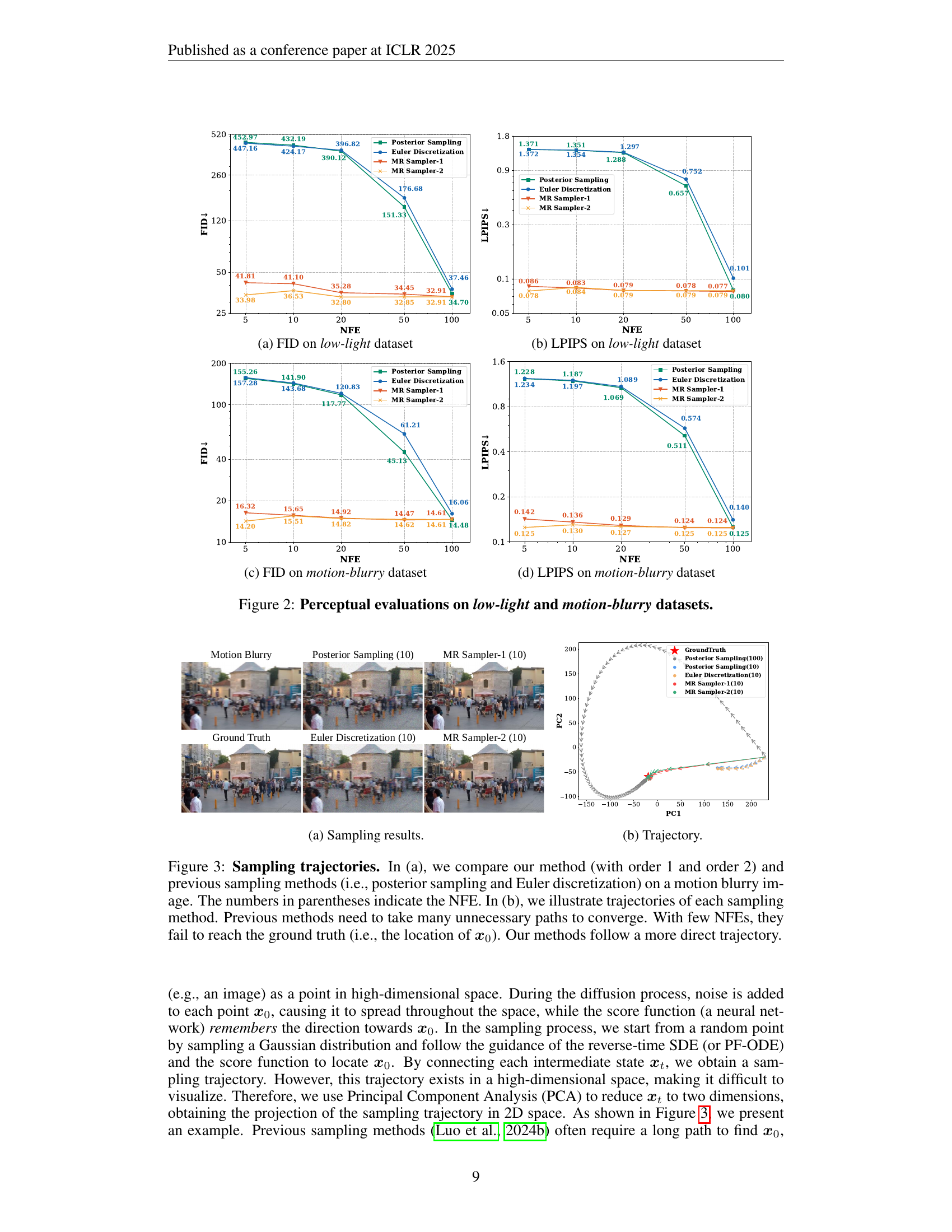
🔼 The figure shows the FID (Fréchet Inception Distance) scores for different numbers of function evaluations (NFEs) on a low-light image denoising task. FID is a metric used to evaluate the quality of generated images, with lower scores indicating better image quality. The figure compares the FID scores of the proposed MR Sampler (a fast sampler for Mean Reverting Diffusion) against those of posterior sampling and Euler discretization, two standard sampling methods for diffusion models. The results demonstrate that the MR Sampler achieves comparable image quality to posterior sampling and Euler discretization while using significantly fewer NFEs, highlighting its efficiency in image generation.
read the caption
(a) FID on low-light dataset

🔼 This figure shows a graph of the Learned Perceptual Image Patch Similarity (LPIPS) metric against the number of function evaluations (NFEs) for a low-light image restoration task. The LPIPS metric measures the perceptual difference between a generated image and a ground truth image. The graph compares different sampling methods: Posterior Sampling, Euler Discretization, and two versions of the MR Sampler (MR Sampler-1 and MR Sampler-2). It illustrates how the perceptual quality of the generated images improves with an increasing number of NFEs for each method and that MR Sampler-2 achieves a lower LPIPS score, thus higher image quality, faster than other methods.
read the caption
(b) LPIPS on low-light dataset

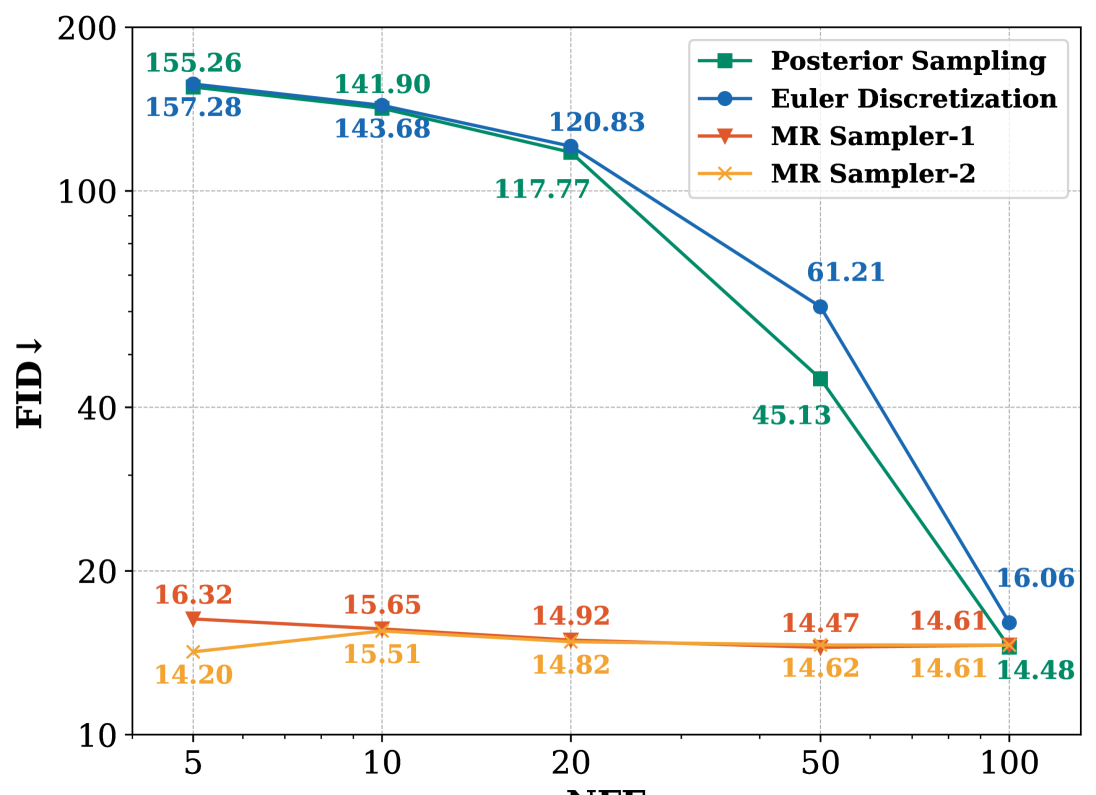
🔼 This figure shows the Fréchet Inception Distance (FID) scores for different numbers of function evaluations (NFEs) on a motion-blurry dataset. Lower FID scores indicate better image quality. The figure compares the performance of four different sampling methods: Posterior Sampling, Euler Discretization, MR Sampler-1, and MR Sampler-2. The x-axis shows the number of NFEs, and the y-axis shows the FID score. The figure demonstrates the impact of the number of NFEs on the FID score for each sampling method, allowing for a comparison of their efficiency and effectiveness.
read the caption
(c) FID on motion-blurry dataset

🔼 This plot presents the Linearly Perceptually-Inspired Image Patch Similarity (LPIPS) scores for different numbers of function evaluations (NFEs) on a motion-blurry image dataset. LPIPS measures the perceptual similarity between a generated image and the ground truth. Lower scores indicate higher perceptual similarity, showing how well the model reconstructs the image. The plot shows that as the number of NFEs increases, the LPIPS score generally decreases, indicating that the sampling process produces images that are more similar to the ground truth.
read the caption
(d) LPIPS on motion-blurry dataset

🔼 Figure 2 presents quantitative results of perceptual evaluations performed on two specific image restoration tasks: low-light and motion-blurry image datasets. The figure displays the LPIPS (Learned Perceptual Image Patch Similarity) and FID (Fréchet Inception Distance) scores, along with PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity Index) scores, obtained using four different sampling methods: Posterior Sampling, Euler Discretization, and two variants of the proposed MR Sampler (MR Sampler-1 and MR Sampler-2). These scores are presented for various NFEs (Number of Function Evaluations), illustrating the impact of the number of sampling steps on image quality and showing that the MR Sampler methods achieve better performance with fewer sampling steps.
read the caption
Figure 2: Perceptual evaluations on low-light and motion-blurry datasets.

🔼 This table presents the results of an ablation study comparing the performance of two different neural network parameterizations used in the MR Sampler algorithm for image restoration. The study focuses on the Rain100H dataset, a benchmark dataset for image restoration tasks involving rain streaks. The two parameterizations being compared are noise prediction and data prediction. The table shows how performance metrics (LPIPS, FID, PSNR, and SSIM) vary with different numbers of function evaluations (NFEs), which are an indication of the computational cost of the algorithm. This analysis helps determine which parameterization strategy is more effective and stable in the context of MR Diffusion models.
read the caption
Table 2: Ablation study of network parameterizations on the Rain100H dataset.

🔼 This table presents the results of an ablation study comparing two different solver types (ODE and SDE) used within the MR Sampler algorithm. The study focuses on the CelebA-HQ dataset, a benchmark for image generation, and evaluates the performance of each solver type in terms of LPIPS, FID, PSNR, and SSIM. These metrics assess the quality and efficiency of image generation using the MR Sampler algorithm. The table shows these scores with varying numbers of function evaluations (NFE) for each solver type, allowing for a detailed comparison of their performance across different computational budgets.
read the caption
Table 3: Ablation study of solver types on the CelebA-HQ dataset.

🔼 The figure shows a comparison of sampling results from different methods on a motion-blurry image. The methods include posterior sampling, Euler discretization, and two variants of the proposed MR Sampler (order 1 and order 2). Each method’s results are shown at different NFEs (Number of Function Evaluations) ranging from 5 to 100. The ground truth image is also provided for comparison. The image illustrates how the different methods progress over iterations in approaching the ground truth image, highlighting the efficiency and accuracy differences among them.
read the caption
(a) Sampling results.

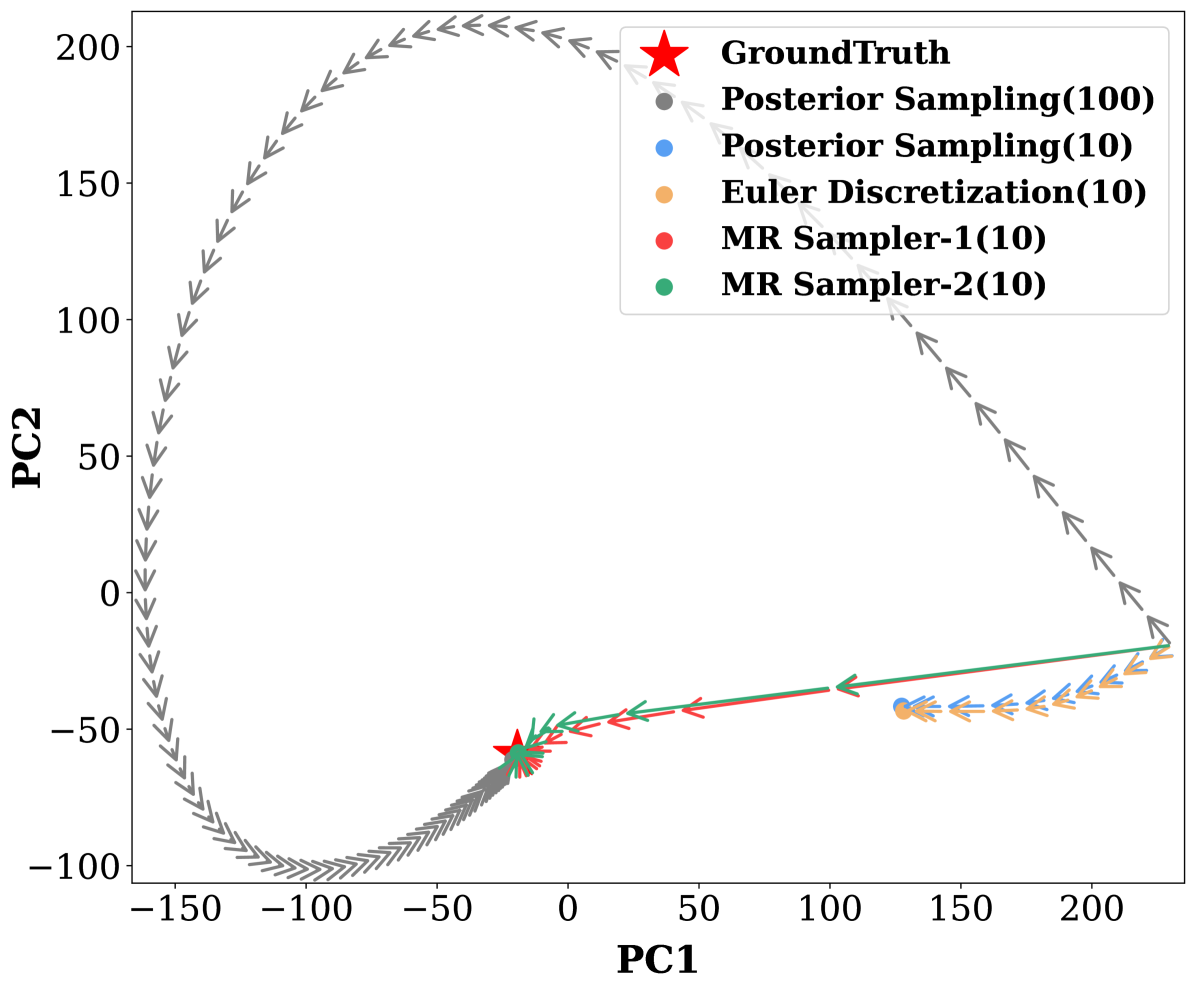
🔼 This figure visualizes the sampling trajectories of different sampling methods in a 2D space using PCA, starting from a random point and converging towards the ground truth. The figure helps illustrate the efficiency of the proposed MR Sampler by comparing its direct trajectory to the longer, less efficient paths of previous methods.
read the caption
(b) Trajectory.

🔼 Figure 3 visualizes the sampling process of different diffusion models. Panel (a) presents a comparison of the sampling results from various methods, including posterior sampling, Euler discretization, and the proposed MR Sampler (with order 1 and 2), applied to a motion-blurred image. The number of function evaluations (NFEs) used in each method is indicated in parentheses. Panel (b) shows the sampling trajectories in a two-dimensional principal component analysis (PCA) space for each of the methods. The trajectories demonstrate that the proposed MR Sampler methods reach the true sample (x0) more efficiently (with fewer steps) than the other methods that take more indirect paths.
read the caption
Figure 3: Sampling trajectories. In (a), we compare our method (with order 1 and order 2) and previous sampling methods (i.e., posterior sampling and Euler discretization) on a motion blurry image. The numbers in parentheses indicate the NFE. In (b), we illustrate trajectories of each sampling method. Previous methods need to take many unnecessary paths to converge. With few NFEs, they fail to reach the ground truth (i.e., the location of 𝒙0subscript𝒙0\bm{x}_{0}bold_italic_x start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT). Our methods follow a more direct trajectory.

NFE	Parameterization	LPIPS↓	FID↓	PSNR↑	SSIM↑
50	Noise Prediction	0.0606	27.28	28.89	0.8615
50	Data Prediction	0.0620	27.65	28.85	0.8602
20	Noise Prediction	0.1429	47.31	27.68	0.7954
20	Data Prediction	0.0635	27.79	28.60	0.8559
10	Noise Prediction	1.376	402.3	6.623	0.0114
10	Data Prediction	0.0678	29.54	28.09	0.8483
5	Noise Prediction	1.416	447.0	5.755	0.0051
5	Data Prediction	0.0637	26.92	28.82	0.8685

NFE	Solver Type	LPIPS↓	FID↓	PSNR↑	SSIM↑
50	ODE	0.0499	22.91	28.49	0.8921
50	SDE	0.0402	19.09	29.15	0.9046
20	ODE	0.0475	21.35	28.51	0.8940
20	SDE	0.0408	19.13	28.98	0.9032
10	ODE	0.0417	19.44	28.94	0.9048
10	SDE	0.0437	19.29	28.48	0.8996
5	ODE	0.0526	27.44	31.02	0.9335
5	SDE	0.0529	24.02	28.35	0.8930

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

ODE/SDE Solvers#

MRS Sampler#

Data Prediction#

Numerical Stability#

Future Work#

More visual insights#

Full paper#