TL;DR#
Current process verification methods for large language models (LLMs) often struggle with complex reasoning tasks and noisy data. Existing systems either make simplistic binary decisions or are computationally expensive, leading to unreliable evaluations and hindering the development of more robust AI systems. This research highlights a critical need for more sophisticated and efficient verification techniques.
The paper introduces Dyve, a novel dynamic process verifier that employs a dual-system approach mimicking human cognitive processes: ‘fast’ (immediate token-level confirmation) and ‘slow’ (comprehensive analysis) thinking. Dyve leverages Monte Carlo estimation and a novel step-wise consensus-filtered supervision to improve accuracy. Experiments show that Dyve significantly outperforms other methods on various benchmarks, particularly excelling on more complex reasoning tasks, and demonstrating the effectiveness of its dual-system approach in achieving high accuracy with reasonable computational efficiency.
Key Takeaways#
Why does it matter?#
This paper is important because it presents Dyve, a novel dynamic process verifier that significantly improves the accuracy of reasoning error detection in large language models. Its adaptive approach, combining fast and slow thinking, addresses the limitations of existing methods that rely on simplistic binary classifications or are computationally expensive. This work opens up new avenues for research in process verification and reliable LLM evaluation, impacting various AI applications that rely on reasoning accuracy.
Visual Insights#

🔼 Figure 1 illustrates the limitations of existing approaches to process verification in LLMs and introduces Dyve as a superior alternative. It compares five methods: 1. LLM Self-Reflection: Shows the unreliability of LLMs relying solely on their internal reflection mechanisms for identifying errors. 2. Binary Verification: Highlights the lack of depth in simple yes/no verification systems, which fail to capture the nuances of complex reasoning processes. 3. Chain-of-Thought (CoT) Verification: Demonstrates that while deeper analysis offered by CoT methods improves accuracy, it comes at a higher computational cost. 4. GenRM with CoT: Illustrates that generative models (GenRMs) using CoT may combine generation and verification but lack the step-wise assessment crucial for precise error identification. 5. Dyve: Introduces Dyve, the proposed model, which dynamically combines the speed of System 1 (fast, intuitive verification) and the thoroughness of System 2 (deeper analysis) verification to achieve optimal performance.
read the caption
Figure 1: (1) LLM self-reflection is unreliable (2) Binary verification lacks depth, (3) Chain-of-Thought (CoT) verification is deeper but more expensive, (4) GenRM with CoT combines generation and verification without step-wise assessment, (5) Dyve, our proposed framework that dynamically combines fast System 1 and deep System 2 verification.
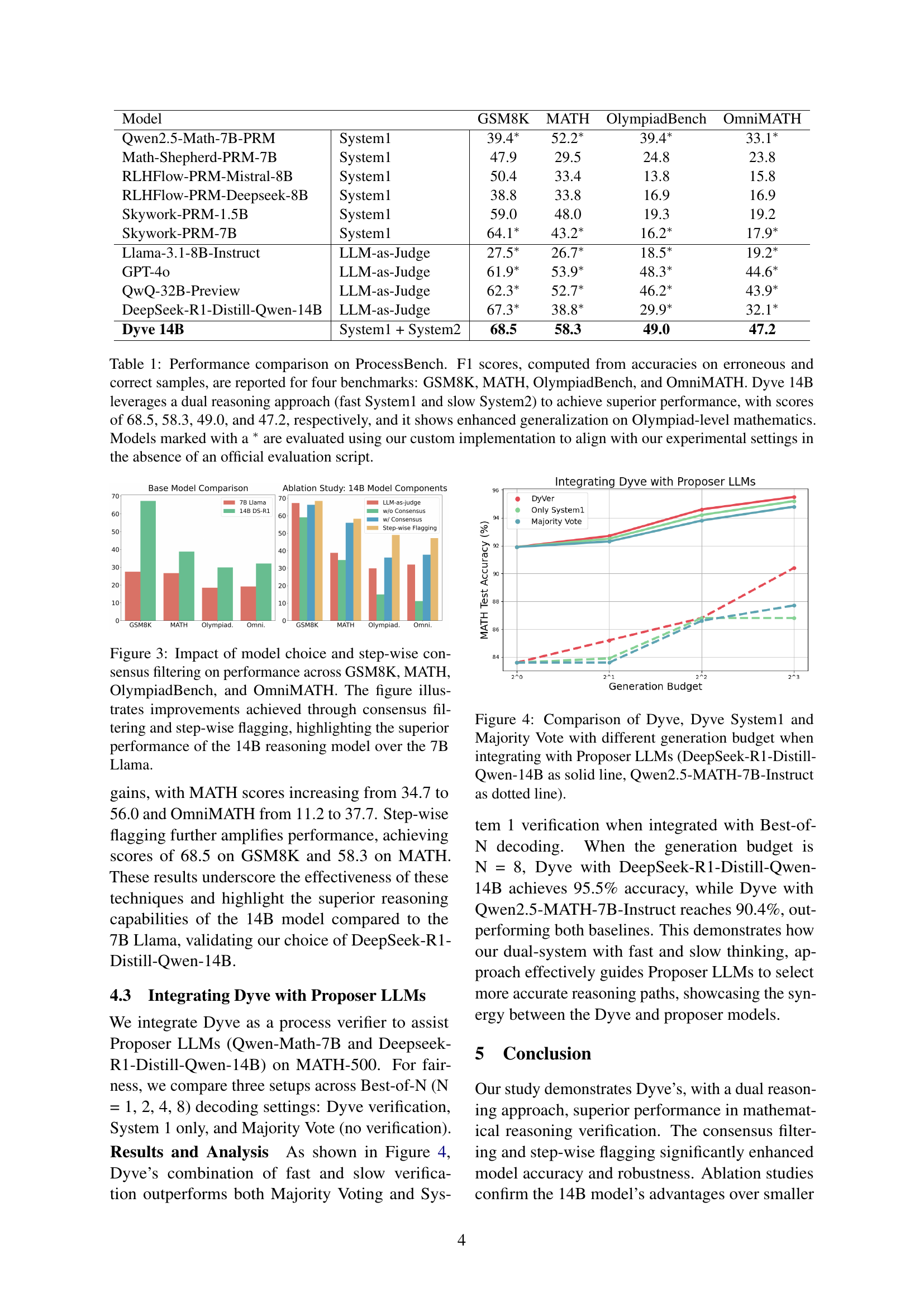
| Model | GSM8K | MATH | OlympiadBench | OmniMATH | |
|---|---|---|---|---|---|
| Qwen2.5-Math-7B-PRM | System1 | 39.4∗ | 52.2∗ | 39.4∗ | 33.1∗ |
| Math-Shepherd-PRM-7B | System1 | 47.9 | 29.5 | 24.8 | 23.8 |
| RLHFlow-PRM-Mistral-8B | System1 | 50.4 | 33.4 | 13.8 | 15.8 |
| RLHFlow-PRM-Deepseek-8B | System1 | 38.8 | 33.8 | 16.9 | 16.9 |
| Skywork-PRM-1.5B | System1 | 59.0 | 48.0 | 19.3 | 19.2 |
| Skywork-PRM-7B | System1 | 64.1∗ | 43.2∗ | 16.2∗ | 17.9∗ |
| Llama-3.1-8B-Instruct | LLM-as-Judge | 27.5∗ | 26.7∗ | 18.5∗ | 19.2∗ |
| GPT-4o | LLM-as-Judge | 61.9∗ | 53.9∗ | 48.3∗ | 44.6∗ |
| QwQ-32B-Preview | LLM-as-Judge | 62.3∗ | 52.7∗ | 46.2∗ | 43.9∗ |
| DeepSeek-R1-Distill-Qwen-14B | LLM-as-Judge | 67.3∗ | 38.8∗ | 29.9∗ | 32.1∗ |
| Dyve 14B | System1 + System2 | 68.5 | 58.3 | 49.0 | 47.2 |
🔼 This table presents a performance comparison of different models on the ProcessBench benchmark, which evaluates the ability of models to detect errors in multi-step mathematical reasoning. The benchmark uses four datasets: GSM8K, MATH, OlympiadBench, and OmniMATH, each with increasing difficulty. The table reports F1 scores for each model, calculated from the harmonic mean of precision and recall on erroneous and correct samples. Dyve 14B, which uses a combined fast (System 1) and slow (System 2) reasoning approach, achieves superior performance across all datasets, especially demonstrating strong generalization to the most challenging Olympiad-level mathematics problems. Note that some models marked with an asterisk (*) were evaluated using a custom implementation due to a lack of official evaluation scripts for those models, ensuring fair comparison with the other models.
read the caption
Table 1: Performance comparison on ProcessBench. F1 scores, computed from accuracies on erroneous and correct samples, are reported for four benchmarks: GSM8K, MATH, OlympiadBench, and OmniMATH. Dyve 14B leverages a dual reasoning approach (fast System1 and slow System2) to achieve superior performance, with scores of 68.5, 58.3, 49.0, and 47.2, respectively, and it shows enhanced generalization on Olympiad-level mathematics. Models marked with a ∗ are evaluated using our custom implementation to align with our experimental settings in the absence of an official evaluation script.
In-depth insights#
Dyve’s Dual System#
Dyve’s core innovation lies in its dual-system approach, mirroring Kahneman’s Systems 1 and 2 thinking. System 1 provides rapid, intuitive token-level verification for straightforward steps, enhancing efficiency. System 2, activated for complex steps, engages in a more thorough, deliberative analysis. This adaptive strategy is crucial because simplistic binary yes/no verification methods fail to capture the nuances of complex reasoning processes. The integration of Monte Carlo estimation, LLM-as-a-judge, and specialized reasoning models generates high-quality training data, overcoming limitations of noisy datasets. Dyve’s dynamic shift between these two systems optimizes both speed and accuracy, representing a significant advancement in dynamic process verification. The system’s effectiveness stems from its ability to avoid both the oversimplification of System 1 and the inefficiency of a solely System 2 approach.
Adaptive Verification#
Adaptive verification in dynamic process verification systems is crucial for efficient and accurate error detection. The core idea is to tailor the verification process to the complexity of each step in a reasoning trace. Instead of applying a uniform verification strategy, an adaptive system would use a lightweight, fast approach for straightforward steps and a more thorough, computationally expensive method for complex or ambiguous steps. This approach mirrors human cognitive processes, where we use intuition for simple tasks and deliberate reasoning for challenging ones. This system is especially valuable for large language models (LLMs), which are prone to both simple mistakes and subtle, systemic reasoning errors. The adaptive nature of the verification enhances efficiency by avoiding the unnecessary cost of in-depth analysis for simple steps, allowing for faster overall processing of longer reasoning traces. A key challenge in implementing this lies in reliably identifying steps that require different levels of scrutiny. This requires a robust method for classifying step complexity, perhaps using a combination of heuristics and machine learning techniques trained on labeled data to distinguish straightforward and complex reasoning steps. The success of adaptive verification hinges on striking a balance between accuracy and efficiency. An ideal system would dynamically adjust its verification strategy based on real-time assessment of step complexity, leading to more accurate error detection with optimal resource utilization.
LLM-as-a-Judge#
The concept of “LLM-as-a-Judge” presents a novel approach to enhancing the accuracy of process verification in large language models (LLMs). It leverages the capabilities of a powerful LLM to evaluate the quality and correctness of the process, offering a more sophisticated level of analysis than traditional binary classification methods. Instead of simply accepting or rejecting a single step, the LLM acts as an arbiter, meticulously examining the reasoning process for potential flaws, inconsistencies, or leaps in logic. This approach is particularly beneficial for handling complex problems or incomplete reasoning traces where simpler methods might fail. By incorporating an LLM’s ability to reason and understand context, the judgment becomes more nuanced, potentially leading to more accurate identification of errors. This system helps address the challenge of noisy or unreliable labels in training data; by filtering out questionable outputs, it allows the training process to focus on high-quality examples. While this technique enhances verification precision, its computational cost needs careful consideration. The reliance on a second, potentially expensive LLM introduces an overhead that must be balanced against the gains in accuracy. Further research should explore methods for optimizing this efficiency, such as using smaller, more specialized LLMs for the judging task, or focusing on identifying specific error types to streamline the evaluation process. The effectiveness of LLM-as-a-Judge strongly depends on the quality of the underlying LLM; a poorly trained or biased LLM might produce inaccurate judgments. Therefore, selection and training of the judging LLM are critical components to be addressed in future work.
ProcessBench Results#
The ProcessBench results section would be crucial in evaluating the effectiveness of Dyve. It would likely present F1 scores, a balanced measure of precision and recall, across various subsets of ProcessBench, such as GSM8k, MATH, OlympiadBench, and OmniMATH, reflecting different difficulty levels and problem types. High F1 scores across all subsets would strongly indicate Dyve’s robustness and generalizability. A comparison against other state-of-the-art process verifiers (PRMs) would be essential, demonstrating Dyve’s superior performance. The analysis should delve into whether Dyve excels more in specific subsets, potentially revealing strengths and weaknesses. Furthermore, inference speed comparisons are critical; while accuracy is paramount, Dyve’s efficiency (latency per sample) must be competitive for practical applications. Finally, an in-depth exploration of error analysis—identifying the types of errors where Dyve excels or falters—would offer key insights into its capabilities and limitations, paving the way for future improvements.
Future Enhancements#
Future enhancements for Dyve should prioritize improving the robustness of the step-wise consensus filtering process by exploring more sophisticated LLM-as-a-judge models and potentially incorporating human-in-the-loop validation for ambiguous cases. Expanding the scope of supported reasoning tasks beyond mathematical problems is crucial to demonstrate broader applicability. This might involve developing specialized modules for different reasoning domains or adopting a more flexible, domain-agnostic architecture. Further research should investigate the integration of Dyve with other AI systems, such as planning or knowledge representation modules, enabling more comprehensive AI verification pipelines. Finally, developing more efficient inference strategies is needed to address the computational overhead, perhaps through model compression or optimized inference techniques, to make Dyve suitable for real-world applications.
More visual insights#
More on figures

🔼 This figure presents a bar chart comparing the inference speed of three different models on the ProcessBench dataset: System-1, Dyve, and DeepSeek-R1-14B. The y-axis represents the time per sample in seconds, and the x-axis shows the four subsets of ProcessBench (GSM8K, MATH, Olympiad, Omni). The chart visually demonstrates the relative efficiency of each model across different problem complexities, allowing for a comparison of their computational performance. It shows that System-1 is the fastest, Dyve is moderately fast, balancing speed and performance, and DeepSeek-R1-14B is the slowest.
read the caption
Figure 2: Inference speed comparison on ProcesBench, time per sample in seconds, for System-1, Dyve, and DeepSeek-R1-14B.

🔼 Figure 3 presents a detailed analysis of how model selection and the step-wise consensus filtering technique impact the performance of a process verification model across four benchmark datasets: GSM8K, MATH, OlympiadBench, and OmniMATH. The bar charts compare the accuracy of different models (a 7B parameter Llama model and a 14B parameter DeepSeek model) with and without consensus filtering and step-wise flagging. The results clearly demonstrate that employing consensus filtering and step-wise flagging significantly improves accuracy, particularly with the larger, 14B parameter model. This showcases the effectiveness of these techniques in enhancing the model’s ability to accurately identify process errors.
read the caption
Figure 3: Impact of model choice and step-wise consensus filtering on performance across GSM8K, MATH, OlympiadBench, and OmniMATH. The figure illustrates improvements achieved through consensus filtering and step-wise flagging, highlighting the superior performance of the 14B reasoning model over the 7B Llama.

🔼 This figure compares the performance of three different methods for mathematical problem solving when integrated with two different proposer LLMs. The methods compared are: Dyve (which combines fast and slow thinking), Dyve System 1 (fast thinking only), and Majority Vote (a simpler method). The two proposer LLMs used are DeepSeek-R1-Distill-Qwen-14B (solid line) and Qwen2.5-MATH-7B-Instruct (dotted line). The x-axis represents the generation budget (number of attempts to generate a solution), and the y-axis shows the accuracy achieved. The figure demonstrates how Dyve’s adaptive approach improves accuracy compared to the other methods, especially with larger generation budgets.
read the caption
Figure 4: Comparison of Dyve, Dyve System1 and Majority Vote with different generation budget when integrating with Proposer LLMs (DeepSeek-R1-Distill-Qwen-14B as solid line, Qwen2.5-MATH-7B-Instruct as dotted line).
Full paper#