TL;DR#
Fine-tuning diffusion models to match user preferences is challenging. Existing methods either focus on single timesteps (neglecting trajectory-level alignment) or incur high computational costs. This paper introduces Diffusion-Sharpening, a new fine-tuning approach that directly optimizes the entire sampling trajectory during training. This is achieved using a path integral framework that leverages reward feedback and amortizes inference costs.
Diffusion-Sharpening boasts superior training efficiency (faster convergence) and best inference efficiency (no extra NFEs). Experiments across various metrics (text alignment, compositional abilities, user preferences) demonstrate that Diffusion-Sharpening surpasses existing RL-based fine-tuning and sampling trajectory optimization methods. The method’s efficiency and scalability make it highly suitable for fine-tuning large diffusion models.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel and efficient fine-tuning approach for diffusion models, addressing the limitations of existing methods in terms of training efficiency and inference cost. Its impact lies in improving the alignment of generated outputs with user preferences, enabling more precise control over the generation process and opening new avenues for research in generative AI. The proposed method’s scalability and efficiency make it highly relevant to current research trends focusing on improving the performance of large generative models.
Visual Insights#

🔼 Figure 1 illustrates three distinct approaches to optimizing diffusion models using reward signals. (i) Diffusion Reinforcement Learning focuses on optimizing a single timestep using reinforcement learning techniques, ignoring the trajectory leading up to that step. (ii) Diffusion Sampling Trajectory Optimization extends optimization to the entire sampling trajectory, but this method involves high computational costs. (iii) Diffusion Sharpening, the proposed method, optimizes the sampling trajectory in a more efficient manner using a path integral framework that leverages reward feedback during training to select optimal trajectories and amortizes inference costs.
read the caption
Figure 1: Comparison of Three Diffusion-Based Methods for Reward-Driven Optimization: (i) Diffusion Reinforcement Learning, (ii) Diffusion Sampling Trajectory Optimization, and (iii) Diffusion Sharpening.
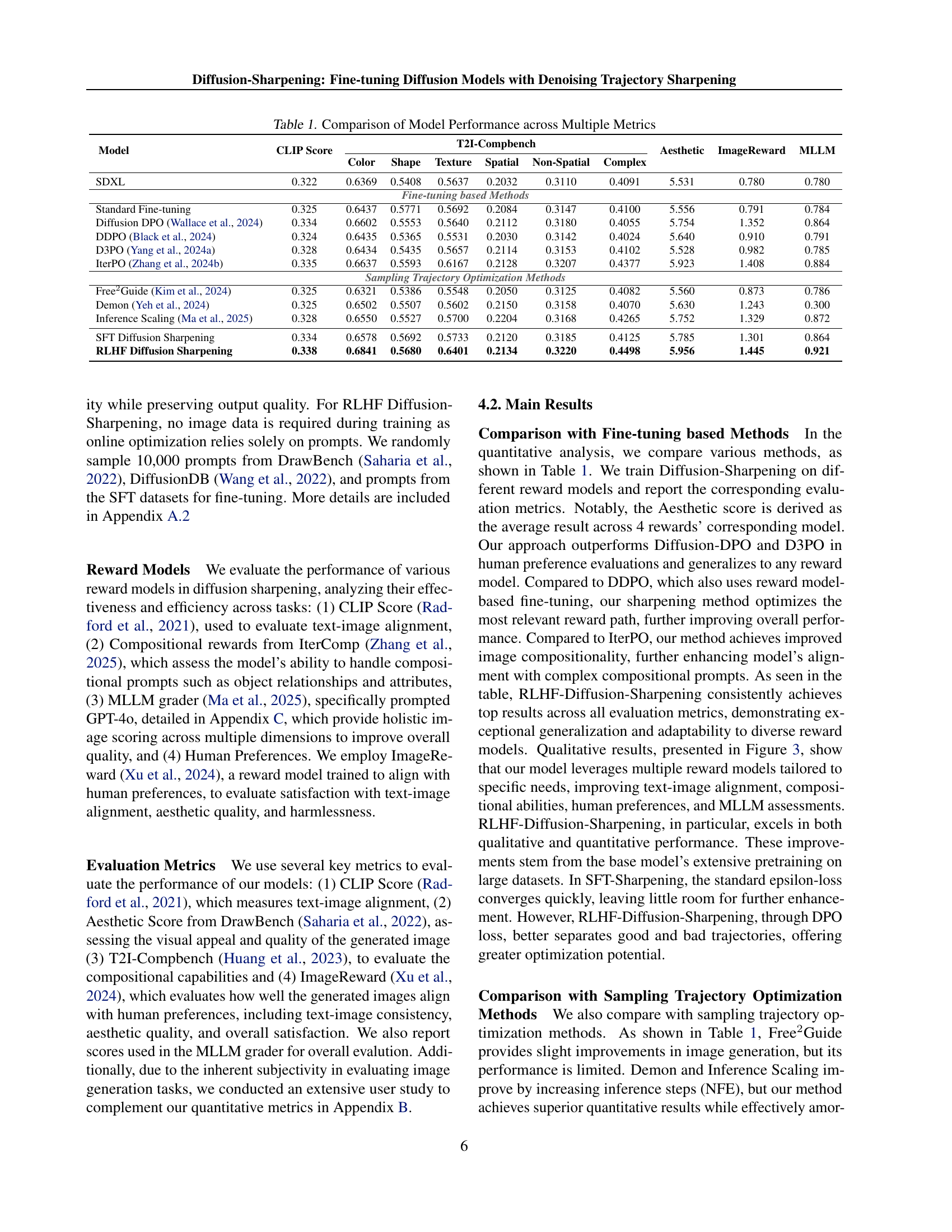
| Model | CLIP Score | T2I-Compbench | Aesthetic | ImageReward | MLLM | |||||
| Color | Shape | Texture | Spatial | Non-Spatial | Complex | |||||
| SDXL | 0.322 | 0.6369 | 0.5408 | 0.5637 | 0.2032 | 0.3110 | 0.4091 | 5.531 | 0.780 | 0.780 |
| Fine-tuning based Methods | ||||||||||
| Standard Fine-tuning | 0.325 | 0.6437 | 0.5771 | 0.5692 | 0.2084 | 0.3147 | 0.4100 | 5.556 | 0.791 | 0.784 |
| Diffusion DPO (Wallace et al., 2024) | 0.334 | 0.6602 | 0.5553 | 0.5640 | 0.2112 | 0.3180 | 0.4055 | 5.754 | 1.352 | 0.864 |
| DDPO (Black et al., 2024) | 0.324 | 0.6435 | 0.5365 | 0.5531 | 0.2030 | 0.3142 | 0.4024 | 5.640 | 0.910 | 0.791 |
| D3PO (Yang et al., 2024a) | 0.328 | 0.6434 | 0.5435 | 0.5657 | 0.2114 | 0.3153 | 0.4102 | 5.528 | 0.982 | 0.785 |
| IterPO (Zhang et al., 2024b) | 0.335 | 0.6637 | 0.5593 | 0.6167 | 0.2128 | 0.3207 | 0.4377 | 5.923 | 1.408 | 0.884 |
| Sampling Trajectory Optimization Methods | ||||||||||
| Free2Guide (Kim et al., 2024) | 0.325 | 0.6321 | 0.5386 | 0.5548 | 0.2050 | 0.3125 | 0.4082 | 5.560 | 0.873 | 0.786 |
| Demon (Yeh et al., 2024) | 0.325 | 0.6502 | 0.5507 | 0.5602 | 0.2150 | 0.3158 | 0.4070 | 5.630 | 1.243 | 0.300 |
| Inference Scaling (Ma et al., 2025) | 0.328 | 0.6550 | 0.5527 | 0.5700 | 0.2204 | 0.3168 | 0.4265 | 5.752 | 1.329 | 0.872 |
| SFT Diffusion Sharpening | 0.334 | 0.6578 | 0.5692 | 0.5733 | 0.2120 | 0.3185 | 0.4125 | 5.785 | 1.301 | 0.864 |
| RLHF Diffusion Sharpening | 0.338 | 0.6841 | 0.5680 | 0.6401 | 0.2134 | 0.3220 | 0.4498 | 5.956 | 1.445 | 0.921 |
🔼 Table 1 presents a comprehensive comparison of various diffusion models’ performance across multiple evaluation metrics. It compares standard fine-tuning methods, other reward-based fine-tuning methods, sampling trajectory optimization methods, and the proposed Diffusion-Sharpening approach (both SFT and RLHF versions). The metrics used for comparison include CLIP Score, which assesses image-text alignment; aesthetic scores, reflecting overall visual quality; T2I-Compbench scores, evaluating compositional capabilities; and MLLM (Multimodal Large Language Model) grader scores, providing a holistic assessment across several dimensions. The results showcase the strengths and weaknesses of each method in terms of training efficiency, inference efficiency, image quality, and alignment with user preferences.
read the caption
Table 1: Comparison of Model Performance across Multiple Metrics
In-depth insights#
Trajectory Optimization#
The concept of trajectory optimization in the context of diffusion models is crucial for enhancing the quality and efficiency of generated outputs. Existing methods often focus on single timesteps, neglecting the overall coherence and alignment across the entire denoising process. This limitation leads to suboptimal results and high computational costs. Diffusion-Sharpening addresses this by directly optimizing the sampling trajectories during training, enabling real-time adjustments during diffusion and leading to more consistent, high-quality outputs. This approach leverages path integration to select optimal trajectories, providing feedback to guide the model toward improvements. A key advantage is the amortization of inference costs, meaning the model learns efficient trajectories, avoiding the computationally expensive searches characteristic of other trajectory optimization approaches. By integrating reward feedback into the trajectory optimization process, Diffusion-Sharpening achieves superior alignment with user preferences or predefined criteria. This allows it to effectively fine-tune diffusion models for tasks requiring fine-grained or domain-specific control.
RLHF vs. SFT#
The comparison of RLHF (Reinforcement Learning from Human Feedback) and SFT (Supervised Fine-Tuning) in the context of fine-tuning diffusion models is crucial. SFT uses a pre-existing dataset of image-text pairs to directly train or fine-tune the model, leading to relatively fast and efficient training. However, SFT’s performance heavily relies on the quality and representativeness of the training data. Biases in the dataset will directly translate into biases in the generated images. RLHF, on the other hand, employs a reward model that assesses generated images based on human preferences, allowing for more flexible and nuanced control over the generated output. RLHF is iterative and computationally expensive, requiring multiple stages of training and evaluation, including a training stage to optimize the reward model itself. Despite the higher computational cost, RLHF offers the potential to achieve superior alignment with human preferences and to mitigate biases present in pre-existing datasets. The optimal choice between RLHF and SFT depends on the specific application, dataset availability, and computational resources. In scenarios where high-quality, human-aligned results are paramount and computational cost is less of a concern, RLHF is preferable. Conversely, when computational resources are limited or a large, high-quality dataset is available, SFT might be a more viable option.
Reward Model Impact#
The choice of reward model significantly impacts the performance of Diffusion-Sharpening. Different reward models capture different aspects of image quality and alignment with user preferences. Using only CLIP scores, for example, might optimize for textual similarity but neglect other crucial factors like aesthetic appeal or compositional coherence. In contrast, incorporating human feedback or more sophisticated metrics like MLLM evaluations provides a more holistic assessment leading to substantial improvements in overall generation quality. The paper highlights the flexibility of Diffusion-Sharpening by demonstrating its adaptability to diverse reward models, enabling researchers to tailor the fine-tuning process to specific applications and evaluation criteria. The results underscore the importance of selecting or designing reward models that comprehensively capture the desired qualities, thereby maximizing the effectiveness of the Diffusion-Sharpening framework and improving the generated images’ fidelity, alignment, and overall user satisfaction.
Efficiency Analysis#
An efficiency analysis of the Diffusion-Sharpening model would ideally delve into both training efficiency and inference efficiency. For training, the key metric would be the convergence rate, comparing the number of training steps needed to reach a satisfactory performance level against other fine-tuning methods. Faster convergence translates to reduced computational costs and time. The analysis should also investigate the impact of hyperparameters such as the number of samples and trajectory steps on training efficiency. Regarding inference, the critical factor is the number of forward diffusion steps (NFEs) required for generating a sample. Diffusion-Sharpening aims to improve inference efficiency by optimizing sampling trajectories during training, reducing NFEs at inference time. A comparison with baselines like Demon and Inference Scaling, which directly optimize the sampling trajectory during inference but at high computational costs, would highlight the benefits of Diffusion-Sharpening’s approach. The analysis should quantify improvements in terms of inference time and NFE reduction. Ultimately, a comprehensive efficiency analysis would demonstrate the scalability and practicality of the Diffusion-Sharpening method by showing its superior performance in both training and inference compared to state-of-the-art approaches while maintaining high generative quality.
Future Directions#
Future research could explore extending Diffusion-Sharpening to other generative models, such as those based on GANs or VAEs, to determine the broad applicability of trajectory optimization. Investigating alternative reward models and their impact on generated outputs is crucial. This includes exploring methods beyond CLIP and developing reward functions sensitive to nuanced aspects of quality, such as composition and realism. A key area is improving the scalability of Diffusion-Sharpening for high-resolution images and complex generation tasks. This requires addressing computational challenges related to path integration and reward aggregation across many trajectories. Finally, in-depth investigations into the theoretical properties of Diffusion-Sharpening, including convergence rates and generalization capabilities are needed. This would enhance our understanding and lead to more efficient algorithms.
More visual insights#
More on figures

🔼 This figure illustrates the Diffusion Sharpening framework, showcasing its training, inference, and reward model selection processes. Panel (i) details the training phase, emphasizing trajectory-level optimization and the use of sharpening loss to refine denoising trajectories. Panel (ii) depicts the inference stage, demonstrating how the sharpened denoising trajectory leads to improved generative output quality. Finally, Panel (iii) highlights the flexibility of the framework by demonstrating the capability to integrate diverse reward models such as CLIP scores, compositional metrics from MLLMs, and human preference models, offering a highly adaptable and configurable fine-tuning method.
read the caption
Figure 2: Overview of Our Diffusion Sharpening Framework: (i) Training, (ii) Inference, and (iii) Reward Model Selection

🔼 Figure 3 presents a qualitative comparison of image generation results obtained using different diffusion sharpening methods and reward models. The figure is divided into four sections, each corresponding to a specific reward model: CLIP Score, Compositional Reward, MLLM, and Human Preferences. Within each section, multiple images generated by three different methods are displayed: a baseline model and the two proposed Diffusion Sharpening approaches (SFT and RLHF). This allows for a visual comparison of the impact of each method on the generated images under different reward structures. The purpose is to demonstrate the effectiveness of the SFT and RLHF Diffusion Sharpening methods in improving the quality and alignment of generated images according to diverse evaluation criteria.
read the caption
Figure 3: Qualitative results comparing Diffusion Sharpening methods using different reward models. The images show the generated results with CLIP Score, Compositional Reward, MLLM, and Human Preferences as reward models, showcasing the effectiveness of SFT Diffusion Sharpening and RLHF Diffusion Sharpening in diffusion finetuning.
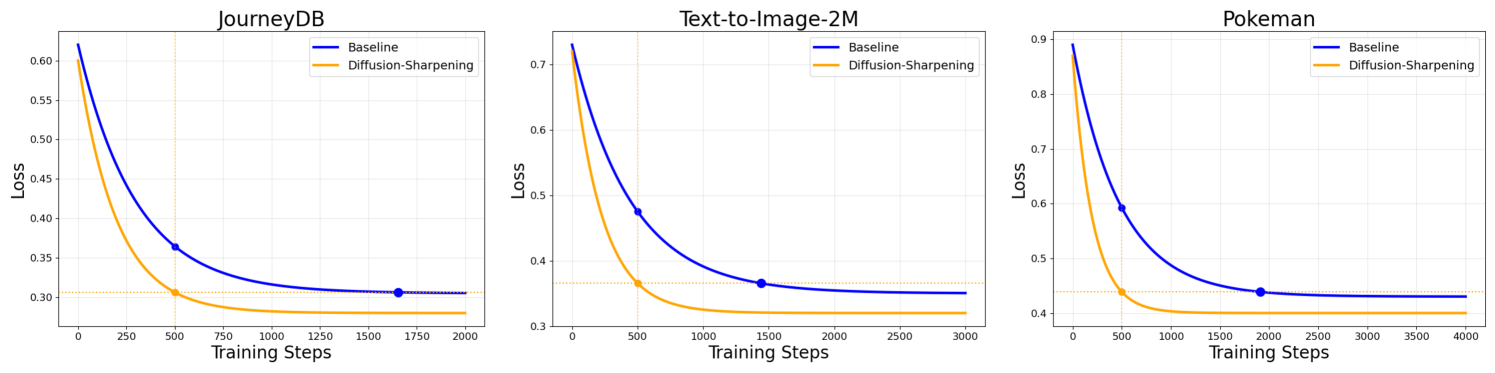
🔼 This figure displays the training loss curves for fine-tuning the SDXL model across three different datasets: JourneyDB, Text-to-Image-2M, and Pokemon. Each curve represents the loss for a different fine-tuning method, comparing the standard baseline method against the SFT (Supervised Fine-Tuning) Diffusion-Sharpening approach. The x-axis shows the number of training steps, and the y-axis shows the training loss. The plots illustrate how the loss changes over the course of training for each dataset and method, demonstrating the relative convergence speeds and final loss values.
read the caption
Figure 4: SDXL Finetuning Loss across Difference Datasets. Here ”Diffusion-Sharpening” represents SFT Diffusion-Sharpening specifically.

🔼 This figure demonstrates the inference efficiency of the proposed Diffusion Sharpening method compared to other sampling trajectory optimization methods. It shows how inference time (measured in number of function evaluations, or NFEs) impacts the CLIP score, a measure of image-text alignment quality. Diffusion Sharpening achieves superior performance with significantly fewer NFEs compared to the alternatives like Demon and Inference Scaling, highlighting its computational efficiency.
read the caption
Figure 5: Inference Performance of Diffusion Sharpening.

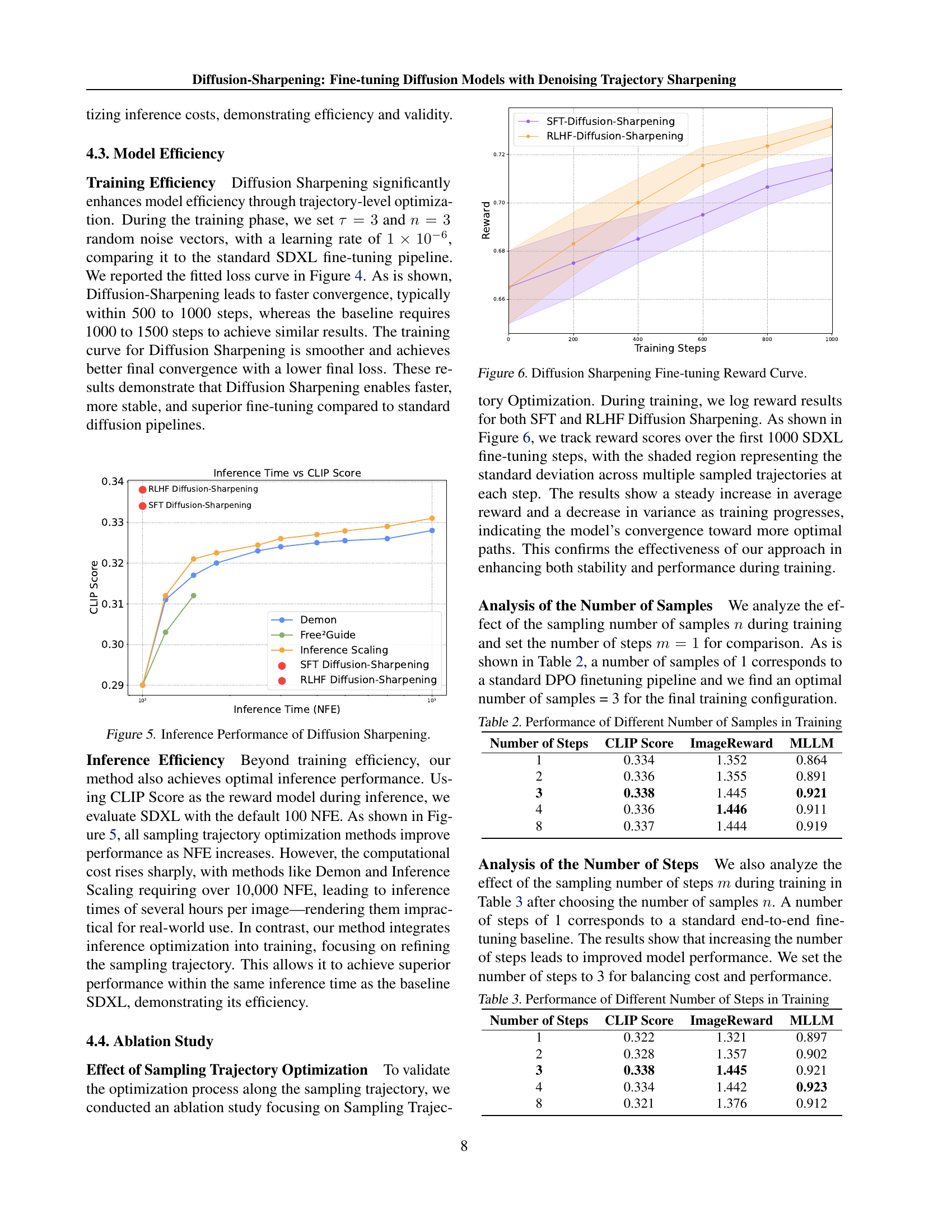
🔼 This figure shows the reward curves during the fine-tuning process for both SFT and RLHF Diffusion Sharpening methods. The x-axis represents the number of training steps, and the y-axis shows the average reward. The shaded area around the curves represents the standard deviation across multiple sampled trajectories at each step. The plot visually demonstrates the convergence of both methods towards higher rewards as training progresses, indicating that the models are learning to generate more optimal trajectories. The curves also show that the RLHF method reaches higher rewards faster than the SFT method.
read the caption
Figure 6: Diffusion Sharpening Fine-tuning Reward Curve.

🔼 This figure presents the results of a user study comparing the performance of Diffusion-Sharpening with other methods. Users were shown pairs of images generated by different models and asked to select their preferred image. The results are displayed as a bar chart showing the percentage of times each model was chosen as preferred. This allows for a direct comparison of the visual quality and user preference between Diffusion-Sharpening and other fine-tuning or optimization methods.
read the caption
Figure 7: User Study about Comparision with Other Methods

🔼 This figure details the instructions given to a large language model (LLM) to evaluate images generated by a text-to-image model. The LLM is instructed to provide a score (0-10) and justification for five aspects of each image: accuracy to prompt, creativity and originality, visual quality and realism, consistency and cohesion, and emotional or thematic resonance. The LLM should also provide a final weighted overall score for the image.
read the caption
Figure 8: The detailed prompt for evaluation with the MMLLM Grader.

🔼 This figure displays a diverse set of images generated using the SFT Diffusion-Sharpening method. Each image showcases the method’s ability to generate high-quality and detailed outputs across a variety of styles, themes, and subject matters. The images demonstrate a balance between realism and creativity, and suggest the model’s skill in achieving high levels of compositional coherence and artistic proficiency. The diverse subjects further demonstrate SFT Diffusion-Sharpening’s capabilities for general image generation, rather than specialization in a specific domain or aesthetic.
read the caption
Figure 9: More Qualitative Results for SFT Diffusion-Sharpening.
More on tables
| Number of Steps | CLIP Score | ImageReward | MLLM |
| 1 | 0.334 | 1.352 | 0.864 |
| 2 | 0.336 | 1.355 | 0.891 |
| 3 | 0.338 | 1.445 | 0.921 |
| 4 | 0.336 | 1.446 | 0.911 |
| 8 | 0.337 | 1.444 | 0.919 |
🔼 This table presents the results of an ablation study on the effect of varying the number of samples used during training of the Diffusion Sharpening model. It shows how different numbers of samples (1, 2, 3, 4, 8) affect the performance metrics of CLIP score, ImageReward, and MLLM, which evaluate different aspects of image generation quality. The purpose of this experiment is to determine the optimal number of samples that balances performance and computational cost.
read the caption
Table 2: Performance of Different Number of Samples in Training
| Number of Steps | CLIP Score | ImageReward | MLLM |
| 1 | 0.322 | 1.321 | 0.897 |
| 2 | 0.328 | 1.357 | 0.902 |
| 3 | 0.338 | 1.445 | 0.921 |
| 4 | 0.334 | 1.442 | 0.923 |
| 8 | 0.321 | 1.376 | 0.912 |
🔼 This table presents the results of an ablation study on the effect of varying the number of steps (m) in the training process of the Diffusion-Sharpening model. It shows how the model’s performance, measured by CLIP Score, ImageReward, and MLLM scores, changes as the number of steps increases from 1 to 8. A value of 1 step represents standard end-to-end fine-tuning, while higher numbers of steps incorporate more trajectory-level optimization. The table helps to determine the optimal number of steps for balancing performance and computational cost.
read the caption
Table 3: Performance of Different Number of Steps in Training
Full paper#