Learning Getting-Up Policies for Real-World Humanoid Robots

2502.12152

Xialin He et el.

🤗 2025-02-18

TL;DR
#

Humanoid robots’ real-world deployment is hindered by the lack of robust fall recovery mechanisms. Hand-designing controllers is difficult due to the robot’s varied post-fall configurations and unpredictable terrains. Previous locomotion learning methods are inadequate due to the non-periodic and contact-rich nature of the getting-up task. This poses significant challenges for reward design and controller optimization.

To address these issues, the paper introduces HUMANUP, a novel two-stage reinforcement learning framework. Stage I focuses on discovering effective getting-up trajectories, while Stage II refines these trajectories for real-world deployment by optimizing smoothness and robustness. The framework incorporates a curriculum for learning, starting with simpler settings and gradually increasing complexity. The results demonstrate that the learned policies enable a real-world humanoid robot to successfully get up from various lying postures and on diverse terrains, significantly exceeding the performance of existing hand-engineered controllers.

Key Takeaways
#

Why does it matter?
#

This paper is crucial because fall recovery is a critical unsolved problem for humanoid robots; enabling robots to autonomously recover from falls significantly advances their real-world applicability and safety. The research directly addresses this need, offering a novel learning-based approach that exhibits robustness and generalizability. This opens avenues for developing more resilient and adaptable robots that can operate reliably in complex and unpredictable environments, improving their utility in various applications like search and rescue, disaster relief, and industrial settings. Furthermore, the two-stage training method and the detailed analysis of various factors affecting recovery provide valuable insights for future research in humanoid robotics control and learning.

Visual Insights
#

🔼 This figure showcases the effectiveness of the HumanUP framework. It demonstrates the ability of a Unitree G1 humanoid robot to recover from various lying positions (both on its back and stomach) on different terrains. HumanUP uses a two-stage training approach, resulting in robust and smooth getting-up motions. The image displays the robot successfully getting up from different lying positions on diverse surfaces like grass, slopes and tiles.
read the caption
Figure 1: HumanUP provides a simple and general two-stage training method for humanoid getting-up tasks, which can be directly deployed on Unitree G1 humanoid robots [70]. Our policies showcase robust and smooth behavior that can get up from diverse lying postures (both supine and prone) on varied terrains such as grass slopes and stone tile.

	Sim2Real	Task		Smoothness			Safety
	Sim2Real	Success $\uparrow$	Task Metric $\uparrow$	Action Jitter $\downarrow$	DoF Pos Jitter $\downarrow$	Energy $\downarrow$	$\mathcal{S}^{\text{Torque}}_{0.8,0.5}\uparrow$	$\mathcal{S}^{\text{DoF}}_{0.8,0.5}\uparrow$
❶ Getting Up from Supine Poses
Tao et al. [65]	✗	92.62 $\pm$ 0.54	1.27 $\pm$ 0.00	5.39 $\pm$ 0.01	0.48 $\pm$ 0.00	650.19 $\pm$ 1.26	0.72 $\pm$ 3.10e-4	0.73 $\pm$ 1.39e-4
HumanUP w/o Stage II	✗	24.82 $\pm$ 0.25	0.83 $\pm$ 0.00	13.70 $\pm$ 0.18	0.71 $\pm$ 0.00	1311.22 $\pm$ 8.57	0.57 $\pm$ 1.45e-3	0.67 $\pm$ 5.56e-4
HumanUP w/o Full URDF	✗	93.95 $\pm$ 0.24	1.22 $\pm$ 0.00	0.71 $\pm$ 0.00	0.11 $\pm$ 0.00	104.14 $\pm$ 0.57	0.92 $\pm$ 8.36e-5	0.77 $\pm$ 9.40e-5
HumanUP w/o Posture Rand.	✓	65.39 $\pm$ 0.50	1.09 $\pm$ 0.04	0.75 $\pm$ 0.05	0.15 $\pm$ 0.03	141.52 $\pm$ 0.61	0.91 $\pm$ 2.32e-4	0.74 $\pm$ 7.24e-5
HumanUP w/ Hard Symmetry	✓	84.56 $\pm$ 0.11	1.23 $\pm$ 0.00	0.97 $\pm$ 0.01	0.22 $\pm$ 0.00	182.39 $\pm$ 0.22	0.89 $\pm$ 1.70e-5	0.78 $\pm$ 8.81e-5
HumanUP	✓	95.34 $\pm$ 0.12	1.24 $\pm$ 0.00	0.56 $\pm$ 0.01	0.10 $\pm$ 0.00	91.74 $\pm$ 0.33	0.93 $\pm$ 1.55e-5	0.78 $\pm$ 4.15e-5
❷ Rolling Over from Prone to Supine Poses
HumanUP w/o Stage II	✗	43.48 $\pm$ 0.41	0.91 $\pm$ 0.00	3.32 $\pm$ 0.31	0.40 $\pm$ 0.05	1684.66 $\pm$ 0.43	0.65 $\pm$ 6.28e-4	0.72 $\pm$ 7.18e-5
HumanUP w/o Full URDF	✗	87.73 $\pm$ 0.33	0.97 $\pm$ 0.00	0.33 $\pm$ 0.00	0.07 $\pm$ 0.00	59.01 $\pm$ 0.05	0.93 $\pm$ 7.91e-5	0.75 $\pm$ 9.98e-5
HumanUP w/o Posture Rand.	✓	37.27 $\pm$ 1.14	0.77 $\pm$ 0.01	0.77 $\pm$ 0.01	0.15 $\pm$ 0.00	234.46 $\pm$ 1.00	0.90 $\pm$ 4.98e-4	0.72 $\pm$ 2.04e-4
HumanUP w/ Hard Symmetry	✓	75.53 $\pm$ 0.25	0.60 $\pm$ 0.00	0.31 $\pm$ 0.00	0.09 $\pm$ 0.00	84.95 $\pm$ 0.33	0.95 $\pm$ 3.12e-5	0.76 $\pm$ 2.49e-5
HumanUP	✓	94.40 $\pm$ 0.21	0.99 $\pm$ 0.00	0.31 $\pm$ 0.00	0.06 $\pm$ 0.00	57.08 $\pm$ 0.20	0.95 $\pm$ 1.51e-4	0.76 $\pm$ 2.48e-5
❸ Getting Up from Prone Poses
Tao et al. [65]^†	✗	98.99 $\pm$ 0.20	1.26 $\pm$ 0.00	11.73 $\pm$ 0.01	0.76 $\pm$ 0.00	1015.27 $\pm$ 0.65	0.67 $\pm$ 2.24e-4	0.68 $\pm$ 6.41e-5
HumanUP w/o Stage II	✗	27.59 $\pm$ 0.28	1.23 $\pm$ 0.00	5.56 $\pm$ 0.36	0.45 $\pm$ 0.04	1213.07 $\pm$ 5.56	0.67 $\pm$ 4.71e-3	0.71 $\pm$ 2.17e-3
HumanUP w/o Full URDF	✗	89.59 $\pm$ 0.29	0.82 $\pm$ 0.00	0.44 $\pm$ 0.01	0.08 $\pm$ 0.00	77.61 $\pm$ 0.86	0.92 $\pm$ 2.88e-5	0.75 $\pm$ 3.19e-5
HumanUP w/o Posture Rand.	✓	30.25 $\pm$ 0.24	0.87 $\pm$ 0.02	1.05 $\pm$ 0.01	0.15 $\pm$ 0.00	208.23 $\pm$ 1.27	0.90 $\pm$ 3.06e-4	0.73 $\pm$ 1.01e-4
HumanUP w/ Hard Symmetry	✓	67.12 $\pm$ 0.34	1.09 $\pm$ 0.01	0.94 $\pm$ 0.01	0.23 $\pm$ 0.01	196.17 $\pm$ 3.68	0.91 $\pm$ 3.54e-5	0.76 $\pm$ 4.45e-5
HumanUP	✓	92.10 $\pm$ 0.46	1.24 $\pm$ 0.00	0.39 $\pm$ 0.01	0.07 $\pm$ 0.00	69.98 $\pm$ 0.45	0.94 $\pm$ 1.82e-4	0.77 $\pm$ 3.70e-4

🔼 Table I presents simulation results comparing the performance of the proposed HumanUP method with several baseline methods on a held-out test set of supine and prone robot poses. HumanUP’s two-stage training approach is evaluated, along with ablations removing key components. A comparison is also made with a baseline method from prior work which directly solves the final task without an intermediate rolling-over stage. The results show success rates, task metrics (height and body uprightness), smoothness metrics (action and DoF position jitter, energy consumption), and safety metrics (torque and DoF limits). A ‘Sim2Real’ column indicates which methods successfully transferred to real-world testing.
read the caption
TABLE I: Simulation results. We compare HumanUP with several baselines on the held-out split of our curated posture set 𝒫supinesubscript𝒫supine\mathcal{P}_{\text{supine}}caligraphic_P start_POSTSUBSCRIPT supine end_POSTSUBSCRIPT and 𝒫pronesubscript𝒫prone\mathcal{P}_{\text{prone}}caligraphic_P start_POSTSUBSCRIPT prone end_POSTSUBSCRIPT using full URDF. All methods are trained on the training split of our posture set 𝒫𝒫\mathcal{P}caligraphic_P, except for methods HumanUP w/o Stage II and w/o posture randomization. HumanUP solves task ❸ by solving task ❷ and task ❶ consecutively. We do not include the results of baseline 6 (HumanUP w/o Two-Stage Learning) as it cannot solve the task. † Tao et al. [65] is trained to directly solving task ❸ as it does not have a rolling over policy. Sim2Real column indicates whether the method can transfer to the real world successfully. We tested all methods in the real world for which the Smoothness and Safety metrics are reasonable, and Sim2Real is false if deployment wasn’t successful. Metrics are introduced in Section V-C.

In-depth insights
#

Sim-to-Real RL
#

Sim-to-Real Reinforcement Learning (RL) is a crucial technique for training robots to perform complex tasks in the real world. It leverages the efficiency of simulation for training, but faces the challenge of transferring the learned policies effectively to real-world scenarios. Bridging the reality gap between simulation and reality is paramount and requires careful consideration of various factors. These include accurate physics modeling within the simulator, domain randomization to expose the agent to variability not present in a perfectly controlled environment, and appropriate reward functions that translate well to the real world. Curriculum learning can significantly improve the training process by gradually increasing the difficulty of the tasks and allowing the agent to master fundamental skills before tackling more complex ones. Another critical aspect is ensuring the learned policy is robust and generalizable, able to adapt to unforeseen variations in the environment or robot’s initial state. Despite the challenges, Sim-to-Real RL offers a promising path for developing adaptable and robust robotic control policies, capable of handling the complexities and uncertainties inherent in real-world operations.

Curriculum Learning
#

Curriculum learning, a pedagogical approach where simpler tasks precede more complex ones, is crucial for the success of the humanoid robot getting-up task. The paper cleverly employs a two-stage curriculum. Stage I, focusing on motion discovery, prioritizes finding any successful getting-up trajectory with minimal constraints on smoothness or speed. This allows the robot to learn the fundamental sequence of actions necessary to stand up without being bogged down by complex constraints, enabling faster initial learning. Stage II then refines these initial motions, prioritizing deployability. This involves improving smoothness and speed, applying strong control regularization and domain randomization. The introduction of this two-stage approach is innovative, addressing the unique challenges of humanoid getting-up which are different from typical locomotion tasks. By starting with simpler, less constrained tasks and gradually increasing complexity and adding robustness, the method cleverly leverages the strengths of curriculum learning, resulting in a more efficient and generalizable policy that is directly transferable to real-world scenarios.

Contact-Rich Locomotion
#

Contact-rich locomotion presents a significant challenge in robotics, demanding advanced control strategies beyond traditional methods. The complexity arises from the numerous and dynamic contact points between the robot and its environment, unlike simpler locomotion tasks. This necessitates accurate modeling of collision geometry and contact forces, which is computationally expensive and difficult to generalize. Reward functions in reinforcement learning become sparse and under-specified, posing difficulties in training effective policies. Approaches like curriculum learning, which progressively increase the difficulty of the training environment, and two-stage training, which first focuses on task discovery and then on refinement, show promise in addressing this challenge. However, transferring learned policies from simulation to the real world remains a significant hurdle due to differences in dynamics and environmental factors. Future research will need to focus on improving contact modeling, developing more robust and generalizable reward functions, and bridging the simulation-to-reality gap for effective contact-rich locomotion in real-world applications.

Humanoid Fall Recovery
#

Humanoid fall recovery presents a significant challenge in robotics, demanding robust and adaptable solutions. Current approaches range from hand-engineered controllers, which struggle with the complexity and variability of falls and terrains, to learning-based methods. Learning-based approaches show promise, but face challenges such as contact modeling, sparse reward design, and generalization to unseen scenarios. The paper explores a two-stage reinforcement learning framework to overcome these challenges. Stage I focuses on trajectory discovery, prioritizing task completion over smoothness, while Stage II refines the trajectory for real-world deployment, emphasizing robustness and smooth motion. This two-stage approach, coupled with a curriculum of increasing complexity, demonstrates a successful real-world implementation on a Unitree G1 robot. Key innovations include techniques to address the challenges of complex contact patterns and sparse rewards unique to the getting-up task. However, limitations remain in simulator accuracy and the need for further research in generalizing to more diverse and unpredictable falls.

Two-Stage Policy
#

The proposed “Two-Stage Policy” framework offers a novel approach to training humanoid robot getting-up policies by breaking down the complex task into two simpler stages. Stage I, the discovery stage, focuses on learning a feasible trajectory without strict constraints, prioritizing task completion over smoothness or speed. This allows the robot to explore a wider range of motions and discover effective getting-up strategies. Stage II, the deployment stage, then refines this trajectory, incorporating constraints on smoothness, speed, and torque limits, resulting in a policy that’s both robust and safe for real-world deployment. This two-stage approach, coupled with curriculum learning that gradually increases the difficulty, significantly improves the success rate and generalizability of the learned policy. The separation of motion discovery from refinement is crucial because it addresses the challenge of balancing exploration and exploitation in reinforcement learning, enabling effective learning even in complex, contact-rich scenarios. This strategy avoids the pitfalls of directly training a deployable policy from the start, which often leads to poor performance due to premature convergence to suboptimal solutions.

More visual insights
#

More on figures

🔼 This figure details the HUMANUP system’s two-stage reinforcement learning approach for training humanoid robot getting-up policies. Stage I focuses on discovering an effective getting-up trajectory with minimal constraints, while Stage II refines this trajectory to create a deployable, robust, and generalizable policy that handles various terrains and starting poses. The two-stage process incorporates a curriculum, starting with simpler settings in Stage I (simplified collision model, fixed starting pose, weak regularization) and progressing to more complex scenarios in Stage II (full collision model, varied starting poses, strong regularization). The final policy is then directly deployed on a real-world robot.
read the caption
Figure 2: HumanUP system overview. Our getting-up policy (Section III-A) is trained in simulation using two-stage RL training, after which it is directly deployed in the real world. (a) Stage I (Section III-B1) learns a discovery policy f𝑓fitalic_f that figures out a getting-up trajectory with minimal deployment constraints. (b) Stage II (Section III-B2) converts the trajectory discovered by Stage I into a policy π𝜋\piitalic_π that is deployable, robust, and generalizable. This policy π𝜋\piitalic_π is trained by learning to track a slowed down version of the discovered trajectory under strong control regularization on varied terrains and from varied initial poses. (c) The two-stage training induces a curriculum (Section III-C). Stage I targets motion discovery in easier settings (simpler collision geometry, same starting poses, weak regularization, no variations in terrain), while Stage II solves the task of making the learned motion deployable and generalizable.

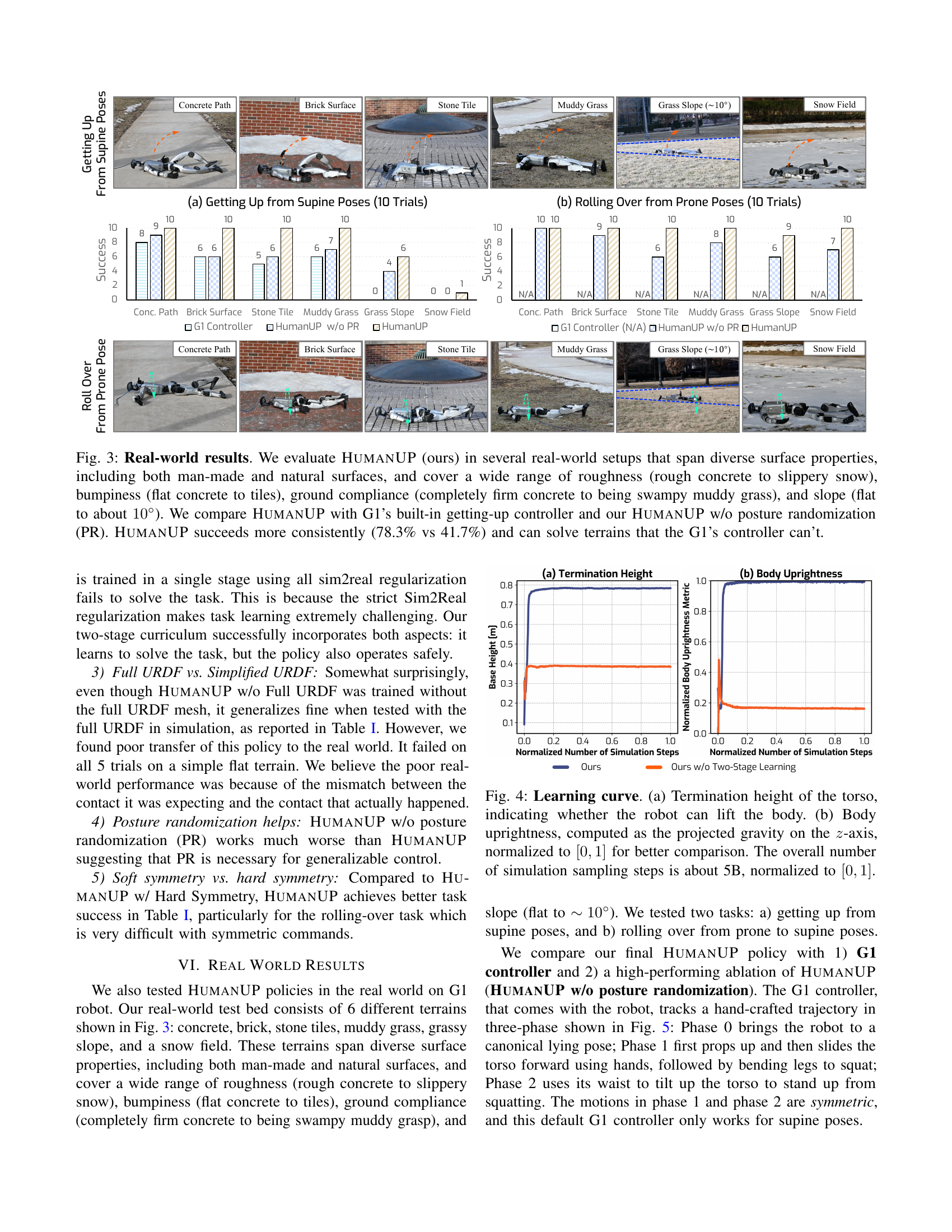
🔼 Figure 3 showcases the real-world performance evaluation of the HumanUP getting-up policy. The experiments were conducted on a Unitree G1 humanoid robot across six diverse terrains: concrete, brick, stone tiles, muddy grass, a grassy slope (approximately 10 degrees), and a snowfield. These terrains were selected to test the robustness of the policy against variations in surface roughness (smooth to very rough), bumpiness (flat to uneven), ground compliance (firm to soft), and slope. The results compare the success rate of HumanUP with the G1’s built-in getting-up controller and a version of HumanUP without posture randomization. The figure visually demonstrates HumanUP’s superior performance, achieving a significantly higher success rate (78.3%) compared to the G1 controller (41.7%) and showcasing its ability to successfully navigate terrains where the G1 controller fails.
read the caption
Figure 3: Real-world results. We evaluate HumanUP (ours) in several real-world setups that span diverse surface properties, including both man-made and natural surfaces, and cover a wide range of roughness (rough concrete to slippery snow), bumpiness (flat concrete to tiles), ground compliance (completely firm concrete to being swampy muddy grass), and slope (flat to about 10∘superscript1010^{\circ}10 start_POSTSUPERSCRIPT ∘ end_POSTSUPERSCRIPT). We compare HumanUP with G1’s built-in getting-up controller and our HumanUP w/o posture randomization (PR). HumanUP succeeds more consistently (78.3% vs 41.7%) and can solve terrains that the G1’s controller can’t.

🔼 Figure 4 presents the learning curves for two key metrics during the training process of the humanoid robot’s getting-up policy. The first metric, shown in (a), is the termination height of the robot’s torso, which represents how effectively the robot can lift its body during the getting-up motion. The second metric, displayed in (b), is the body uprightness, calculated as the projected gravity on the z-axis. This metric is normalized to a range of 0 to 1 to allow for easier comparison between different simulation runs and stages of training. The x-axis of both plots represents the normalized number of simulation steps, indicating the progress of the training process. The total number of simulation steps used in the training is approximately 5 billion. These curves illustrate the performance improvement over time and help in evaluating the effectiveness of the two-stage training approach.
read the caption
Figure 4: Learning curve. (a) Termination height of the torso, indicating whether the robot can lift the body. (b) Body uprightness, computed as the projected gravity on the z𝑧zitalic_z-axis, normalized to [0,1]01[0,1][ 0 , 1 ] for better comparison. The overall number of simulation sampling steps is about 5B, normalized to [0,1]01[0,1][ 0 , 1 ].

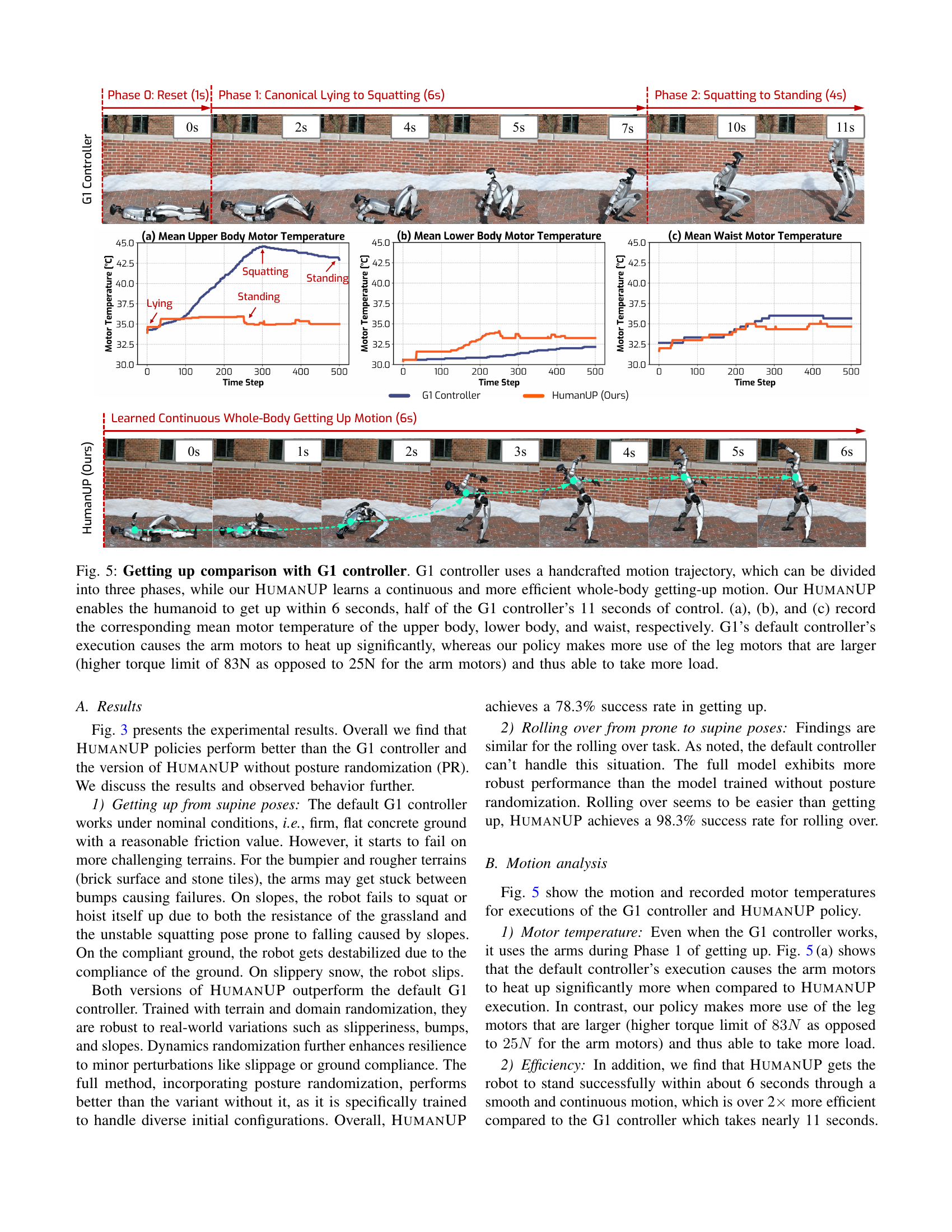
🔼 This figure compares the getting-up performance of the HumanUP method with that of the G1 controller. The G1 controller uses a pre-designed three-phase motion, while HumanUP learns a continuous, whole-body motion. HumanUP enables the robot to get up in 6 seconds, half the time taken by the G1 controller (11 seconds). The figure also displays the mean motor temperatures for the upper body, lower body, and waist. The G1 controller leads to excessive heating of the arm motors, while HumanUP utilizes the higher-torque leg motors more effectively, mitigating this issue.
read the caption
Figure 5: Getting up comparison with G1 controller. G1 controller uses a handcrafted motion trajectory, which can be divided into three phases, while our HumanUP learns a continuous and more efficient whole-body getting-up motion. Our HumanUP enables the humanoid to get up within 6 seconds, half of the G1 controller’s 11 seconds of control. (a), (b), and (c) record the corresponding mean motor temperature of the upper body, lower body, and waist, respectively. G1’s default controller’s execution causes the arm motors to heat up significantly, whereas our policy makes more use of the leg motors that are larger (higher torque limit of 83N as opposed to 25N for the arm motors) and thus able to take more load.

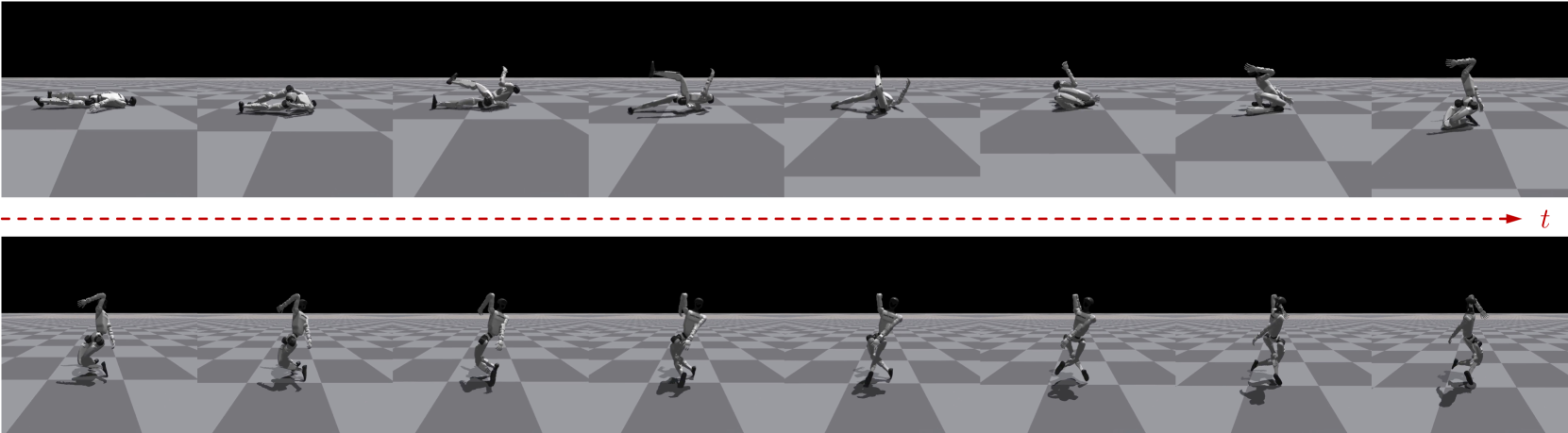
🔼 Figure 6 shows qualitative examples of how the G1 controller and the HumanUP policy fail on challenging terrains like grass slopes and snowy fields. The G1 controller struggles to squat on the slope due to high friction and insufficient torque, ultimately slipping on the snow. HumanUP, although capable of partially getting up on both surfaces, ultimately fails due to unstable foot placement on the slope and slippage on the snow. This highlights the challenges of robust fall recovery in diverse real-world conditions.
read the caption
Figure 6: Qualitative examples of failure modes on grass slope and snow field. G1 controller isn’t able to squat on the sloping grass and slips on the slow. HumanUP policy is able to partially get up on both the slope and the snow but falls due to unstable feet placement on the slope and slippage on the snow.

More on tables

Term	Expression	Weight
Penalty:
Torque limits	$\mathds{1}({{\boldsymbol{{\tau}}_{t}}\notin[\boldsymbol{\tau}_{\min},% \boldsymbol{\tau}_{\max}]})$	-0.1
DoF position limits	$\mathds{1}({{\boldsymbol{{d}}_{t}}\notin[\boldsymbol{q}_{\min},\boldsymbol{q}_% {\max}]})$	-5
Energy	$\lVert\ \boldsymbol{\tau}\odot\dot{\mathbf{q}}\rVert$	-1e-4
Termination	$\mathds{1}_{\text{termination}}$	-500
Regularization:
DoF acceleration	$\lVert{\boldsymbol{\ddot{d}}_{t}}\rVert_{2}$	-1e-7
DoF velocity	$\lVert{\boldsymbol{\dot{d}}_{t}}\rVert_{2}^{2}$	-1e-4
Action rate	$\lVert\boldsymbol{a}_{t}\rVert_{2}^{2}$	-0.1
Torque	$\lVert{\boldsymbol{{\tau}}_{t}}\rVert$	-6e-7
DoF position error	$\mathds{1}(h_{\text{base}}\geq 0.8)\cdot\exp\left(-0.05\\|{\boldsymbol{{d}}_{t}% }-{\boldsymbol{{d}}_{t}}^{\text{default}}\|\right)$	-0.75
Angular velocity	$\lVert\omega^{2}\rVert$	-0.1
Base velocity	$\lVert\boldsymbol{v}^{2}\rVert$	-0.1
Foot slip	$\mathds{1}(\boldsymbol{F}^{\text{feet}}_{z}>5.0)\cdot\sqrt{\\|\boldsymbol{v}_{z% }^{\text{feet}}\\|}$	-1
Getting-Up Task Rewards:
Base height exp	$\exp(\boldsymbol{h}^{base})-1$	5
Head height exp	$\exp(\boldsymbol{h}^{head})-1$	5
$\Delta$ base height	$\mathds{1}(\boldsymbol{h}_{t}^{base}>\boldsymbol{h}^{base}_{t-1})$	1
Feet contact forces reward	$\mathds{1}(\lVert\boldsymbol{F}_{t}^{feet}\rVert>\lVert\boldsymbol{F}^{\text{% feet}}_{t-1})\rVert$	1
Standing on feet reward	$\mathds{1}\big{(}(\lVert\boldsymbol{F}^{\text{feet}}\rVert>0\big{)}\&\big{(}% \boldsymbol{h}^{\text{feet}}<0.2)\big{)}$	2.5
Body upright reward	$\exp(-\mathbf{g}^{\text{base}}_{z})$	0.25
Feet height reward	$\exp(-10\cdot\boldsymbol{h}^{\text{feet}})$	2.5
Feet distance reward	$\frac{1}{2}\Big{(}\exp(-100\left\|\max(\boldsymbol{d}_{\text{feet}}-\boldsymbol% {d}_{\min},-0.5)\right\|)$ $+\exp(-100\left\|\max(\boldsymbol{d}_{\text{feet}}-\boldsymbol{d}_{\max},0)% \right\|)\Big{)}$	2
Foot orientation	$\sqrt{\lVert G_{xy}^{\text{feet}}\rVert}$	-0.5
Soft body symmetry penalty	$\left\\|\mathbf{a}_{\text{left}}-\mathbf{a}_{\text{right}}\right\\|$	-1.0
Soft waist symmetry penalty	$\left\\|\mathbf{a}^{\text{waist}}\right\\|$	-1.0
Rolling-Over Task Rewards:
Base Gravity Exp	$\frac{1}{2}\Big{(}\exp\big{(}-0.01(1-\cos\theta_{\text{left}})\big{)}+$ $\exp\big{(}-0.01(1-\cos\theta_{\text{right}})\big{)}\Big{)},$ $\cos\theta=\frac{\mathbf{g}^{\text{knee}}\cdot\mathbf{g}_{\text{target}}}{\\|% \mathbf{g}^{\text{base}}\\|\\|\mathbf{g}_{\text{base}}\\|}$	8
Knee Gravity Exp	$\frac{1}{2}\Big{(}\exp\big{(}-0.01(1-\cos\theta_{\text{left}})\big{)}+$ $\exp\big{(}-0.01(1-\cos\theta_{\text{right}})\big{)}\Big{)},$ $\cos\theta=\frac{\mathbf{g}^{\text{knee}}\cdot\mathbf{g}_{\text{target}}}{\\|% \mathbf{g}^{\text{base}}\\|\\|\mathbf{g}_{\text{base}}\\|}$	8
Feet distance reward	$\frac{1}{2}\Big{(}\exp(-100\left\|\max(\boldsymbol{d}_{\text{feet}}-\boldsymbol% {d}_{\min},-0.5)\right\|)$ $+\exp(-100\left\|\max(\boldsymbol{d}_{\text{feet}}-\boldsymbol{d}_{\max},0)% \right\|)\Big{)}$	2
Feet height reward	$\exp(-10\cdot\boldsymbol{h}^{\text{feet}})$	2.5

🔼 Table II details the reward function components and their weights used in Stage I of the HUMANUP training process. The reward function is designed with three key parts: 1. Penalty Rewards: These discourage undesirable behaviors that could hinder the successful transfer of the learned policy from simulation to the real world. Specific penalties are applied for exceeding torque limits, exceeding joint position limits, and excessive energy consumption. 2. Regularization Rewards: These encourage smoother and more controlled motions, making the learned policy more robust and deployable in real-world scenarios. They help to refine the motions making them suitable for deployment on a real robot. 3. Task Rewards: These incentivize the robot to successfully complete the getting-up or rolling-over task. These rewards directly encourage the desired behavior of getting up or rolling over to a standing posture.
read the caption
TABLE II: Reward components and weights in Stage I. Penalty rewards prevent undesired behaviors for sim-to-real transfer, regularization refines motion, and task rewards ensure successful getting up or rolling over.

Term	Expression	Weight
Penalty:
Torque limits	$\mathds{1}({{\boldsymbol{{\tau}}_{t}}\notin[\boldsymbol{\tau}_{\min},% \boldsymbol{\tau}_{\max}]})$	-5
Ankle torque limits	$\mathds{1}({{\boldsymbol{{\tau}}_{t}}^{\text{ankle}}\notin[\boldsymbol{\tau}^{% \text{ankle}}_{\min},\boldsymbol{\tau}^{\text{ankle}}_{\max}]})$	-0.01
Upper torque limits	$\mathds{1}({{\boldsymbol{{\tau}}_{t}}^{\text{upper}}\notin[\boldsymbol{\tau}^{% \text{upper}}_{\min},\boldsymbol{\tau}^{\text{upper}}_{\max}]})$	-0.01
DoF position limits	$\mathds{1}({{\boldsymbol{{d}}_{t}}\notin[\boldsymbol{q}_{\min},\boldsymbol{q}_% {\max}]})$	-5
Ankle DoF position limits	$\mathds{1}({{\boldsymbol{{d}}_{t}}^{\text{ankle}}\notin[\boldsymbol{q}^{\text{% ankle}}_{\min},\boldsymbol{q}^{\text{ankle}}_{\max}]})$	-5
Upper DoF position limits	$\mathds{1}({{\boldsymbol{{d}}_{t}}^{\text{upper}}\notin[\boldsymbol{q}^{\text{% upper}}_{\min},\boldsymbol{q}^{\text{upper}}_{\max}]})$	-5
Energy	$\lVert\ \boldsymbol{\tau}\odot\dot{\mathbf{q}}\rVert$	-1e-4
Termination	$\mathds{1}_{\text{termination}}$	-50
Regularization:
DoF acceleration	$\lVert{\boldsymbol{\ddot{d}}_{t}}\rVert_{2}$	-1e-7
DoF velocity	$\lVert{\boldsymbol{\dot{d}}_{t}}\rVert_{2}^{2}$	-1e-3
Action rate	$\lVert\boldsymbol{a}_{t}\rVert_{2}^{2}$	-0.1
Torque	$\lVert{\boldsymbol{{\tau}}_{t}}\rVert$	-0.003
Ankle torque	$\lVert{\boldsymbol{{\tau}}_{t}}^{\text{ankle}}\rVert$	-6e-7
Upper torque	$\lVert{\boldsymbol{{\tau}}_{t}}^{\text{upper}}\rVert$	-6e-7
Angular velocity	$\lVert\omega^{2}\rVert$	-0.1
Base velocity	$\lVert\boldsymbol{v}^{2}\rVert$	-0.1
Tracking Rewards:
Tracking DoF position	$\exp\left(-\frac{({\boldsymbol{{d}}_{t}}-{\boldsymbol{{d}}_{t}}^{\text{target}% })^{2}}{4}\right)$	8
Feet distance reward	$\frac{1}{2}\Big{(}\exp(-100\left\|\max(\boldsymbol{d}_{\text{feet}}-\boldsymbol% {d}_{\min},-0.5)\right\|)$ $+\exp(-100\left\|\max(\boldsymbol{d}_{feet}-\boldsymbol{d}_{\max},0)\right\|)% \Big{)}$	2
Foot orientation	$\sqrt{\lVert\mathbf{g}_{xy}^{\text{feet}}\rVert}$	-0.5

🔼 This table details the reward function components and their corresponding weights used in Stage II of the HUMANUP training process. The reward function is designed to guide the humanoid robot’s learning in several ways. Penalty rewards discourage undesired behaviors, such as exceeding torque limits or joint displacement limits, that would hinder successful transfer from simulation to the real world. Regularization rewards promote smooth and controlled movements, which enhances the deployability and robustness of the learned policy. Finally, task rewards incentivize the robot to successfully track the desired whole-body getting-up motion in real-time. The weights assigned to each component reflect their relative importance in the overall learning objective.
read the caption
TABLE III: Reward components and weights in Stage II. Penalty rewards prevent undesired behaviors for sim-to-real transfer, regularization refines motion, and task rewards ensure successful whole-body tracking in real time.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Sim-to-Real RL#

Curriculum Learning#

Contact-Rich Locomotion#

Humanoid Fall Recovery#

Two-Stage Policy#

More visual insights#

Full paper#