TL;DR#
Scaling effective context length is vital for AGI, but traditional attention mechanisms face quadratic complexity. Current solutions involve biased structures or linear approximations, which impacts complex reasoning. This paper tackles the challenge by adhering to the “less structure” principle, enabling models to autonomously decide where to focus, sidestepping predefined biases.
The paper introduces Mixture of Block Attention(MoBA), which brings MoE principles to attention mechanisms. MoBA demonstrates superior performance on long-context tasks and smoothly transitions between full and sparse attention to boost efficiency. Deployed in Kimi, MoBA showcases progress in LLM attention computation and is available at https://github.com/MoonshotAI/MoBA.
Key Takeaways#
Why does it matter?#
This paper introduces MoBA, which is a mixture of block attention for long-context LLMs. This is important because it enhances efficiency without compromising performance. It also opens up possibilities for integrating existing models without significant retraining costs, establishing a direction for developing long-context capabilities in LLMs.
Visual Insights#

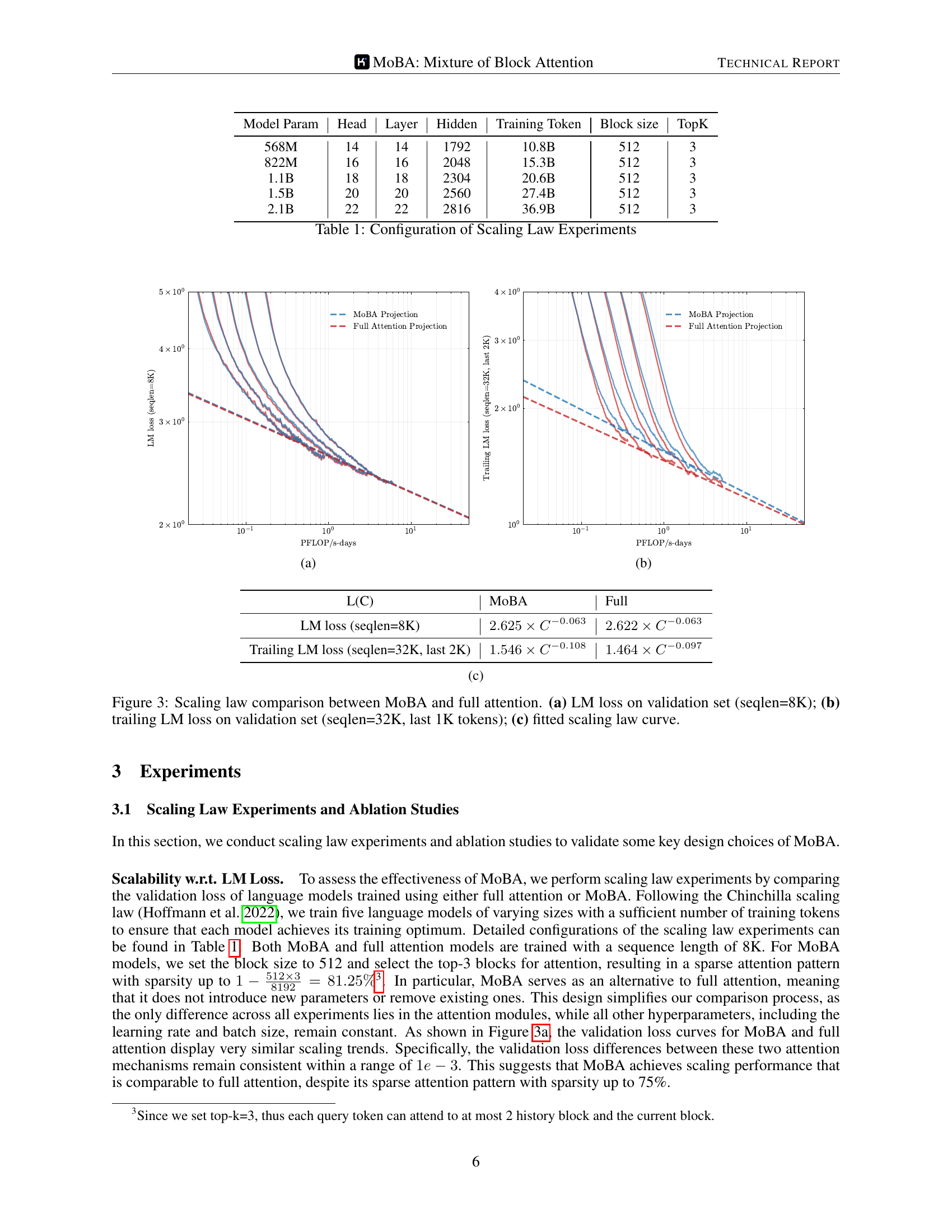
🔼 The figure shows the scaling law comparison between Mixture of Block Attention (MOBA) and full attention. Specifically, it plots the language modeling (LM) loss on the validation set against the PFLOP/s-days, a measure of computational cost. The plot shows that both MOBA and full attention exhibit similar scaling trends, demonstrating that MOBA achieves comparable scaling performance despite employing a sparse attention mechanism.
read the caption
(a)
| Model Param | Head | Layer | Hidden | Training Token | Block size | TopK |
|---|---|---|---|---|---|---|
| 568M | 14 | 14 | 1792 | 10.8B | 512 | 3 |
| 822M | 16 | 16 | 2048 | 15.3B | 512 | 3 |
| 1.1B | 18 | 18 | 2304 | 20.6B | 512 | 3 |
| 1.5B | 20 | 20 | 2560 | 27.4B | 512 | 3 |
| 2.1B | 22 | 22 | 2816 | 36.9B | 512 | 3 |
🔼 This table presents the configurations used in the scaling law experiments. For each model size, it shows the number of model parameters, the number of attention heads, the number of layers, the hidden dimension size, the total number of training tokens used, the block size used in the MOBA (Mixture of Block Attention) approach (if applicable), and the top-k hyperparameter for MOBA (also only if applicable). This information details the experimental setup used to evaluate the scaling behavior of the language models.
read the caption
Table 1: Configuration of Scaling Law Experiments
In-depth insights#
MOBA: Long Context#
MOBA’s architecture excels in processing long contexts by selectively attending to relevant blocks of information. Traditional attention mechanisms face quadratic complexity with increasing sequence length, making them computationally expensive for long contexts. MOBA addresses this by partitioning the context into blocks and employing a gating mechanism to dynamically select the most informative blocks for each query token. This approach mimics the Mixture of Experts (MoE) paradigm, enabling a more efficient computation without sacrificing performance. By focusing on relevant blocks, MOBA reduces the computational burden, making it feasible to process extremely long sequences. This capability is crucial for tasks like document summarization, question answering, and machine translation, where understanding the context is essential for generating accurate results. MOBA’s ability to handle long contexts effectively opens new possibilities for large language models, allowing them to tackle more complex and nuanced tasks.
Less Structure#
The ’less structure’ principle in the context of attention mechanisms highlights the advantage of allowing the model to autonomously learn where to attend, rather than imposing predefined biases or structures. This approach contrasts with methods like sink attention or sliding window attention, which, while efficient, can limit the model’s generalizability by restricting its focus to specific areas of the input sequence. The goal is to maximize model flexibility and adaptability, enabling it to discover and leverage relevant patterns without being constrained by human-engineered assumptions. This approach can also enable the model to identify complex relationships that might be missed by more rigid structures. It is important to note that by enabling the model to autonomously learn which points in the context it should attend to the model may take more computational time and resources. While this principle aims for greater flexibility, it necessitates careful design to ensure the model learns efficiently and effectively, avoiding potential pitfalls like overfitting or ignoring crucial contextual information.
Efficient Scaling#
Efficient scaling in LLMs is critical due to the quadratic complexity of attention. Innovations like sparse attention and MoE are vital to reduce computational costs while maintaining performance. Approaches range from static patterns (e.g., fixed attention) to dynamic methods (e.g., routing transformers), each offering trade-offs. The choice depends on sequence length, resources, and the balance between efficiency and performance. Future work should explore novel selection strategies, modality applications, and generalization improvements, to achieve more efficient and scalable LLMs. MoBA serves as an effective and balanced framework to address this limitation. High throughput can be accomplished due to the method’s memory-efficiency and the efficient computation.
Hybrid Attention#
Hybrid attention likely refers to combining different attention mechanisms, potentially mixing global and local attention. This could mean integrating sparse and dense methods to balance computational efficiency with performance. Layer-wise application is a common strategy, utilizing different attention types in different network layers. Dynamic switching between attention mechanisms based on input characteristics is another possibility. Improved long-range dependency capture while maintaining local context awareness is a likely goal. Computational cost reduction and adaptability to various tasks are key benefits, enabling efficient processing of long sequences and complex relationships within the data.
Future Directions#
Given the context of efficient attention mechanisms for large language models (LLMs), future directions could explore more adaptive block selection strategies within MOBA. This could involve dynamic adjustment of block sizes based on content complexity or task demands. Further research should investigate the application of MOBA to other modalities beyond text, such as images or video, to assess its generalizability. Moreover, exploring the combination of MOBA with other efficient attention techniques, like linear attention or attention sinks, might yield further performance improvements. A crucial aspect is the investigation of MOBA’s potential in enhancing the reasoning capabilities of LLMs, particularly in tasks requiring complex contextual understanding. Finally, future work could focus on developing more sophisticated gating mechanisms within MOBA, potentially incorporating learned routing functions or hierarchical gating structures, leading to enhanced efficiency and scalability, and ultimately enhancing the ability to tackle increasingly complex tasks while maintaining efficiency.
More visual insights#
More on figures

🔼 This figure shows the scaling law comparison between MOBA and full attention for the trailing LM loss on a validation set with a sequence length of 32K, focusing on the last 2K tokens. It visually represents the relationship between computational cost (PFLOP/s-days) and the trailing LM loss for both MOBA and full attention models of varying sizes. The plot helps to understand how the loss changes as the model size and computational resources increase, providing insights into the efficiency and scalability of MOBA compared to the traditional full attention mechanism in the context of processing long sequences.
read the caption
(b)
🔼 Figure 1 illustrates the Mixture of Block Attention (MoBA) architecture. (a) shows a simplified example of MoBA in action, demonstrating how query tokens attend to only a subset of key-value blocks rather than the entire context, enabling efficient processing of long sequences. A gating network dynamically selects the relevant blocks for each query. (b) shows how MoBA integrates with FlashAttention, a high-performance attention mechanism, to further enhance computational efficiency.
read the caption
Figure 1: Illustration of mixture of block attention (MoBA). (a) A running example of MoBA; (b) Integration of MoBA into Flash Attention.

🔼 This figure shows the scaling law comparison between MOBA and full attention for LM loss on the validation set with a sequence length of 8K. The x-axis represents the computation (PFLOP/s-days), while the y-axis represents the LM loss. Two curves, one for MOBA and one for full attention, show how loss changes with increasing computational resources. The figure helps to demonstrate the scalability and efficiency of the MOBA model by comparing it to the full attention model.
read the caption
(a)

🔼 This figure shows the scaling law comparison between MOBA and full attention for the trailing LM loss on the validation set. The sequence length is 32K, and only the last 2K tokens’ loss is considered. The x-axis represents the training FLOPs in PFLOPs-days, and the y-axis represents the trailing LM loss. The plot shows the loss curves for MOBA and full attention methods. This helps to evaluate the long context capability of MOBA by looking at the loss of the final tokens in a sequence.
read the caption
(b)

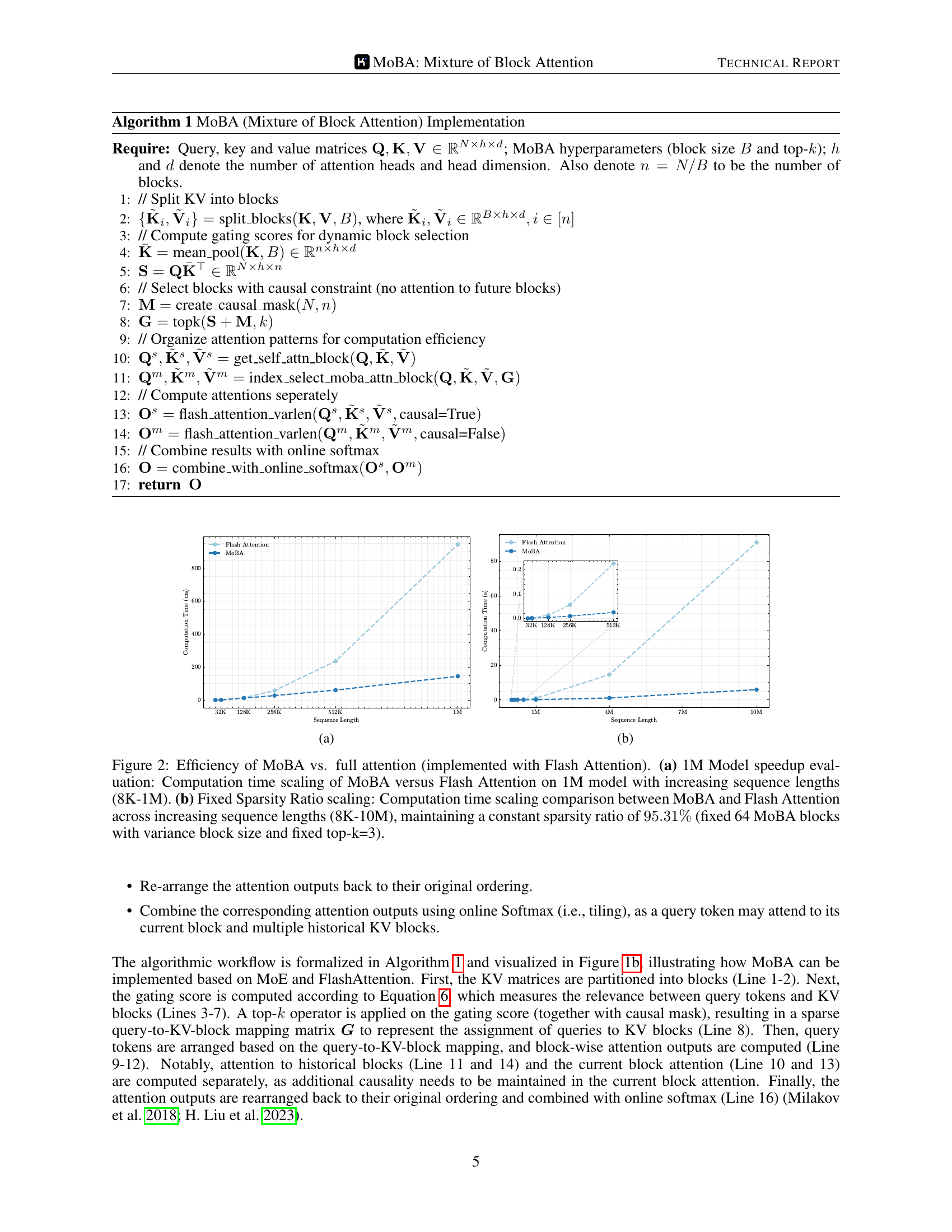
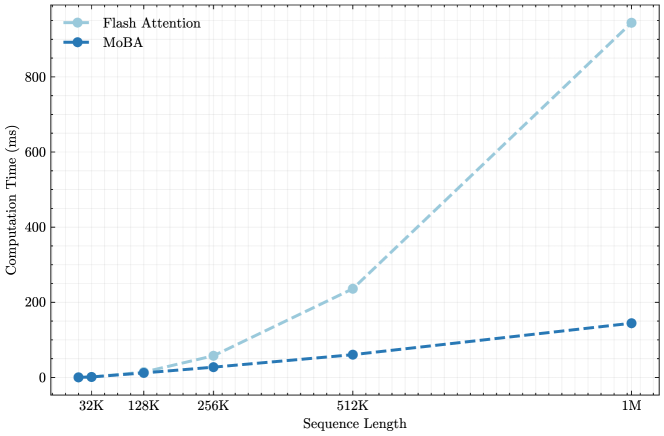
🔼 Figure 2 presents a comparison of the computational efficiency of Mixture of Block Attention (MOBA) against standard full attention, both implemented using Flash Attention. Subfigure (a) shows the speedup achieved by MOBA compared to full attention on a 1M parameter model across increasing sequence lengths (8K to 1M tokens). Subfigure (b) demonstrates the scaling behavior while maintaining a consistent sparsity ratio of approximately 95.31% by adjusting block sizes and keeping the number of MoBA blocks fixed at 64 and top-k fixed at 3. This figure highlights MOBA’s ability to achieve significant speedups over traditional full attention, particularly beneficial for longer sequences while controlling sparsity.
read the caption
Figure 2: Efficiency of MoBA vs. full attention (implemented with Flash Attention). (a) 1M Model speedup evaluation: Computation time scaling of MoBA versus Flash Attention on 1M model with increasing sequence lengths (8K-1M). (b) Fixed Sparsity Ratio scaling: Computation time scaling comparison between MoBA and Flash Attention across increasing sequence lengths (8K-10M), maintaining a constant sparsity ratio of 95.31%percent95.3195.31\%95.31 % (fixed 64 MoBA blocks with variance block size and fixed top-k=3).

🔼 This figure shows the scaling law comparison between MOBA and full attention for the LM loss on the validation set with a sequence length of 8K. The x-axis represents the compute (PFLOP/s-days), and the y-axis represents the LM loss. The plot shows the loss curves for both MOBA and full attention models. The figure visually demonstrates that MOBA achieves a comparable performance to that of full attention, even with its sparse attention pattern.
read the caption
(a)

🔼 This figure displays the scaling law comparison between Mixture of Block Attention (MOBA) and full attention, specifically focusing on the trailing Language Model (LM) loss on a validation set with a sequence length of 32K, considering only the last 1K tokens. It visually represents the relationship between the computational cost (PFLOP/s-days) and the trailing LM loss for both MOBA and full attention models of varying sizes. The graph helps assess the efficiency and long-context capabilities of MOBA by comparing how well each method handles long sequences and how the loss scales with increasing computational resources.
read the caption
(b)

🔼 This figure displays the scaling law comparison between MOBA and full attention. Specifically, it shows the trailing LM loss on the validation set (sequence length = 32K, last 2K tokens). The fitted scaling law curve is also shown, illustrating the relationship between compute (in PFLOP/s-days) and LM loss. The plot allows one to observe how the loss changes for both the MOBA and Full Attention methods as the compute resources increase.
read the caption
(c)

🔼 This figure displays the results of scaling law experiments comparing MoBA (Mixture of Block Attention) and Full Attention mechanisms. Subfigure (a) shows the Language Model (LM) loss on a validation set using sequences of length 8K. Subfigure (b) presents the trailing LM loss, focusing on the last 1K tokens of sequences with length 32K, which assesses the model’s ability to accurately generate the concluding part of long sequences. Finally, subfigure (c) illustrates the fitted scaling law curve derived from the experimental data, showing the relationship between compute and model performance for both MoBA and Full Attention.
read the caption
Figure 3: Scaling law comparison between MoBA and full attention. (a) LM loss on validation set (seqlen=8K); (b) trailing LM loss on validation set (seqlen=32K, last 1K tokens); (c) fitted scaling law curve.

🔼 This figure displays the results of an ablation study on the impact of different block granularities in the Mixture of Block Attention (MoBA) model. The experiment used a 1.5B parameter model with a 32K context length. Various block sizes (8, 16, 32, 64, and 128) and corresponding top-k values (2, 4, 8, 16, and 32) were used to maintain a constant 75% sparsity. The LM loss on the validation set is plotted against the different block granularities. This allows for an assessment of the model’s performance with varying levels of granularity in block segmentation.
read the caption
Figure 4: Fine-Grained Block Segmentation. The LM loss on validation set v.s. MoBA with different block granularity.

🔼 This figure shows the scaling law comparison between MOBA and full attention in terms of LM loss on the validation set with a sequence length of 8K. The x-axis represents the compute (PFLOP/s-days), and the y-axis represents the LM loss. Two lines are plotted, one for MOBA and another for full attention. The figure demonstrates that MOBA achieves scaling performance comparable to full attention.
read the caption
(a)

🔼 The figure shows the scaling law comparison between MOBA and full attention in terms of trailing LM loss (on validation set, sequence length = 32K, last 1K tokens). It displays the relationship between the computational cost (PFLOP/s-days) and the trailing LM loss for models trained with MOBA and with full attention. The plot helps to visualize the efficiency gains achieved by using MOBA, especially when dealing with longer sequences. The scaling law curve shows that MoBA achieves comparable performance to full attention while using significantly less computation.
read the caption
(b)

🔼 This figure displays the fitted scaling law curve, comparing the loss between MOBA and full attention models across different computational costs (PFLOP/s-days). The x-axis represents the computational cost, while the y-axis shows the language model loss. The plot visualizes the relationship between computational resources and model performance for both MOBA and full attention.
read the caption
(c)

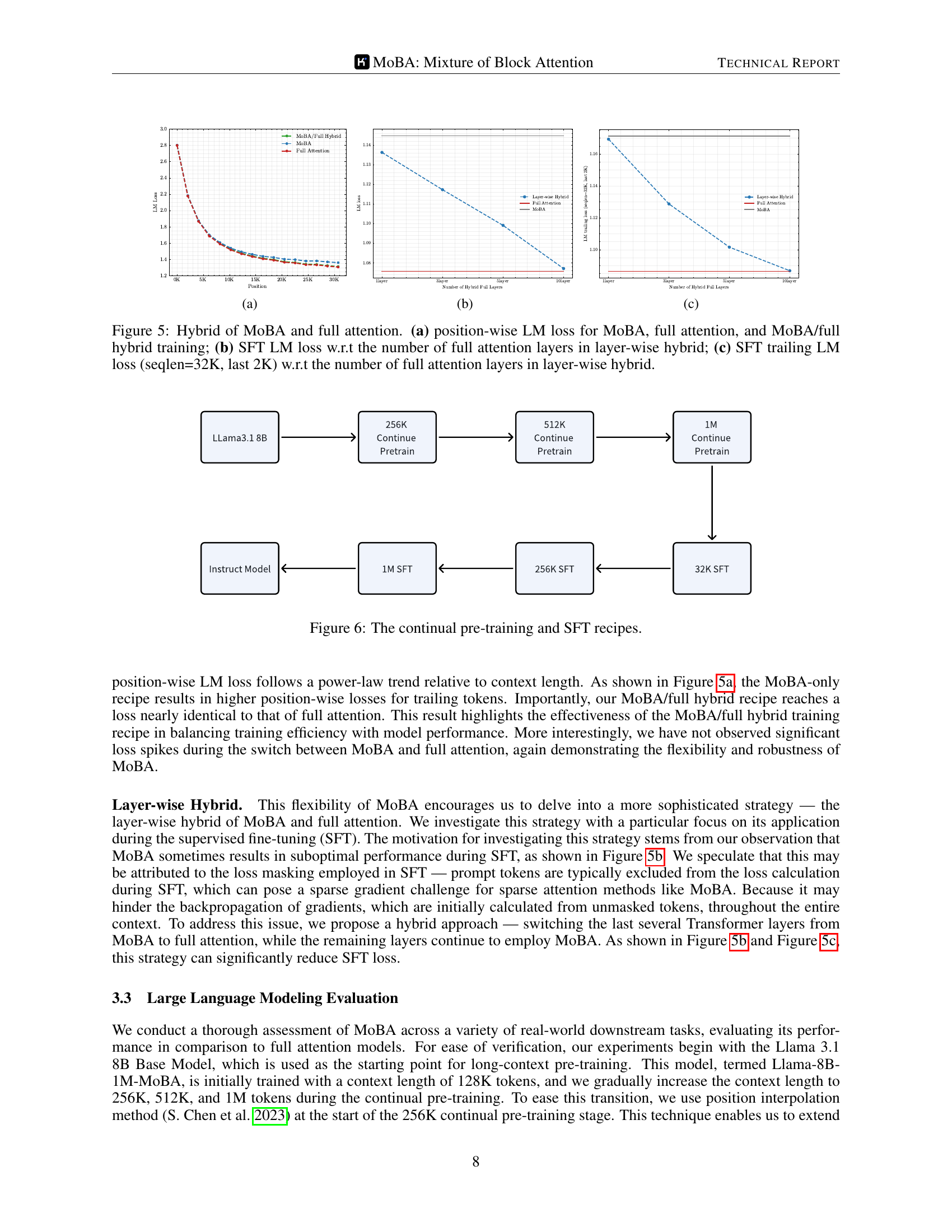
🔼 Figure 5 presents a comparison of three different training approaches: using only MoBA, using only full attention, and a hybrid approach that combines both. Panel (a) displays the position-wise LM loss across a sequence. Panels (b) and (c) analyze the impact of progressively incorporating full attention layers during supervised fine-tuning (SFT). Panel (b) shows the SFT LM loss while (c) shows the SFT trailing LM loss specifically focusing on the last 2K tokens of a 32K sequence, providing insights into the models’ ability to generate long sequences effectively.
read the caption
Figure 5: Hybrid of MoBA and full attention. (a) position-wise LM loss for MoBA, full attention, and MoBA/full hybrid training; (b) SFT LM loss w.r.t the number of full attention layers in layer-wise hybrid; (c) SFT trailing LM loss (seqlen=32K, last 2K) w.r.t the number of full attention layers in layer-wise hybrid.

🔼 Figure 6 illustrates the training pipeline used for the continual pre-training and subsequent supervised fine-tuning (SFT) of language models. The continual pre-training stage involves gradually increasing the context length (from 256K to 1M tokens) through a series of pre-training phases. After each pre-training phase, supervised fine-tuning is performed with increasingly large context lengths (from 32K to 1M tokens). This figure visually represents the steps involved in this iterative training process, clarifying the context window expansion at each stage and depicting the transitions between pre-training and SFT.
read the caption
Figure 6: The continual pre-training and SFT recipes.

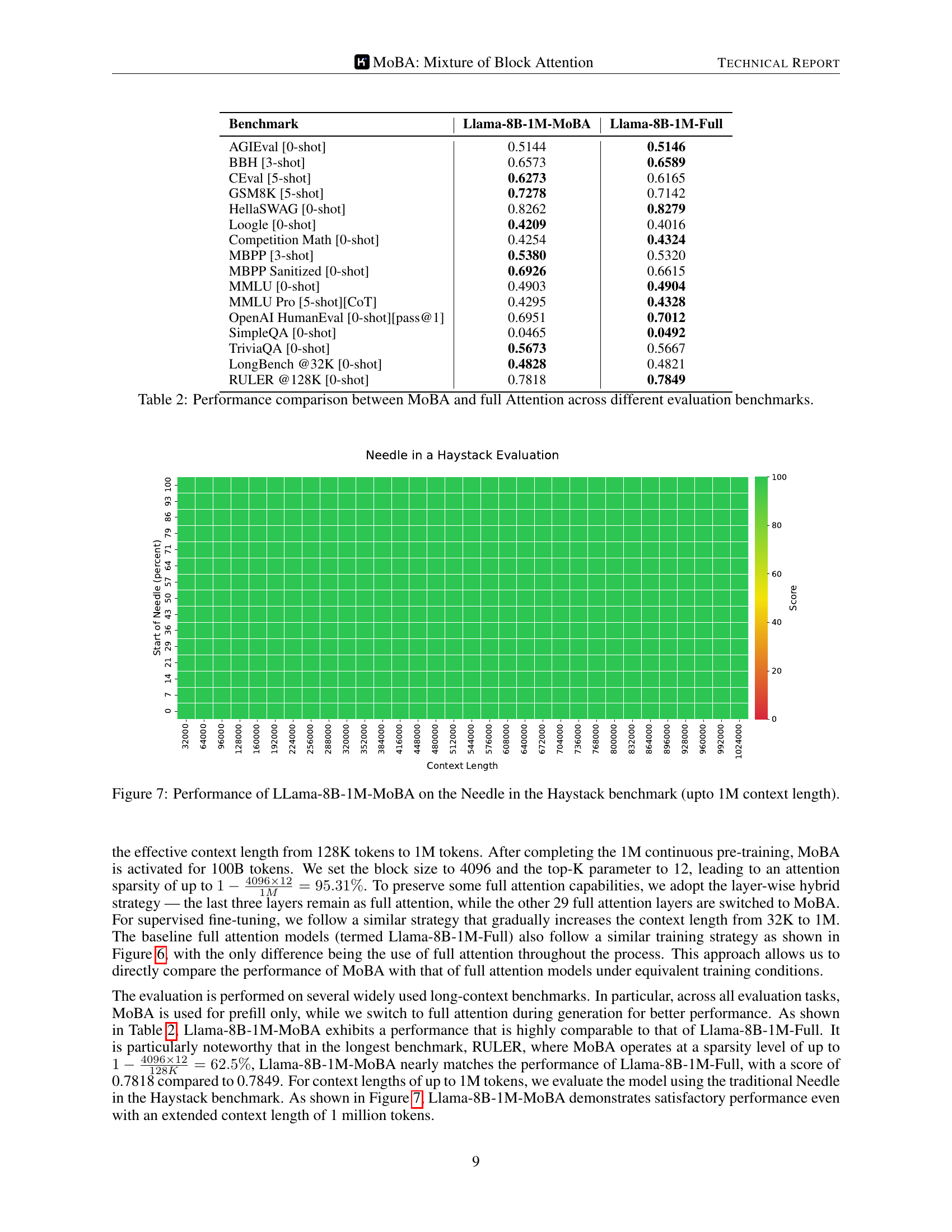
🔼 This figure displays the performance of the Llama-8B-1M-MoBA model on the Needle in a Haystack benchmark. The Needle in a Haystack benchmark tests a model’s ability to find a specific piece of information within a large context. The x-axis represents the context length (up to 1 million tokens), and the y-axis shows the performance score. The heatmap visualization makes it easy to see how the model’s performance changes as the context length increases. This experiment demonstrates the model’s ability to effectively process extremely long contexts.
read the caption
Figure 7: Performance of LLama-8B-1M-MoBA on the Needle in the Haystack benchmark (upto 1M context length).

🔼 This figure displays the scaling law for the initial 2000 tokens. It shows the relationship between the computational cost (PFLOP/s-days) and the loss achieved by models using MOBA (Mixture of Block Attention) versus full attention. The x-axis represents the computational cost, and the y-axis represents the loss. The graph shows two curves, one for MOBA and one for the full attention approach, allowing comparison of the performance and efficiency of the two methods for this portion of the sequence.
read the caption
(a) Scaling law (0-2k)

🔼 This figure shows the scaling law for positions 2000-4000. It plots the PFLOP/s-days (floating point operations per second-days, a measure of computational cost) against the LM Loss (language model loss, a measure of model performance). Two lines are shown: one for the MOBA (Mixture of Block Attention) model and one for a full attention model. The lines illustrate the relationship between computational cost and model performance for different model sizes in this specific token range. The slope of the lines indicates how the loss changes as computational cost increases.
read the caption
(b) Scaling law (2-4k)

🔼 This figure shows the scaling law for positions 4000-6000, comparing the performance of MoBA and full attention in terms of LM loss and PFLOP/s-days. The x-axis represents the computational cost (PFLOP/s-days), and the y-axis represents the LM loss. The lines represent different model sizes, and the plot illustrates how the LM loss scales with computational resources for both MoBA and full attention.
read the caption
(c) Scaling law (4-6k)

🔼 This figure shows the scaling law for positions 6000 to 8000. It plots the PFLOP/s-days (performance) against the LM Loss (training loss) for both MoBA (Mixture of Block Attention) and Full Attention models. The lines represent different model sizes, illustrating how training loss changes with compute and model size for each approach. This helps determine the efficiency and scaling behavior of MoBA relative to traditional full attention mechanisms for long sequences.
read the caption
(d) Scaling law (6-8k)

🔼 This figure shows the scaling law for positions 8000 to 10000. It plots the PFLOP/s-days against the LM loss for both MOBA (Mixture of Block Attention) and Full Attention models. The graph illustrates how the computational cost (PFLOP/s-days) scales with the language model loss (LM loss) for different model sizes in this specific range of token positions within a sequence. It helps to assess the computational efficiency of MOBA compared to traditional Full Attention in a particular region of the sequence being processed.
read the caption
(e) Scaling law (8-10k)

🔼 This figure shows the scaling law for positions 10k-12k. It is part of a set of figures (Figure 8) demonstrating scaling laws for various ranges of token positions (0-16k and 16-32k) and comparing the performance of MOBA and full attention models across different computational costs. The x-axis represents the computational cost (PFLOP/s-days), and the y-axis represents the LM loss. The curves show the relationship between computational resources and model performance for both MOBA and the full-attention baseline.
read the caption
(f) Scaling law (10-12k)

🔼 This figure is part of a scaling law experiment comparing MOBA and Full Attention. Specifically, it shows the relationship between PFLOP/s-days (a metric related to computational cost) and LM loss (a measure of model performance) for the token positions 12000-14000 in the training data. It demonstrates how the model performance changes as computational resources are scaled, allowing assessment of both MOBA’s efficiency and scalability compared to the baseline Full Attention mechanism.
read the caption
(g) Scaling law (12-14k)

🔼 This figure shows the scaling law for positions 14,000 to 16,000. It presents the relationship between compute (PFLOP/s-days) and LM loss for both the MOBA (Mixture of Block Attention) and Full Attention models. The plot helps visualize how the loss changes with varying computational resources, offering insights into the efficiency of MOBA compared to traditional full attention. The lines represent the results from different model sizes.
read the caption
(h) Scaling law (14-16k)

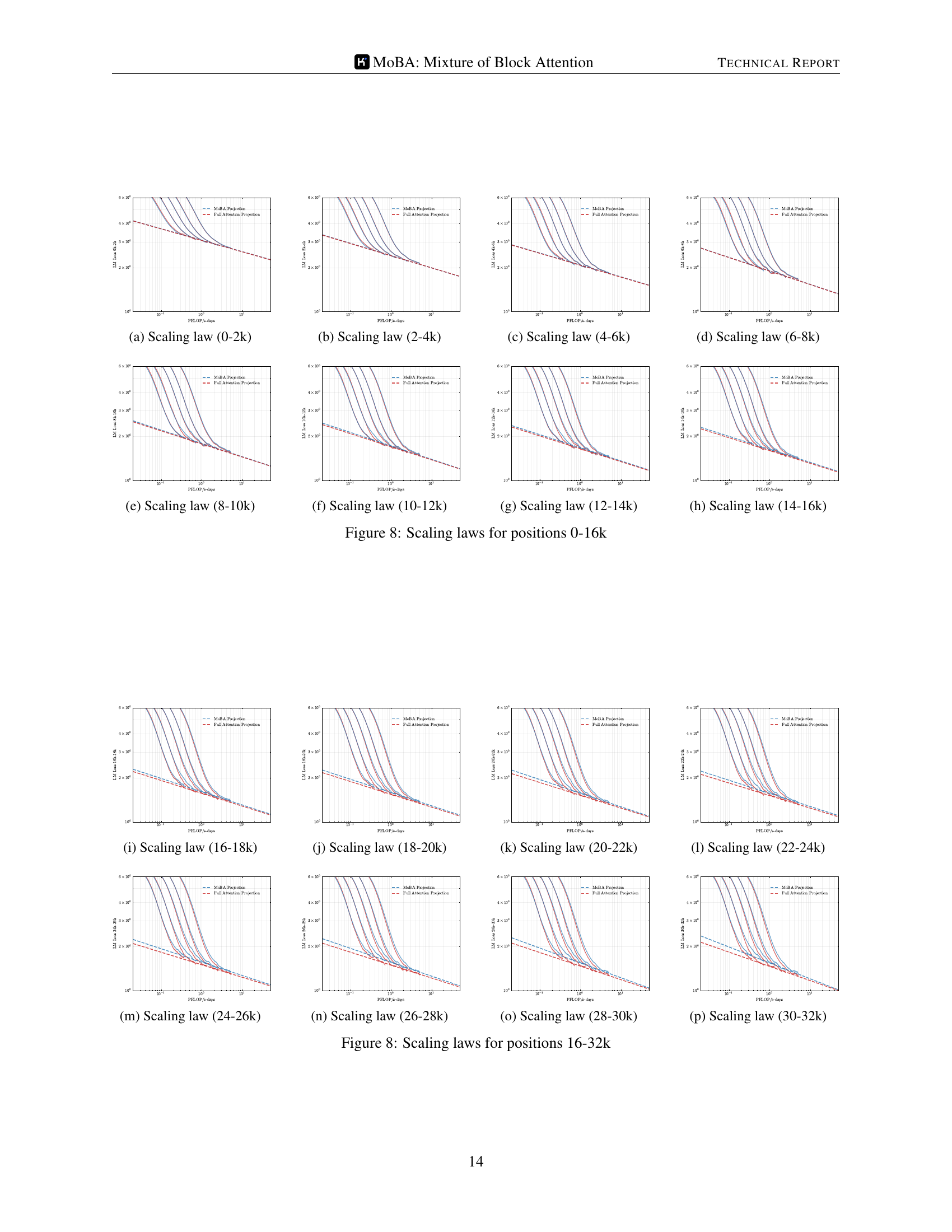
🔼 This figure displays scaling laws for different positions within the context window, specifically from position 0 to 16k. It shows the relationship between the computational cost (in PFLOP/s-days) and the loss of the language model. The plots are separated into subfigures (a) through (h), each covering a 2k-token range within the 0-16k span. Each subfigure presents the scaling laws for both MOBA (Mixture of Block Attention) and full attention models. By comparing the curves for MOBA and full attention across different parts of the context window, we can analyze how efficiently MOBA uses computational resources while maintaining performance comparable to full attention.
read the caption
Figure 8: Scaling laws for positions 0-16k

🔼 This figure presents the scaling law for positions 16,000 to 18,000 in the context of a large language model. It showcases the relationship between the computational resources (PFLOP/s-days) and the resulting loss (LM Loss) using two different attention mechanisms: MoBA (Mixture of Block Attention) and Full Attention. The graph allows for a visual comparison of the performance and efficiency of both mechanisms at this specific context window within the model.
read the caption
(i) Scaling law (16-18k)

🔼 This figure shows the scaling law for positions 18k to 20k in a language model. It plots the performance (likely LM loss) of the model against the computational resources (PFLOP/s-days). Two lines are shown, one for the model using the proposed Mixture of Block Attention (MOBA) and another for the model using full attention. The graph illustrates how the loss changes with increasing computational resources for the specified position range within the text sequence. This helps assess the efficiency and scalability of MOBA compared to the traditional full attention mechanism for long sequences.
read the caption
(j) Scaling law (18-20k)
More on tables
| L(C) | MoBA | Full |
|---|---|---|
| LM loss (seqlen=8K) | ||
| Trailing LM loss (seqlen=32K, last 2K) |
🔼 This table presents a quantitative comparison of the performance achieved by two different attention mechanisms: Mixture of Block Attention (MOBA) and Full Attention. The comparison is conducted across a range of established evaluation benchmarks commonly used to assess the capabilities of large language models (LLMs). Each benchmark assesses different aspects of LLM performance, offering a holistic view of how the two methods compare in various tasks.
read the caption
Table 2: Performance comparison between MoBA and full Attention across different evaluation benchmarks.
| Benchmark | Llama-8B-1M-MoBA | Llama-8B-1M-Full |
|---|---|---|
| AGIEval [0-shot] | 0.5144 | 0.5146 |
| BBH [3-shot] | 0.6573 | 0.6589 |
| CEval [5-shot] | 0.6273 | 0.6165 |
| GSM8K [5-shot] | 0.7278 | 0.7142 |
| HellaSWAG [0-shot] | 0.8262 | 0.8279 |
| Loogle [0-shot] | 0.4209 | 0.4016 |
| Competition Math [0-shot] | 0.4254 | 0.4324 |
| MBPP [3-shot] | 0.5380 | 0.5320 |
| MBPP Sanitized [0-shot] | 0.6926 | 0.6615 |
| MMLU [0-shot] | 0.4903 | 0.4904 |
| MMLU Pro [5-shot][CoT] | 0.4295 | 0.4328 |
| OpenAI HumanEval [0-shot][pass@1] | 0.6951 | 0.7012 |
| SimpleQA [0-shot] | 0.0465 | 0.0492 |
| TriviaQA [0-shot] | 0.5673 | 0.5667 |
| LongBench @32K [0-shot] | 0.4828 | 0.4821 |
| RULER @128K [0-shot] | 0.7818 | 0.7849 |
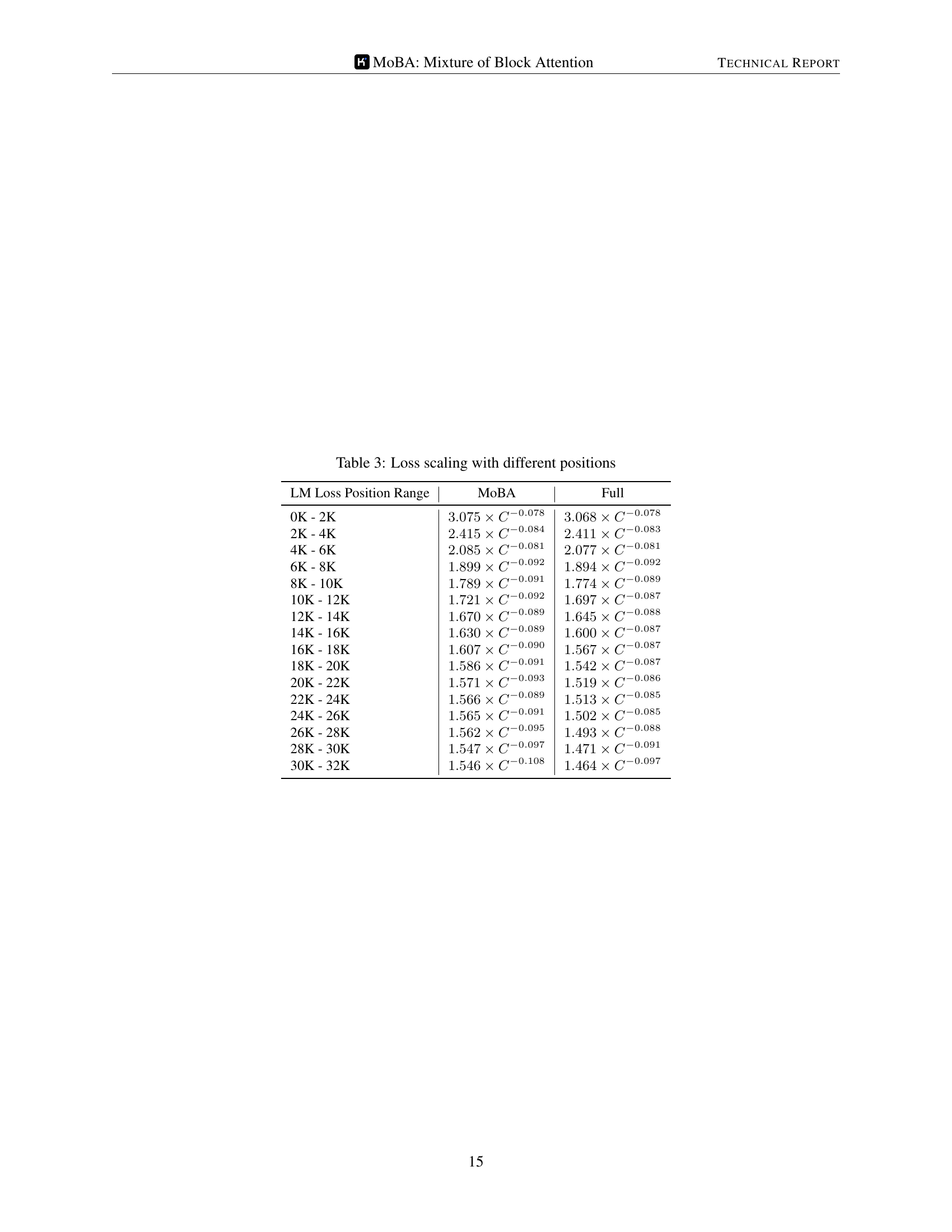
🔼 This table presents the scaling law for the loss of language models trained with different attention mechanisms (MOBA and Full Attention) across various sequence length ranges (from 0k to 32k tokens). It shows the relationship between the computational cost (in PFLOPs/day) and the resulting loss, providing insights into the efficiency and scalability of MOBA compared to the traditional full attention mechanism. For each sequence length range, the table gives fitted scaling law curves for both MOBA and Full Attention, allowing for a direct comparison of their performance.
read the caption
Table 3: Loss scaling with different positions
Full paper#