Self-rewarding correction for mathematical reasoning

2502.19613

Wei Xiong et el.

🤗 2025-02-28

TL;DR
#

This paper addresses the challenge of improving self-correction in Large Language Models (LLMs) without relying on external reward models. Current LLMs struggle with intrinsic self-correction, requiring complex multi-agent systems for error detection and refinement. This increases computational costs and deployment complexity. This paper aims to equip a single LLM with the ability to autonomously evaluate its reasoning and correct errors, simplifying the process and reducing computational overhead.

The paper introduces a self-rewarding reasoning framework and a two-stage algorithmic approach. The first stage involves synthesizing data that contain both self-rewarding and self-correcting mechanisms. The second stage uses reinforcement learning with rule-based signals to improve response accuracy and refine outputs. Results on Llama-3 and Qwen-2.5 show that the approach outperforms intrinsic self-correction and achieves performance comparable to systems that rely on external reward models.

Key Takeaways
#

Why does it matter?
#

This paper is important for researchers because it introduces an efficient self-rewarding reasoning LLM, which can lead to more streamlined and cost-effective AI deployment. It addresses the limitations of current LLMs and offers a new approach that could potentially be applied to a wide range of reasoning tasks. It paves the way for further research into improving intrinsic self-correction capabilities.

Visual Insights
#

Benchmark	Method	Turn 1	Final Accuracy	$\Delta(t_{1},t_{2})$	$\Delta^{i\to c}(t_{1},t_{2})$	$\Delta^{c\to i}(t_{1},t_{2})$
	Single-turn STaR/RAFT	77.0	77.0	-	-	-
	Single-turn DPO	76.8	76.8	-	-	-
	Single-turn PPO	79.4	79.4	-	-	-
	Prompt with Gold RM^†	65.4	66.8	1.4	1.4	0.0
	Intrinsic self-correction^†	65.4	51.4	-14.0	1.4	15.4
MATH500	STaR/RAFT for self-correction^†	71.6	70.4	-1.2	5.0	6.2
	STaR/RAFT+ for self-correction^†	72.0	71.2	-0.8	3.0	3.8
	Self-rewarding IFT	72.6	77.2	4.6	5.0	0.4
	Self-rewarding IFT + DPO w correctness	72.8	78.6	5.8	6.0	0.2
	Self-rewarding IFT + PPO w correctness	75.8	80.2	4.4	4.8	0.4
	Single-turn STaR/RAFT	40.1	40.1	-	-	-
	Single-turn DPO	39.0	39.0	-	-	-
	Single-turn PPO	39.5	39.5	-	-	-
	Prompt with Gold RM^†	23.4	25.6	2.2	2.2	0
	Intrinsic self-correction^†	23.4	18.1	-5.3	2.2	7.5
OlympiadBench	STaR/RAFT for self-correction ^†	36.5	32.5	-4.0	7.2	11.2
	STaR/RAFT+ for self-correction^†	35.7	35.5	-0.2	3.2	3.4
	Self-rewarding IFT	35.4	39.4	4.0	4.7	0.7
	Self-rewarding IFT + DPO w correctness	37.6	40.1	2.5	3.5	1.0
	Self-rewarding IFT + PPO w correctness	41.0	43.4	2.4	2.8	0.4
	Single-turn STaR/RAFT	32.0	32.0	-	-	-
	Single-turn DPO	31.6	31.6	-	-	-
	Single-turn PPO	33.1	33.1	-	-	-
	Prompt with Gold RM^†	9.9	11.7	1.8	1.8	0
	Intrinsic self-correction^†	9.9	8.4	-1.5	1.8	3.3
Minerva Math	STaR/RAFT for self-correction^†	28.7	29.4	0.7	1.8	1.1
	STaR/RAFT+ for self-correction^†	25.7	25.3	-0.4	0.8	1.2
	Self-rewarding IFT	23.2	28.7	5.5	7.3	1.8
	Self-rewarding IFT + DPO w correctness	26.8	34.6	7.8	9.6	1.8
	Self-rewarding IFT + PPO w correctness	34.0	38.4	4.4	5.1	0.7

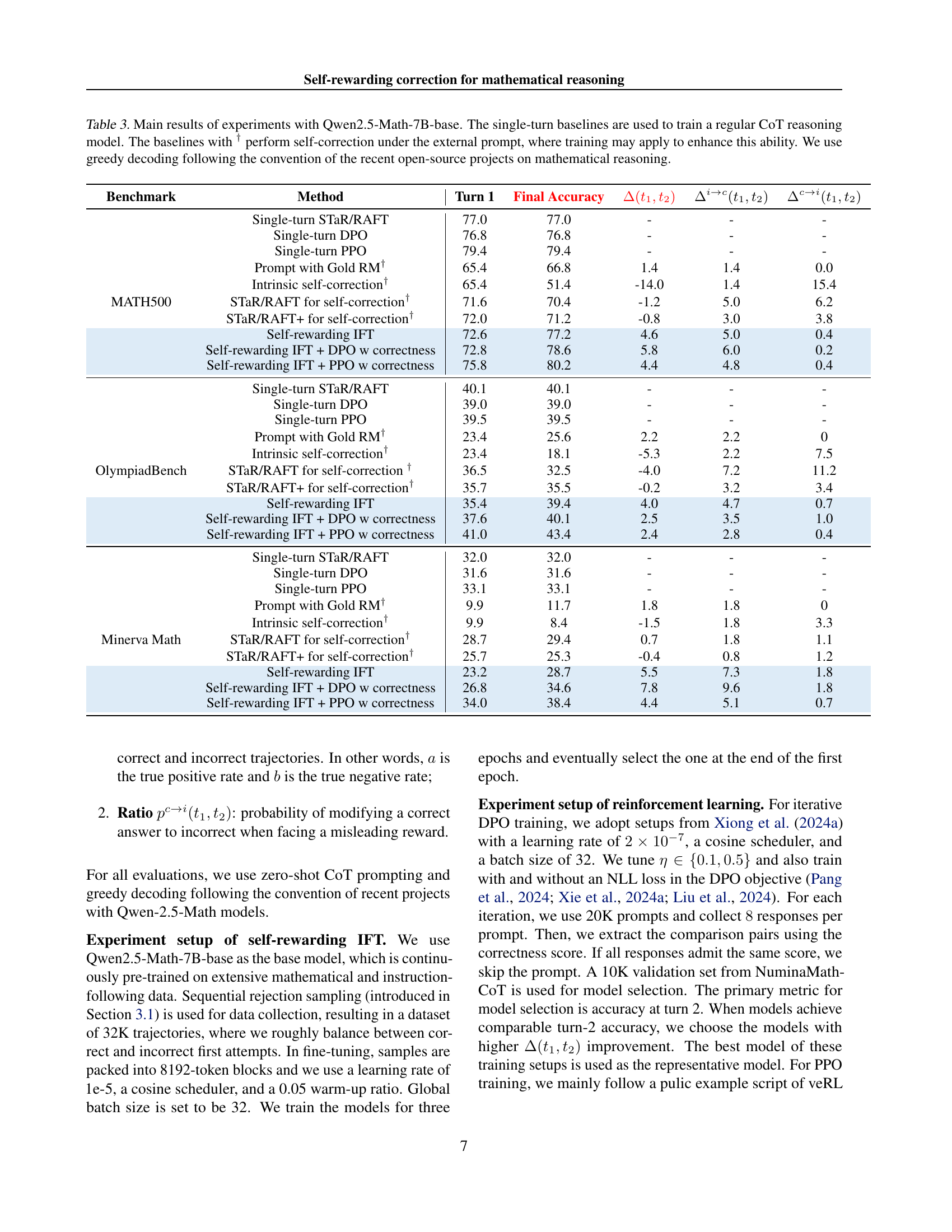
🔼 This table presents the results of experiments conducted using the Qwen2.5-Math-7B-base language model. It compares the performance of several different methods on three mathematical reasoning benchmarks: MATH500, OlympiadBench, and Minerva Math. The methods include single-turn baselines (without self-correction), baselines that employ self-correction with an external prompt (and potentially additional training to enhance self-correction abilities), and the proposed self-rewarding approach. The table reports the accuracy of the model at the first turn and the final accuracy after iterative reasoning and correction, along with various metrics reflecting improvement in accuracy, specifically the changes in problem correctness status from the first turn to the final answer. Greedy decoding was used for all methods.
read the caption
Table 3: Main results of experiments with Qwen2.5-Math-7B-base. The single-turn baselines are used to train a regular CoT reasoning model. The baselines with † perform self-correction under the external prompt, where training may apply to enhance this ability. We use greedy decoding following the convention of the recent open-source projects on mathematical reasoning.

In-depth insights
#

Self-Reward Intro
#

Self-rewarding reasoning in LLMs is a promising area, enabling models to autonomously evaluate and refine their outputs. The traditional approach relies on external reward models, which increases computational costs and deployment complexity. The ideal scenario would involve a single LLM capable of both generating reasoning steps and assessing their correctness. Current LLMs struggle with intrinsic self-correction, highlighting the need for innovative training techniques. By incorporating self-evaluation mechanisms, models can make informed decisions about when to revise their responses, leading to more efficient and accurate reasoning without needing external feedback loops. This has significant implications for model deployment and scalability.

2-Stage Training
#

The two-stage training paradigm detailed in the paper is a very good method. First, the model should be trained using self-generated data, where the algorithm uses sequential rejection sampling. Fine-tuning models here help to detect the errors in previously generated attempts, and also allows for revisions. In the second stage, the patterns are enhanced using reinforcement learning, and using rule-based signals. This is a good method because it enhances a model’s ability to evaluate and correct its outputs without relying on external reward models. However, there should be more details about the actual implementation process.

Rejection Sampling
#

The technique of rejection sampling is pivotal for curating high-quality datasets, especially when dealing with sparse behaviors like self-correction in language models. By generating a multitude of responses and selectively retaining only those that meet predefined criteria, we can efficiently distill datasets that exhibit desired patterns. The key insight is that base models might inherently possess self-correction abilities, albeit sparsely. Rejection sampling allows us to amplify these sparse behaviors, creating a dataset where self-correction patterns are more prevalent. This targeted dataset can then be used to fine-tune models, enabling them to learn and internalize these patterns more effectively. Furthermore, the process can be strategically iterated, prompting models in separate steps and combining them into a single trajectory to enforce both self-rewarding and self-correction

Llama vs. Qwen
#

In the realm of open-source large language models (LLMs), Llama and Qwen represent prominent and contrasting architectures. Llama, known for its research-friendly licensing, has become a cornerstone for academic exploration and community-driven development. Its architecture emphasizes simplicity and scalability, fostering a vibrant ecosystem of fine-tuned variants and derivatives. Qwen, backed by a commercial entity, offers a compelling blend of performance and accessibility. It stands out as a high-performing open-source model. While Llama prioritizes transparency and ease of modification, Qwen focuses on delivering state-of-the-art capabilities, potentially with more complex architectural choices. The interplay between these two models fuels innovation, driving progress in both open research and practical applications. The choice between Llama and Qwen hinges on the specific needs: Llama for research flexibility, Qwen for readily available performance.

Future Work
#

Future work could focus on mitigating the lower reward model accuracy, possibly through techniques like model merging or by using a larger base model. Exploring SimPO for more accurate probability is also promising. Addressing the limited enhancement of self-correction ability in the RL stage suggests exploring multi-turn RL strategies to decouple the self-rewarding steps, making the agent capable to learn how to correct the error in the previous step rather than giving up entirely. This may involve the study of different prompt engineering methods to enhance self-correction or to increase the model performance.

More visual insights
#

More on tables

Method	MATH-500 C	MATH-500 W	OlympiadBench C	OlympiadBench W	Minerva Math C	Minerva Math W
Self-rewarding IFT	93.0	47.7	89.6	45.9	91.7	36.1
PPO Step 100	97.5	56.4	98.1	33.5	87.4	29.7
PPO Step 220 $(\star)$	98.6	47.6	97.8	39.3	94.2	32.4
DPO Iter 2	91.3	56.2	81.9	51.8	86.7	36.2
DPO Iter 5 $(\star)$	92.0	50.6	88.2	44.5	92.4	37.4

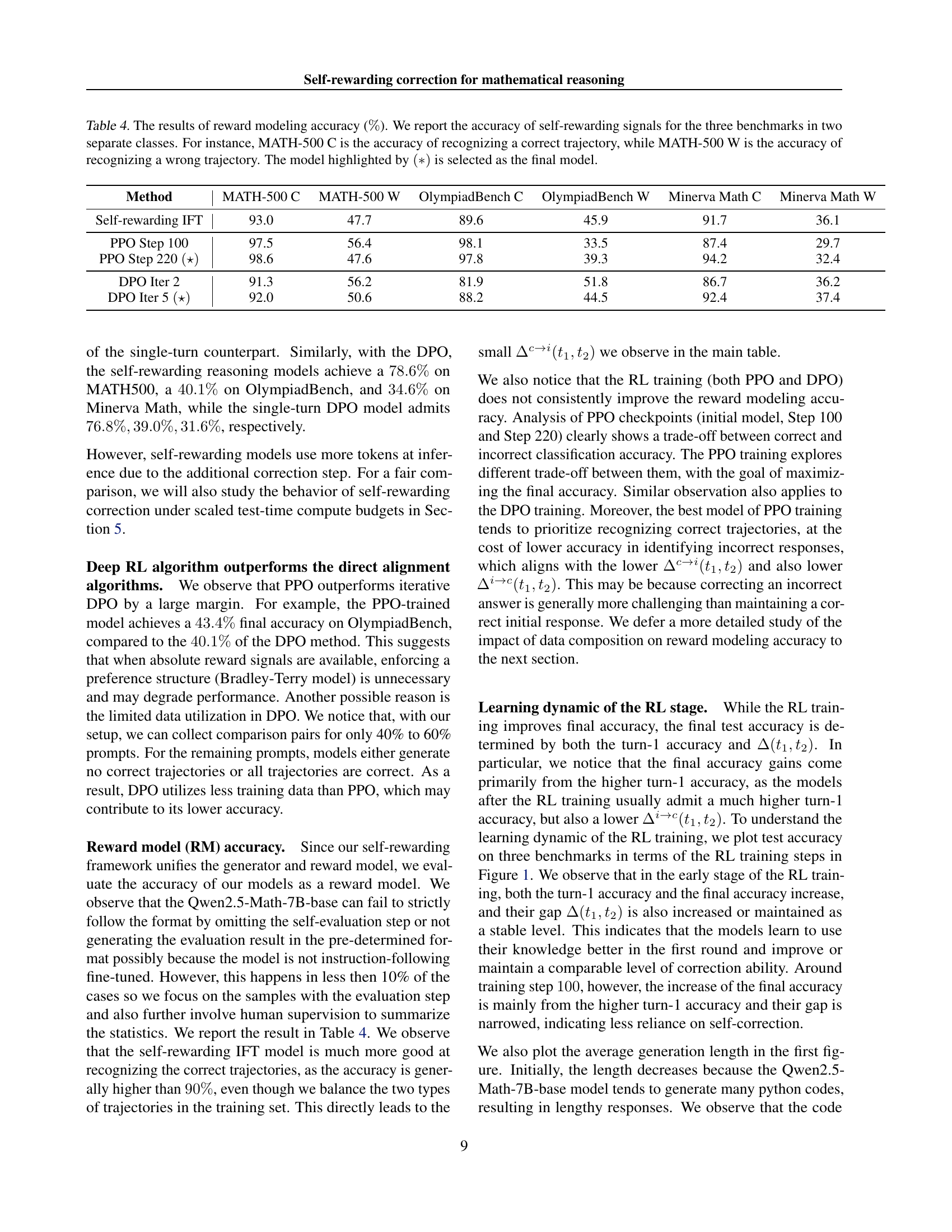
🔼 This table presents the performance of the reward models in evaluating the correctness of generated reasoning trajectories. It shows the accuracy of the models in identifying both correctly generated trajectories (C) and incorrectly generated trajectories (W) for three different mathematical reasoning benchmarks (MATH-500, OlympiadBench, and Minerva Math). The accuracy is reported separately for correctly and incorrectly generated sequences, providing a more detailed view of the model’s performance. The model marked with an asterisk (*) represents the final model selected for the study.
read the caption
Table 4: The results of reward modeling accuracy (%percent\%%). We report the accuracy of self-rewarding signals for the three benchmarks in two separate classes. For instance, MATH-500 C is the accuracy of recognizing a correct trajectory, while MATH-500 W is the accuracy of recognizing a wrong trajectory. The model highlighted by (∗)(*)( ∗ ) is selected as the final model.

Base Model	Method	Turn 1	Final Accuracy	$\Delta(t_{1},t_{2})$	$\Delta^{i\to c}(t_{1},t_{2})$	$\Delta^{c\to i}(t_{1},t_{2})$
Llama-3-8B-it	Prompt with Gold RM	20.7	30.3	9.6	9.6	0
Llama-3-8B-it	Prompt with External ORM	20.7	26.2	5.5	8.8	3.3
Llama-3-8B-it	Intrinsic self-correction	20.7	22.0	1.3	8.8	7.5
Llama-3-8B-it	STaR/RAFT for self-correction	22.3	26.1	3.7	11.4	7.7
Llama-3-8B-it	STaR/RAFT+ for self-correctio	22.7	27.1	4.4	11.7	7.3
Llama-3-8B-it	Self-rewarding IFT	22.6	27.9	5.3	8.8	3.5
Llama-3-8B-it	Self-rewarding IFT + Gold RM	22.6	33.9	11.3	11.3	0
Llama-3-SFT	Prompt with Gold RM	36.2	45.0	8.8	8.8	0
Llama-3-SFT	Prompt with External ORM	36.2	39.2	3.0	7.5	4.5
Llama-3-SFT	Intrinsic self-correction	36.2	35.3	-0.9	8.5	9.4
Llama-3-SFT	STaR/RAFT for self-correctio	38.5	36.7	-1.8	10.5	12.3
Llama-3-SFT	STaR/RAFT+ for self-correctio	37.9	38.8	0.9	9.4	8.5
Llama-3-SFT	Self-rewarding IFT	37.1	40.3	3.2	7.2	4.0
Llama-3-SFT	rewarding IFT + Gold RM	37.1	46.8	9.7	9.7	0
Llama-3-8B-it	Prompt with Gold RM	64.0	72.1	8.1	8.1	0
Llama-3-8B-it	Prompt with External ORM	64.0	68.0	4.0	5.9	1.9
Llama-3-8B-it	Intrinsic self-correction	64.0	48.1	-15.9	7.1	23.0
Llama-3-8B-it	STaR/RAFT for self-correctio	76.0	63.1	-12.9	7.9	20.8
Llama-3-8B-it	STaR/RAFT+ for self-correctio	75.7	67.0	-8.7	8.6	17.3
Llama-3-8B-it	Self-rewarding IFT	73.2	78.2	5.0	9.1	4.1
Llama-3-SFT	Prompt with Gold RM	74.6	83.1	8.5	8.5	0
Llama-3-SFT	Prompt with External ORM	74.6	76.7	2.1	5.5	3.4
Llama-3-SFT	Intrinsic self-correction	74.6	67.4	-7.2	7.6	14.8
Llama-3-SFT	STaR/RAFT for self-correctio	73.8	67.4	-6.4	9.0	15.4
Llama-3-SFT	STaR/RAFT+ for self-correctio	73.9	73.5	-0.4	8.6	9.0
Llama-3-SFT	Self-rewarding IFT	76.1	79.2	3.1	4.7	1.6

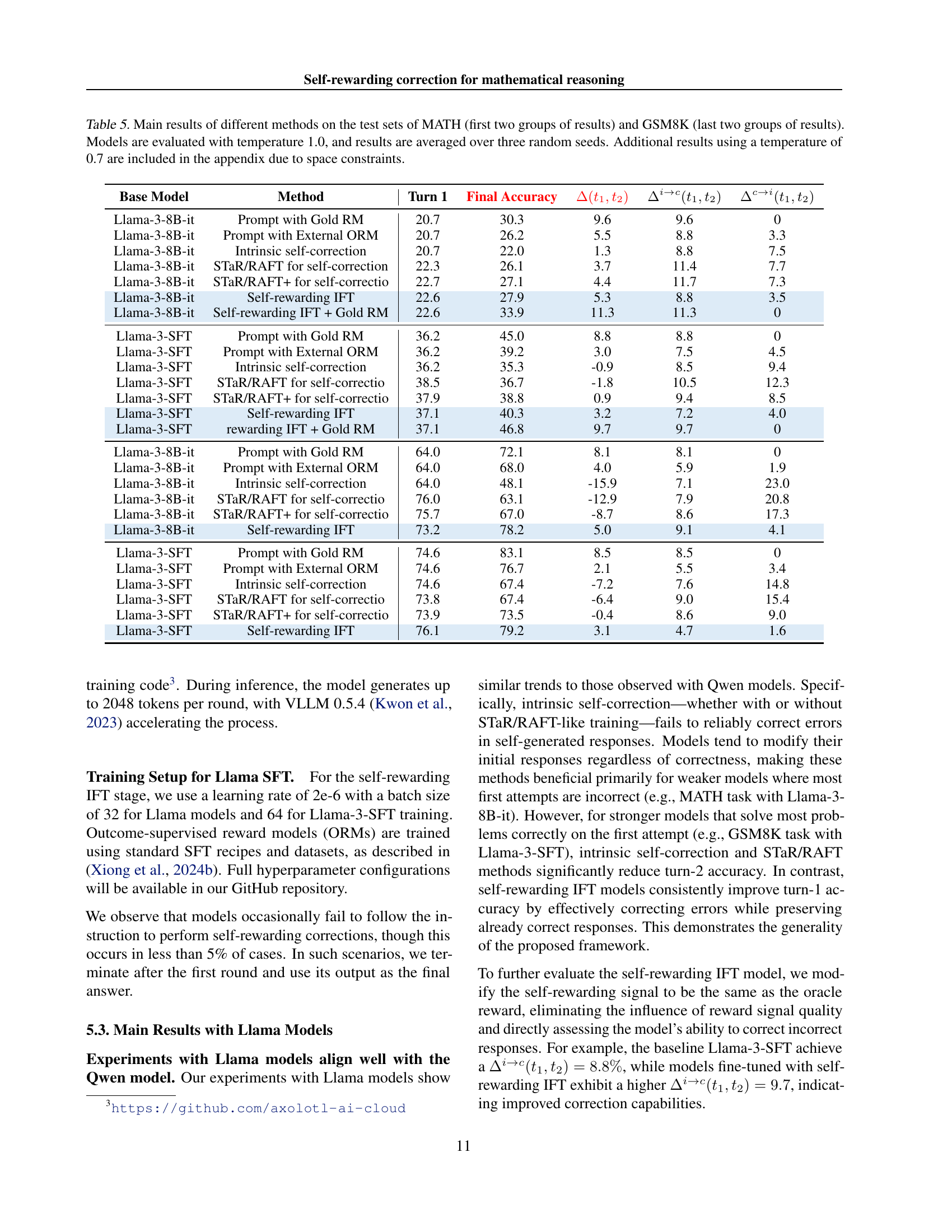
🔼 This table presents the performance comparison of various methods on MATH and GSM8K datasets. The methods include using gold standard reward models, intrinsic self-correction, STaR/RAFT (and its enhanced version), and the proposed self-rewarding IFT approach. Performance is evaluated based on turn 1 accuracy, final accuracy, the improvement in accuracy from turn 1 to the final answer, the fraction of problems correctly solved after correction, and the fraction of problems incorrectly solved after correction. The results are averaged across three different random seeds, and the models are evaluated with a temperature setting of 1.0. Due to space limitations, additional results using a temperature of 0.7 are included in the appendix.
read the caption
Table 5: Main results of different methods on the test sets of MATH (first two groups of results) and GSM8K (last two groups of results). Models are evaluated with temperature 1.0, and results are averaged over three random seeds. Additional results using a temperature of 0.7 are included in the appendix due to space constraints.

Method	Turn 1	Final Accuracy	$\Delta(t_{1},t_{2})$	$\Delta^{i\to c}(t_{1},t_{2})$	$\Delta^{c\to i}(t_{1},t_{2})$	MATH C	MATH W
Llama-3-SFT + Gold RM	36.2	45.0	8.8	8.8	0	100	100
Llama-3-SFT + External ORM	36.2	39.2	3.0	7.5	4.5	66.9	88.4
Llama-3-SFT + Self-rewarding RM	36.2	38.9	2.7	7.4	4.7	67.0	86.7
Self-rewarding IFT + Self-rewarding RM	37.1	40.3	3.2	7.2	4.0	70.0	76.4
Self-rewarding IFT + Gold RM	37.1	46.8	9.7	9.7	0	100	100

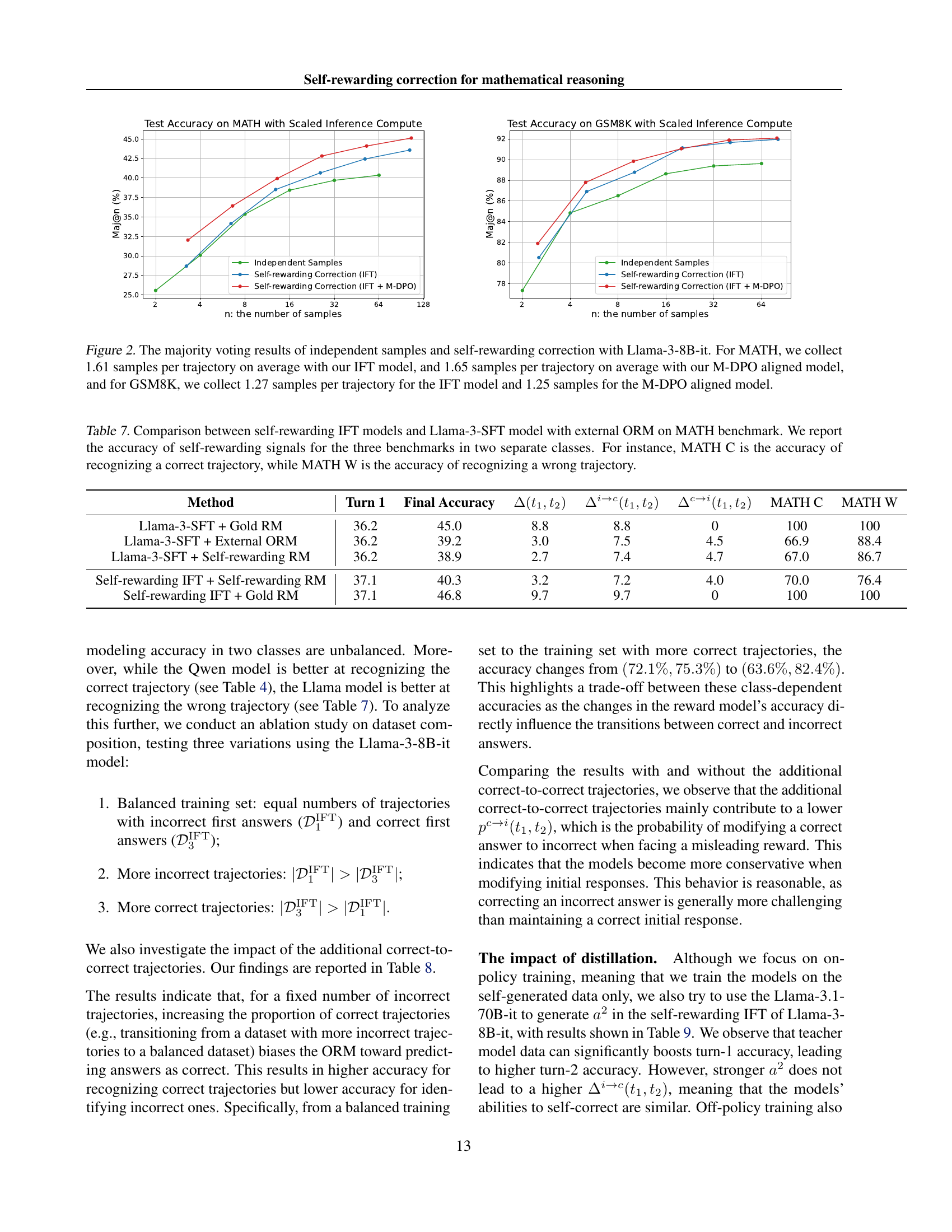
🔼 This table compares the performance of self-rewarding Instruction Following fine-tuning (IFT) models against Llama-3-SFT models using an external Oracle Reward Model (ORM) on the MATH benchmark. It evaluates the accuracy of the models in recognizing correct and incorrect reasoning trajectories. The accuracy is broken down into two classes for each benchmark: ‘C’ representing the accuracy of identifying correct trajectories, and ‘W’ representing the accuracy of identifying incorrect trajectories. The table shows the Turn 1 accuracy, final accuracy, change in accuracy from turn 1 to final answer, fraction of problems changing from incorrect to correct and vice versa, and the reward model accuracy for each method.
read the caption
Table 7: Comparison between self-rewarding IFT models and Llama-3-SFT model with external ORM on MATH benchmark. We report the accuracy of self-rewarding signals for the three benchmarks in two separate classes. For instance, MATH C is the accuracy of recognizing a correct trajectory, while MATH W is the accuracy of recognizing a wrong trajectory.

Method	Turn 1	Final Accuracy	$\Delta(t_{1},t_{2})$	$\Delta^{i\to c}(t_{1},t_{2})$	$\Delta^{c\to i}(t_{1},t_{2})$	$p^{c\to i}(t_{1},t_{2})$	RM Accuracy
Llama-3-SFT + Gold RM	36.2	45.0	8.8	8.8	0	-	(100, 100)
Llama-3-SFT + External ORM $(\star)$	36.2	39.2	3.0	7.5	4.5	37.6	(66.9, 88.4)
Llama-3-SFT + Self-rewarding RM $(\star)$	36.2	38.9	2.7	7.4	4.7	39.4	(67.0, 86.7)
Self-rewarding IFT + Balanced $(\star)$	37.4	40.1	2.7	7.4	4.7	45.0	(72.1, 75.3)
+ c2c 60K	37.1	40.3	3.2	7.2	4.0	36.1	(70.0, 76.4)
+ Gold RM	37.1	46.8	9.7	9.7	0	-	(100, 100)
Self-rewarding IFT + More Incorrect	38.1	40.3	2.2	8.0	5.8	41.7	(63.6, 82.4)
+ c2c 60K	37.7	40.8	3.1	8.0	4.7	33.0	(61.5, 84.3)
+ Gold RM	37.7	46.9	9.2	9.2	0	-	(100, 100)
Self-rewarding IFT + More Correct	37.8	40.5	2.7	7.4	4.7	45.2	(72.6, 75.1)
+ c2c 60K	37.9	40.8	2.9	6.6	3.7	35.2	(72.1, 76.2)
+ Gold RM	37.9	47.5	9.6	9.6	0	-	(100, 100)

🔼 This table presents an ablation study on the training data used for self-rewarding instruction following (IFT) with Llama-3-8B-SFT as the base model. It explores the impact of varying the proportions of trajectories with correct and incorrect initial responses in the training data. Three data configurations are compared: a balanced set, one with more incorrect trajectories, and one with more correct trajectories. For each configuration, results are shown for the self-rewarding IFT model, along with variants including additional correct-to-correct trajectories and replacing self-rewarding signals with ground truth labels during inference. The results allow for analyzing the influence of data composition on the model’s performance and ability to self-correct.
read the caption
Table 8: Ablation study on the training sets of self-rewarding IFT with the base model Llama-3-8B-SFT. For the balanced training set, we use 125K trajectories with incorrect first answers (𝒟1IFTsubscriptsuperscript𝒟IFT1\mathcal{D}^{\mathrm{IFT}}_{1}caligraphic_D start_POSTSUPERSCRIPT roman_IFT end_POSTSUPERSCRIPT start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT) and 125K with correct first answers (𝒟3IFTsubscriptsuperscript𝒟IFT3\mathcal{D}^{\mathrm{IFT}}_{3}caligraphic_D start_POSTSUPERSCRIPT roman_IFT end_POSTSUPERSCRIPT start_POSTSUBSCRIPT 3 end_POSTSUBSCRIPT). For sets with more incorrect trajectories, |𝒟1IFT|=125⁢Ksubscriptsuperscript𝒟IFT1125𝐾|\mathcal{D}^{\mathrm{IFT}}_{1}|=125K| caligraphic_D start_POSTSUPERSCRIPT roman_IFT end_POSTSUPERSCRIPT start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT | = 125 italic_K and |𝒟3IFT|=60⁢Ksubscriptsuperscript𝒟IFT360𝐾|\mathcal{D}^{\mathrm{IFT}}_{3}|=60K| caligraphic_D start_POSTSUPERSCRIPT roman_IFT end_POSTSUPERSCRIPT start_POSTSUBSCRIPT 3 end_POSTSUBSCRIPT | = 60 italic_K. Finally, for the training set with more correct trajectories, we have |𝒟1IFT|=125⁢Ksubscriptsuperscript𝒟IFT1125𝐾|\mathcal{D}^{\mathrm{IFT}}_{1}|=125K| caligraphic_D start_POSTSUPERSCRIPT roman_IFT end_POSTSUPERSCRIPT start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT | = 125 italic_K and |𝒟3IFT|=180⁢Ksubscriptsuperscript𝒟IFT3180𝐾|\mathcal{D}^{\mathrm{IFT}}_{3}|=180K| caligraphic_D start_POSTSUPERSCRIPT roman_IFT end_POSTSUPERSCRIPT start_POSTSUBSCRIPT 3 end_POSTSUBSCRIPT | = 180 italic_K. Models trained with more incorrect trajectories (marked by (⋆)⋆(\star)( ⋆ )) are used as final model and the dataset is also used to train the external ORM. “+ c2c 60K” indicates an additional 60K correct-to-correct trajectories and “+Gold RM” replaces self-rewarding signals with ground-truth labels during inference.

Method	Turn 1	Final Accuracy	$\Delta(t_{1},t_{2})$	$\Delta^{i\to c}(t_{1},t_{2})$	$\Delta^{c\to i}(t_{1},t_{2})$	$p^{c\to i}(t_{1},t_{2})$	Accuracy
Self-rewarding IFT (MATH)	22.6	27.9	5.3	8.8	3.5	43.9	(63.6, 76.1)
+ M-DPO with $\mathcal{D}_{1}$	24.9	29.1	4.2	9.3	5.1	50.3	(59.2, 77.1)
+ M-DPO with $\mathcal{D}_{2}$	24.2	27.8	3.6	5.5	1.9	31.3	(74.7, 65.8)
+ M-DPO with $\mathcal{D}_{1,2}$	23.9	28.6	4.7	6.5	1.8	27.5	(73.4, 68.6)
+ M-DPO with $\mathcal{D}_{1,2,3}$ (well-tuned)	23.3	29.9	6.6	9.4	2.8	34.2	(61.6, 81.4)
Self-rewarding IFT + Distillation (MATH)	28.3	30.5	2.2	8.0	5.8	37.5	(36.7, 76.7)
Self-rewarding IFT (GSM8K)	73.2	78.2	5.0	9.1	4.1	26.3	(79.3, 74.0)
+ M-DPO with $\mathcal{D}_{1}$	75.3	79.1	3.8	8.1	4.3	31.1	(82.1, 70.1)
+ M-DPO with $\mathcal{D}_{2}$	74.6	79.9	5.3	7.1	1.8	12.5	(80.3, 70.4)
+ M-DPO with $\mathcal{D}_{1,2}$	74.6	81.0	6.4	8.9	2.5	18.8	(82.3, 69.6)
+ M-DPO with $\mathcal{D}_{1,2,3}$	74.9	80.7	5.8	8.6	2.8	15.8	(76.7, 67.1)

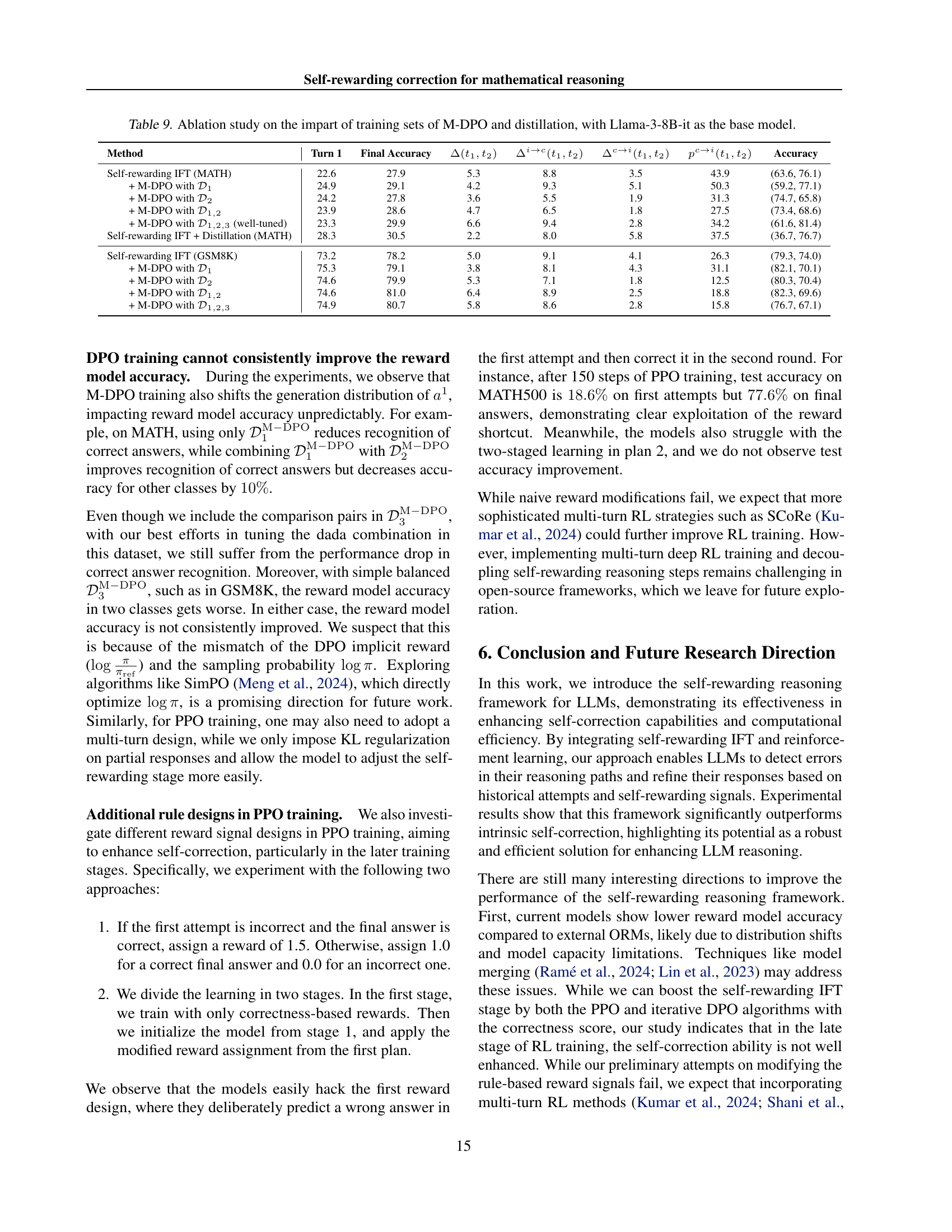
🔼 This table presents the ablation study on the impact of training data and distillation techniques on the performance of a mathematical reasoning model. It uses Llama-3-8B-it as the base model and explores different configurations: standard self-rewarding IFT, M-DPO with various data distributions (D1, D2, D1&2, D1&2&3), and the inclusion of distillation. For each configuration, the table shows turn 1 accuracy, final accuracy, the improvement in accuracy between turn 1 and the final answer, the percentage of problems correctly solved after correction, the percentage of problems incorrectly solved after correction, and reward model accuracy for both correct and incorrect trajectories. This comprehensive analysis allows for a detailed assessment of the effect of data composition and distillation on both the overall accuracy and the model’s ability to self-correct.
read the caption
Table 9: Ablation study on the impart of training sets of M-DPO and distillation, with Llama-3-8B-it as the base model.

Base Model	Method	Turn 1	Final Accuracy	$\Delta(t_{1},t_{2})$	$\Delta^{i\to c}(t_{1},t_{2})$	$\Delta^{c\to i}(t_{1},t_{2})$
Llama-3-8B-it	Prompt with Gold RM	24.1	33.1	9.0	9.0	0
Llama-3-8B-it	Intrinsic self-correction	24.1	25.6	1.5	10.0	8.5
Llama-3-8B-it	STaR/RAFT for self-correction	25.7	28.0	2.3	10.9	8.6
Llama-3-8B-it	STaR/RAFT+ for self-correction	25.5	28.6	3.1	10.6	7.5
Llama-3-8B-it	Self-correct with External ORM	24.1	29.3	5.2	8.7	3.5
Llama-3-8B-it	Self-rewarding IFT	25.0	29.4	4.4	7.5	3.1
Llama-3-SFT	Prompt with Gold RM	43.1	51.0	7.9	7.9	0
Llama-3-SFT	Intrinsic self-correction	43.0	41.7	-1.3	6.8	8.1
Llama-3-SFT	STaR/RAFT for self-correction	42.5	40.4	-2.1	9.3	11.4
Llama-3-SFT	STaR/RAFT+ for self-correction	42.9	43.1	0.2	8.1	7.9
Llama-3-SFT	Self-correct with External ORM	43.1	44.6	1.5	6.1	4.6
Llama-3-SFT	Self-rewarding IFT	43.1	45.7	2.6	6.7	4.1
Llama-3-8B-it	Prompt with Gold RM	67.5	74.0	6.5	6.5	0
Llama-3-8B-it	Intrinsic self-correction	67.5	51.6	-15.9	6.1	22.0
Llama-3-8B-it	STaR/RAFT for self-correction	77.9	62.5	-15.4	7.9	23.3
Llama-3-8B-it	STaR/RAFT+ for self-correction	78.4	66.9	-11.5	7.4	18.9
Llama-3-8B-it	Self-correct with External ORM	67.5	69.9	2.4	4.5	2.1
Llama-3-8B-it	Self-rewarding IFT	76.4	80.5	4.1	7.7	3.6
Llama-3-SFT	Prompt with Gold RM	81.5	86.6	5.1	5.1	0
Llama-3-SFT	Intrinsic self-correction	81.5	74.8	-6.7	5.3	12.0
Llama-3-SFT	STaR/RAFT for self-correction	78.5	72.7	-5.8	8.6	14.4
Llama-3-SFT	STaR/RAFT+ for self-correction	79.0	78.4	-0.6	6.3	6.9
Llama-3-SFT	Self-correct with External ORM	81.5	82.3	0.9	2.3	1.4
Llama-3-SFT	Self-rewarding IFT	80.8	82.6	1.8	2.7	0.9

🔼 This table presents the performance comparison of various methods on the MATH dataset, focusing on mathematical reasoning capabilities. The results include metrics such as Turn 1 accuracy (accuracy of the initial response), final accuracy (accuracy of the final answer after potential corrections), and changes in accuracy from the first to the final attempt. Different methods are compared including baselines like single-turn models and those utilizing external reward models, along with the proposed self-rewarding and self-correction methods. The test temperature used was 0.7.
read the caption
Table 10: Main results of different methods on the test set of MATH. The test temperature is 0.7.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Self-Reward Intro#

2-Stage Training#

Rejection Sampling#

Llama vs. Qwen#

Future Work#

More visual insights#

Full paper#