TL;DR#
Large Language Models (LLMs) have shown impressive abilities, but struggle with rigorous mathematical reasoning. Determining if a polynomial is non-negative, crucial for optimization, remains a challenge. This paper introduces SoS-1K, a dataset of 1,000 polynomials, with expert-designed instructions based on five increasingly difficult criteria. Evaluating state-of-the-art LLMs reveals poor performance without guidance, hovering near random guessing. LLMs need explicit help to perform this math task.
The study demonstrated that providing high-quality reasoning instructions significantly boosts LLM accuracy. A fine-tuned 7B model, SoS-7B, outperforms much larger models. Findings highlight LLMs’ potential to push mathematical reasoning boundaries and tackle computationally hard (NP-hard) problems. Code is available at the project’s github.
Key Takeaways#
Why does it matter?#
This paper pioneers the use of LLMs in solving complex mathematical problems like determining polynomial non-negativity. It highlights the potential of AI to advance mathematical research and tackle NP-hard problems, paving the way for future advancements. The meticulously curated SoS-1K dataset will serve as a valuable resource for future research.
Visual Insights#

🔼 This figure compares three different prompting methods used to guide large language models (LLMs) in determining whether a given polynomial can be expressed as a sum of squares (SoS). SoS Plain shows a simple question with no additional guidance. SoS Simple provides a structured classification based on simple criteria, while SoS Reasoning offers a detailed, step-by-step approach with progressively challenging criteria and expert-designed reasoning instructions. The figure highlights the increasing level of detail and guidance provided to the LLM, demonstrating how the structured prompts improve the accuracy and reasoning process.
read the caption
Figure 1: Demonstration of SoS Plain (left), SoS Simple (mid), and SoS Reasoning (right).
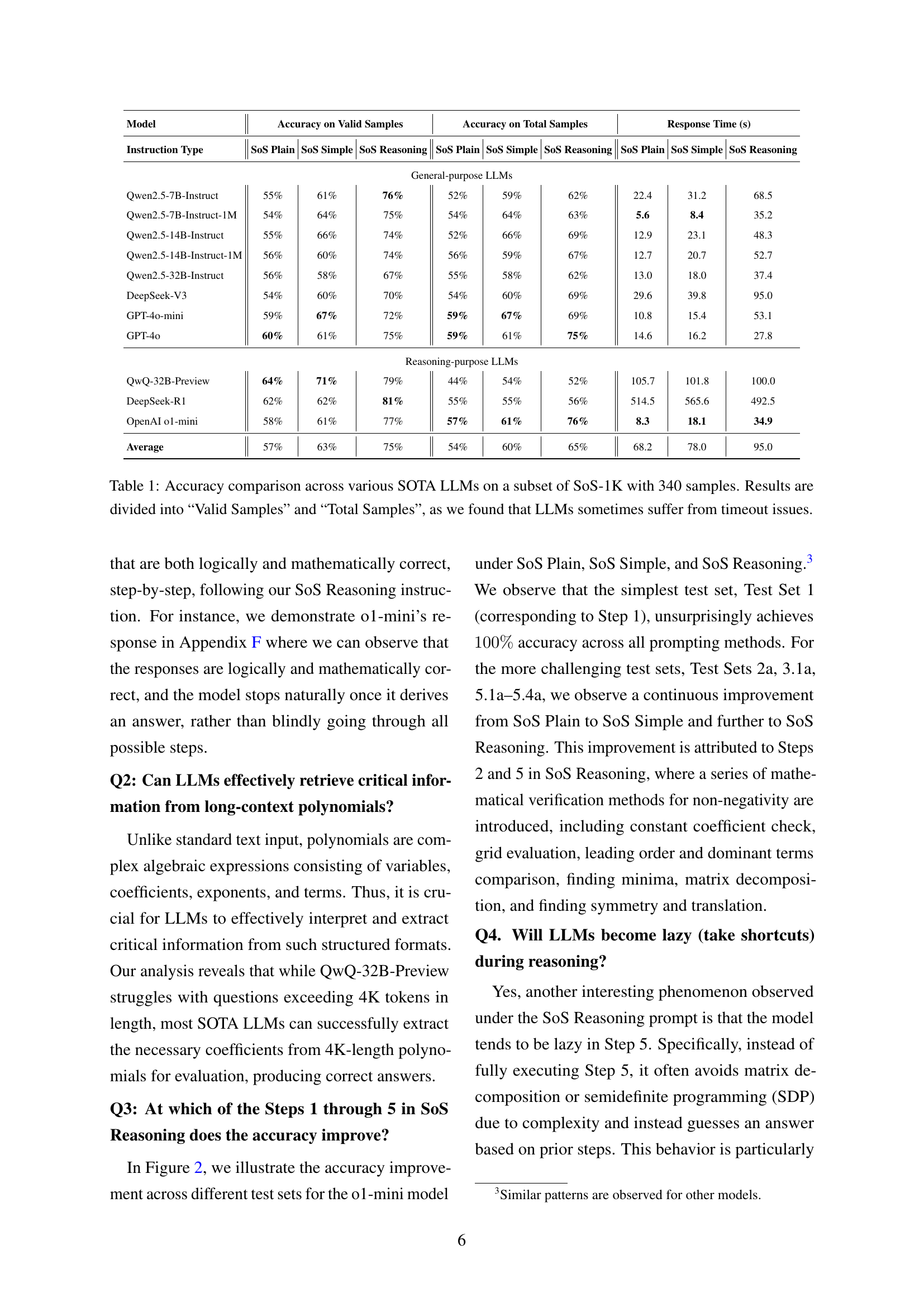
| Model | Accuracy on Valid Samples | Accuracy on Total Samples | Response Time (s) | ||||||
| Instruction Type | SoS Plain | SoS Simple | SoS Reasoning | SoS Plain | SoS Simple | SoS Reasoning | SoS Plain | SoS Simple | SoS Reasoning |
| General-purpose LLMs | |||||||||
| Qwen2.5-7B-Instruct | 55% | 61% | 76% | 52% | 59% | 62% | 22.4 | 31.2 | 68.5 |
| Qwen2.5-7B-Instruct-1M | 54% | 64% | 75% | 54% | 64% | 63% | 5.6 | 8.4 | 35.2 |
| Qwen2.5-14B-Instruct | 55% | 66% | 74% | 52% | 66% | 69% | 12.9 | 23.1 | 48.3 |
| Qwen2.5-14B-Instruct-1M | 56% | 60% | 74% | 56% | 59% | 67% | 12.7 | 20.7 | 52.7 |
| Qwen2.5-32B-Instruct | 56% | 58% | 67% | 55% | 58% | 62% | 13.0 | 18.0 | 37.4 |
| DeepSeek-V3 | 54% | 60% | 70% | 54% | 60% | 69% | 29.6 | 39.8 | 95.0 |
| GPT-4o-mini | 59% | 67% | 72% | 59% | 67% | 69% | 10.8 | 15.4 | 53.1 |
| GPT-4o | 60% | 61% | 75% | 59% | 61% | 75% | 14.6 | 16.2 | 27.8 |
| Reasoning-purpose LLMs | |||||||||
| QwQ-32B-Preview | 64% | 71% | 79% | 44% | 54% | 52% | 105.7 | 101.8 | 100.0 |
| DeepSeek-R1 | 62% | 62% | 81% | 55% | 55% | 56% | 514.5 | 565.6 | 492.5 |
| OpenAI o1-mini | 58% | 61% | 77% | 57% | 61% | 76% | 8.3 | 18.1 | 34.9 |
| Average | 57% | 63% | 75% | 54% | 60% | 65% | 68.2 | 78.0 | 95.0 |
🔼 This table presents a comparison of the accuracy of various state-of-the-art Large Language Models (LLMs) on a subset of the SoS-1K dataset. The SoS-1K dataset contains approximately 1000 polynomials, and the subset used here contains 340 randomly selected polynomials. The accuracy is evaluated using three different prompting methods (SoS Plain, SoS Simple, and SoS Reasoning), which provide progressively more structured guidance to the LLMs. The table shows the accuracy achieved by each LLM on both valid samples (where the LLM produced a response within the time limit) and total samples. The results reveal the performance difference between general-purpose and reasoning-focused LLMs, highlighting the impact of instruction quality on LLM accuracy for this type of complex mathematical reasoning problem.
read the caption
Table 1: Accuracy comparison across various SOTA LLMs on a subset of SoS-1K with 340 samples. Results are divided into “Valid Samples” and “Total Samples”, as we found that LLMs sometimes suffer from timeout issues.
In-depth insights#
SoS1: O1-R1 LLMs#
The paper introduces SoS-1K, a novel dataset designed to evaluate the mathematical reasoning capabilities of Large Language Models (LLMs) specifically in the domain of sum-of-squares (SoS) problems. It investigates whether LLMs can determine if a given multivariate polynomial is nonnegative, a computationally intractable problem with applications in various fields. The research further explores whether the promise of test-time scaling can extend to research-level mathematics, an area largely unexplored. It is designed to probe the capacity of LLMs like Openai 01 and DeepSeek-R1 to solve large-scale SoS programming problems. This involves a carefully constructed dataset of approximately 1,000 polynomials, accompanied by expert-designed reasoning-guiding instructions based on five progressively challenging criteria and is aimed at pushing mathematical reasoning of LLMs.
NP-Hard SoS-1K#
SoS-1K addresses the NP-hard problem of determining polynomial non-negativity. Directly tackling NP-hard challenges positions LLMs at the forefront of mathematical problem-solving. The implication is LLMs can be used in traditionally intractable optimization problems. The ‘1K’ suggests a dataset scale aiming to stress-test LLMs beyond toy examples, benchmarking their ability in realistic problems. This is because real-world mathematical problems often have an NP-hard structure. The use of SoS offers a structured path through the complexity, guiding the LLMs with a mathematically principled approach. This shows how LLMs can handle a specific class of NP-hard problems, which is the one that is related to sum of squares.
LLMs for SoS?#
The paper investigates the potential of Large Language Models (LLMs) in tackling Sum of Squares (SoS) problems, a computationally challenging area within polynomial optimization closely related to Hilbert’s Seventeenth Problem. The research introduces SoS-1K, a curated dataset of approximately 1,000 polynomials designed to evaluate LLMs’ reasoning abilities. The study reveals that LLMs struggle with SoS problems without explicit, structured guidance, highlighting the importance of high-quality, expert-designed instructions. A key finding is that providing LLMs with detailed reasoning traces significantly improves accuracy, demonstrating their latent capacity for mathematical reasoning when effectively prompted. Furthermore, the research shows that fine-tuning a smaller 7B model on the SoS-1K dataset can outperform much larger models like DeepSeek-V3 and GPT-40-mini in accuracy and computation time, suggesting potential for efficient application of LLMs in mathematical problem-solving.
Reasoning boost#
Reasoning boost in LLMs is pivotal for tackling complex mathematical tasks like determining if a multivariate polynomial is a sum of squares (SoS). The study reveals that without structured guidance, LLMs perform poorly. High-quality reasoning instructions significantly improve accuracy, boosting performance considerably. This suggests LLMs possess underlying knowledge but need structured instructions to retrieve and apply it effectively. Reasoning-focused LLMs generally outperform general-purpose ones, emphasizing the importance of reasoning capabilities. Higher-capacity models require fewer thinking tokens, while lower-capacity models need more reasoning steps to achieve optimal performance. Supervised fine-tuning further enhances accuracy and reduces response times, highlighting the potential of LLMs to push mathematical reasoning boundaries and tackle NP-hard problems.
Future of AI SoS#
The “Future of AI SoS” is ripe with potential, especially considering the advancements highlighted in the paper. AI’s role in Sum-of-Squares (SoS) problem-solving could revolutionize mathematical research, making NP-hard problems more tractable. Future research should focus on enhancing LLMs’ reasoning capabilities further, perhaps by incorporating more structured knowledge or developing specialized architectures. The trend of test-time scaling shows promise, suggesting that LLMs can generate more complex solutions with additional computational resources. Addressing current limitations, such as handling longer polynomials and ensuring the validity of LLM decisions, is crucial. Datasets like SoS-1K serve as valuable benchmarks, but expanding them to encompass even more challenging problems will be essential. The potential for AI to not only solve but also generate new mathematical insights, as demonstrated by Qwen-14B-1M’s NNSoS example, signals a paradigm shift in mathematical exploration. However, ethical considerations regarding AI’s role in mathematical discovery needs careful consideration to ensure credibility.
More visual insights#
More on figures

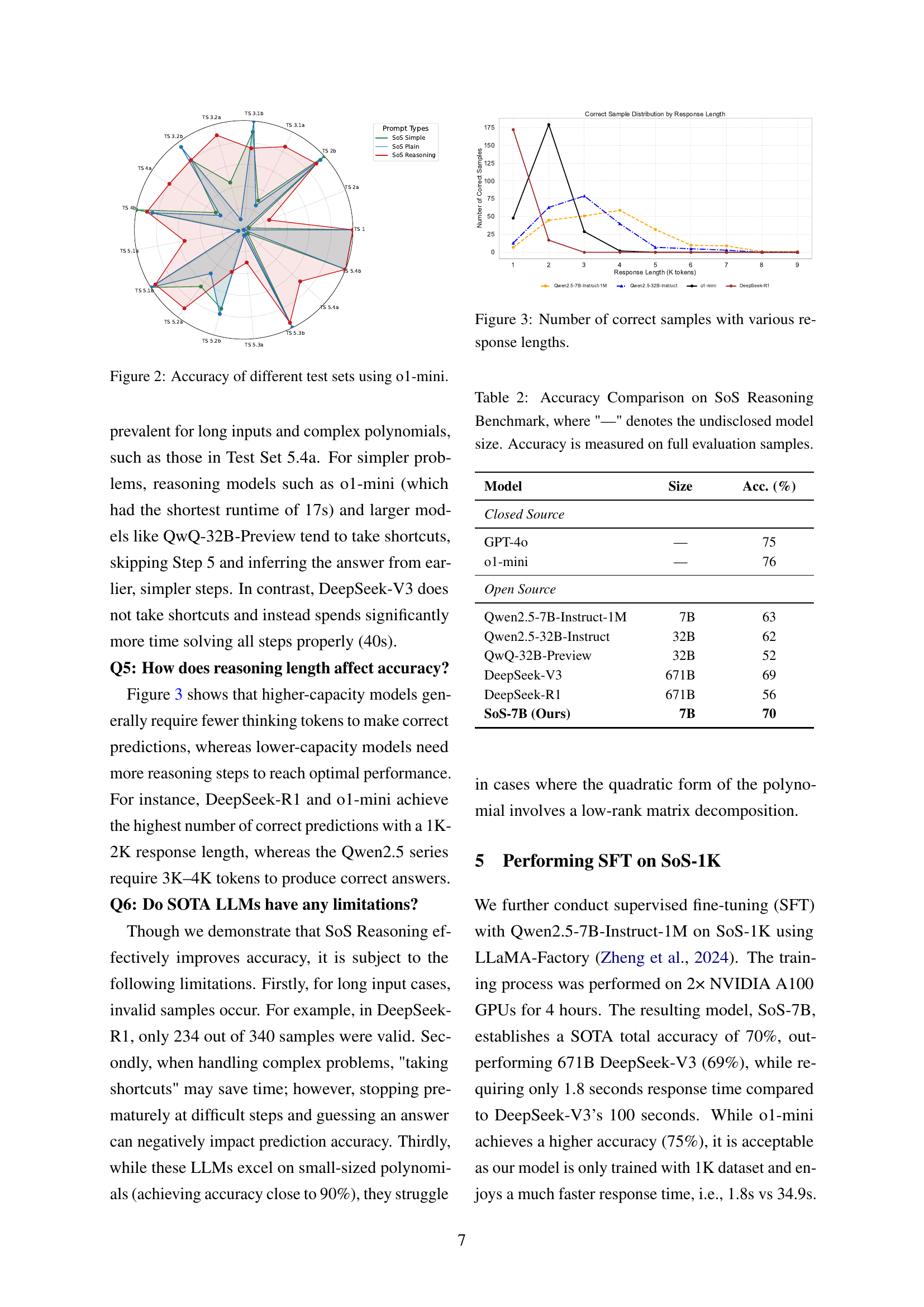
🔼 This figure shows the accuracy of the OpenAI 01-mini language model on various subsets of the SoS-1K dataset, categorized by difficulty. It compares the model’s performance under three different prompting conditions: SoS Plain (a simple question), SoS Simple (with simple instructions), and SoS Reasoning (with detailed, step-by-step instructions). The x-axis represents the test sets and the y-axis represents the accuracy. The figure illustrates how the quality of instructions significantly affects the model’s ability to solve the SoS problem. Each test set has varying degrees of difficulty with some focusing on specific properties of SOS polynomials.
read the caption
Figure 2: Accuracy of different test sets using o1-mini.
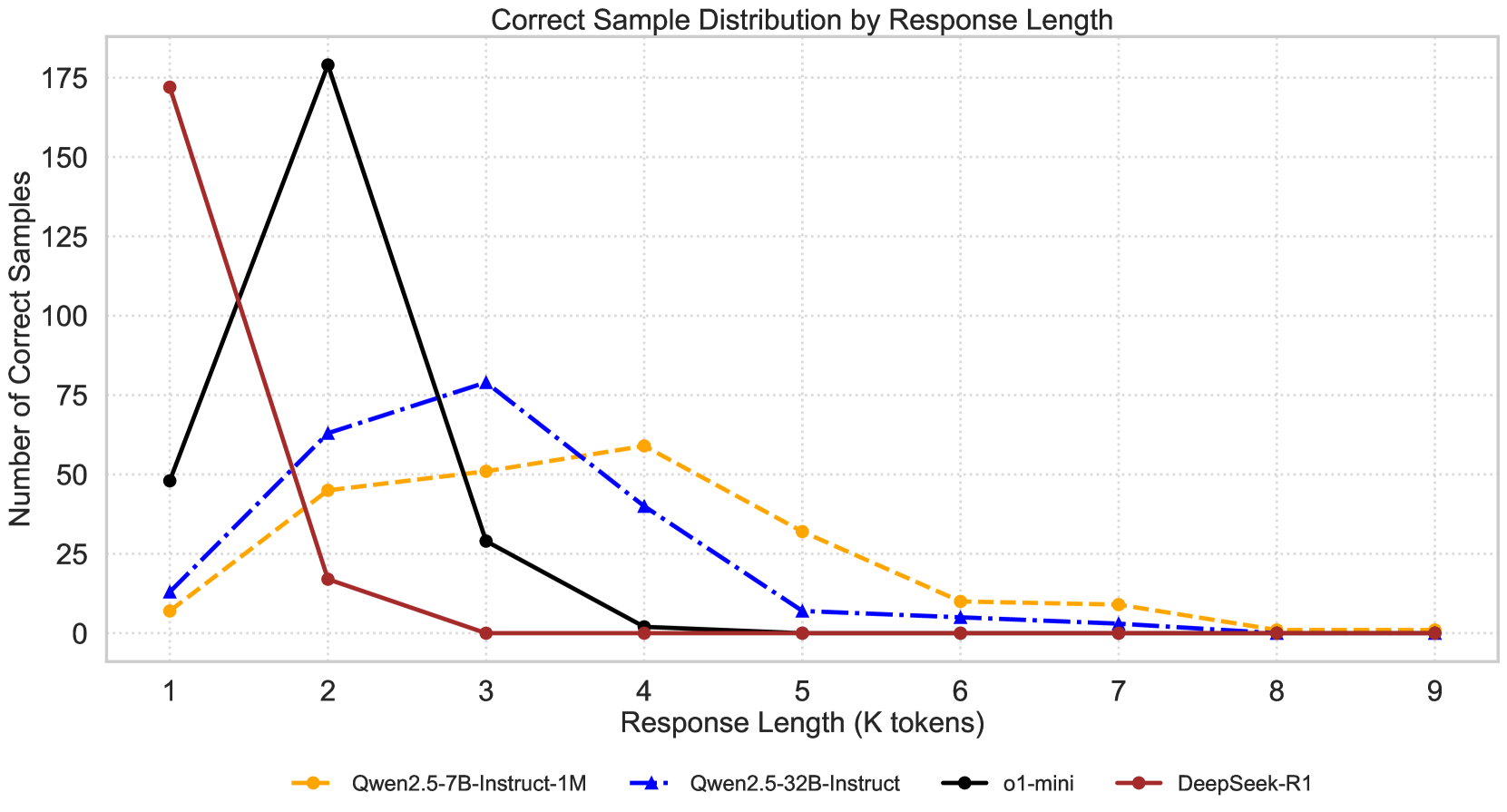
🔼 This figure shows the relationship between the length of the LLMs’ responses (in thousands of tokens) and the number of correct answers they provide for SoS problems. It demonstrates how different models’ performance varies depending on the length of their reasoning processes. For example, some models achieve peak accuracy at a shorter response length, while others require longer reasoning chains to get more correct answers. This illustrates the effect of ’thinking steps’ on accuracy, revealing different capabilities between different models.
read the caption
Figure 3: Number of correct samples with various response lengths.
More on tables
| Model | Size | Acc. (%) |
| Closed Source | ||
| GPT-4o | — | 75 |
| o1-mini | — | 76 |
| Open Source | ||
| Qwen2.5-7B-Instruct-1M | 7B | 63 |
| Qwen2.5-32B-Instruct | 32B | 62 |
| QwQ-32B-Preview | 32B | 52 |
| DeepSeek-V3 | 671B | 69 |
| DeepSeek-R1 | 671B | 56 |
| SoS-7B (Ours) | 7B | 70 |
🔼 This table presents the accuracy of various Large Language Models (LLMs) on the Sum of Squares (SoS) Reasoning benchmark. It compares the performance of both closed-source and open-source models of different sizes, indicating their accuracy in determining whether a given polynomial is an SoS. The accuracy is calculated based on the total number of evaluation samples and not just a subset, providing a comprehensive assessment of model capabilities.
read the caption
Table 2: Accuracy Comparison on SoS Reasoning Benchmark, where '—' denotes the undisclosed model size. Accuracy is measured on full evaluation samples.
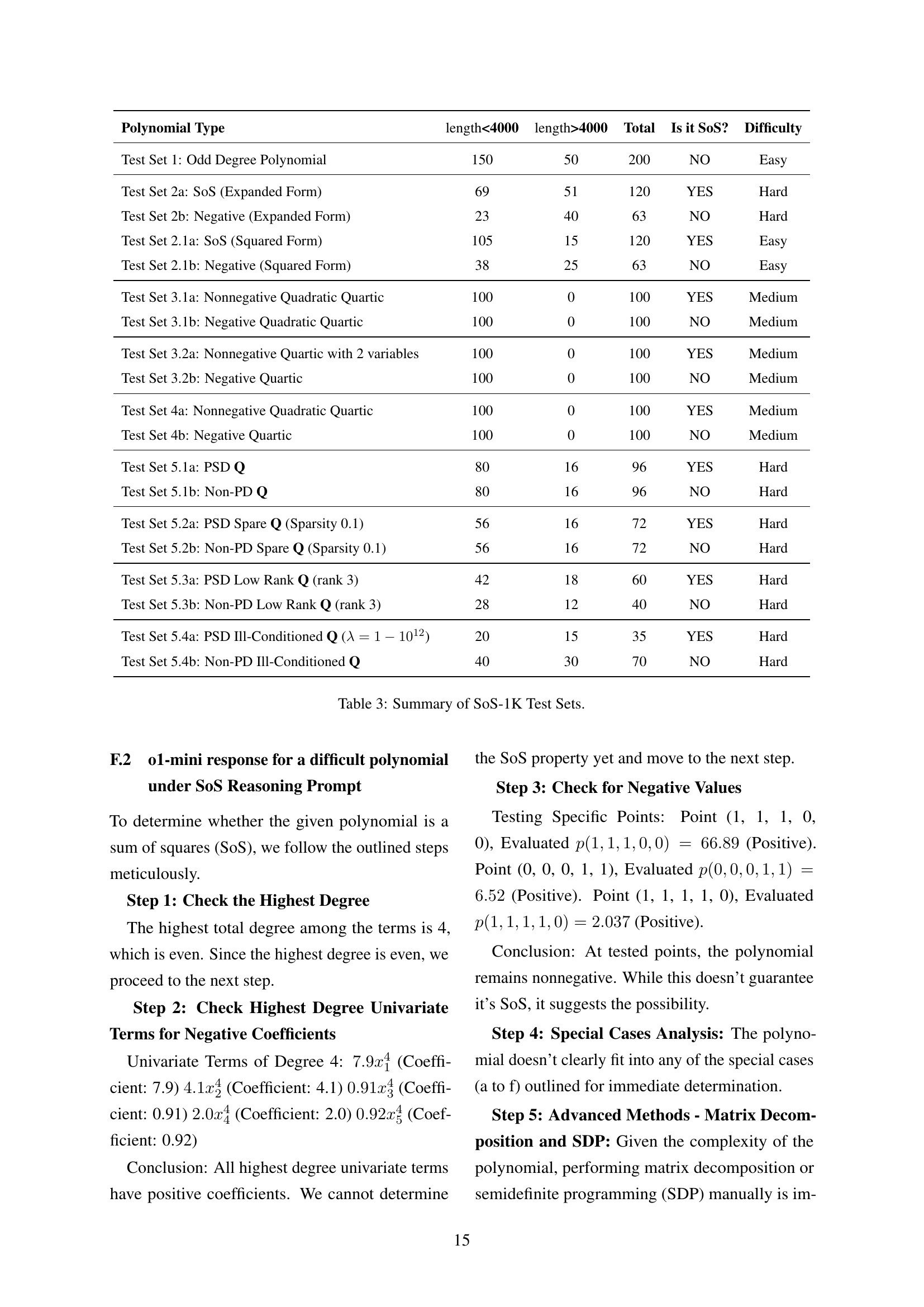
| Polynomial Type | length<4000 | length>4000 | Total | Is it SoS? | Difficulty |
| Test Set 1: Odd Degree Polynomial | 150 | 50 | 200 | NO | Easy |
| Test Set 2a: SoS (Expanded Form) | 69 | 51 | 120 | YES | Hard |
| Test Set 2b: Negative (Expanded Form) | 23 | 40 | 63 | NO | Hard |
| Test Set 2.1a: SoS (Squared Form) | 105 | 15 | 120 | YES | Easy |
| Test Set 2.1b: Negative (Squared Form) | 38 | 25 | 63 | NO | Easy |
| Test Set 3.1a: Nonnegative Quadratic Quartic | 100 | 0 | 100 | YES | Medium |
| Test Set 3.1b: Negative Quadratic Quartic | 100 | 0 | 100 | NO | Medium |
| Test Set 3.2a: Nonnegative Quartic with 2 variables | 100 | 0 | 100 | YES | Medium |
| Test Set 3.2b: Negative Quartic | 100 | 0 | 100 | NO | Medium |
| Test Set 4a: Nonnegative Quadratic Quartic | 100 | 0 | 100 | YES | Medium |
| Test Set 4b: Negative Quartic | 100 | 0 | 100 | NO | Medium |
| Test Set 5.1a: PSD Q | 80 | 16 | 96 | YES | Hard |
| Test Set 5.1b: Non-PD Q | 80 | 16 | 96 | NO | Hard |
| Test Set 5.2a: PSD Spare Q (Sparsity 0.1) | 56 | 16 | 72 | YES | Hard |
| Test Set 5.2b: Non-PD Spare Q (Sparsity 0.1) | 56 | 16 | 72 | NO | Hard |
| Test Set 5.3a: PSD Low Rank Q (rank 3) | 42 | 18 | 60 | YES | Hard |
| Test Set 5.3b: Non-PD Low Rank Q (rank 3) | 28 | 12 | 40 | NO | Hard |
| Test Set 5.4a: PSD Ill-Conditioned Q () | 20 | 15 | 35 | YES | Hard |
| Test Set 5.4b: Non-PD Ill-Conditioned Q | 40 | 30 | 70 | NO | Hard |
🔼 Table 3 provides a summary of the SoS-1K dataset, which consists of approximately 1000 polynomials categorized into different subsets based on characteristics like polynomial degree, presence of specific structures, and difficulty level. Each subset is labeled to indicate whether its polynomials are sums of squares (SoS) or not, and the number of polynomials in each subset. Additionally, the table shows the length distribution of polynomials (less than 4000 characters or more) within each subset and indicates the difficulty level of each subset.
read the caption
Table 3: Summary of SoS-1K Test Sets.
| Model | # Total Samples | # Valid Samples | ||
|---|---|---|---|---|
| Instruction Type | SoS Plain | SoS Simple | SoS Reasoning | |
| DeepSeek-R1 | 340 | 300 | 302 | 234 |
| QWQ-32b | 340 | 233 | 259 | 225 |
| o1-mini | 340 | 338 | 340 | 337 |
| Qwen2.5-7b | 340 | 323 | 332 | 277 |
| GPT-4o | 340 | 336 | 338 | 337 |
| Qwen2.5-7b-1m | 340 | 340 | 339 | 286 |
| Qwen2.5-14b | 340 | 325 | 340 | 316 |
| Qwen2.5-14b-1m | 340 | 340 | 336 | 309 |
| GPT-4o-mini | 340 | 339 | 339 | 327 |
| DeepSeek-V1 | 340 | 340 | 340 | 332 |
| Qwen2.5-32b | 340 | 334 | 339 | 315 |
| Average | 340 | 323 | 328 | 300 |
🔼 This table presents a comparison of the performance of various Large Language Models (LLMs) on a subset of the SoS-1K dataset. For each model, it shows the total number of samples tested, and the number of valid samples (i.e., samples for which the model produced a response within the time limit). The table further breaks down the valid samples according to which prompting method was used (SoS Plain, SoS Simple, and SoS Reasoning). This allows for an assessment of how different prompting strategies impact the accuracy of each model’s predictions regarding the sum-of-squares property of the polynomials.
read the caption
Table 4: # Total Samples and Valid Samples of Different Models.
Full paper#