TL;DR#
Large Language Models (LLMs) face challenges of high computational cost and memory demands due to the Transformer architecture’s quadratic complexity, limiting their use for long sequences. Linear recurrent models offer linear-time training and constant-memory inference, but pretraining them from scratch is costly. Existing linearization methods introduce extra modules that require fine-tuning and overlook gating mechanisms crucial for memory retention in these models.
To address these issues, Liger repurposes pretrained key matrix weights to construct gating mechanisms, creating gated recurrent structures without additional parameters. By fine-tuning these models with Low-Rank Adaptation (LoRA), Liger recovers the performance of original LLMs. The method introduces Liger Attention, a hybrid attention mechanism that improves performance, validated on models from 1B to 8B parameters. The results validate that Liger outperforms other methods.
Key Takeaways#
Why does it matter?#
This paper presents Liger, a novel method for efficiently linearizing LLMs into gated recurrent structures, reducing computational costs, and enabling faster, memory-efficient deployment, opening avenues for practical application in resource-constrained environments and further research into efficient LLM architectures.
Visual Insights#
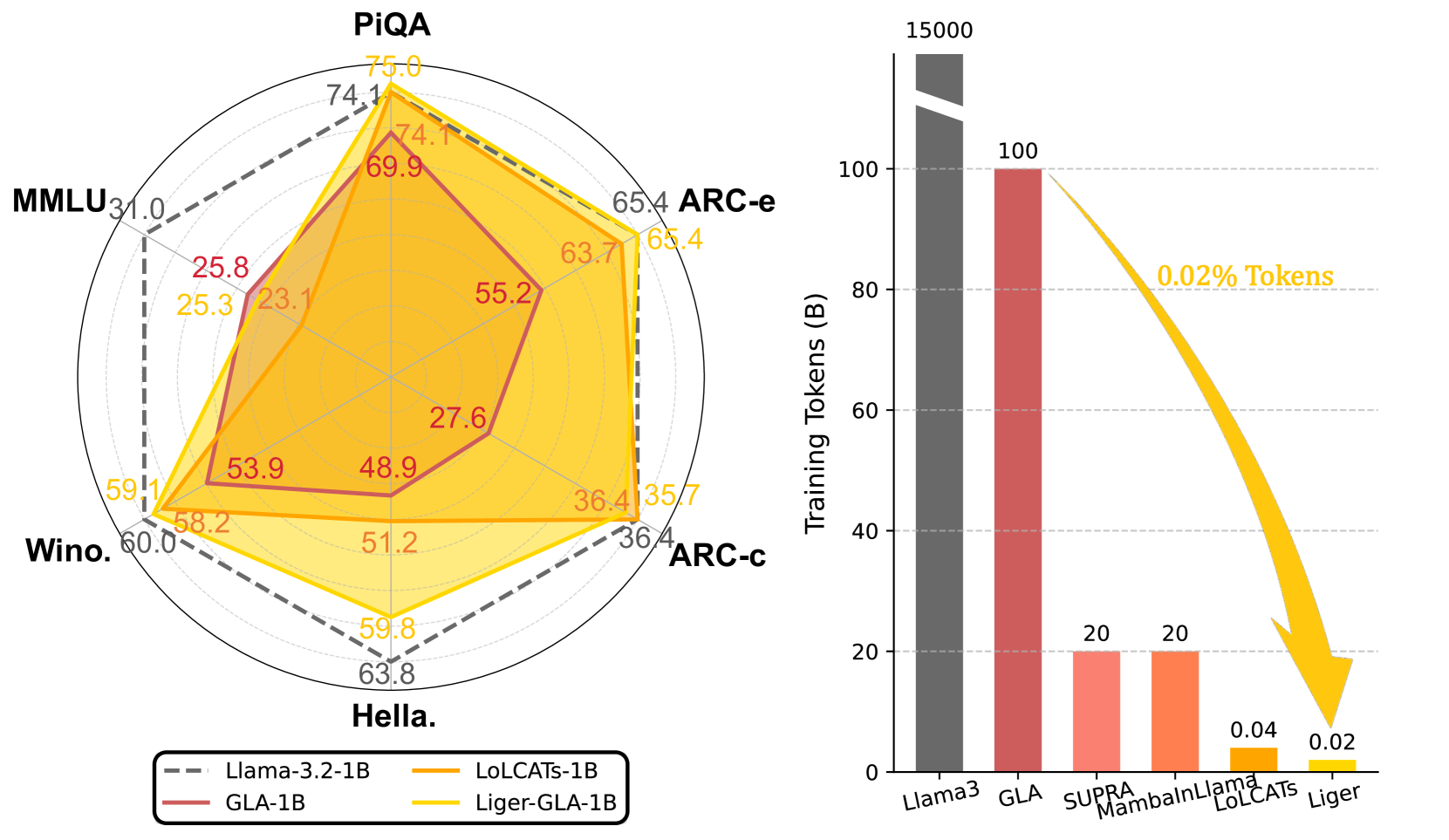
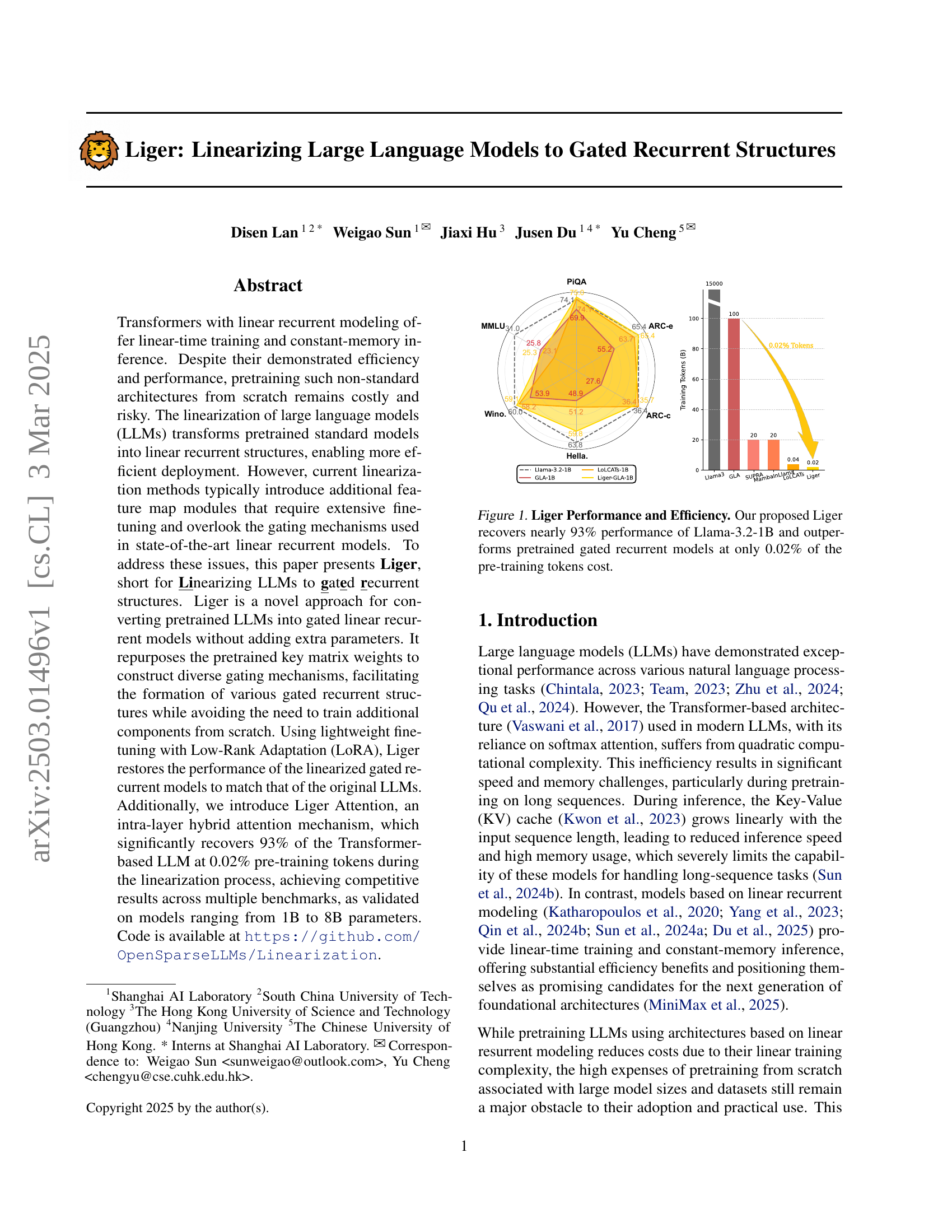
🔼 This figure showcases the performance and efficiency gains achieved by Liger, a novel linearization technique for large language models (LLMs). The left-hand side displays the performance across various benchmarks (PIQA, MMLU, ARC-e, ARC-C, HellaSwag, Winograd Schema Challenge) comparing Liger’s performance to Llama-3.2-1B, a standard Transformer-based model, and other pretrained gated recurrent models. The key observation is that Liger, despite using only 0.02% of the training tokens of Llama-3.2-1B, nearly matches the performance of the original model and significantly outperforms existing gated recurrent models. The right-hand side visually reinforces this finding by showing the performance comparison in terms of training tokens used, highlighting Liger’s exceptional efficiency.
read the caption
Figure 1: Liger Performance and Efficiency. Our proposed Liger recovers nearly 93% performance of Llama-3.2-1B and outperforms pretrained gated recurrent models at only 0.02% of the pre-training tokens cost.
| Model | Gate Parameterization | Pooling for Gate Construction |
| Gated Linear Attention (Yang et al., 2023) | ||
| Mamba2 (Dao & Gu, 2024) | ||
| mLSTM (Beck et al., 2024) | ||
| Gated Retention (Sun et al., 2024c) | ||
| HGRN2 (Qin et al., 2024c) | ||
| RWKV6 (Peng et al., 2024) | ||
| Gated Slot Attention (Zhang et al., 2024c) |
🔼 This table showcases various gated linear recurrent neural network (RNN) architectures and how their gating mechanisms are parameterized. Each row represents a different model (e.g., Gated Linear Attention, Mamba2), detailing the mathematical formula used for its gate (‘Gate Parameterization’). The ‘Pooling for Gate Construction’ column illustrates how a pooling operation is applied to the key projection of pre-trained Large Language Models (LLMs) to efficiently derive the gate parameters, highlighting the reuse of pre-trained weights. This table emphasizes the parameter efficiency of constructing gating mechanisms by leveraging existing pre-trained LLM weights rather than introducing new parameters.
read the caption
Table 1: Gated Linear Recurrent Structures with Variations of Gate 𝐆tsubscript𝐆𝑡\mathbf{G}_{t}bold_G start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT Parameterization. Gating mechanism can be constructed through pooling to reuse the key projection of pre-trained LLM.
In-depth insights#
Gated LM Linearize#
Linearizing gated language models (LMs) is a promising avenue for efficient deployment, trading off some accuracy for significant gains. It allows for the conversion of pre-trained standard models into linear recurrent structures, enabling efficient deployment. However, existing methods can be costly and overlook gating mechanisms used in state-of-the-art linear recurrent models. Introducing gating mechanisms requires a novel approach, such as repurposing weights or integrating intra-layer hybrid attention to maintain the capabilities of pre-trained LLMs while ensuring linear-time inference efficiency.
Key Matrix Gating#
Key matrix gating represents an innovative strategy in model design. It leverages the pre-trained key matrix in transformer models to construct gating mechanisms in linear recurrent structures. This approach has several benefits: it reduces the need for training additional parameters, preserving computational efficiency. Parameter sharing between key projection and gating allows for direct reuse of pre-trained weights, avoiding extra architectural modifications. Careful design is needed to maintain the representational capacity while adapting the architecture. It’s crucial to balance the benefits of linear recurrent structures with maintaining the original transformer’s performance. The gating must effectively regulate information flow within the recurrent structure.
Liger Attention#
Liger Attention proposes an intra-layer hybrid approach, combining Gated Recurrent Modeling (GRM) and Sliding Window Attention (SWA) to leverage the strengths of both. It introduces parameters α and β to control the relative contributions of each attention mechanism which allows for dynamic adjustment based on the specific input and task. By integrating GRM, Liger attention maintains efficient sequence modeling capabilities, while SWA captures local dependencies effectively within a specified window. This hybrid design aims to balance computational efficiency with the ability to model both long-range and short-range dependencies, potentially enhancing performance on various sequence modeling tasks.
LoRA Finetuning#
LoRA (Low-Rank Adaptation) finetuning emerges as a pivotal technique in adapting large language models (LLMs) due to its parameter-efficient nature. This approach strategically freezes the original LLM weights, introducing a smaller set of trainable parameters. By focusing on updating only a subset of the model, LoRA significantly reduces computational costs and memory requirements during the finetuning process. This not only accelerates training but also makes it feasible on resource-constrained environments, democratizing access to LLM customization. The key insight behind LoRA lies in the observation that weight matrices in pre-trained models often have a low intrinsic rank. This allows for approximating weight updates with low-rank matrices, minimizing the number of trainable parameters without substantially compromising performance. Furthermore, LoRA mitigates the risk of overfitting, especially when dealing with limited training data, by preserving the pre-trained knowledge encoded in the original model. The effectiveness of LoRA is evident in its ability to achieve comparable performance to full finetuning while updating significantly fewer parameters.
Hybrid Structure#
A hybrid structure likely refers to combining different architectural elements within a neural network to leverage their respective strengths. This could involve integrating recurrent and feedforward layers, or different types of attention mechanisms. The goal is often to enhance performance, efficiency, or robustness. Combining architectural elements allow it to models that adapt better to diverse data patterns. Careful design is needed to ensure compatibility and avoid bottlenecks, Hybrid model architecture allows it leverage pre-trained weights effectively, and also balances it between model complexity and optimization cost.
More visual insights#
More on figures

🔼 This figure illustrates Liger’s framework, which transforms a Transformer-based large language model (LLM) into a gated linear recurrent structure. It highlights two key steps: (1) replacing the standard softmax attention mechanism with a gated recurrent memory module, which allows for more efficient processing of sequential information and (2) employing Low-Rank Adaptation (LoRA) to fine-tune the resulting Liger architecture, keeping most of the original weights frozen to leverage pre-trained knowledge. The LoRA fine-tuning is lightweight, making the process efficient. This transformation enables efficient chunk-wise parallel training during the training phase and cost-effective linear recurrent inference during the inference phase.
read the caption
Figure 2: Overall Framework of Liger. We linearize the Transformer-based large language model (LLM) architecture into a gated linear recurrent model by 1) Replacing Softmax Attention with a Gated Recurrent Memory module, and 2) Employing LoRA to fine-tune the Liger architecture while frozen most original weight parameters. The Liger architecture enables efficient chunk-wise parallel training also enjoying cheap linear recurrent inference.

🔼 Figure 3 illustrates the hybrid architecture of the Liger model. Liger integrates two types of attention mechanisms: Liger Attention (a novel hybrid mechanism combining gated recurrent modeling and sliding window softmax attention) and standard Transformer attention. The architecture alternates between layers of Liger Transformer blocks, which use the efficient Liger Attention, and standard Transformer blocks, which use traditional softmax attention. This hybrid approach leverages the strengths of both mechanisms – the efficiency of Liger Attention for long sequences and the accuracy of standard Transformer attention – to improve overall model performance. The frequency of standard Transformer block insertion (e.g., every 7 Liger layers) is a hyperparameter that can be tuned. This alternating design is called an ‘inter-hybrid’ architecture because it combines different layer types. The use of Liger Attention within each Liger layer constitutes an ‘intra-hybrid’ architecture.
read the caption
Figure 3: Hybrid Architecture of Liger. Liger adopts intra-hybrid Liger Attention and inter-hybrid model architecture by stacking a layer of standard attention Transformer blocks every a few (e.g. 7) layers of Liger Transformer blocks.

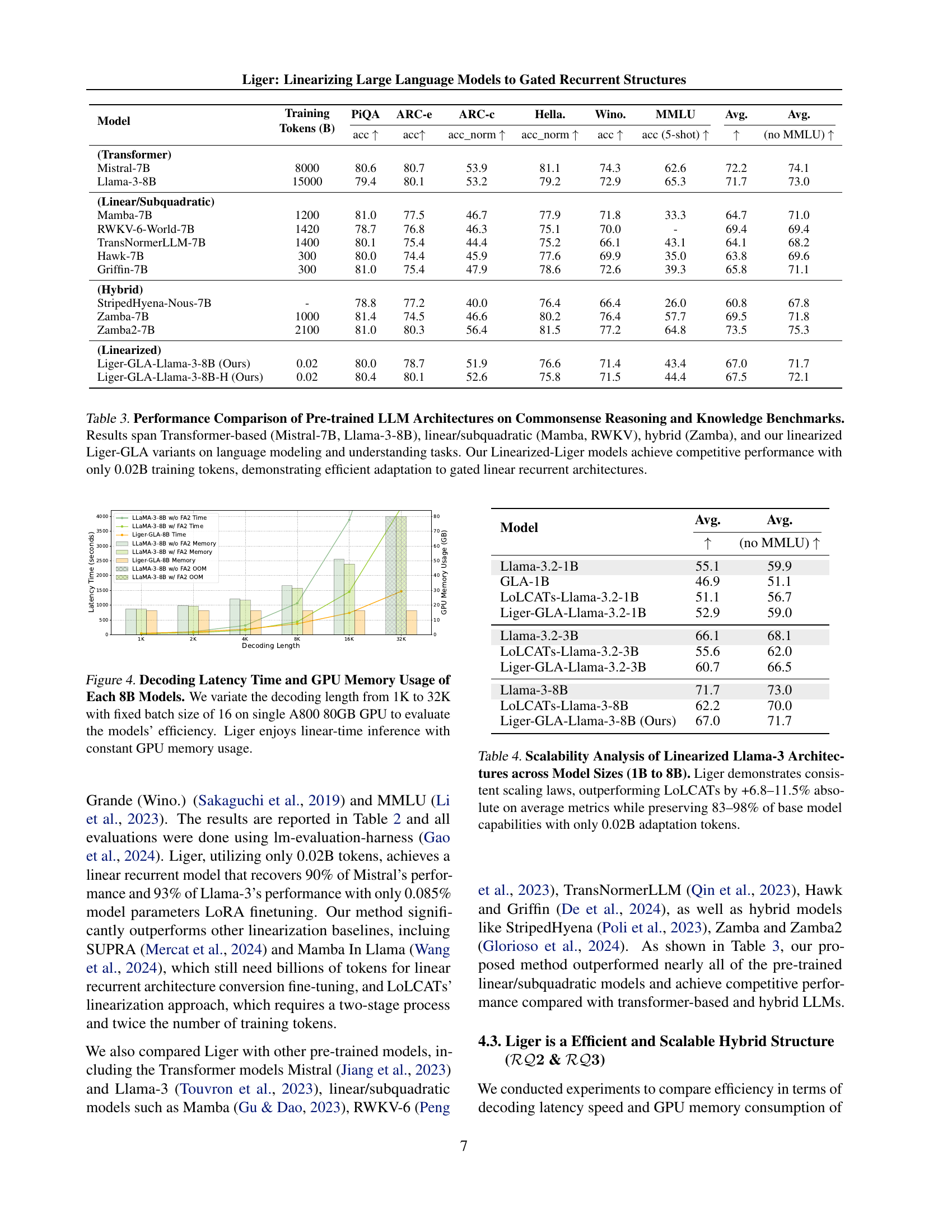
🔼 This figure showcases a comparison of decoding latency and GPU memory usage among three 8B parameter models: Llama-3-8B (without FlashAttention-2), Llama-3-8B (with FlashAttention-2), and Liger-8B. The x-axis represents the decoding sequence length, ranging from 1K to 32K tokens, while the y-axis displays both decoding latency (in seconds) and GPU memory consumption (in GB). A fixed batch size of 16 was used on a single NVIDIA A800 80GB GPU for all experiments. The results highlight that Llama-3-8B, especially with FlashAttention-2, experiences a significant increase in latency and memory usage as the decoding length increases, ultimately resulting in an out-of-memory (OOM) error for the 32K sequence length. In contrast, the Liger-8B model exhibits constant GPU memory usage and linear decoding time, demonstrating its superior efficiency for long sequences.
read the caption
Figure 4: Decoding Latency Time and GPU Memory Usage of Each 8B Models. We variate the decoding length from 1K to 32K with fixed batch size of 16 on single A800 80GB GPU to evaluate the models’ efficiency. Liger enjoys linear-time inference with constant GPU memory usage.
More on tables
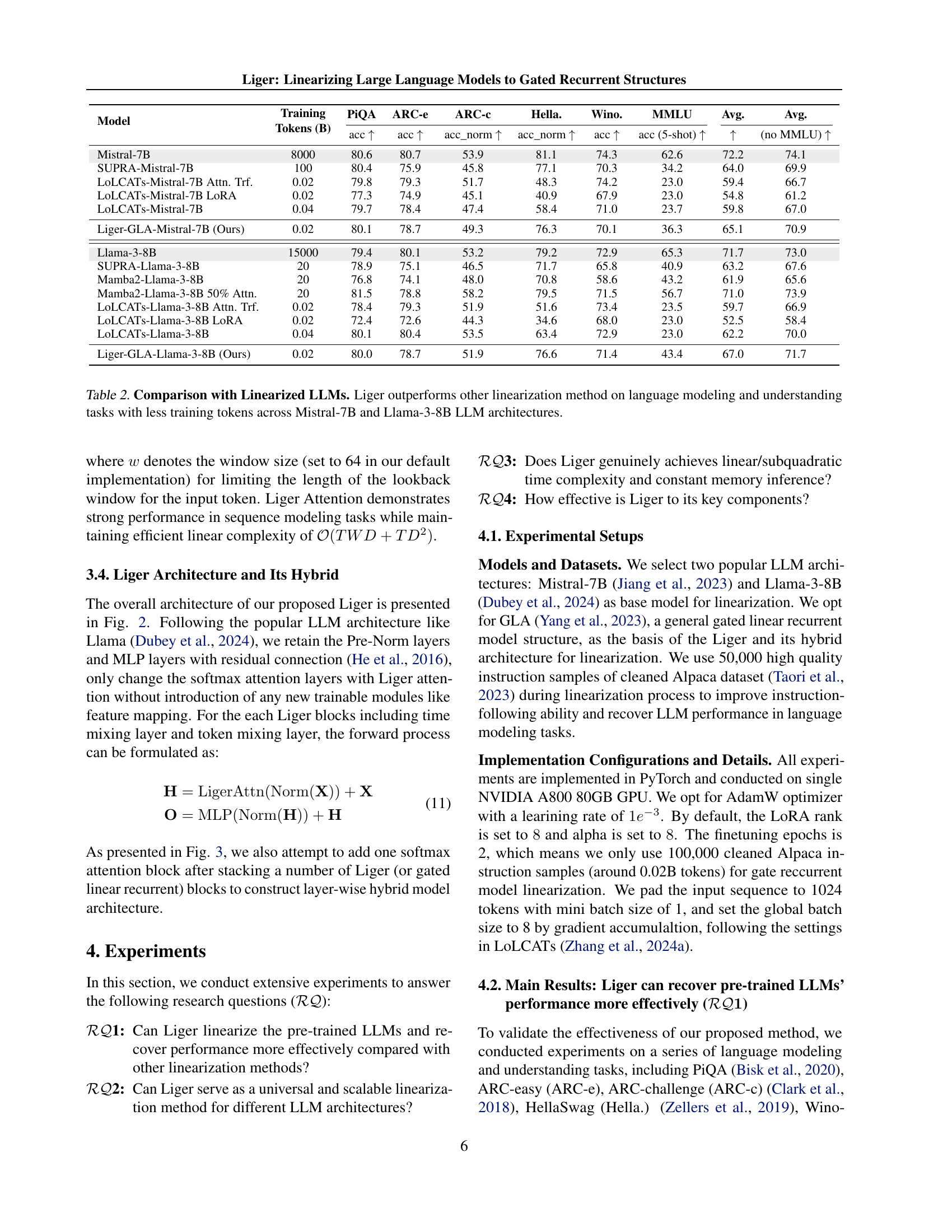
| Model | Training Tokens (B) | PiQA | ARC-e | ARC-c | Hella. | Wino. | MMLU | Avg. | Avg. |
| acc | acc | acc_norm | acc_norm | acc | acc (5-shot) | (no MMLU) | |||
| Mistral-7B | 8000 | 80.6 | 80.7 | 53.9 | 81.1 | 74.3 | 62.6 | 72.2 | 74.1 |
| SUPRA-Mistral-7B | 100 | 80.4 | 75.9 | 45.8 | 77.1 | 70.3 | 34.2 | 64.0 | 69.9 |
| LoLCATs-Mistral-7B Attn. Trf. | 0.02 | 79.8 | 79.3 | 51.7 | 48.3 | 74.2 | 23.0 | 59.4 | 66.7 |
| LoLCATs-Mistral-7B LoRA | 0.02 | 77.3 | 74.9 | 45.1 | 40.9 | 67.9 | 23.0 | 54.8 | 61.2 |
| LoLCATs-Mistral-7B | 0.04 | 79.7 | 78.4 | 47.4 | 58.4 | 71.0 | 23.7 | 59.8 | 67.0 |
| Liger-GLA-Mistral-7B (Ours) | 0.02 | 80.1 | 78.7 | 49.3 | 76.3 | 70.1 | 36.3 | 65.1 | 70.9 |
| Llama-3-8B | 15000 | 79.4 | 80.1 | 53.2 | 79.2 | 72.9 | 65.3 | 71.7 | 73.0 |
| SUPRA-Llama-3-8B | 20 | 78.9 | 75.1 | 46.5 | 71.7 | 65.8 | 40.9 | 63.2 | 67.6 |
| Mamba2-Llama-3-8B | 20 | 76.8 | 74.1 | 48.0 | 70.8 | 58.6 | 43.2 | 61.9 | 65.6 |
| Mamba2-Llama-3-8B 50% Attn. | 20 | 81.5 | 78.8 | 58.2 | 79.5 | 71.5 | 56.7 | 71.0 | 73.9 |
| LoLCATs-Llama-3-8B Attn. Trf. | 0.02 | 78.4 | 79.3 | 51.9 | 51.6 | 73.4 | 23.5 | 59.7 | 66.9 |
| LoLCATs-Llama-3-8B LoRA | 0.02 | 72.4 | 72.6 | 44.3 | 34.6 | 68.0 | 23.0 | 52.5 | 58.4 |
| LoLCATs-Llama-3-8B | 0.04 | 80.1 | 80.4 | 53.5 | 63.4 | 72.9 | 23.0 | 62.2 | 70.0 |
| Liger-GLA-Llama-3-8B (Ours) | 0.02 | 80.0 | 78.7 | 51.9 | 76.6 | 71.4 | 43.4 | 67.0 | 71.7 |
🔼 This table compares the performance of Liger against other LLM linearization methods (SUPRA, LoLCATs, Mamba2) on various downstream tasks (PIQA, ARC-e, ARC-C, HellaSwag, Winogrande, MMLU). It shows that Liger achieves competitive or better results using significantly fewer training tokens (0.02B) for both Mistral-7B and Llama-3-8B base LLMs. This demonstrates Liger’s superior efficiency in converting pretrained LLMs into efficient linear recurrent models while maintaining high performance.
read the caption
Table 2: Comparison with Linearized LLMs. Liger outperforms other linearization method on language modeling and understanding tasks with less training tokens across Mistral-7B and Llama-3-8B LLM architectures.
| Model | Training Tokens (B) | PiQA | ARC-e | ARC-c | Hella. | Wino. | MMLU | Avg. | Avg. |
| acc | acc | acc_norm | acc_norm | acc | acc (5-shot) | (no MMLU) | |||
| (Transformer) | |||||||||
| Mistral-7B | 8000 | 80.6 | 80.7 | 53.9 | 81.1 | 74.3 | 62.6 | 72.2 | 74.1 |
| Llama-3-8B | 15000 | 79.4 | 80.1 | 53.2 | 79.2 | 72.9 | 65.3 | 71.7 | 73.0 |
| (Linear/Subquadratic) | |||||||||
| Mamba-7B | 1200 | 81.0 | 77.5 | 46.7 | 77.9 | 71.8 | 33.3 | 64.7 | 71.0 |
| RWKV-6-World-7B | 1420 | 78.7 | 76.8 | 46.3 | 75.1 | 70.0 | - | 69.4 | 69.4 |
| TransNormerLLM-7B | 1400 | 80.1 | 75.4 | 44.4 | 75.2 | 66.1 | 43.1 | 64.1 | 68.2 |
| Hawk-7B | 300 | 80.0 | 74.4 | 45.9 | 77.6 | 69.9 | 35.0 | 63.8 | 69.6 |
| Griffin-7B | 300 | 81.0 | 75.4 | 47.9 | 78.6 | 72.6 | 39.3 | 65.8 | 71.1 |
| (Hybrid) | |||||||||
| StripedHyena-Nous-7B | - | 78.8 | 77.2 | 40.0 | 76.4 | 66.4 | 26.0 | 60.8 | 67.8 |
| Zamba-7B | 1000 | 81.4 | 74.5 | 46.6 | 80.2 | 76.4 | 57.7 | 69.5 | 71.8 |
| Zamba2-7B | 2100 | 81.0 | 80.3 | 56.4 | 81.5 | 77.2 | 64.8 | 73.5 | 75.3 |
| (Linearized) | |||||||||
| Liger-GLA-Llama-3-8B (Ours) | 0.02 | 80.0 | 78.7 | 51.9 | 76.6 | 71.4 | 43.4 | 67.0 | 71.7 |
| Liger-GLA-Llama-3-8B-H (Ours) | 0.02 | 80.4 | 80.1 | 52.6 | 75.8 | 71.5 | 44.4 | 67.5 | 72.1 |
🔼 Table 3 presents a comprehensive comparison of various large language model (LLM) architectures’ performance across multiple benchmarks focusing on commonsense reasoning and knowledge. It includes results for Transformer-based models (Mistral-7B, Llama-3-8B), linear/subquadratic models (Mamba, RWKV), hybrid models (Zamba), and the proposed Liger-GLA models. The table highlights the competitive performance achieved by the Liger-GLA models, which used only 0.02 billion training tokens. This demonstrates the efficiency of Liger in adapting pre-trained LLMs to gated linear recurrent architectures while maintaining strong performance on various language modeling and understanding tasks.
read the caption
Table 3: Performance Comparison of Pre-trained LLM Architectures on Commonsense Reasoning and Knowledge Benchmarks. Results span Transformer-based (Mistral-7B, Llama-3-8B), linear/subquadratic (Mamba, RWKV), hybrid (Zamba), and our linearized Liger-GLA variants on language modeling and understanding tasks. Our Linearized-Liger models achieve competitive performance with only 0.02B training tokens, demonstrating efficient adaptation to gated linear recurrent architectures.
| Model | Avg. | Avg. |
| (no MMLU) | ||
| Llama-3.2-1B | 55.1 | 59.9 |
| GLA-1B | 46.9 | 51.1 |
| LoLCATs-Llama-3.2-1B | 51.1 | 56.7 |
| Liger-GLA-Llama-3.2-1B | 52.9 | 59.0 |
| Llama-3.2-3B | 66.1 | 68.1 |
| LoLCATs-Llama-3.2-3B | 55.6 | 62.0 |
| Liger-GLA-Llama-3.2-3B | 60.7 | 66.5 |
| Llama-3-8B | 71.7 | 73.0 |
| LoLCATs-Llama-3-8B | 62.2 | 70.0 |
| Liger-GLA-Llama-3-8B (Ours) | 67.0 | 71.7 |
🔼 This table presents a scalability analysis of the Liger model applied to different sizes of Llama-3 (1B, 3B, and 8B parameters). It compares the performance of Liger against vanilla Llama-3, LoLCATs (another linearization method), and GLA (Gated Linear Attention). The key metrics used are accuracy across various downstream tasks (PIQA, ARC-e, ARC-c, HellaSwag, Winograd Schema Challenge, and MMLU). The table highlights Liger’s consistent performance improvements over LoLCATs across different model sizes, with gains ranging from +6.8% to +11.5% on average metrics. Importantly, it shows that Liger achieves this improvement while using significantly fewer training tokens (only 0.02B) and maintaining a high percentage (83-98%) of the original Llama-3 performance.
read the caption
Table 4: Scalability Analysis of Linearized Llama-3 Architectures across Model Sizes (1B to 8B). Liger demonstrates consistent scaling laws, outperforming LoLCATs by +6.8–11.5% absolute on average metrics while preserving 83–98% of base model capabilities with only 0.02B adaptation tokens.
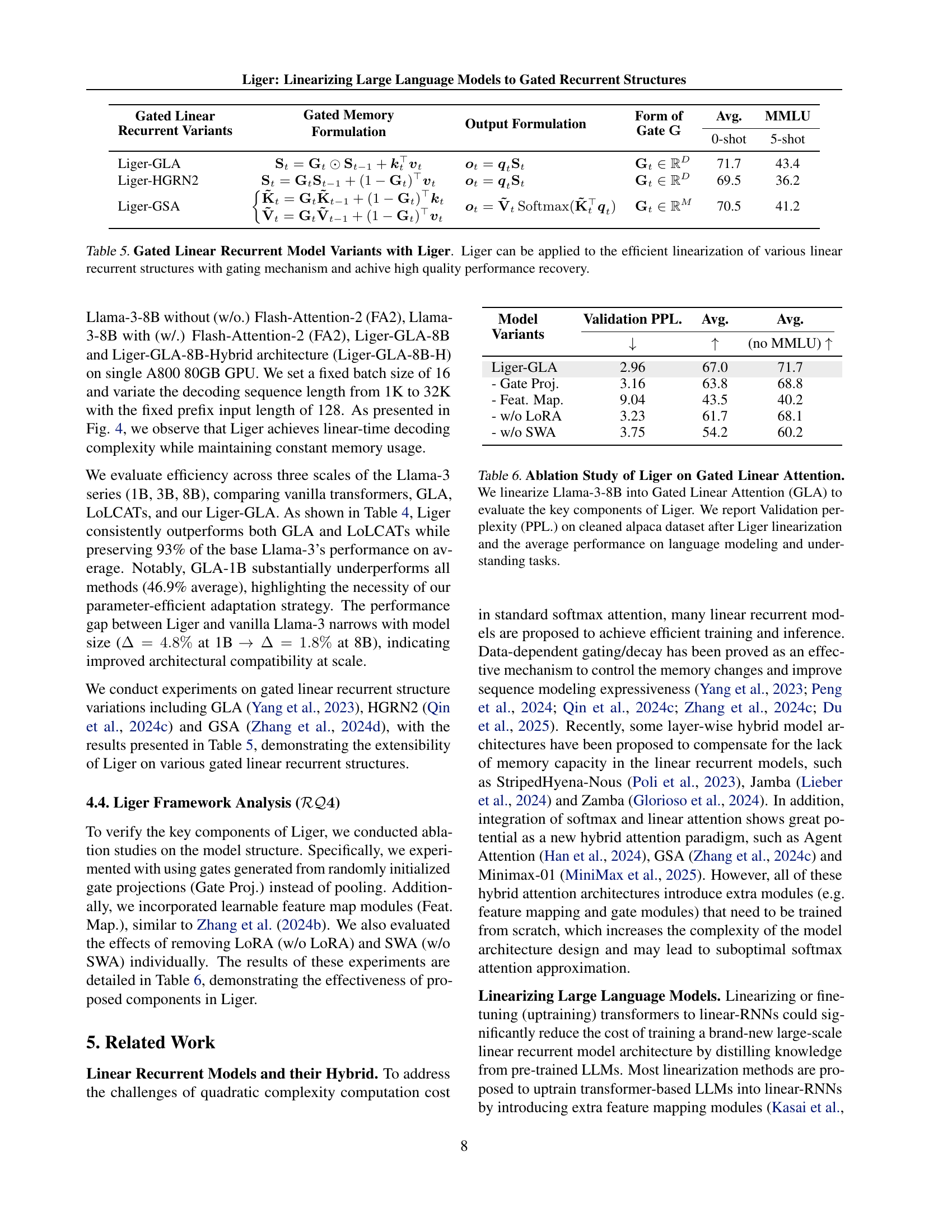
| Gated Linear Recurrent Variants | Gated Memory Formulation | Output Formulation | Form of Gate | Avg. | MMLU |
| 0-shot | 5-shot | ||||
| Liger-GLA | 71.7 | 43.4 | |||
| Liger-HGRN2 | 69.5 | 36.2 | |||
| Liger-GSA | 70.5 | 41.2 |
🔼 Table 5 presents several variations of gated linear recurrent models, showcasing the adaptability of the Liger method. The table compares different gating mechanisms (GLA, HGRN2, GSA) integrated within Liger, illustrating how the choice of gating mechanism impacts the final performance. Each row demonstrates the gated memory formulation, the output calculation, the type of gating parameter used (and its dimensions), and the resulting average performance on the MMLU benchmark, both with 0-shot and 5-shot evaluation settings. The results highlight Liger’s ability to effectively linearize various gated recurrent structures while achieving high-quality performance recovery.
read the caption
Table 5: Gated Linear Recurrent Model Variants with Liger. Liger can be applied to the efficient linearization of various linear recurrent structures with gating mechanism and achive high quality performance recovery.
| Model Variants | Validation PPL. | Avg. | Avg. |
| (no MMLU) | |||
| Liger-GLA | 2.96 | 67.0 | 71.7 |
| - Gate Proj. | 3.16 | 63.8 | 68.8 |
| - Feat. Map. | 9.04 | 43.5 | 40.2 |
| - w/o LoRA | 3.23 | 61.7 | 68.1 |
| - w/o SWA | 3.75 | 54.2 | 60.2 |
🔼 This table presents the results of an ablation study conducted to analyze the impact of different components within the Liger framework. The experiment involved linearizing the Llama-3-8B model into a Gated Linear Attention (GLA) architecture. Several variations of Liger were tested, each modifying a key component such as using randomly initialized gate projections instead of pooling, adding learnable feature maps, removing LoRA, or removing the Sliding Window Attention (SWA). The table reports the validation perplexity (PPL) on a cleaned Alpaca dataset after linearization, and average performance across various language modeling and understanding benchmarks. This allows for a quantitative assessment of the contribution of each component to the overall performance of Liger.
read the caption
Table 6: Ablation Study of Liger on Gated Linear Attention. We linearize Llama-3-8B into Gated Linear Attention (GLA) to evaluate the key components of Liger. We report Validation perplexity (PPL.) on cleaned alpaca dataset after Liger linearization and the average performance on language modeling and understanding tasks.
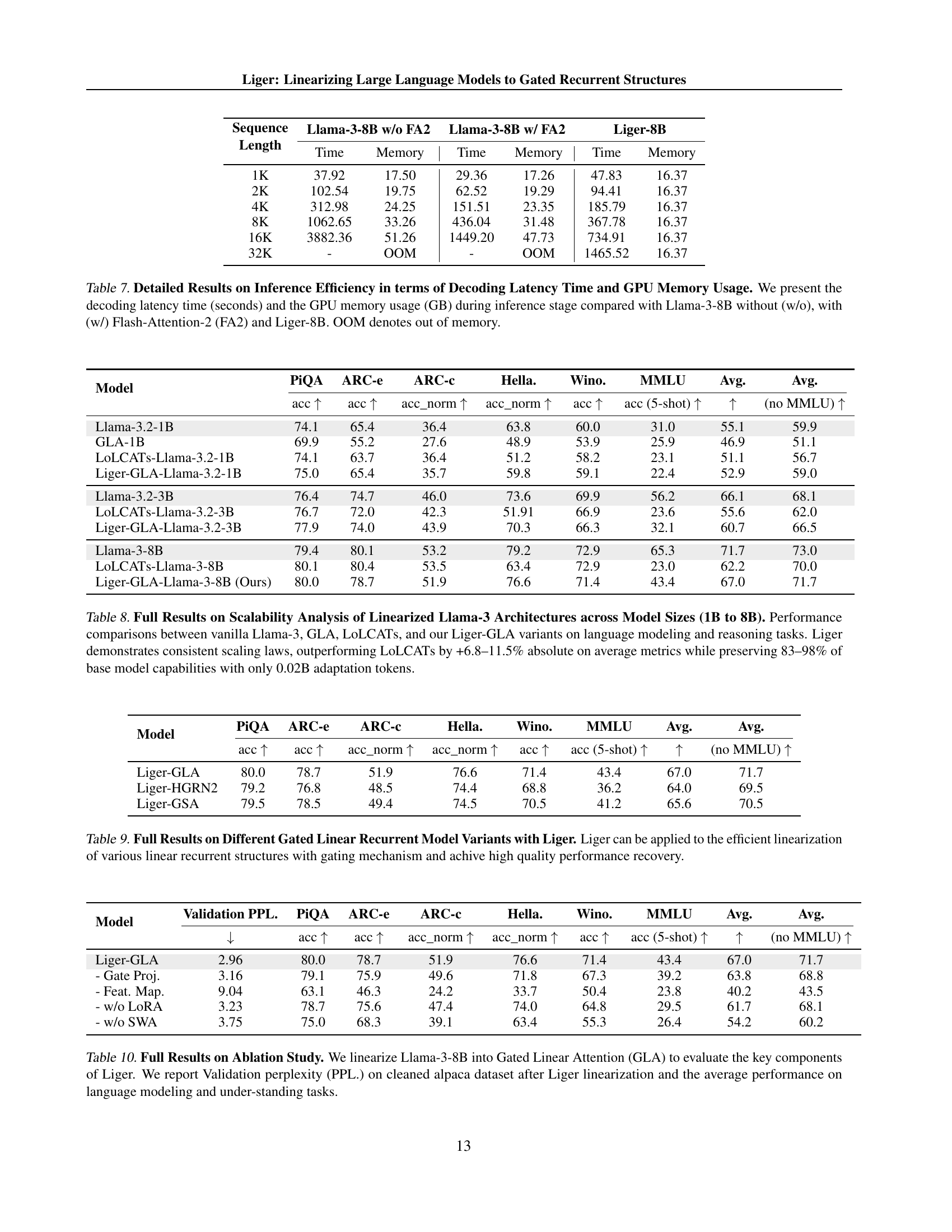
| Sequence Length | Llama-3-8B w/o FA2 | Llama-3-8B w/ FA2 | Liger-8B | |||
| Time | Memory | Time | Memory | Time | Memory | |
| 1K | 37.92 | 17.50 | 29.36 | 17.26 | 47.83 | 16.37 |
| 2K | 102.54 | 19.75 | 62.52 | 19.29 | 94.41 | 16.37 |
| 4K | 312.98 | 24.25 | 151.51 | 23.35 | 185.79 | 16.37 |
| 8K | 1062.65 | 33.26 | 436.04 | 31.48 | 367.78 | 16.37 |
| 16K | 3882.36 | 51.26 | 1449.20 | 47.73 | 734.91 | 16.37 |
| 32K | - | OOM | - | OOM | 1465.52 | 16.37 |
🔼 This table presents a detailed comparison of inference efficiency between different models, focusing on decoding latency and GPU memory usage. Three models are compared: Llama-3-8B without Flash-Attention-2 (FA2), Llama-3-8B with FA2, and Liger-8B. The comparison is made across various sequence lengths, from 1K to 32K tokens. The results show the decoding time (in seconds) and GPU memory usage (in GB) for each model and sequence length. The table highlights the significant memory advantage of Liger-8B, especially for long sequences, where Llama-3-8B with FA2 runs out of memory (OOM). This demonstrates Liger’s superior efficiency in terms of both time and memory consumption during inference.
read the caption
Table 7: Detailed Results on Inference Efficiency in terms of Decoding Latency Time and GPU Memory Usage. We present the decoding latency time (seconds) and the GPU memory usage (GB) during inference stage compared with Llama-3-8B without (w/o), with (w/) Flash-Attention-2 (FA2) and Liger-8B. OOM denotes out of memory.
| Model | PiQA | ARC-e | ARC-c | Hella. | Wino. | MMLU | Avg. | Avg. |
| acc | acc | acc_norm | acc_norm | acc | acc (5-shot) | (no MMLU) | ||
| Llama-3.2-1B | 74.1 | 65.4 | 36.4 | 63.8 | 60.0 | 31.0 | 55.1 | 59.9 |
| GLA-1B | 69.9 | 55.2 | 27.6 | 48.9 | 53.9 | 25.9 | 46.9 | 51.1 |
| LoLCATs-Llama-3.2-1B | 74.1 | 63.7 | 36.4 | 51.2 | 58.2 | 23.1 | 51.1 | 56.7 |
| Liger-GLA-Llama-3.2-1B | 75.0 | 65.4 | 35.7 | 59.8 | 59.1 | 22.4 | 52.9 | 59.0 |
| Llama-3.2-3B | 76.4 | 74.7 | 46.0 | 73.6 | 69.9 | 56.2 | 66.1 | 68.1 |
| LoLCATs-Llama-3.2-3B | 76.7 | 72.0 | 42.3 | 51.91 | 66.9 | 23.6 | 55.6 | 62.0 |
| Liger-GLA-Llama-3.2-3B | 77.9 | 74.0 | 43.9 | 70.3 | 66.3 | 32.1 | 60.7 | 66.5 |
| Llama-3-8B | 79.4 | 80.1 | 53.2 | 79.2 | 72.9 | 65.3 | 71.7 | 73.0 |
| LoLCATs-Llama-3-8B | 80.1 | 80.4 | 53.5 | 63.4 | 72.9 | 23.0 | 62.2 | 70.0 |
| Liger-GLA-Llama-3-8B (Ours) | 80.0 | 78.7 | 51.9 | 76.6 | 71.4 | 43.4 | 67.0 | 71.7 |
🔼 Table 8 presents a comprehensive scalability analysis of the Liger model for linearizing Llama-3 architectures of varying sizes (1B, 3B, and 8B parameters). It compares the performance of Liger-GLA (Liger with Gated Linear Attention) against baseline models: vanilla Llama-3, GLA (Gated Linear Attention), and LoLCATs (Linearizing Large Language Models with Low-Rank Adaptation). The comparison is made across several language modeling and reasoning benchmarks. Key metrics include accuracy scores on tasks such as PIQA, ARC-e, ARC-c, HellaSwag, Winogrande, and MMLU. The table highlights Liger’s consistent scaling behavior, demonstrating superior performance compared to LoLCATs (a +6.8% to +11.5% improvement in average accuracy) while maintaining a high level of performance (83–98%) relative to the original Llama-3 models. This is achieved using only 0.02 billion adaptation tokens during the fine-tuning process. The results showcase the efficiency and scalability of the Liger approach for linearizing large language models.
read the caption
Table 8: Full Results on Scalability Analysis of Linearized Llama-3 Architectures across Model Sizes (1B to 8B). Performance comparisons between vanilla Llama-3, GLA, LoLCATs, and our Liger-GLA variants on language modeling and reasoning tasks. Liger demonstrates consistent scaling laws, outperforming LoLCATs by +6.8–11.5% absolute on average metrics while preserving 83–98% of base model capabilities with only 0.02B adaptation tokens.
| Model | PiQA | ARC-e | ARC-c | Hella. | Wino. | MMLU | Avg. | Avg. |
| acc | acc | acc_norm | acc_norm | acc | acc (5-shot) | (no MMLU) | ||
| Liger-GLA | 80.0 | 78.7 | 51.9 | 76.6 | 71.4 | 43.4 | 67.0 | 71.7 |
| Liger-HGRN2 | 79.2 | 76.8 | 48.5 | 74.4 | 68.8 | 36.2 | 64.0 | 69.5 |
| Liger-GSA | 79.5 | 78.5 | 49.4 | 74.5 | 70.5 | 41.2 | 65.6 | 70.5 |
🔼 Table 9 presents a comprehensive evaluation of Liger’s adaptability to various gated linear recurrent neural network (RNN) architectures. It showcases the performance of Liger when applied to three different gated RNN variants: Liger-GLA, Liger-HGRN2, and Liger-GSA, each incorporating a distinct gating mechanism. The results demonstrate Liger’s ability to efficiently linearize these diverse architectures, achieving high-quality performance recovery. The table highlights the average accuracy across multiple language modeling and understanding benchmarks for each variant, emphasizing Liger’s versatility and effectiveness in achieving efficient and high-performing linearization across diverse RNN structures.
read the caption
Table 9: Full Results on Different Gated Linear Recurrent Model Variants with Liger. Liger can be applied to the efficient linearization of various linear recurrent structures with gating mechanism and achive high quality performance recovery.
| Model | Validation PPL. | PiQA | ARC-e | ARC-c | Hella. | Wino. | MMLU | Avg. | Avg. |
| acc | acc | acc_norm | acc_norm | acc | acc (5-shot) | (no MMLU) | |||
| Liger-GLA | 2.96 | 80.0 | 78.7 | 51.9 | 76.6 | 71.4 | 43.4 | 67.0 | 71.7 |
| - Gate Proj. | 3.16 | 79.1 | 75.9 | 49.6 | 71.8 | 67.3 | 39.2 | 63.8 | 68.8 |
| - Feat. Map. | 9.04 | 63.1 | 46.3 | 24.2 | 33.7 | 50.4 | 23.8 | 40.2 | 43.5 |
| - w/o LoRA | 3.23 | 78.7 | 75.6 | 47.4 | 74.0 | 64.8 | 29.5 | 61.7 | 68.1 |
| - w/o SWA | 3.75 | 75.0 | 68.3 | 39.1 | 63.4 | 55.3 | 26.4 | 54.2 | 60.2 |
🔼 This table presents a detailed ablation study on the Liger model’s key components. Llama-3-8B is linearized into Gated Linear Attention (GLA), and various modifications are tested, including removing key components like the sliding window attention (SWA) or using randomly initialized gate projections instead of pooling. The results show the impact of each component on both the validation perplexity (PPL) and the average performance across language modeling and understanding tasks. This allows for a comprehensive evaluation of the contribution of each individual component in Liger.
read the caption
Table 10: Full Results on Ablation Study. We linearize Llama-3-8B into Gated Linear Attention (GLA) to evaluate the key components of Liger. We report Validation perplexity (PPL.) on cleaned alpaca dataset after Liger linearization and the average performance on language modeling and under-standing tasks.
Full paper#