TL;DR#
Large Language Models(LLMs) must be uncertainty aware, but current methods focus on specific uncertainties while ignoring others. This study explores token-wise entropy and model-as-judge to assess multiple-choice questions across different topics. The experiments use Phi-4, Mistral and Qwen with sizes from 1.5B to 72B and 14 topics to estimate uncertainty.
The paper finds that response entropy predicts errors in knowledge-dependent domains and indicates question difficulty. The correlation vanishes for reasoning-dependent domains. Data-related entropy is important for uncertainty estimates while model-as-judge needs refining. Existing MMLU-Pro samples are biased and should balance reasoning for fair LLM assessment. Thus this paper facilitates a reliable deployment of LLMs.
Key Takeaways#
Why does it matter?#
This paper advances LLM evaluation by pinpointing the conditions where uncertainty estimates are reliable. It also emphasizes the need for enhanced datasets that consider reasoning complexity and topic balance, guiding the creation of more robust and trustworthy LLMs.
Visual Insights#

🔼 This figure illustrates the pipeline used to evaluate the uncertainty estimation of large language models (LLMs) in a multiple-choice question answering setting. It starts with a set of multiple-choice questions from the MMLU-Pro dataset, which are then processed by various LLMs. The pipeline then uses several techniques to estimate uncertainty, including token-wise entropy and model-as-judge (MASJ), and employs a separate model to assess various aspects of question complexity (reasoning requirements, knowledge requirements, and number of steps). The results, including correctness labels, are finally used to calculate ROC-AUC scores which are used to evaluate the effectiveness of the uncertainty estimation methods.
read the caption
Figure 1. Question complexity evaluation pipeline. See more details in the methods section
| Category | Sample Count |
|---|---|
| Mathematics | 1351 |
| Physics | 1299 |
| Chemistry | 1132 |
| Law | 1101 |
| Engineering | 969 |
| Economics | 844 |
| Health | 818 |
| Psychology | 798 |
| Business | 789 |
| Biology | 717 |
| Philosophy | 499 |
| Computer Science | 410 |
| History | 381 |
| Other | 924 |
🔼 This table shows the distribution of questions across different categories in the MMLU-Pro dataset. It lists 14 scientific categories (Mathematics, Physics, Chemistry, Law, Engineering, Economics, Health, Psychology, Business, Biology, Philosophy, Computer Science, History, and Other) and the number of questions in the MMLU-Pro dataset belonging to each category. This provides context on the size and diversity of the dataset used for evaluating the performance of large language models (LLMs).
read the caption
Table 1. MMLU-Pro Category Distribution
In-depth insights#
LLM Uncertainty#
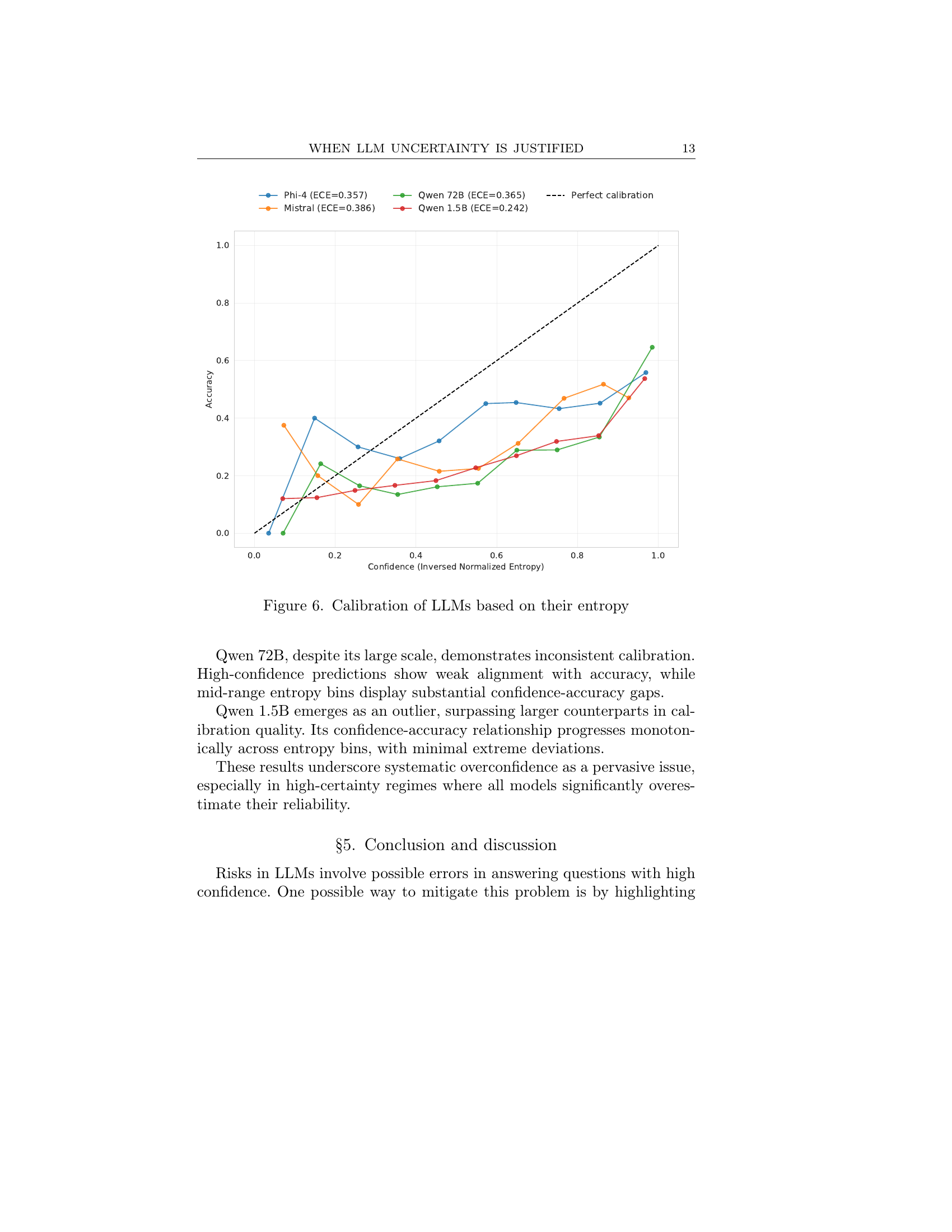
LLM uncertainty is a critical area, especially with their increasing use in high-stakes applications. It arises from multiple sources: the model itself (epistemic uncertainty due to lack of knowledge) and the data (aleatoric uncertainty stemming from noise or complexity). Addressing this requires more than just improving overall accuracy; it demands a deeper understanding of when and why a model is uncertain. Methods like entropy-based measures and model-as-judge approaches offer insights, but their effectiveness varies across different tasks and domains. For instance, a model might be confident but wrong due to format overfitting, highlighting the need for better calibration. Also, certain issues like hallucinations need to be addressed to ensure the model works smoothly.
Entropy vs. MASJ#
Entropy and MASJ (Model-as-Judge) represent distinct approaches to gauging LLM uncertainty. Entropy measures the randomness of token predictions, reflecting the model’s confidence in its output, where lower entropy suggests greater certainty. Conversely, MASJ utilizes another LLM to evaluate the generated response quality. The paper contrasts their effectiveness across diverse question domains. Entropy may excel in knowledge-dependent areas by indicating information retrieval certainty, while MASJ’s performance might vary based on the evaluator model’s capabilities. The paper likely investigates scenarios where one method surpasses the other, examining their correlation with question complexity and reasoning demands to pinpoint the most suitable technique for specific uncertainty assessment tasks. The trade-offs between computation cost & reliability could be discussed. Ultimately, the research aims to provide a nuanced understanding of these methods and their application, aiming to improve the reliability of LLMs, especially in critical domains.
MMLU-Pro Biases#
While the paper doesn’t explicitly have a section titled “MMLU-Pro Biases,” the research uncovers crucial biases within the dataset. The finding that existing MMLU-Pro samples are biased points towards a potential imbalance in the complexity of questions. The paper suggests balancing the amount of reasoning required for different subdomains. There is a similar kind of problem for the topic itself. The presence of biases directly affects the fairness of LLM performance assessment. Furthermore, the discovery of varying reasoning demands depending on the topic underscores the need for a more nuanced evaluation approach that accounts for these inherent differences. By directly addressing these dataset flaws, the research advocates for a more rigorous and equitable evaluation landscape in the field of large language models.
Reasoning Steps#
Reasoning steps are a key element in understanding how LLMs approach complex tasks. This refers to the number of sequential logical operations a model undertakes to arrive at an answer. A higher number of steps often indicates a more challenging problem, demanding intricate analysis. Determining the nature and quantity of reasoning involved unveils the LLM’s cognitive pathways, showing knowledge application and intricate problem-solving skills. A detailed examination of reasoning sequences gives insights on LLM strength and shortcomings, informing strategies for performance enhancement. Accurately mapping reasoning depth helps tailor models to tasks, improve outputs and enhance their performance in diverse problem-solving domains.
Model Size Matters#
Model size significantly impacts LLM performance, especially in complex tasks. Larger models, with more parameters, tend to capture intricate patterns and relationships in data, leading to better accuracy and generalization. Increased capacity allows for a more nuanced understanding of context, enabling more coherent and relevant responses. However, the benefits of larger models come at a cost: they require substantial computational resources for training and inference, potentially limiting accessibility. Furthermore, simply increasing model size does not guarantee improved performance; architectural innovations, training data quality, and optimization techniques also play crucial roles. The optimal model size is therefore a trade-off between desired accuracy, available resources, and the specific demands of the task at hand. Additionally, entropy separation tends to correlate with model scale, meaning the divergence between correct and incorrect results is clearer in larger models.
More visual insights#
More on figures
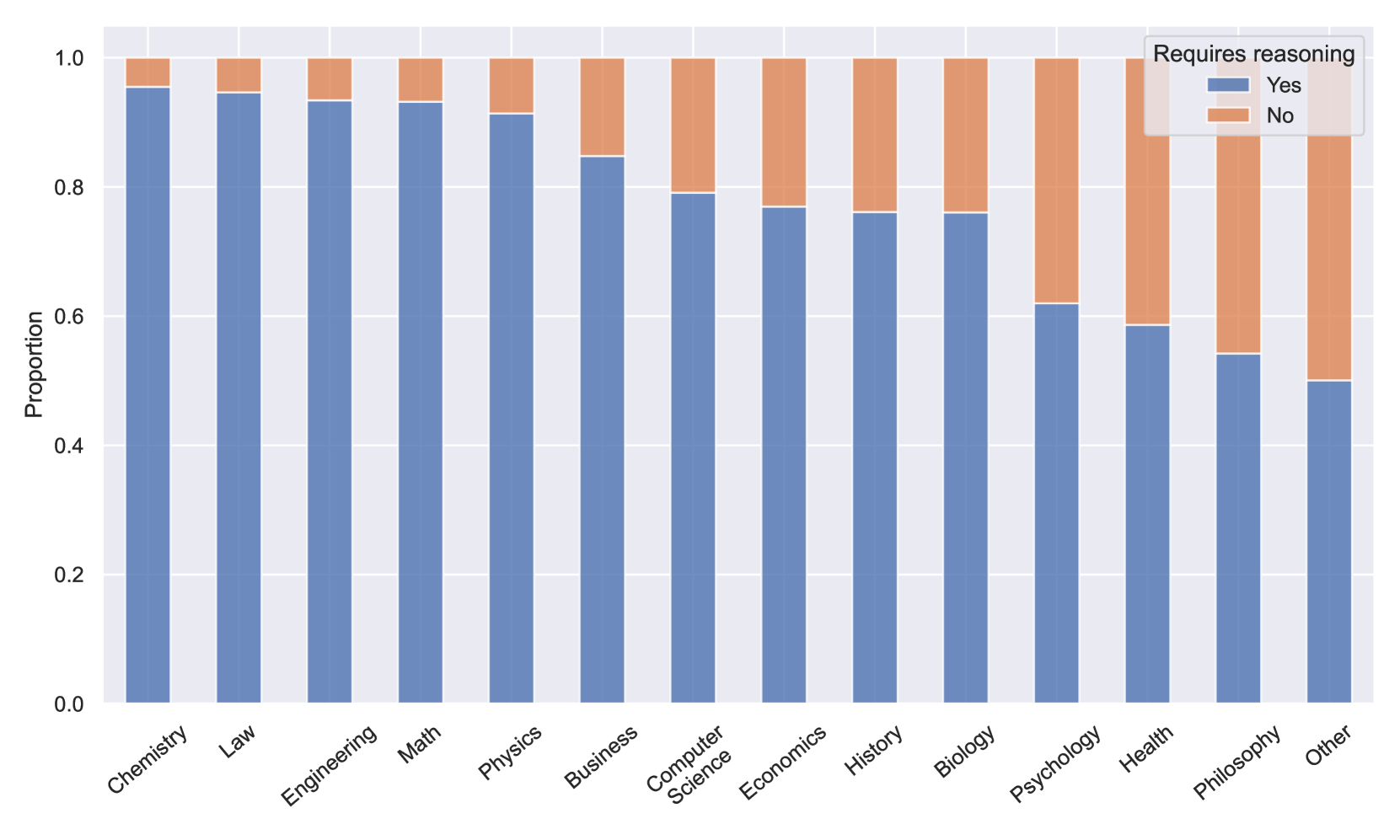
🔼 This figure shows the distribution of questions across different topics that require complex reasoning, as determined by a model-as-judge (MASJ) approach. The x-axis represents the different subject areas (e.g., Computer Science, Economics, Biology, etc.), while the y-axis represents the percentage of questions within each subject that required complex reasoning according to the MASJ. This visualization helps illustrate the variation in reasoning demands across different domains within the MMLU-Pro dataset.
read the caption
((a)) Distribution of questions that require complex reasoning

🔼 This bar chart visualizes the distribution of questions across different levels of required reasoning steps, as determined by a model-as-judge (MASJ) approach. Each bar represents a category (e.g., Biology, Economics, etc.) from the MMLU-Pro dataset, and its height corresponds to the number of questions in that category. The bars are further segmented into sub-sections representing three levels of reasoning complexity: low, medium, and high. This visualization reveals how the distribution of reasoning requirements varies across different subject areas within the dataset.
read the caption
((b)) Distribution of the required number of reasoning steps

🔼 This figure shows the results of using a Model-as-Judge (MASJ) approach to estimate the reasoning requirement and the number of reasoning steps needed for different questions in the MMLU-Pro dataset. The left subplot displays the distribution of questions categorized as requiring complex reasoning versus those that do not. The right subplot illustrates the distribution of the estimated number of reasoning steps required for each question. The distribution varies considerably across different subject areas, with some topics like engineering requiring substantially more reasoning than others like philosophy.
read the caption
Figure 2. Estimation by MASJ of the required reasoning amount. Better to view in zoom

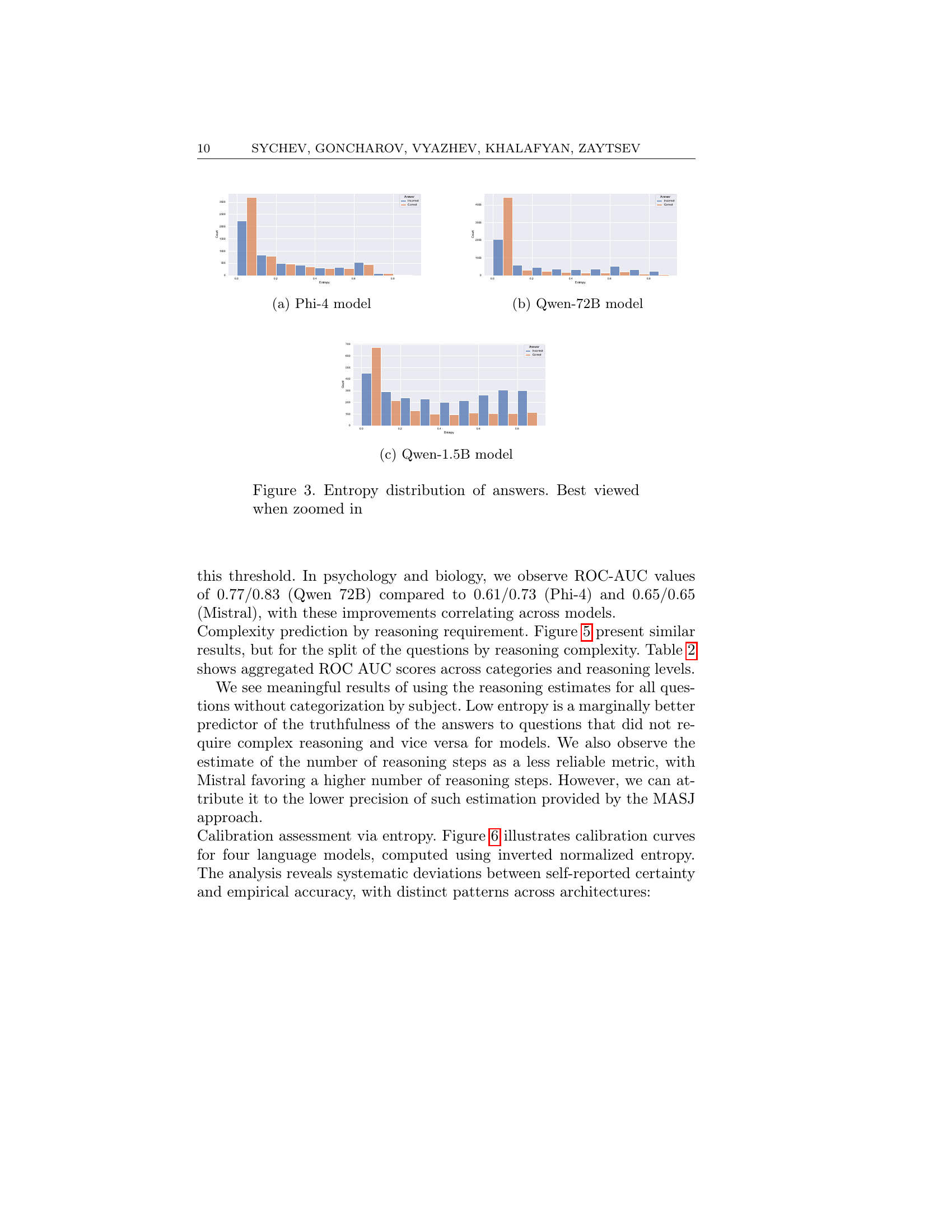
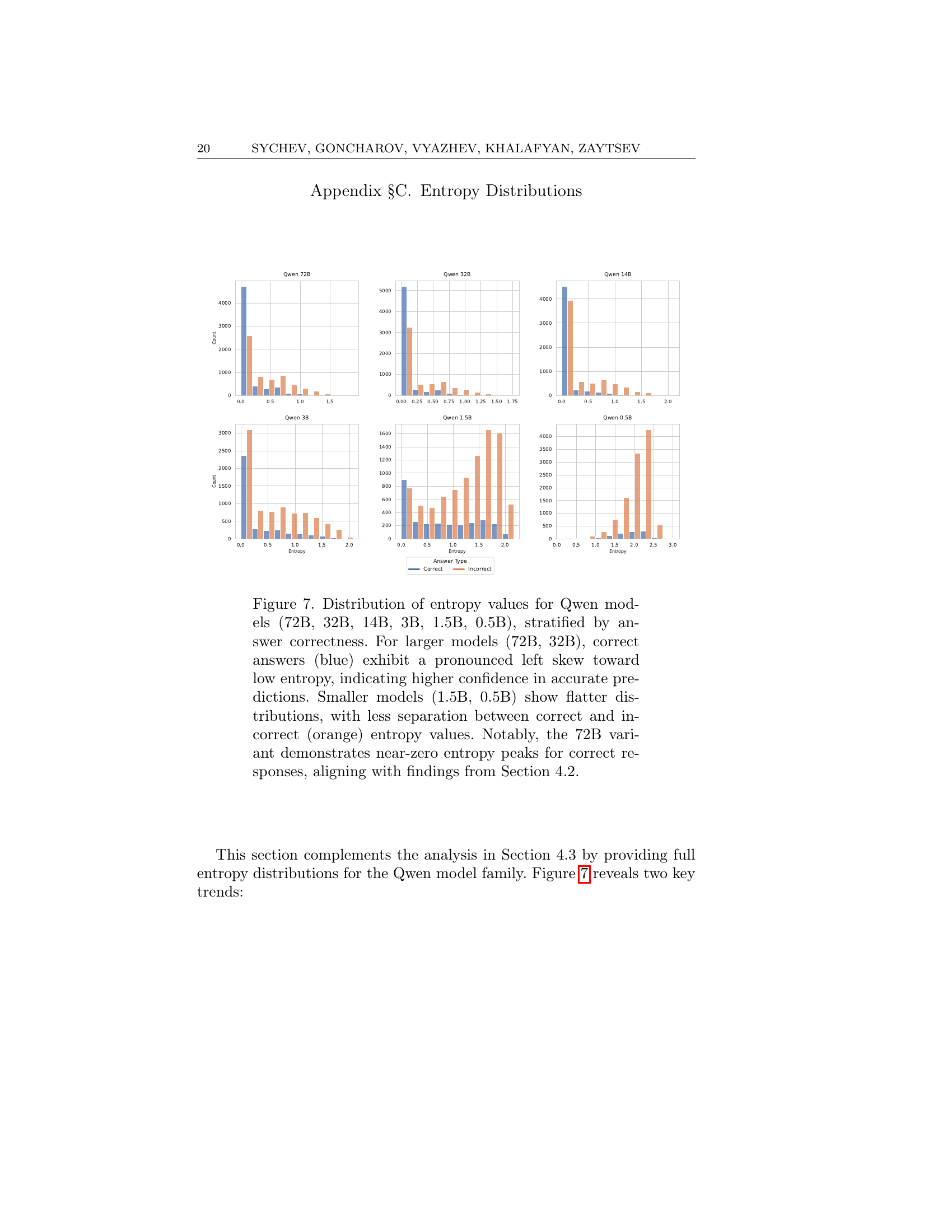
🔼 This figure shows the distribution of entropy values for the Phi-4 language model. The x-axis represents the entropy values, while the y-axis represents the frequency or count of answers with those entropy values. The figure is separated into two bars for each entropy value, representing the number of correct and incorrect answers at that entropy level. This visualization helps to understand the relationship between entropy (a measure of uncertainty) and the accuracy of the model’s predictions.
read the caption
((a)) Phi-4 model

🔼 This figure shows the distribution of entropy values for the Qwen-72B language model’s answers, categorized by whether the answer is correct or incorrect. The x-axis represents the entropy values, and the y-axis represents the count of answers. The distribution for correct answers is skewed towards lower entropy values, while incorrect answers have a flatter and more spread out distribution across entropy levels, indicating higher uncertainty in incorrect responses. This visualization supports the paper’s findings regarding the correlation between entropy and model prediction accuracy.
read the caption
((b)) Qwen-72B model

🔼 This figure shows the distribution of entropy values for the Qwen-1.5B language model. The x-axis represents the entropy values, and the y-axis represents the count of answers with that specific entropy. The bars are separated into correct and incorrect answers, allowing for a visual comparison of entropy levels in relation to answer accuracy. This visualization helps to understand how well the entropy metric captures model uncertainty for this specific model.
read the caption
((c)) Qwen-1.5B model

🔼 This figure displays the distribution of entropy values for answers generated by different language models. It shows separate distributions for correct and incorrect answers, allowing for a visual comparison of entropy levels across various response types. The distributions reveal insights into the relationship between model confidence (as reflected in entropy) and the accuracy of the generated answers. It helps in understanding how well the entropy measure correlates with the models’ ability to accurately assess its uncertainty.
read the caption
Figure 3. Entropy distribution of answers. Best viewed when zoomed in
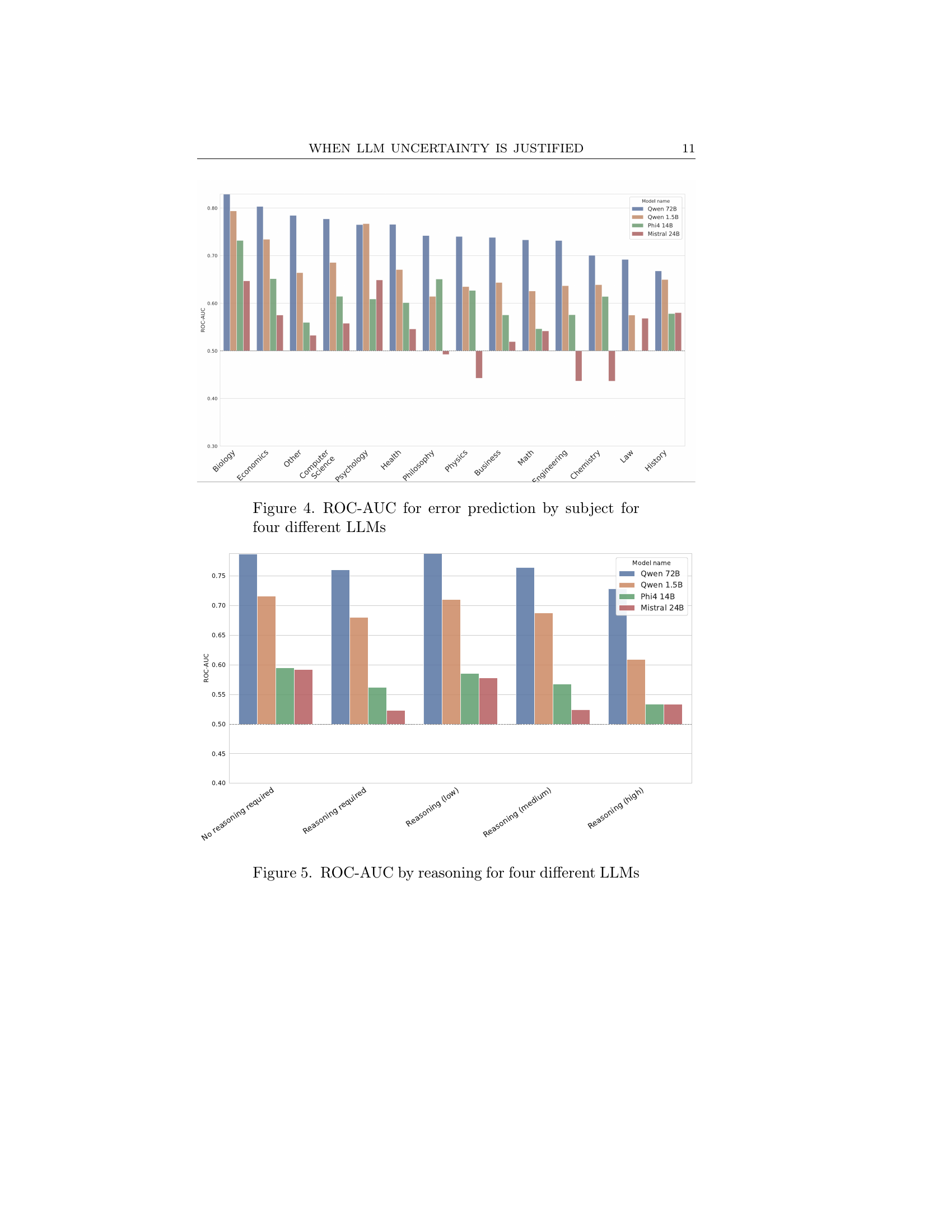
🔼 This figure displays the area under the ROC curve (ROC-AUC) for four different large language models (LLMs): Phi-4, Mistral, Qwen 1.5B, and Qwen 72B. The ROC-AUC values are presented for each LLM’s ability to predict errors in answering questions categorized by subject. Higher ROC-AUC values indicate better performance in error prediction. The subjects appear to represent diverse academic fields, and the bars show the ROC-AUC score for each model within each subject.
read the caption
Figure 4. ROC-AUC for error prediction by subject for four different LLMs

🔼 This figure shows the area under the ROC curve (ROC-AUC) for four different large language models (LLMs): Qwen 72B, Qwen 1.5B, Phi-4 14B, and Mistral 24B. The ROC-AUC values are displayed for different levels of reasoning required to answer the questions in the MMLU-Pro dataset. The x-axis categorizes the questions based on their reasoning requirements: ’no reasoning required’, ‘reasoning required’, ‘reasoning (low)’, ‘reasoning (medium)’, and ‘reasoning (high)’. The y-axis represents the ROC-AUC score, indicating the model’s performance in predicting whether an answer is correct or incorrect based on its associated entropy value. Higher ROC-AUC values suggest better performance.
read the caption
Figure 5. ROC-AUC by reasoning for four different LLMs
More on tables
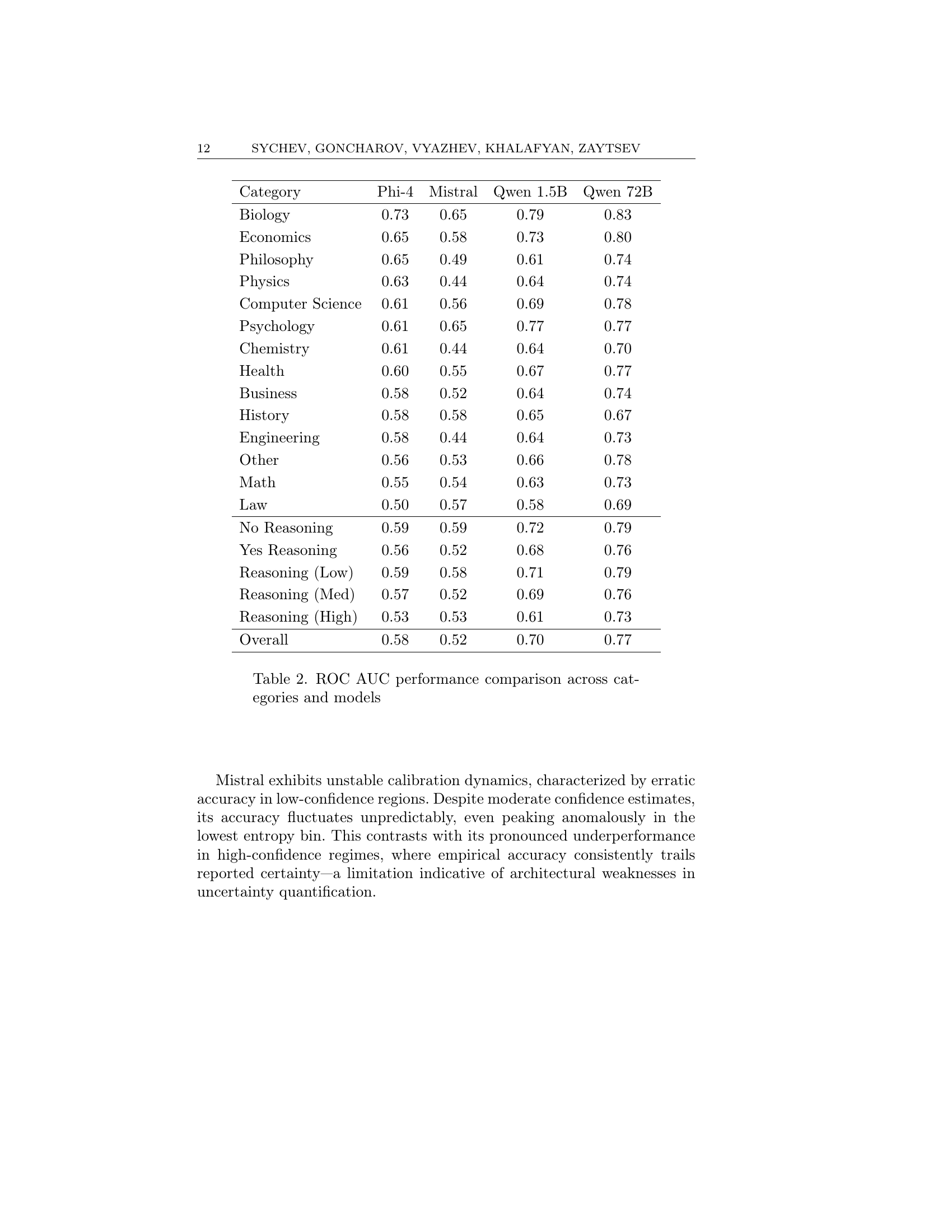
| Category | Phi-4 | Mistral | Qwen 1.5B | Qwen 72B |
|---|---|---|---|---|
| Biology | 0.73 | 0.65 | 0.79 | 0.83 |
| Economics | 0.65 | 0.58 | 0.73 | 0.80 |
| Philosophy | 0.65 | 0.49 | 0.61 | 0.74 |
| Physics | 0.63 | 0.44 | 0.64 | 0.74 |
| Computer Science | 0.61 | 0.56 | 0.69 | 0.78 |
| Psychology | 0.61 | 0.65 | 0.77 | 0.77 |
| Chemistry | 0.61 | 0.44 | 0.64 | 0.70 |
| Health | 0.60 | 0.55 | 0.67 | 0.77 |
| Business | 0.58 | 0.52 | 0.64 | 0.74 |
| History | 0.58 | 0.58 | 0.65 | 0.67 |
| Engineering | 0.58 | 0.44 | 0.64 | 0.73 |
| Other | 0.56 | 0.53 | 0.66 | 0.78 |
| Math | 0.55 | 0.54 | 0.63 | 0.73 |
| Law | 0.50 | 0.57 | 0.58 | 0.69 |
| No Reasoning | 0.59 | 0.59 | 0.72 | 0.79 |
| Yes Reasoning | 0.56 | 0.52 | 0.68 | 0.76 |
| Reasoning (Low) | 0.59 | 0.58 | 0.71 | 0.79 |
| Reasoning (Med) | 0.57 | 0.52 | 0.69 | 0.76 |
| Reasoning (High) | 0.53 | 0.53 | 0.61 | 0.73 |
| Overall | 0.58 | 0.52 | 0.70 | 0.77 |
🔼 This table presents the Area Under the ROC Curve (AUC) values, a measure of a model’s performance in distinguishing between correct and incorrect answers, for four different Large Language Models (LLMs): Phi-4, Mistral, Qwen-1.5B, and Qwen-72B. The AUC values are broken down by category (e.g., Biology, Economics, Psychology) and by reasoning requirement (No Reasoning, Yes Reasoning, and three levels of reasoning difficulty: Low, Medium, High). A higher AUC value indicates better performance.
read the caption
Table 2. ROC AUC performance comparison across categories and models
| You are an expert in the topic of the question. Please act as an impartial judge and evaluate the complexity of the multiple-choice question with options below. Begin your evaluation by providing a short explanation. Be as objective as possible. After providing your explanation, you must not answer the question. You must rate the question complexity as a number from 0 to 1 following the following scale as a reference: |
| high_school_and_ easier - 0.0-0.22, |
| undergraduate_easy - 0.2-0.4, |
| undergraduate_hard - 0.4-0.6, |
| graduate - 0.6-0.8, |
| postgraduate - 0.8-1.0. |
| You must return the complexity by strictly following this format: " [[complexity]]", |
| for example: "Your explanation… Complexity: [[0.55]]", which corresponds to a hard question at the undergraduate level. |
🔼 This table presents the prompt used for the numerical model-as-judge in the study. The prompt instructs the model to act as an impartial judge and evaluate the complexity of a multiple-choice question. The model should provide a short explanation of its evaluation, but should not answer the question itself. The model is given a scale for rating the question’s complexity ranging from 0.0 to 1.0, corresponding to different educational levels, from high school to postgraduate studies. The prompt specifies the format for returning the complexity score, which must follow the pattern: ‘[[complexity]]:’ where the value should be a number between 0.0 and 1.0.
read the caption
Table 3. Prompt for Numerical model-as-judge
| You are an expert in the topic of the question. Please act as an impartial judge and evaluate the complexity of the multiple-choice question with options below. Begin your evaluation by providing a short explanation. Be as objective as possible. After providing your explanation, you must not answer the question. You must rate the question complexity by strictly following the scale: |
| high_school_and_easier, |
| undergraduate_easy, |
| undergraduate_hard, |
| graduate, |
| postgraduate. |
| You must return the complexity by strictly following this format: "[[complexity]]", |
| for example: "Your explanation… Complexity: [[undergraduate]]", which corresponds to the undergraduate level. |
🔼 This table presents the prompt used for the nominal Model-as-Judge (MASJ) approach in the paper. The MASJ approach uses a large language model to evaluate the complexity of a multiple-choice question. This specific prompt instructs the model to act as an impartial judge, providing a short explanation of its evaluation before assigning a complexity label. The labels are categorical and range from high school and easier to postgraduate, allowing for a qualitative assessment of the question’s difficulty.
read the caption
Table 4. Prompt for Nominal model-as-judge
| You are an expert in the topic of the question. Please act as an impartial judge and evaluate the complexity of the multiple-choice question with options below. |
| Begin your evaluation by providing a short explanation. Be as objective as possible. After providing your explanation, you must not answer the question. |
| You must rate the question complexity by strictly following the criteria: |
| 1) [[Requires knowledge]] - do we need highly specific knowledge from the domain to answer this question? Valid answers: yes, no; |
| 2) [[Requires reasoning]] - do we need complex reasoning with multiple logical steps to answer this question? Valid answers: yes, no; |
| 3) [[Number of reasoning steps]] - how many reasoning steps do you need to answer this question? Valid answers: low, medium, high. |
| Your answer must strictly follow this format: "[[Requires knowledge: answer]] [[Requires reasoning: answer]] [[Number of reasoning steps: answer]]". |
| Example 1: "Your explanation… [[Requires knowledge: yes]] [[Requires reasoning: no]] [[Number of reasoning steps: low]]". |
| Example 2: "Your explanation… [[Requires knowledge: no]] [[Requires reasoning: yes]] [[Number of reasoning steps: high]]". |
| Example 3: "Your explanation… [[Requires knowledge: yes]] [[Requires reasoning: yes]] [[Number of reasoning steps: medium]]". |
| Example 4: "Your explanation… [[Requires knowledge: no]] [[Requires reasoning: no]] [[Number of reasoning steps: low]]". |
🔼 This table presents the prompt used to elicit reasoning level information from a model-as-judge. The prompt instructs the model to act as an expert, evaluating the complexity of a multiple-choice question. It requests an explanation of the assessment and then prompts the model to classify the question based on its reasoning requirements (yes/no), and the number of reasoning steps involved (low, medium, high). The format of the output response is specified to ensure consistent data collection.
read the caption
Table 5. Prompt for Reasoning level estimate
| Which of the following criticisms of Llewellyn’s distinction between the grand and formal styles of legal reasoning is the most compelling? |
| 1. There is no distinction between the two forms of legal reasoning. |
| 2. Judges are appointed to interpret the law, not to make it. |
| 3. It is misleading to pigeon-hole judges in this way. |
| 4. Judicial reasoning is always formal. |
🔼 This table presents an example of a multiple-choice question from the Law category within the MMLU-Pro dataset. The question assesses understanding of legal reasoning styles, specifically Llewellyn’s distinction between grand and formal styles. It demonstrates the type of complex reasoning and legal knowledge required to answer questions in this category of the dataset. The four options provided are intended to evaluate the test-taker’s grasp of the nuances of legal argumentation.
read the caption
Table 6. Example of a question from Law category
| A 66-year-old client who is depressed, has rhythmic hand movements, and has a flattened affect is probably suffering from: |
| 1. Huntington’s disease |
| 2. Creutzfeldt-Jakob disease |
| 3. Multiple Sclerosis |
| 4. Alzheimer’s disease |
| 5. Parkinson’s disease |
| 6. Vascular Dementia |
| 7. Frontotemporal Dementia |
| 8. Schizophrenia |
| 9. A right frontal lobe tumor |
| 10. Bipolar Disorder |
🔼 This table shows an example of a multiple choice question from the Psychology category of the MMLU-Pro dataset used in the study. The question presents a case study of a 66-year-old patient with specific symptoms and asks the reader to identify the most likely diagnosis from a list of ten neurological and psychiatric disorders. This illustrates the type of questions included in the Psychology section of the dataset and the level of detail and reasoning required.
read the caption
Table 7. Example of a question from Psychology category
| A cumulative compound motor has a varying load upon it which requires a variation in armature current from 50 amp to 100 amp. |
| If the series-field current causes the air-gap flux to change by 3 percent for each 10 amp of armature current, find the ratio of torques developed for the two values of armature current. |
| 1. 2.26 |
| 2. 0.66 |
| 3. 3.95 |
| 4. 1.00 |
| 5. 2.89 |
| 6. 1.75 |
| 7. 4.12 |
| 8. 1.15 |
| 9. 0.87 |
| 10. 3.40 |
🔼 This table presents a sample multiple-choice question from the Engineering category of the MMLU-Pro dataset. The question involves a cumulative compound motor with a varying load, requiring a change in armature current. The task is to calculate the ratio of torques developed for two given armature current values, testing the examinee’s understanding of electrical machine principles and their ability to solve related engineering problems.
read the caption
Table 8. Example of a question from Engineering category
Full paper#