Sketch-of-Thought: Efficient LLM Reasoning with Adaptive Cognitive-Inspired Sketching

2503.05179

Simon A. Aytes et el.

🤗 2025-03-10

TL;DR
#

Large language models excel at reasoning, but often use too many tokens, increasing computational cost. This paper introduces Sketch-of-Thought (SoT), a new prompting framework to make LLM reasoning more efficient. It combines cognitive-inspired methods with linguistic constraints to minimize token usage while maintaining accuracy.

SoT has three reasoning paradigms: Conceptual Chaining, Chunked Symbolism, and Expert Lexicons. A lightweight router model selects the best approach for each task. Evaluations across 15 datasets (including multilingual and multimodal) show SoT reduces token usage by up to 76% with minimal accuracy impact and sometimes even improves accuracy.

Key Takeaways
#

Why does it matter?
#

This paper is important because it tackles the growing verbosity of LLM reasoning directly. SoT’s cognitive-inspired approach offers a promising direction for creating more efficient AI systems, which is particularly crucial for resource-constrained applications. It also opens new research avenues such as how to combine SoT with other reasoning approaches.

Visual Insights
#

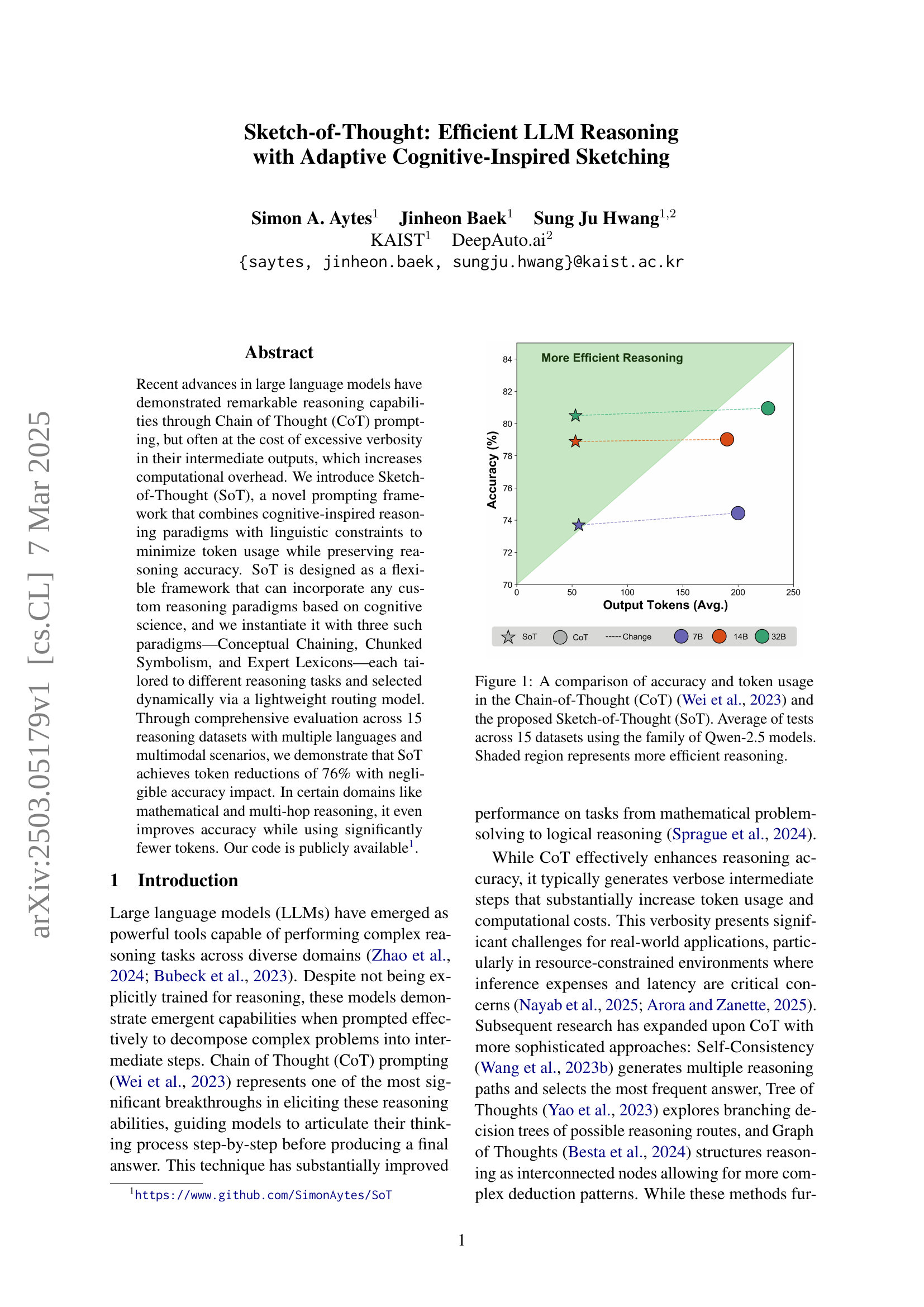
🔼 This figure compares the performance of two large language model (LLM) prompting techniques, Chain-of-Thought (CoT) and the proposed Sketch-of-Thought (SoT), in terms of accuracy and the number of tokens used. The results are averaged across 15 different reasoning datasets and utilize the Qwen-2.5 family of LLMs. The shaded region highlights the area where the model demonstrates more efficient reasoning (higher accuracy with fewer tokens). SoT is shown to be superior to CoT in this regard, offering comparable accuracy with a significantly reduced number of tokens.
read the caption
Figure 1: A comparison of accuracy and token usage in the Chain-of-Thought (CoT) Wei et al. (2023) and the proposed Sketch-of-Thought (SoT). Average of tests across 15 datasets using the family of Qwen-2.5 models. Shaded region represents more efficient reasoning.

Reasoning Task
	Mathematical		Commonsense		Logical		Multi-Hop		Scientific		Specialized		Overall
Method	%	Tokens	%	Tokens	%	Tokens	%	Tokens	%	Tokens	%	Tokens	% $\uparrow$	Tokens $\downarrow$	Red. $\uparrow$	$\Delta$ Acc $\uparrow$
Qwen-2.5-32B
CoT	84.17	221	90.33	186	71.23	297	79.44	154	92.89	212	67.66	291	80.95	227	-	-
SoT	86.94	88	90.66	30	71.00	65	81.89	43	91.33	31	61.11	62	80.49	53	76.22	-0.46
SC+CoT	84.33	665	91.00	560	71.67	892	81.00	464	93.34	638	67.33	875	81.44	682	-	-
SC+SoT	87.50	265	90.66	92	71.33	197	82.67	129	92.00	94	61.66	187	80.97	161	76.22	-0.47
Qwen-2.5-14B
CoT	83.00	189	90.44	155	67.00	248	77.67	148	90.89	164	65.11	234	79.02	190	-	-
SoT	82.72	78	89.78	35	67.44	63	79.89	45	90.89	37	62.56	62	78.88	53	71.80	-0.14
SC+CoT	83.17	569	92.33	467	69.33	744	76.33	446	91.00	493	66.33	703	79.75	570	-	-
SC+SoT	83.67	234	90.00	106	68.66	190	80.00	135	91.33	111	62.00	187	79.28	161	71.80	-0.47
Qwen-2.5-7B
CoT	77.41	180	85.78	172	63.22	279	76.78	137	86.44	183	57.00	246	74.44	200	-	-
SoT	77.05	73	85.11	27	59.78	61	77.22	44	85.00	27	58.00	105	73.69	56	71.90	-0.74
SC+CoT	79.33	542	86.44	516	66.11	837	78.33	412	87.00	550	58.34	739	75.93	600	-	-
SC+SoT	78.83	219	85.66	81	60.34	184	77.33	134	85.00	82	59.00	317	74.36	169	71.90	-1.57

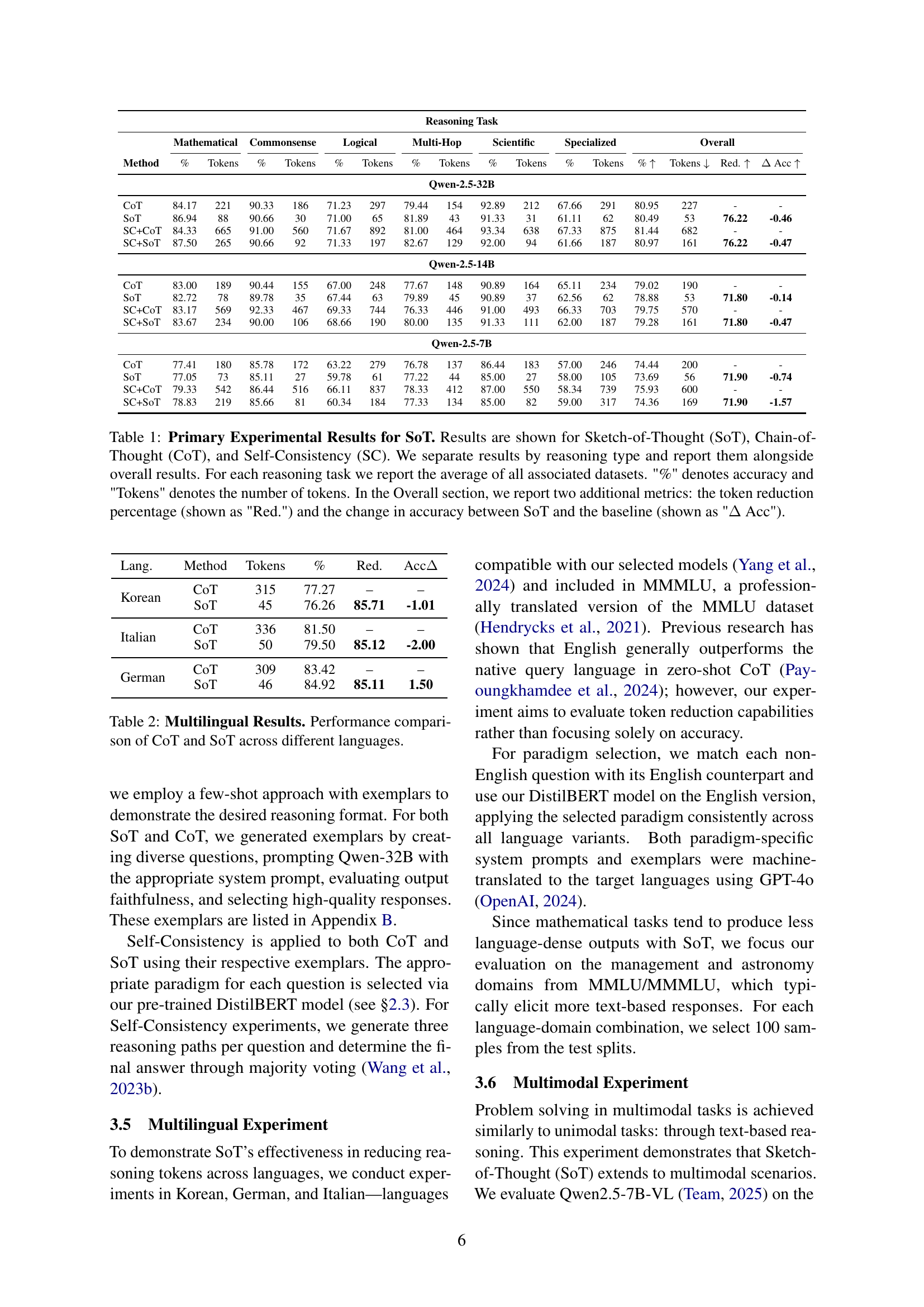
🔼 This table presents a comparison of the performance of three different prompting methods: Sketch-of-Thought (SoT), Chain-of-Thought (CoT), and Self-Consistency (SC) across 15 reasoning datasets. The results are categorized by reasoning type (Mathematical, Commonsense, Logical, Multi-hop, Scientific, Specialized) and show the average accuracy and number of tokens used for each method within each category. Overall performance metrics are also provided, including the percentage reduction in tokens achieved by SoT compared to CoT and the change in accuracy. The table is broken down by model size (7B, 14B, 32B parameters).
read the caption
Table 1: Primary Experimental Results for SoT. Results are shown for Sketch-of-Thought (SoT), Chain-of-Thought (CoT), and Self-Consistency (SC). We separate results by reasoning type and report them alongside overall results. For each reasoning task we report the average of all associated datasets. '%' denotes accuracy and 'Tokens' denotes the number of tokens. In the Overall section, we report two additional metrics: the token reduction percentage (shown as 'Red.') and the change in accuracy between SoT and the baseline (shown as 'ΔΔ\Deltaroman_Δ Acc').

In-depth insights
#

Cognitive Sketch
#

While the term “Cognitive Sketch” isn’t explicitly used in the document, the paper’s core concept, Sketch-of-Thought (SoT), strongly embodies it. SoT draws inspiration from cognitive science, specifically the idea of “sketches” as efficient intermediaries in cognitive processes. The paper emphasizes the use of symbolic representations, domain-specific notation, and abbreviation to distill reasoning steps. The goal is to minimize verbosity while preserving essential logical connections, mirroring how experts often approach problem-solving. The paper implements it using Conceptual Chaining, Chunked Symbolism, and Expert Lexicons, all acting as methods to create simplified cognitive representations. SoT is about finding the “sketch” which efficiently conveys the thought process.

Adaptive Routing
#

Adaptive routing, as presented, is a crucial component for the Sketch-of-Thought framework, intelligently selecting the most suitable reasoning paradigm for a given query. This dynamic approach is essential because different reasoning tasks benefit from different cognitive strategies, such as Conceptual Chaining, Chunked Symbolism, or Expert Lexicons. By analyzing question characteristics, like the presence of mathematical symbols or domain-specific terminology, the lightweight router model dynamically chooses the optimal strategy, maximizing efficiency and accuracy. This adaptability ensures that resources are allocated effectively, leveraging each paradigm’s strengths while minimizing its weaknesses. The goal is a seamless and efficient integration of cognitive science principles into language model reasoning, mirroring the nuanced decision-making processes of human experts. Adaptive routing improves token efficiency and maintains strong performance across diverse reasoning domains. It showcases a shift towards more context-aware AI.

Token Reduction
#

The paper introduces Sketch-of-Thought (SoT) as a method to substantially reduce token usage in LLMs during reasoning, addressing the verbosity issues of Chain-of-Thought (CoT). SoT aims for a 70-80% token reduction while maintaining or improving accuracy. They use cognitive-inspired paradigms and it could potentially lead to computational savings and improve practicality, especially in resource-constrained environments, democratizing AI access. This is achieved through structured, less verbose reasoning processes.

LLM Efficiency
#

LLM efficiency is a crucial research area, focusing on reducing computational costs and token usage. Sketch-of-Thought (SoT), for example, enhances efficiency by combining cognitive-inspired reasoning with linguistic constraints, yielding substantial token reductions while maintaining accuracy. Methods like concise chain-of-thought aim to limit response length, and other strategies distill verbose reasoning into efficient forms. By structuring reasoning according to cognitive principles, models can focus on essential logical connections, leading to more efficient and cost-effective AI reasoning.

Multimodal SoT
#

Based on the provided research paper, ‘Multimodal SoT’ likely refers to the extension of Sketch-of-Thought (SoT) to scenarios involving both text and images. It seems the authors explore whether SoT, which reduces token usage by generating concise reasoning chains, can be effectively applied when the input includes visual information. The experiment with the multimodal split of ScienceQA suggests they aim to demonstrate that SoT can dramatically reduce verbosity while preserving performance even when reasoning requires visual and textual integration. This implies that the core principles of SoT – cognitive-inspired sketching, paradigm selection, and efficient knowledge representation – are generalizable and not limited to text-based reasoning. This is significant because real-world applications often involve processing information from multiple modalities. The potential for SoT to improve efficiency in multimodal reasoning could be crucial for deploying LLMs in resource-constrained environments where image processing is also computationally expensive. A key element is handling the image context, where it’s either ignored or implicitly represented in the paradigm selection process.

More visual insights
#

More on tables

Lang.	Method	Tokens	%	Red.	Acc $\Delta$
Korean	CoT	315	77.27	–	–
Korean	SoT	45	76.26	85.71	-1.01
Italian	CoT	336	81.50	–	–
Italian	SoT	50	79.50	85.12	-2.00
German	CoT	309	83.42	–	–
German	SoT	46	84.92	85.11	1.50

🔼 This table presents a comparison of the performance of Chain-of-Thought (CoT) and Sketch-of-Thought (SoT) prompting methods across three different languages: Korean, Italian, and German. For each language, the table shows the number of tokens used by both CoT and SoT, as well as their respective accuracy scores. This allows for a direct comparison of the efficiency and effectiveness of the two methods in multilingual contexts.
read the caption
Table 2: Multilingual Results. Performance comparison of CoT and SoT across different languages.

Method	Tokens	%	Red	Acc $\Delta$
CoT	151	85.91	–	–
SoT	28	82.47	81.46	-3.44

🔼 This table presents a comparison of the performance of Chain-of-Thought (CoT) and Sketch-of-Thought (SoT) prompting methods on multimodal reasoning tasks using the Qwen-2.5-VL 7B model. It shows the number of tokens generated, the accuracy achieved, the percentage reduction in tokens achieved by SoT compared to CoT, and the difference in accuracy between the two methods. The results demonstrate SoT’s efficiency in reducing token usage while maintaining comparable accuracy to CoT in multimodal scenarios.
read the caption
Table 3: Multimodal Results. Performance comparison of CoT and SoT for multimodal reasoning tasks.

Dataset	Citation	HF ID
GSM8K	Cobbe et al. (2021)	gsm8k
SVAMP	Patel et al. (2021)	ChilleD/SVAMP
AQUA-RAT	Ling et al. (2017)	aqua_rat
DROP	Dua et al. (2019)	drop
OpenbookQA	Mihaylov et al. (2018)	openbookqa
StrategyQA	Geva et al. (2021)	ChilleD/StrategyQA
LogiQA	Liu et al. (2020)	lucasmccabe/logiqa
Reclor	Yu et al. (2020)	metaeval/reclor
HotPotQA	Yang et al. (2018)	hotpot_qa
MuSiQue-Ans	Trivedi et al. (2022)	dgslibisey/MuSiQue
QASC	Khot et al. (2020)	allenai/qasc
Worldtree	Jansen et al. (2018)	nguyen-brat/worldtree
PubMedQA	Jin et al. (2019)	qiaojin/PubMedQA
MedQA	Jin et al. (2020)	bigbio/med_qa
MMLU	Hendrycks et al. (2021)	cais/mmlu
MMMLU	Hendrycks et al. (2021)	openai/MMMLU
ScienceQA	Lu et al. (2022)	lmms-lab/ScienceQA

🔼 This table lists the fifteen datasets used in the paper’s experiments. For each dataset, it provides the dataset’s full citation and its corresponding Hugging Face ID, a unique identifier used to easily access the dataset’s data within the Hugging Face ecosystem. This allows for reproducibility and facilitates access for other researchers.
read the caption
Table 4: Dataset Information. Details of datasets used for evaluation including their citation and Hugging Face ID.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Cognitive Sketch#

Adaptive Routing#

Token Reduction#

LLM Efficiency#

Multimodal SoT#

More visual insights#

Full paper#