TL;DR#
Time series models face challenges in scaling to handle large and complex datasets, requiring innovative approaches. While researchers have explored various architectures like Transformers, LSTMs, and GRUs, the unique characteristics of time series data and the computational demands of model scaling necessitate new solutions. Current methods often struggle with heightened computational demands and potential accuracy losses when processing data.
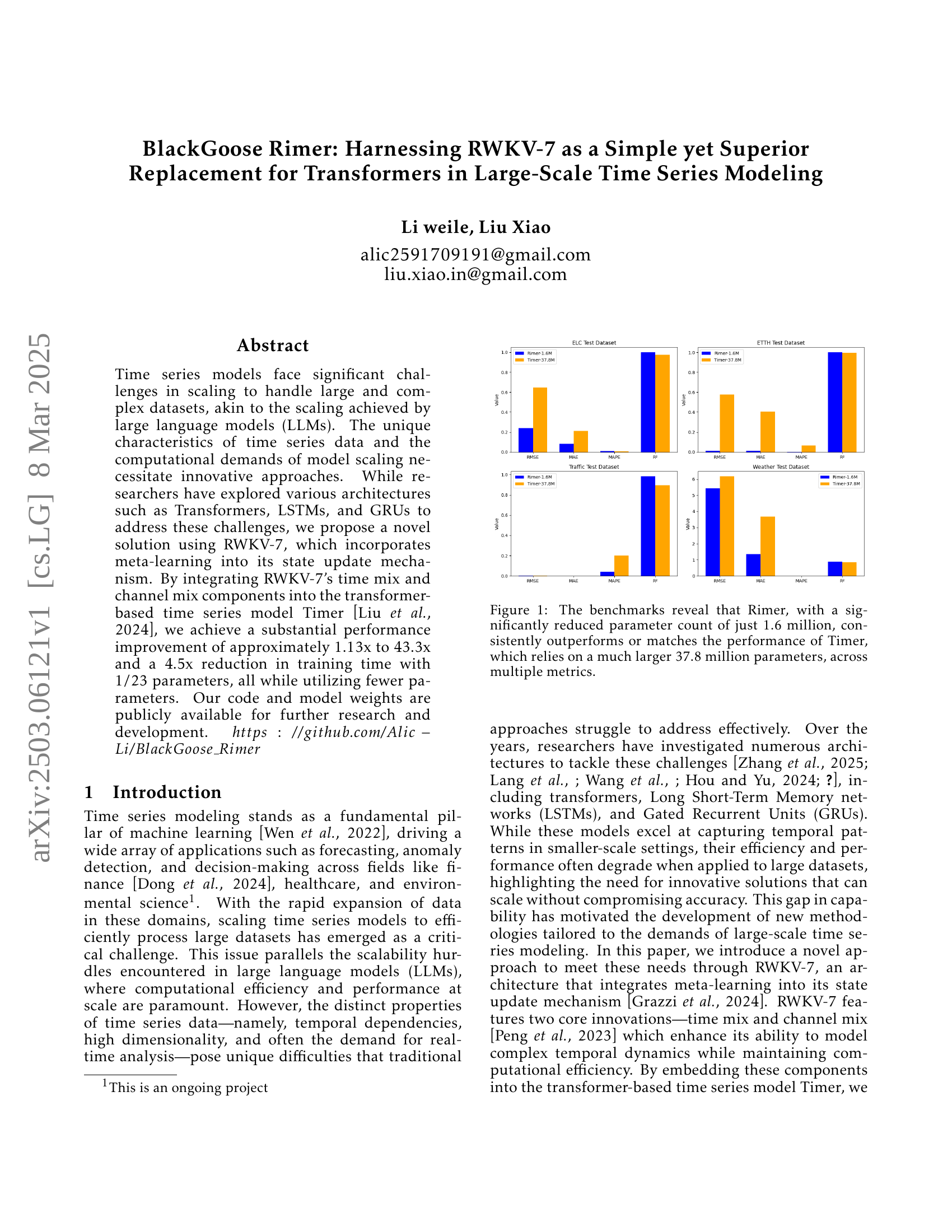
The paper introduces Rimer, a novel solution using RWKV-7, which incorporates meta-learning. By integrating RWKV-7’s time mix and channel mix into Timer (a transformer-based time series model), Rimer achieves substantial performance improvements and reduces training time with fewer parameters. Benchmarks reveal that Rimer matches or outperforms Timer across metrics, offering a lightweight solution for scaling time series models.
Key Takeaways#
Why does it matter?#
This paper introduces a novel approach to time series modeling, achieving significant performance improvements with fewer parameters. It offers a lightweight, scalable solution that addresses the challenges of big data in various real-world applications, opening avenues for efficient and accurate time series analysis.
Visual Insights#

🔼 The bar chart compares the performance of two time series models, Rimer and Timer, across four datasets (ELC, ETTH, Traffic, and Weather). Rimer, despite having significantly fewer parameters (1.6 million vs. Timer’s 37.8 million), demonstrates comparable or superior performance across multiple evaluation metrics (RMSE, MAE, MAPE, and R2). This highlights Rimer’s efficiency and effectiveness in large-scale time series modeling.
read the caption
Figure 1: The benchmarks reveal that Rimer, with a significantly reduced parameter count of just 1.6 million, consistently outperforms or matches the performance of Timer, which relies on a much larger 37.8 million parameters, across multiple metrics.
| RMSE | MAE | MAPE | ||
|---|---|---|---|---|
| Timer-37.8M | 0.6488 | 0.2127 | 0.61% | 0.9755 |
| Rimer-1.6M | 0.2409 | 0.0814 | 0.81% | 0.9991 |
🔼 This table presents a comparison of the performance of the Rimer-1.6M and Timer-37.8M models on the ELC dataset. It shows the Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and R-squared (R²) values for both models. The metrics assess the accuracy of each model’s predictions on the dataset, with lower RMSE, MAE, and MAPE indicating better performance. R² is a measure of the goodness of fit, with a value closer to 1 implying a stronger correlation between the predicted and actual values. The table highlights the performance difference between a smaller, more efficient model (Rimer) and a larger, more traditional model (Timer).
read the caption
Table 1: ECL
In-depth insights#
RWKV-7 for TS#
RWKV-7’s potential in time series modeling (TS) is significant. It could offer a compelling alternative to Transformers, especially when resources are constrained. Its RNN architecture might capture temporal dependencies effectively, addressing challenges of scaling to large datasets, a known limitation of traditional RNNs. The RWKV-7 architecture with its time mix and channel mix components could enhance model capacity. RWKV-7 introduces meta-learning to improve the model’s ability to adapt to new time series tasks. The potential benefits of RWKV-7 for TS include improved accuracy, efficiency, and scalability, making it a valuable area for further research, given time series unique challenges in temporal dependencies, dimensionality, and real-time processing.
Meta-learning RNNs#
Meta-learning in Recurrent Neural Networks (RNNs) presents a compelling approach to enhance their adaptability and performance across diverse time-series tasks. The core idea revolves around enabling RNNs to learn how to learn, allowing them to quickly adapt to new datasets or tasks with minimal retraining. This is particularly valuable in scenarios where data is scarce or rapidly changing. By leveraging meta-learning techniques, RNNs can learn from a distribution of tasks, acquiring generalizable knowledge that facilitates efficient adaptation to unseen tasks. This can involve learning optimal initial parameters, learning how to update parameters, or learning task-specific architectures. The potential benefits include improved generalization, faster adaptation, and reduced computational costs. However, challenges remain, such as designing effective meta-learning algorithms for RNNs, addressing the computational complexity of meta-learning, and ensuring the stability of the learning process. Future research directions could explore incorporating attention mechanisms, memory networks, or hierarchical structures to further enhance the capabilities of meta-learning RNNs.
Test time scaling#
Test time scaling refers to the challenge of efficiently applying a trained time series model to new, unseen data, especially as the data volume and complexity increase. Traditional models often struggle with maintaining accuracy and speed when processing longer sequences, higher-frequency data, or additional features during testing. Addressing this challenge is crucial for real-world applications, where timely and accurate predictions are essential. Adaptive computational techniques are necessary to balance performance and efficiency, ensuring that the model can scale effectively without compromising its predictive capabilities. Novel frameworks that leverage insights gained from prior tasks can minimize retraining efforts, employing techniques such as few-shot learning and transfer learning, to generalize effectively across various scenarios. This boosts versatility and scalability, tackling challenges and paving the way for practical time series modeling solutions.
Implicit Layers#
Implicit layers, as employed within the RWKV-7 architecture, represent a paradigm shift by defining layer outputs as fixed-point solutions. This approach, inspired by Deep Equilibrium Models (DEQs), circumvents traditional sequential updates, offering potential benefits for recurrent networks. Instead of explicitly calculating a layer’s output based on the previous state, it finds the equilibrium point of a function, effectively creating an “infinite-depth” behavior without unrolling. This is particularly relevant for handling long-range dependencies, which would be great for time series data. The introduction of a self-recurrent term allows maintaining core dynamics. This implicit formulation allows using latent-space iterations, which can greatly improve expressive and efficiency. The key advantage lies in avoiding the computational cost associated with iterative unrolling, potentially enabling more efficient training and inference, especially when dealing with lengthy time series sequences.
Hybrid Models#
Hybrid models, particularly in time series analysis, represent a powerful paradigm shift, blending the strengths of distinct architectures to overcome individual limitations. The fusion of RWKV-7 with other models, such as Transformers or CNNs, can potentially lead to improved performance. RWKV-7 excels in sequence modeling, while Transformers offer efficient parallel processing and global context awareness, and CNNs are adept at extracting local patterns. Combining them can capture both short and long-term dependencies effectively. This hybridization allows for nuanced modeling, where each component addresses specific aspects of the data, resulting in enhanced predictive accuracy and robustness. The exploration of such architectures promises significant advancements in addressing complex, real-world time series challenges. Specifically, these allow researchers to use models in a way that reduces resource constraints and provides the versatility needed for efficient modeling.
More visual insights#
More on tables
| RMSE | MAE | MAPE | ||
|---|---|---|---|---|
| Timer-37.8M | 0.5770 | 0.4050 | 6.5% | 0.9968 |
| Rimer-1.6M | 0.0133 | 0.0112 | 0.16% | 0.9998 |
🔼 Table 2 presents the evaluation results of the Rimer-1.6M and Timer-37.8M models on the ETTH (Electricity Transformer Hourly) dataset. It shows a comparison of the RMSE (Root Mean Squared Error), MAE (Mean Absolute Error), MAPE (Mean Absolute Percentage Error), and R² (R-squared) metrics for both models. These metrics quantify the performance of the models in forecasting electricity transformer hourly data. The table highlights the significant performance improvement achieved by the more parameter-efficient Rimer model.
read the caption
Table 2: ETTH
| RMSE | MAE | MAPE | ||
|---|---|---|---|---|
| Timer-37.8M | 0.0055 | 0.0015 | 19.94% | 0.8955 |
| Rimer-1.6M | 0.0025 | 0.0006 | 4.01% | 0.9838 |
🔼 This table presents the evaluation results of the Rimer-1.6M and Timer-37.8M models on the Traffic dataset. It shows the performance metrics RMSE (Root Mean Squared Error), MAE (Mean Absolute Error), MAPE (Mean Absolute Percentage Error), and R-squared (R²) for both models. These metrics assess the accuracy of the models in predicting traffic data.
read the caption
Table 3: Traffic
| RMSE | MAE | MAPE | ||
|---|---|---|---|---|
| Timer-37.8M | 6.1765 | 3.6839 | 0.88% | 0.8411 |
| Rimer-1.6M | 5.4311 | 1.3621 | 0.34% | 0.8794 |
🔼 This table presents the performance comparison between the Rimer-1.6M and Timer-37.8M models on the Weather dataset. It shows the Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and R-squared (R²) values for both models, highlighting the significant performance improvement and parameter efficiency achieved by Rimer-1.6M.
read the caption
Table 4: Weather
Full paper#