Mixture of Experts Made Intrinsically Interpretable

2503.07639

Xingyi Yang et el.

🤗 2025-03-12

TL;DR
#

Large language models excel, but their inner workings remain a mystery, leading to unpredictable behavior. Polysemanticity, where neurons encode multiple concepts, hinders interpretability. Post-hoc methods like Sparse Auto-Encoders (SAEs) are used, but these are costly and often incomplete. Instead, architectural changes can directly design interpretability into the model, but this is often done on toy tasks or comes at a compromise.

To address this, the paper introduces MoE-X, a Mixture-of-Experts model designed for intrinsic interpretability. It leverages wider, sparser networks, made possible by MoE architectures, to capture interpretable factors. It is done by Rewriting the MoE layer as a sparse, large MLP while enforcing sparse activation within each expert, and routes based on activation sparsity. Evaluations shows MoE-X achieves both competitive performance and enhanced interpretability.

Key Takeaways
#

Why does it matter?
#

This research presents MoE-X, to build intrinsically interpretable models, potentially leading to more trustworthy and understandable AI systems. The method is relevant to current trends in mechanistic interpretability and opens avenues for investigating sparse architectures and routing mechanisms.

Visual Insights
#

🔼 This figure illustrates the MoE-X architecture, highlighting its design for interpretability. MoE-X addresses the challenge of polysemantic neurons in large language models by creating a wider network with sparse activations. Unlike standard MLPs which have dense connections and activations, MoE-X employs multiple smaller MLPs (’experts’) that are only activated for a subset of input tokens. Crucially, MoE-X enforces sparsity within each expert and uses a sparsity-aware routing mechanism. This mechanism prioritizes sending tokens to experts producing the sparsest activations. This design encourages more disentangled feature representations within the network, which contributes to better interpretability. The figure contrasts MoE-X with traditional dense and wide MLPs, showcasing MoE-X’s unique combination of width and controlled sparsity.
read the caption
Figure 1: MoE-X introduces a sparse and wide network architecture designed for interpretability. Compared to dense MLPs, it incorporates both sparsity and a wider structure. Unlike traditional MoE models, it enforces sparsity within each expert and routes tokens to the sparsest experts.

Activation Function
Model	Val Loss $\downarrow$	Coverage $\uparrow$	Reconstruction $\uparrow$
GELU (GPT-2)	0.213	0.356	0.608
ReLU	0.215	0.312	0.581
GEGLU	0.209	0.255	0.394
SoLU	0.216	0.306	0.343
Mixture-of-Experts
Monet-HD	0.210	0.312	0.528
Monet-VD	0.212	0.283	0.482
PEER	0.214	0.323	0.426
Switch	0.212	0.424	0.734
MoE-X	0.211	0.428	0.840

🔼 This table compares the performance and interpretability of different model architectures on a chess dataset. The key characteristic is that all models have the same number of activated parameters. This allows for a direct comparison of the impact of architectural choices (e.g., activation function, mixture-of-experts design) on both performance (measured by validation loss) and interpretability (measured by BSP Coverage and Reconstruction scores). The baseline is a standard GPT-2 model, and it is compared against models using various activation functions and mixture-of-experts architectures. Higher scores in the Coverage and Reconstruction columns indicate better interpretability.
read the caption
Table 1: Comparison with baseline method by keeping model activated parameters the same.

In-depth insights
#

MoE: Intrinsically
#

The concept of making Mixture of Experts (MoE) intrinsically interpretable is fascinating. Current MLPs neurons are polysemantic. The MoE route-based mechanism can be designed to prioritize only salient features, thus creating sparse wide network. This approach ensures that the most relevant features are processed by the experts. Sparsity is achieved by ReLU activation and sparsity-aware routing. Post-hoc interpretability methods like sparse autoencoders (SAEs) are computationally expensive. Therefore, intrinsicality is achieved by designing interpretability directly into the model architecture to discourage polysemanticity during training.

Sparsity & Width
#

Sparsity and width are crucial architectural elements in neural networks, influencing both performance and interpretability. Width, referring to the number of neurons in a layer, provides capacity for the network to learn complex patterns. Increasing width allows the model to represent more diverse features and potentially reduces feature superposition. Sparsity, achieved through mechanisms like ReLU activation or k-sparse layers, encourages only a subset of neurons to be active for any given input. This reduces interference between features, making the model’s internal representations more disentangled and interpretable. The interplay between sparsity and width is critical; a wide network with controlled sparsity can effectively allocate distinct neurons to specific features while minimizing redundancy and promoting clearer, more semantically meaningful representations.

ReLU Experts Rule
#

The name ‘ReLU Experts Rule’ implies the significant impact of using ReLU activation functions within a Mixture of Experts architecture. ReLU’s sparsity-inducing property likely leads to more disentangled representations, addressing polysemanticity. This sparsity, inherent to ReLU, allows each expert to specialize on a narrower set of features. The ‘rule’ suggests that ReLU’s effect on interpretability outweighs any potential drawbacks. Efficient scaling and enhanced feature disentanglement contribute significantly to model transparency, highlighting the practical advantages of this design choice.

Chess LLM: Truth
#

While “Chess LLM: Truth” isn’t present, the paper extensively utilizes chess as a testing ground. Chess provides a controlled environment to evaluate interpretability. Since chess has definitive rules, a chess LLM’s internal representations are objectively verifiable against the ground truth of board states and optimal moves. The work here demonstrates a clear path for creating LLMs that are aligned with the internal representations to outside world. It avoids LLM from hallucinating factors because the objective truth is available in the outside world. This concept should be applied to other area, which has clear rule-based setting, to make LLM more interpretable.

Routing Matters
#

Routing is critical, and this paper appears to highlight the need for routing mechanisms that go beyond simple load balancing. Effective routing is tightly coupled with the model’s overall goal; the routing must consider interpretability rather than just performance. A carefully designed routing system, which considers sparsity, can facilitate the emergence of disentangled representations. A routing mechanism that simply distributes tokens to experts without considering their relevance to the input or the desired output could actually hinder interpretability. The paper’s emphasis on sparsity-aware routing suggests that a routing function must prioritize experts whose activations best reflect the salient features of the input, leading to a more understandable and meaningful representation. This requires innovations in how routing decisions are made, potentially involving approximations or heuristics to maintain computational efficiency while still promoting interpretability.

More visual insights
#

More on figures

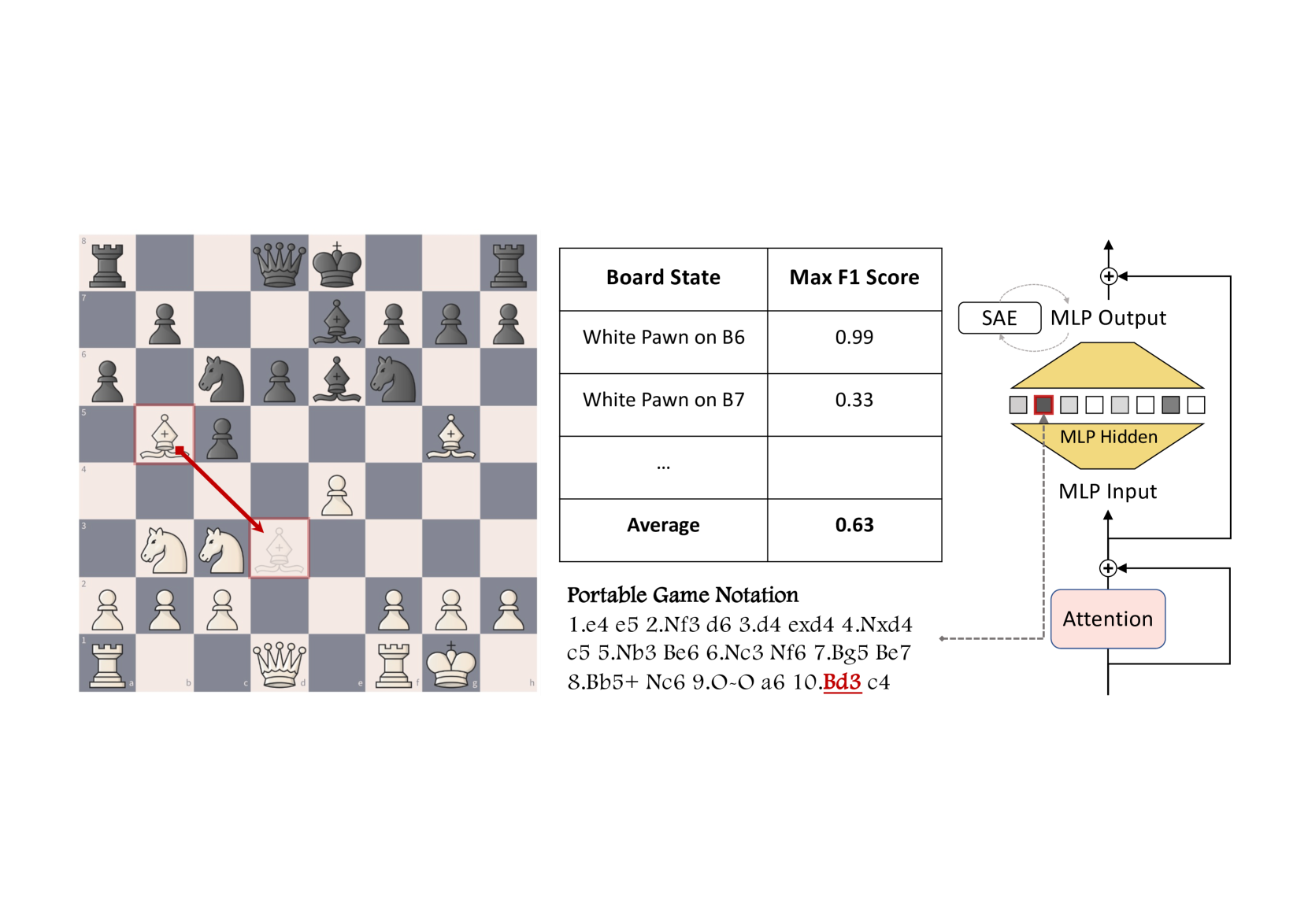
🔼 This figure illustrates the methodology used to evaluate the interpretability of a large language model (LLM) in the context of chess games. The LLM processes a Portable Game Notation (PGN) string, a textual representation of a chess game. The model’s internal activations (from the Multi-Layer Perceptron, or MLP) are then analyzed to determine how well they align with semantically meaningful properties of the chess board state (BSP). The figure visually connects the input PGN string, the internal MLP hidden layer activations, and their relation to the BSP to show how the LLM processes and represents chess-relevant information. This process helps assess whether the LLM’s internal representations are aligned with the actual meaningful concepts of chess, allowing for an evaluation of the model’s interpretability.
read the caption
Figure 2: Illustration of using chess game to evaluate the LLM’s interpretability.

🔼 This figure displays the relationship between model size (in MB) and BSP (Board State Properties) Coverage score. Multiple lines represent different model configurations, varying the hidden size multiplier (α) and the input dimension (d) of the MLP (Multi-Layer Perceptron). The x-axis shows model size, and the y-axis shows the BSP Coverage score, a metric indicating the model’s ability to capture meaningful chessboard information. The graph allows for a visual comparison of how increasing model size, through adjustments in α and d, affects the model’s interpretability as measured by the coverage score. A baseline using Sparse Autoencoder (SAE) is also included for reference.
read the caption
Figure 3: Comparision BSP Coverage score v.s. the Model size.

🔼 This figure displays the results of an experiment evaluating the relationship between the sparsity of hidden layer activations and the interpretability of a language model trained on chess game data. The x-axis represents the L0 norm of hidden layer activations, which is a measure of sparsity (lower values indicate higher sparsity). The y-axis represents the BSP Coverage score, a metric for assessing interpretability in this specific context, where higher scores mean better interpretability. The plot shows multiple lines representing different model sizes, demonstrating how changes in model size affect the relationship between sparsity and interpretability. The goal of the experiment was to determine the optimal level of sparsity for achieving high interpretability.
read the caption
Figure 4: Comparing BSP Coverage score v.s. L𝐿Litalic_L-0 norm of the hidden.

🔼 This figure compares the performance of different models in terms of BSP Coverage and Reconstruction scores across varying model sizes. BSP Coverage represents how well the model’s internal activations align with semantically meaningful chess board state properties. Reconstruction score reflects how well the model can recover the complete state of a chessboard from its internal representations. The figure visually demonstrates the impact of model size and architectural choices (e.g., different activation functions and Mixture of Experts approaches) on the model’s ability to both capture interpretable chess features and reconstruct board states from those features.
read the caption
Figure 5: BSP Coverage and Reconstruction score of different model sizes.

🔼 This figure visualizes the encoder weights of different Mixture-of-Experts (MoE) models trained on a chess dataset using t-distributed Stochastic Neighbor Embedding (t-SNE). Each point represents an encoder weight vector. The different panels show the results for three model variants: a standard MoE, an MoE with ReLU activation functions in the expert networks, and a MoE incorporating all design choices of the proposed MoE-X architecture. The clustering of points reveals how the different architectural choices influence the structure of the latent space learned by the model. Specifically, it helps to show if features are disentangled across experts, aiding the interpretability of the model.
read the caption
Figure 6: t-SNE projections of encoder weights for original MoE layer, MoE with ReLU experts, and without full MoE-X layers, trained on Chess dataset.

🔼 This figure visualizes the results of an auto-interpretation experiment on the MoE-X small model, trained on the RedPajama-v2 validation dataset. It showcases several examples of activated tokens for different experts, along with their corresponding interpretations generated by the auto-interpretation process. The interpretations provide insights into the semantic meaning each expert is associated with.
read the caption
Figure 7: Activated tokens for experts in MoE-X small on RedPajama-v2 validation dataset. Their interpretations were identified using the auto-interpretation.

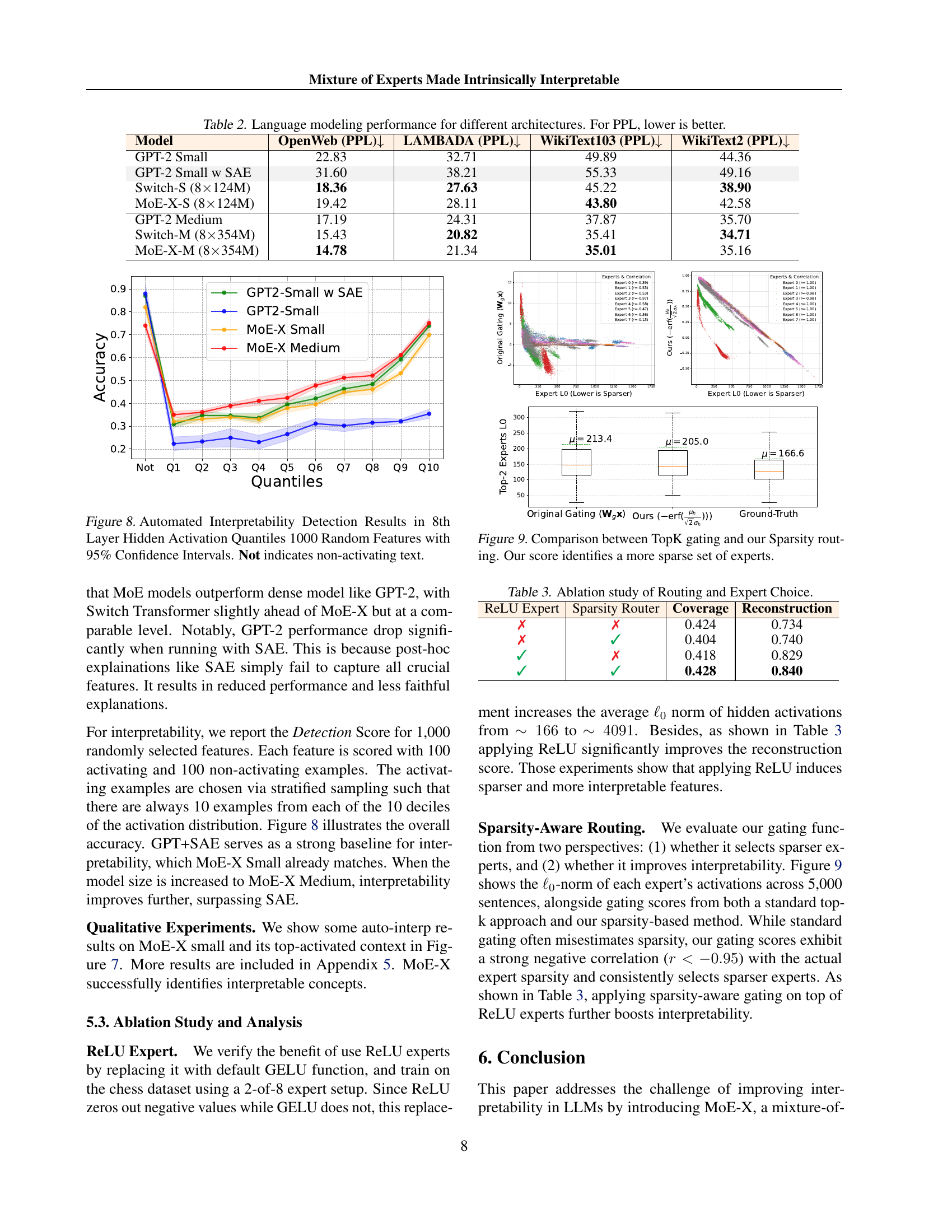
🔼 This figure displays the results of an automated interpretability detection experiment on the 8th layer of a hidden activation in a language model. The experiment used 1000 randomly selected features and calculated 95% confidence intervals for their accuracy. Each feature’s accuracy was measured using 100 activating and 100 non-activating text examples. The examples were chosen using stratified sampling to ensure a balanced representation across the activation distribution’s deciles. The ‘Not’ label indicates non-activating text.
read the caption
Figure 8: Automated Interpretability Detection Results in 8th Layer Hidden Activation Quantiles 1000 Random Features with 95% Confidence Intervals. Not indicates non-activating text.

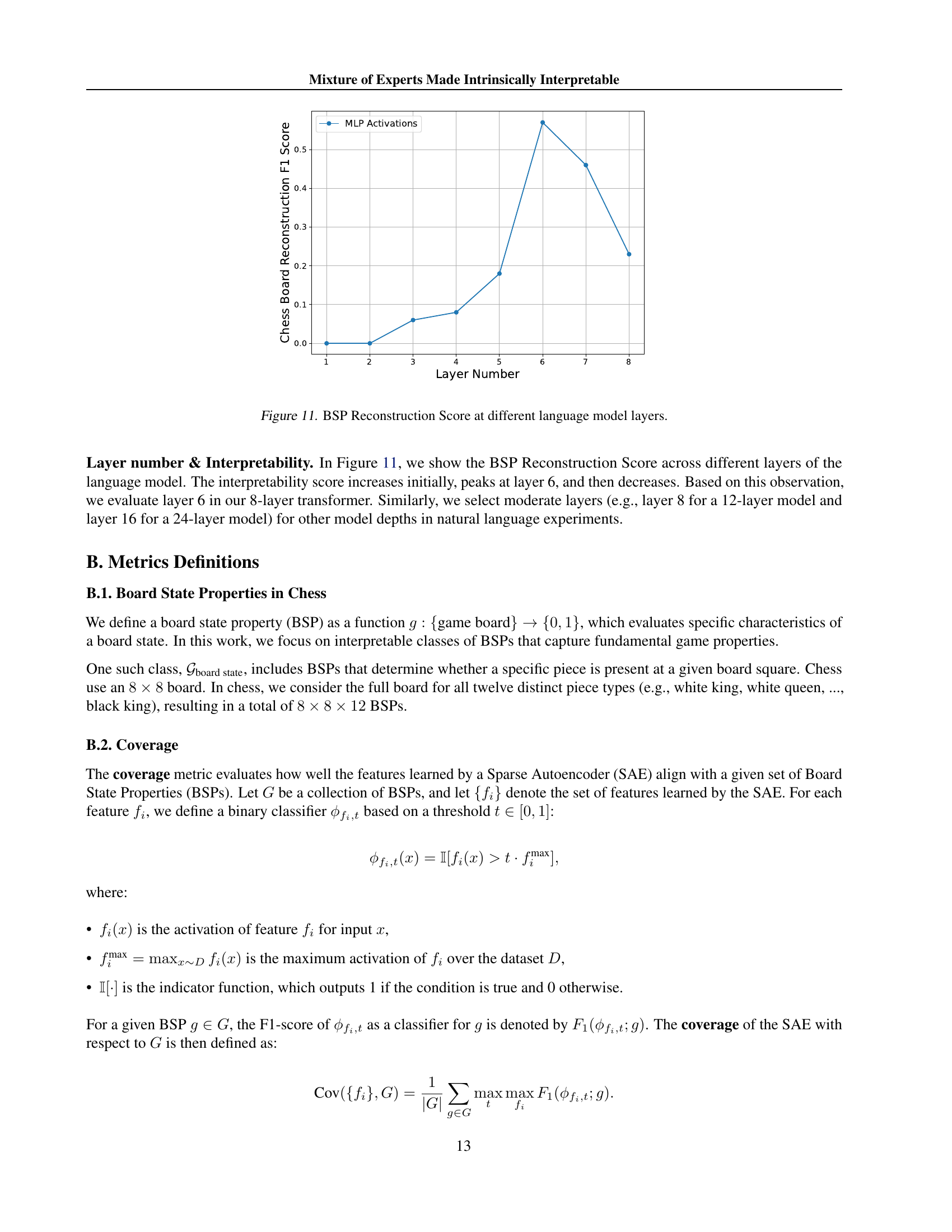
🔼 Figure 9 compares the performance of two gating mechanisms: the standard TopK gating and the proposed sparsity-aware routing method. Both methods aim to select experts for processing input tokens within a Mixture-of-Experts (MoE) architecture. The x-axis represents the L0 norm of the experts’ activation vectors (a measure of sparsity, where lower values indicate higher sparsity). The y-axis shows the value of the gating scores assigned to each expert by each method. The plot reveals that the TopK gating mechanism does not reliably select sparse experts. In contrast, the proposed sparsity-aware gating scores exhibit a strong negative correlation with the actual expert sparsity. The plot visually demonstrates that the new method significantly improves the selection of sparse experts.
read the caption
Figure 9: Comparison between TopK gating and our Sparsity routing. Our score identifies a more sparse set of experts.

More on tables

Model	OpenWeb (PPL) $\downarrow$	LAMBADA (PPL) $\downarrow$	WikiText103 (PPL) $\downarrow$	WikiText2 (PPL) $\downarrow$
GPT-2 Small	22.83	32.71	49.89	44.36
GPT-2 Small w SAE	31.60	38.21	55.33	49.16
Switch-S (8 $\times$ 124M)	18.36	27.63	45.22	38.90
MoE-X-S (8 $\times$ 124M)	19.42	28.11	43.80	42.58
GPT-2 Medium	17.19	24.31	37.87	35.70
Switch-M (8 $\times$ 354M)	15.43	20.82	35.41	34.71
MoE-X-M (8 $\times$ 354M)	14.78	21.34	35.01	35.16

🔼 This table presents the results of language modeling experiments using different model architectures. The models were evaluated on four standard natural language processing benchmarks: OpenWeb, LAMBADA, WikiText-103, and WikiText-2. The performance metric used is perplexity (PPL), where lower perplexity indicates better performance. The table compares the performance of GPT-2 (small and medium sizes), Switch Transformers (small and medium sizes), and MoE-X (small and medium sizes). The table also includes a GPT-2 small model combined with Sparse Autoencoders (SAE) for comparison. This comparison aims to show the performance trade-offs between dense models and sparse MoE models, highlighting the effect of architecture on model interpretability.
read the caption
Table 2: Language modeling performance for different architectures. For PPL, lower is better.

ReLU Expert	Sparsity Router	Coverage	Reconstruction
✗	✗	0.424	0.734
✗	✓	0.404	0.740
✓	✗	0.418	0.829
✓	✓	0.428	0.840

🔼 This table presents the results of ablation studies conducted to evaluate the impact of two key design choices in the MoE-X model on its performance and interpretability. Specifically, it examines the effects of using ReLU activation within experts and employing sparsity-aware routing, both individually and in combination. The table shows how these design choices affect the model’s ability to accurately reconstruct board states (Reconstruction) and capture semantically meaningful features of chess games (Coverage). The results highlight the importance of both design elements for achieving optimal performance in terms of interpretability.
read the caption
Table 3: Ablation study of Routing and Expert Choice.

Method	Coverage	Reconstruction
Dense	0.356	0.608
Dense (Continued Training)	0.377	0.674
MoE-X (Scratch)	0.398	0.657
MoE-X (Up-cycle)	0.428	0.840

🔼 This table compares the interpretability scores achieved by different training methods for a Mixture-of-Experts (MoE) model. The methods compared include training a dense model from scratch, continuing training of a dense model, training an MoE model from scratch, and training an MoE model using upcycled weights from a pre-trained dense model. The interpretability is measured using two metrics: BSP Coverage and Reconstruction score. Higher values for both metrics indicate better interpretability.
read the caption
Table 4: Comparison of interpretability scores for different training methods.

Auto-Interp Meaning	Location	Example
Time of day in expressions	Expert 2, #457	”We went for a walk in the evening.”
		”The meeting is scheduled for afternoon.”
		”She always exercises in the morning.”
Abbreviations with dots	Expert 5, #89	”She explained the concept using e.g. as an example.”
		”You must submit all forms by Friday, i.e., tomorrow.”
		”Common abbreviations include a.m. and p.m. for time.”
Capitals at the start of acronyms	Expert 6, #1601	”The NASA mission was successful.”
		”The company developed cutting-edge AI systems.”
		”Students use PDF documents for submissions.”
Ordinal numbers in sentences	Expert 3, #412	”He finished in 1st place.”
Hyphenated compound words	Expert 2, #187	”This is a well-being initiative.”
Currency symbols preceding numbers	Expert 1, #273	”The total cost was $100.”
Parentheses around numbers or letters	Expert 6, #91	”Refer to section (a) for details.”
Ellipsis usage	Expert 0, #55	”He paused and said, … I’ll think about it.”
Measurements followed by units	Expert 0, #384	”The box weighs 5 kg.”
Dates in numeric formats	Expert 7, #401	”The deadline is 2025-01-29.”
Repeated punctuation marks	Expert 2, #1128	”What is happening ???”
Hashtags in text	Expert 4, #340	”Follow the trend at #trending.”
Uppercase words for emphasis	Expert 4, #278	”The sign read, STOP immediately!”
Colon in timestamps	Expert 3, #521	”The train arrives at 12:30.”
Contractions with apostrophes	Expert 6, #189	”I can’t do this alone.”

🔼 This table displays examples of activated tokens and their corresponding contexts from the MoE-X Small model. The ‘Auto-interp process’ refers to an automated method used to interpret the meaning of the neuron activations. The table demonstrates how different neurons in the model respond to various linguistic features such as time expressions, abbreviations, capitalization, ordinal numbers, punctuation, and other aspects of text. Each row shows an example token, the associated neuron (Expert number and neuron ID), and a sample sentence showing the token in context.
read the caption
Table 5: Sampled Activated Tokens and Contexts for Neurons in MoE-X Small. The meanings are identified by the Auto-interp process.

Parameter	Value
Num layer	8
Num head	8
Num embd	512
dropout	0.0
Init learning rate	3e-4
Min lr	3e-5
Lr warmup iters	2000
Max iters	600000
optimizer	Adamw
batch size	100
context len	1023
Num experts	8
Num experts per Token	2
grad_clip	1.0

🔼 This table details the hyperparameters and training configuration used for training both the Mixture-of-Experts (MoE) and GPT-2 models on the chess dataset. It includes settings such as the number of layers, number of attention heads, embedding size, dropout rate, learning rate schedule, optimizer, batch size, and context length. It also specifies parameters specific to the MoE architecture, such as the number of experts and the number of experts activated per token. Understanding these settings is crucial for replicating the experimental results reported in the paper.
read the caption
Table 6: MoE & GPT-2 Training Configuration for Chess Dataset.

Names	Small	Medium
Num layer	12	24
Num head	12	16
Num embd	768	1024
dropout	0.0	0.0
Init learning rate	3e-4	3e-4
Min lr	3e-5	3e-5
Lr warmup iters	5000	5000
Max iters	100000	100000
optimizer	Adamw	Adamw
batch size	320	320
context len	1024	1024
Num experts	8	8
Num experts per Token	2	2
grad_clip	1.0	1.0

🔼 This table details the hyperparameters used for training small and medium sized MoE and GPT-2 models on the FineWeb language dataset. It lists the number of layers, heads, embedding dimensions, dropout rate, learning rate, learning rate warmup iterations, maximum iterations, optimizer, batch size, context length, number of experts, and the number of experts per token for each model configuration. The table provides a precise specification of the training settings used to compare the performance and interpretability of MoE-X against other models.
read the caption
Table 7: MoE & GPT-2 Small Training Configuration for FineWeb Language Tasks.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

MoE: Intrinsically#

Sparsity & Width#

ReLU Experts Rule#

Chess LLM: Truth#

Routing Matters#

More visual insights#

Full paper#