TL;DR#
Fitting a body to a 3D clothed human is a challenging task due to clothing variations and complex poses. Traditional methods struggle with pose initialization, while learning-based approaches lack generalization. Prior works use either registration or fitting approaches. Registration focuses on matching the outer surface, whereas fitting emphasizes aligning with the underlying body. However, existing methods don’t generalize well to varying poses, shapes, and clothing styles. Some approaches try to address this by separating the garment layers from the underlying body, but still, struggle with the out-of-distribution post or shapes.
This paper introduces ETCH, a novel pipeline that estimates cloth-to-body surface mapping through locally approximate SE(3) equivariance. It encodes tightness as displacement vectors from the cloth surface to the underlying body. Following this mapping, pose-invariant body features regress sparse body markers, simplifying clothed human fitting into an inner-body marker fitting task. Extensive experiments on CAPE and 4D-Dress show that ETCH significantly outperforms state-of-the-art methods in body fitting accuracy, both tightness-agnostic and tightness-aware.
Key Takeaways#
Why does it matter?#
ETCH provides a more accurate and generalizable way to fit 3D body models to clothed humans, improving pose and shape estimation. This improves applications like virtual try-on, motion capture, and biomechanics analysis, opening new research directions in human body understanding and animation.
Visual Insights#

🔼 Figure 1 showcases the effectiveness of the ETCH method in fitting 3D body meshes to clothed humans across various poses and clothing styles. The images display multiple examples where the algorithm accurately estimates the underlying body shape despite the presence of clothing. The ground truth body is represented in blue, the ETCH-fitted body in green, and ground truth markers are shown in black. The key innovation of ETCH, as highlighted in the caption, is the use of SE(3)-equivariant tightness vectors to model the cloth-to-body relationship, allowing for robust and accurate fitting even in challenging scenarios.
read the caption
Figure 1: Body Fitting on Clothed Humans. Given 3D clothed humans in any pose and clothing, ETCH accurately fits the body underneath. Our key novelty is modeling cloth-to-body SE(3)-equivariant \gradientRGBtightness vectors254,217,118192,50,26 for clothed humans, abbreviated as ETCH, which resembles “etching” from the outer clothing down to the inner body. The ground-truth body is shown in blue, our fitted body in green, and ground-truth markers as .
| Scan | GT body | NICP [41] | Ours | body-cloth |
🔼 This table presents a quantitative comparison of ETCH against state-of-the-art (SOTA) methods for 3D human body fitting from clothed scans. It shows the performance of ETCH and other methods (both tightness-agnostic and tightness-aware) on two datasets: CAPE and 4D-Dress. Evaluation metrics include vertex-to-vertex distance (V2V), mean per-joint position error (MPJPE), and Chamfer distance (CD). The table highlights ETCH’s superior performance, particularly its significant improvement over ArtEq in 4D-Dress MPJPE (approximately 32.6%). A note is included that NICP’s results in this table are without post-refinement, which is detailed in a later table.
read the caption
Table 1: Quantitative Comparison with SOTAs. ETCH clearly outperforms SOTAs, whether tightness-agnostic or -aware, in both CAPE and 4D-Dress across all metrics. In 4D-Dress-MPJPE, it surpasses the ArtEq by nearly 32.6%percent32.632.6\%32.6 %. Notably, for a fair comparison, no post-refinement is introduced to NICP [41] here, see NICP w/ post-refinement at Tab. 4.
In-depth insights#
Equivariant ETCH#
Based on the provided text, the core idea revolves around Equivariant Tightness Fitting for Clothed Humans (ETCH). The method uses the concept of SE(3) equivariance to model the relationship between a clothed human’s surface and their underlying body shape. Unlike previous methods that may struggle with generalization due to varied poses or garment types, ETCH aims to improve robustness by encoding tightness as displacement vectors that are locally SE(3) equivariant. This means that the learned relationship between the cloth and body remains consistent even as the body articulates or the clothing deforms. This approach combines strengths of both “equivariance” and “tightness”, the intention is to achieve robust body fitting. By explicitly modeling cloth-to-body interaction in an equivariant manner, the model should demonstrate stronger generalization across different poses, body shapes, and clothing styles, representing a significant advancement in the field.
Tightness Vectors#
The concept of Tightness Vectors represents a novel approach to modeling the relationship between a clothed human’s outer surface and the underlying body. Instead of relying on scalar values or binary tightness indicators, ETCH introduces displacement vectors that connect corresponding points on the cloth and body surfaces. This approach enables a more nuanced representation of clothing fit, capturing both the direction and magnitude of displacement. By learning these vectors, the model can effectively “etch” through the clothing to reveal the body shape underneath, regardless of garment type or pose. This is achieved through a framework leveraging SE(3) equivariance and invariant pointwise features allowing robustness in challenging situations.
Sparse Markers > Dense#
The comparison between sparse markers and dense correspondence reveals the strength of a sparse marker design. Mapping dense points to sparse markers and aggregating them with confidence creates a voting strategy that enhances robustness against low-confidence outliers. This is more effective than dense prediction, which can struggle with outliers and local minima. The paper’s method achieves significant improvements; This validates the use of sparse markers over dense correspondences. Incorrect dense correspondences can misguide optimization, leading to skewed body part rotations (e.g., hands, forearms, head), while the sparse marker strategy remains robust through its weighted voting mechanism.
OOD Generalization#
Out-of-Distribution (OOD) generalization is a crucial aspect of machine learning, particularly in the context of body fitting to clothed humans. It refers to the ability of a model to perform well on data that is different from the data it was trained on. This is especially important because real-world data often exhibits variations in pose, shape, clothing style, and dynamics that are not fully captured in training datasets. A model with strong OOD generalization can handle these variations and produce accurate body fits even for unseen poses, shapes, and clothing. The paper explores this by training the model on minimal data and evaluating its performance on the full validation set. Visualizations highlight how the proposed method maintains accurate inner body shape predictions and directional accuracy of the tightness vectors even with limited training data, demonstrating superior OOD generalization compared to methods lacking equivariant features. The use of equivariant features is key to OOD, as these features are designed to be invariant to certain transformations, such as rotations and translations, which helps the model generalize to new poses and viewpoints.
Limited Input Data#
The challenge of limited input data is a critical concern in machine learning, particularly when dealing with complex tasks like 3D human body fitting. The success of deep learning models heavily relies on the availability of large, diverse, and accurately labeled datasets. Insufficient data can lead to overfitting, where the model learns the training data too well and fails to generalize to new, unseen examples. This is especially problematic when dealing with variations in body shapes, poses, clothing styles, and dynamics. Data augmentation techniques can help to mitigate this issue by artificially expanding the dataset, but these methods may not fully capture the true complexity of the data distribution. Transfer learning, where knowledge gained from a related task is applied to the target task, can also be beneficial. Furthermore, developing models that are more data-efficient and can learn from smaller datasets is an active area of research.
More visual insights#
More on figures

🔼 Figure 2 illustrates the core difference between surface registration and body fitting in the context of 3D clothed humans. Surface registration techniques, exemplified by NICP [41], primarily focus on aligning the outer surface of the clothing with a template mesh. This approach is sensitive to clothing variations as the outer clothing shape influences the final registration. In contrast, body fitting methods prioritize aligning the underlying body shape with the template, resulting in a more robust solution that is less affected by diverse clothing styles and poses. The figure visually demonstrates the results of both approaches, highlighting the improved accuracy and robustness of body fitting.
read the caption
Figure 2: Registration vs. Fitting. Though both registration and fitting involve placing body inside clothing, “registration”, like NICP [41], focuses on matching the outer surface, whereas “fitting” emphasizes aligning with the underlying body, making it more robust to clothing variations.

🔼 Figure 3 illustrates the key components used for preparing the data to train the ETCH model. It shows how the model learns to map the outer surface of clothing to the underlying body. The figure highlights three key elements: 1) Tightness Vectors (V): These vectors connect points on the outer clothing surface to corresponding points on the underlying body surface, representing the displacement caused by the clothing. The magnitude of these vectors encodes how tightly the garment fits the body. 2) Marker-based Labels (L): These labels assign each point on the inner body surface to one of a set of predefined sparse markers on the body. These markers act as reference points for the body’s shape. 3) Confidence (C): This value represents the uncertainty or confidence associated with the tightness vector for each point. A confidence bar visually represents the geodesic distance (shortest path along the surface) from the point on the inner body to the nearest sparse marker, indicating the level of certainty in the mapping.
read the caption
Figure 3: Terminology of Tightness-Vector and Marker-Confidence. We illustrate the key components used for data preparation: 1) Tightness Vectors 𝐕𝐕\mathbf{V}bold_V, which connect the outer surface points with underneath body, and transmitting 2) Marker-based Labels 𝐋𝐋\mathbf{L}bold_L and Confidence 𝐂𝐂\mathbf{C}bold_C. We also provide a 2D illustration that unifies these terms together. Sparse markers as , and \gradientRGBconfidence bar242,171,8105,41,100 indicates the geodesic distance to the closest marker.

🔼 This figure illustrates the difference between articulated SO(3) equivariance, used in methods like ArtEq, and the local SO(3) equivariance used in ETCH. In articulated SO(3) equivariance, a rigid transformation (denoted by (\mathcal{T})) is applied to a body part, resulting in a consistent transformation of its features. In contrast, ETCH’s local SO(3) equivariance focuses on the tightness vector, which reflects the relationship between cloth and body. The tightness vector’s direction changes when the pose changes, but its overall behavior is similar due to its approximate equivariance, rather than a precise rigid transformation. The rainbow circle represents the feature vector (\mathcal{F}(\mathbf{X})) showing the multi-dimensional features extracted from the point cloud.
read the caption
Figure 4: SO(3) Equivariant Pose vs. Tightness. Rainbow circle is the feature ℱ(𝐗)ℱ𝐗\mathcal{F}(\mathbf{X})caligraphic_F ( bold_X ), for articulated SO(3)-equiv, 𝒯𝒯\mathcal{T}caligraphic_T denotes approximate rigid transformation of body part, while for our case, where the clothing roughly deforms with human poses, it refers to the tightness vector rotation.
More on tables
| Tightness Vector | Marker-based Labels | Geodesic-based Confidence | Unified 2D Illustration |
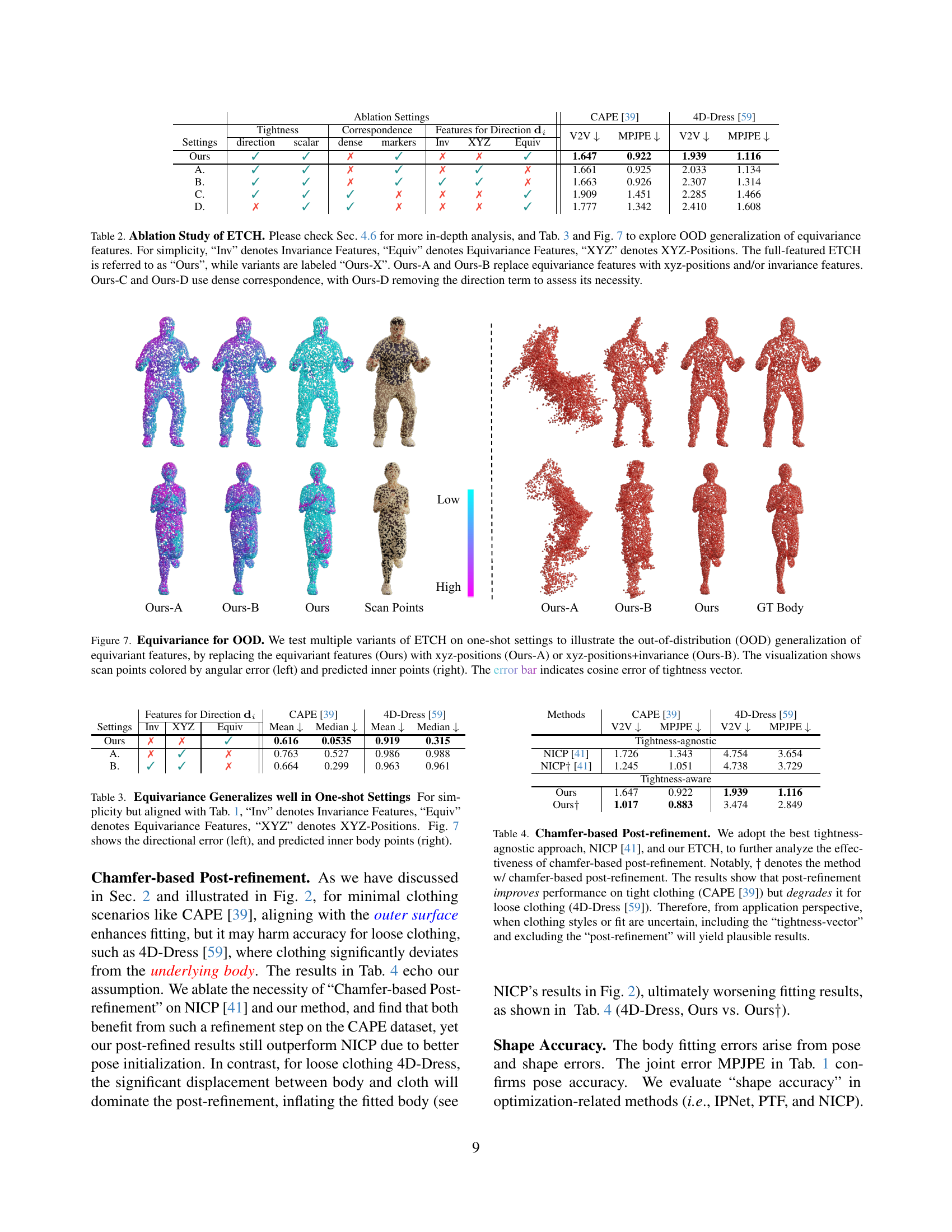
🔼 This table presents an ablation study on the Equivariant Tightness Fitting for Clothed Humans (ETCH) method. It compares the performance of the full ETCH model against several variants. These variants systematically remove or replace components of ETCH to isolate the effect of specific design choices. The components analyzed include: the use of equivariant features versus simple XYZ coordinates, the use of invariance features, the choice between sparse and dense marker correspondence, and the inclusion of the direction term in the tightness vector. The results are presented in terms of metrics such as vertex-to-vertex distance (V2V), mean per joint position error (MPJPE), and bidirectional Chamfer distance (CD), for both the CAPE and 4D-Dress datasets. The table allows readers to quantitatively assess the contribution of each component to ETCH’s overall performance.
read the caption
Table 2: Ablation Study of ETCH. Please check Sec. 4.6 for more in-depth analysis, and Tabs. 3 and 7 to explore OOD generalization of equivariance features. For simplicity, “Inv” denotes Invariance Features, “Equiv” denotes Equivariance Features, “XYZ” denotes XYZ-Positions. The full-featured ETCH is referred to as “Ours”, while variants are labeled “Ours-X”. Ours-A and Ours-B replace equivariance features with xyz-positions and/or invariance features. Ours-C and Ours-D use dense correspondence, with Ours-D removing the direction term to assess its necessity.
| Methods | CAPE [39] | 4D-Dress [59] | ||||
|---|---|---|---|---|---|---|
| V2V | MPJPE | CD | V2V | MPJPE | CD | |
| Tightness-agnostic | ||||||
| NICP [41] | 1.726 | 1.343 | - | 4.754 | 3.654 | - |
| ArtEq [22] | 2.200 | 1.557 | - | 2.328 | 1.657 | - |
| Tightness-aware | ||||||
| IPNet [7] | 2.593 | 1.917 | 1.110 | 3.826 | 2.625 | 1.262 |
| PTF [58] | 2.036 | 1.497 | 1.219 | 2.796 | 2.053 | 1.239 |
| Ours | 1.647 | 0.922 | 1.019 | 1.939 | 1.116 | 1.065 |
🔼 Table 3 presents an ablation study on the impact of using equivariant features in the ETCH model, specifically focusing on its generalization capabilities in one-shot settings (i.e., with minimal training data). It compares the performance of three variants of the model: one using equivariant features, one using only XYZ position information, and one using both XYZ positions and invariance features. The results are evaluated using mean and median angular errors in predicting the direction of tightness vectors, and the visualizations in Figure 7 show the directional error and the predicted inner body points for each model. The table aims to demonstrate the significant advantage of using equivariant features for robust direction prediction, especially when training data is scarce.
read the caption
Table 3: Equivariance Generalizes well in One-shot Settings For simplicity but aligned with Tab. 1, “Inv” denotes Invariance Features, “Equiv” denotes Equivariance Features, “XYZ” denotes XYZ-Positions. Fig. 7 shows the directional error (left), and predicted inner body points (right).
| Ablation Settings | CAPE [39] | 4D-Dress [59] | |||||||||
| Tightness | Correspondence | Features for Direction | V2V | MPJPE | V2V | MPJPE | |||||
| Settings | direction | scalar | dense | markers | Inv | XYZ | Equiv | ||||
| Ours | ✓ | ✓ | ✗ | ✓ | ✗ | ✗ | ✓ | 1.647 | 0.922 | 1.939 | 1.116 |
| A. | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ | ✗ | 1.661 | 0.925 | 2.033 | 1.134 |
| B. | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ | 1.663 | 0.926 | 2.307 | 1.314 |
| C. | ✓ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | 1.909 | 1.451 | 2.285 | 1.466 |
| D. | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ | 1.777 | 1.342 | 2.410 | 1.608 |
🔼 Table 4 shows the results of an ablation study comparing the performance of the proposed ETCH method with and without chamfer-based post-refinement. The study uses two datasets: CAPE (tight-fitting clothing) and 4D-Dress (loose clothing). The results demonstrate that chamfer-based post-refinement improves the accuracy of body fitting on the CAPE dataset, which has tighter-fitting clothing. However, on the 4D-Dress dataset, which contains loose clothing, post-refinement actually degrades performance. This suggests that the benefit of post-refinement is highly dependent on the style and fit of the clothing. For applications where clothing style and fit are uncertain, the authors recommend using the ETCH method without post-refinement for more reliable results. The table helps illustrate the importance of the novel tightness-vector approach in handling varying clothing styles and fits.
read the caption
Table 4: Chamfer-based Post-refinement. We adopt the best tightness-agnostic approach, NICP [41], and our ETCH, to further analyze the effectiveness of chamfer-based post-refinement. Notably, ††\dagger† denotes the method w/ chamfer-based post-refinement. The results show that post-refinement improves performance on tight clothing (CAPE [39]) but degrades it for loose clothing (4D-Dress [59]). Therefore, from application perspective, when clothing styles or fit are uncertain, including the “tightness-vector” and excluding the “post-refinement” will yield plausible results.
Full paper#