TL;DR#
Large language models (LLMs) often make mistakes in complex reasoning tasks. Existing methods like Process Reward Models(PRMs) requires large datasets and retraining. Also, training-free methods like majority voting or debate-based approaches have limitations such as failing in mathematical process error identification tasks. Therefore, a simple and effective training-free approach is needed to enhance process error identification capabilities.
To address the limitations, the paper introduces Temporal Consistency, a test-time method where LLMs iteratively refine judgments based on previous assessments. By leveraging consistency in self-reflection, it improves verification accuracy. Empirical evaluations on benchmarks like Mathcheck, ProcessBench, and PRM800K demonstrate consistent performance improvements over baselines. Results shows enabling 7B/8B distilled models outperform all 70B/72B models and GPT-40 on ProcessBench.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel test-time scaling method that improves the reliability of LLMs. The approach has potential to be integrated into existing systems and contribute to a more robust and trustworthy utilization of LLMs, inspiring new methods in reasoning and verification process.
Visual Insights#
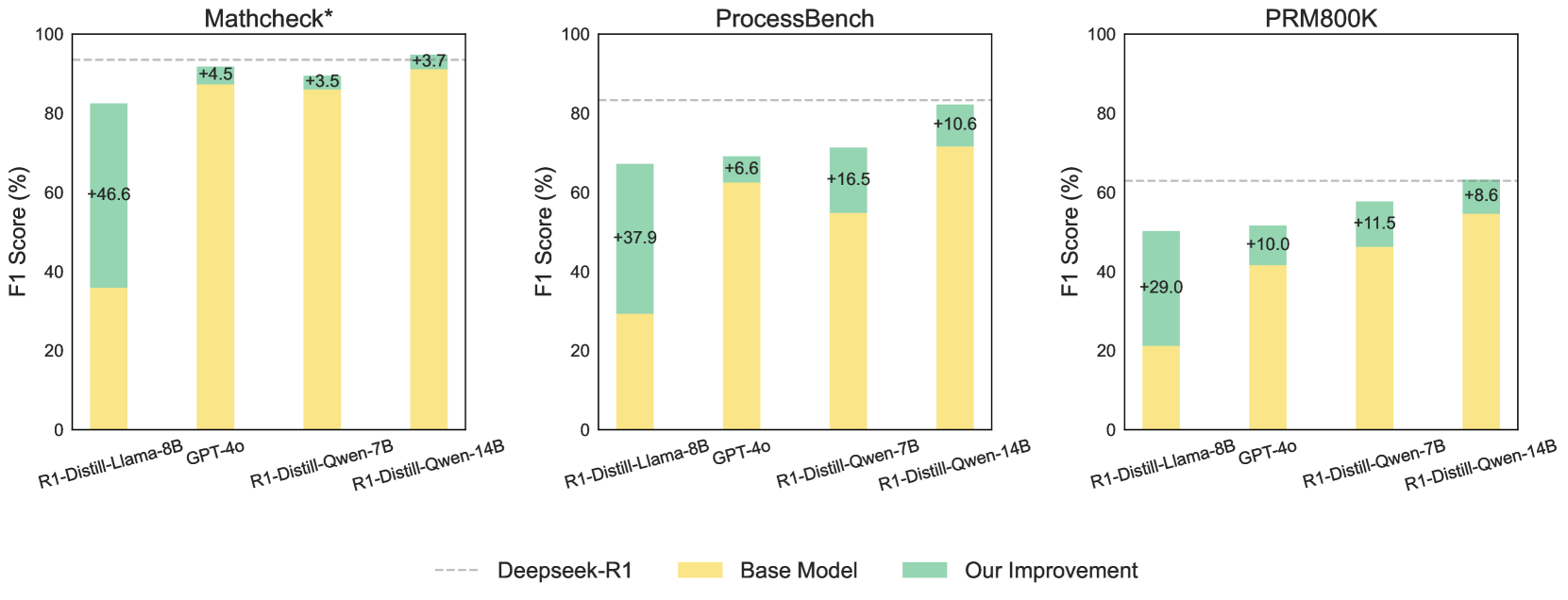
🔼 This figure displays the performance improvements achieved by incorporating the Temporal Consistency method across various large language models (LLMs) on three distinct process error identification benchmarks: Mathcheck*, ProcessBench, and PRM800K. Each bar represents a specific LLM, showcasing the increase in performance (F1 score) gained after integrating the Temporal Consistency method. The baselines shown are for comparison, to illustrate the improvements gained with the new method. Notably, even smaller, distilled LLMs, such as DeepSeek R1 distilled models, demonstrate enhanced performance that surpasses that of larger models and even GPT-40 on certain benchmarks when using the Temporal Consistency method. The improvements are quantified in percentage points for each benchmark.
read the caption
Figure 1: Performance improvements for various models on process error identification benchmarks.
| Model | Method | Mathcheck∗ | ProcessBench | PRM800K |
| GPT-4o mini | Greedy Decoding | 78.8 | 52.9 | 34.0 |
| Majority Voting | 80.4 | 54.2 | 37.9 | |
| Multi-Model Debate | 79.9 | 54.6 | 38.0 | |
| Temporal Consistency (Ours) | 84.8 | 58.2 | 39.0 | |
| GPT-4o | Greedy Decoding | 87.3 | 62.5 | 41.6 |
| Majority Voting | 89.0 | 65.9 | 42.6 | |
| Multi-Model Debate | 90.8 | 66.8 | 50.7 | |
| Temporal Consistency (Ours) | 91.8 | 69.1 | 51.6 | |
| Llama 3.1 8B Instruct | Greedy Decoding | 13.3 | 6.4 | 2.4 |
| Majority Voting | 5.9 | 5.1 | 6.8 | |
| Multi-Model Debate | 6.8 | 5.6 | 2.6 | |
| Temporal Consistency (Ours) | 60.2 | 35.5 | 22.1 | |
| Mistral 7B Instruct v0.3 | Greedy Decoding | 26.4 | 20.3 | 13.0 |
| Majority Voting | 26.3 | 17.6 | 12.1 | |
| Multi-Model Debate | 26.2 | 17.7 | 12.1 | |
| Temporal Consistency (Ours) | 37.4 | 22.5 | 13.3 |
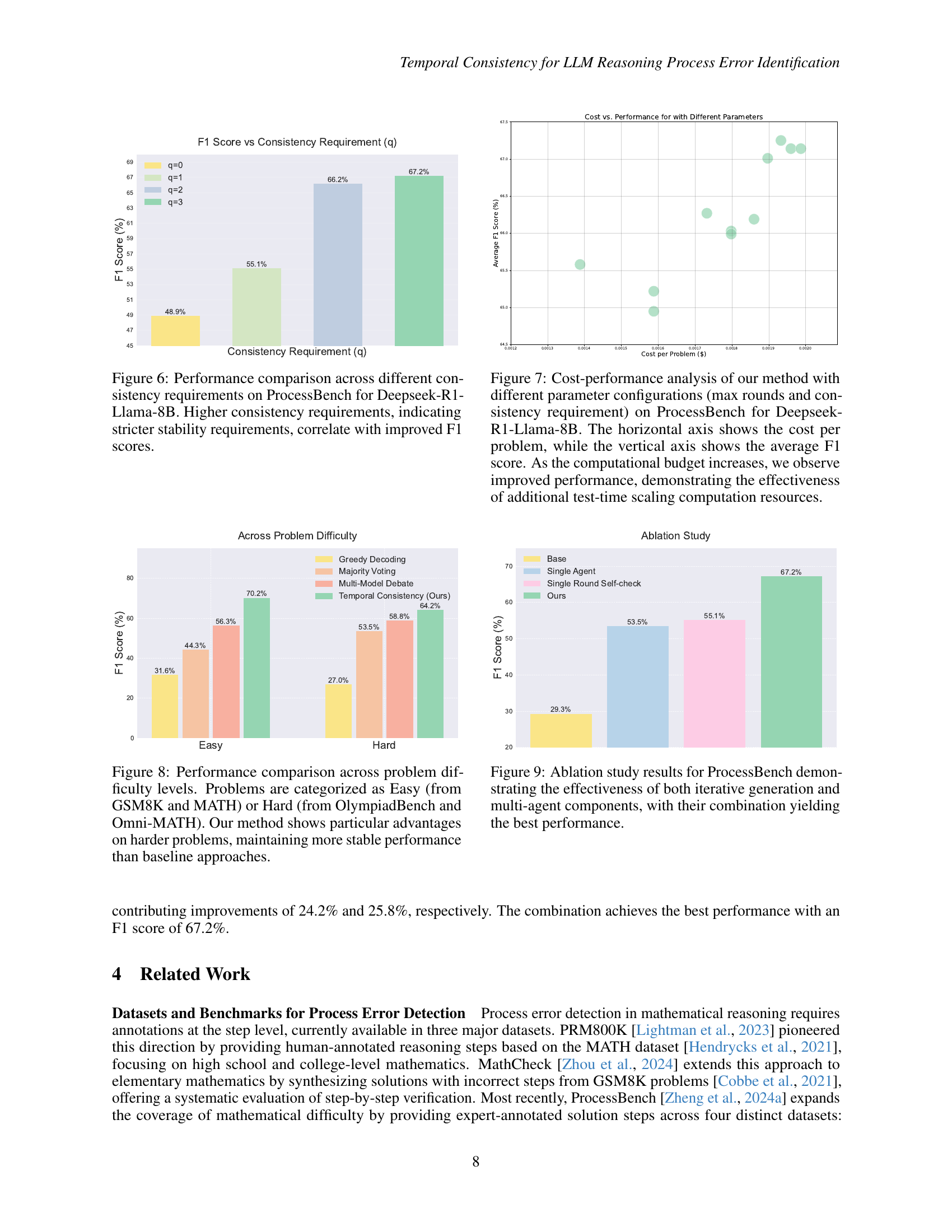
🔼 This table presents a comparison of the F1 scores achieved by different LLMs on three mathematical reasoning benchmarks (Mathcheck*, ProcessBench, and PRM800K) using four different methods: greedy decoding, majority voting, multi-model debate, and the proposed temporal consistency method. The results show the F1 score for each model and method combination. The highest F1 score for each model is highlighted in bold. The table demonstrates that the temporal consistency method consistently outperforms the baseline methods across all models and benchmarks.
read the caption
Table 1: Performance comparison across different models. Numbers represent F1 score (%). The best performance for each model is highlighted in bold. Our method consistently outperforms baselines across all models and benchmarks.
In-depth insights#
Temp. Consistency#
Temporal Consistency seems to be a core concept, likely referring to maintaining consistency in reasoning or decision-making over time. This could involve iteratively refining judgments based on previous assessments, ensuring that conclusions drawn at different points align. This is particularly useful in tasks where perfect information is unavailable, and iterative refinement leads to higher accuracy. A system exhibiting strong temporal consistency would resist drastic changes in output unless warranted by significant new evidence, making it more robust and reliable. The use of temporal consistency could be seen as a way to improve the stability and predictability of LLMs in tasks such as error identification, where maintaining a consistent assessment of errors across multiple rounds of evaluation leads to better accuracy.
Iterative Verify#
An “Iterative Verify” process in an LLM reasoning paper suggests a method where the model repeatedly checks and refines its own reasoning steps. This iterative process could involve the LLM re-evaluating intermediate conclusions or assumptions made during the problem-solving process. The key benefit is the potential to catch and correct errors that might have been missed in a single-pass approach, leading to more robust and accurate results. Furthermore, such a process could improve the model’s calibration, giving it a better sense of when it is confident in its answer. This technique could be resource-intensive but may yield higher quality outputs where accuracy is essential. A core idea could be the use of different prompting strategies to trigger diverse perspectives, or sampling different solution paths, and checking consistency across iterations.
R1 Distill Boost#
While “R1 Distill Boost” isn’t directly present, the paper extensively discusses improvements using distilled versions of DeepSeek R1. This suggests a focus on enhancing smaller models to achieve performance comparable to, or even exceeding, larger models like GPT-40. Key is distilling knowledge from DeepSeek R1 into models like Qwen-7B and Llama-8B, highlighting efficiency and accessibility. The success hinges on techniques that effectively transfer reasoning capabilities, allowing resource-constrained environments to benefit from advanced AI. The distilled models, when coupled with the proposed Temporal Consistency method, demonstrate a significant performance jump, suggesting the distillation process, combined with iterative refinement, is highly effective in improving reasoning accuracy and error identification. This boosts practicality and reduces computational demands.
Test-time Scale#
Test-time scaling is a crucial concept for enhancing language model performance. The core idea revolves around leveraging more computational resources during inference to improve accuracy and reliability. This contrasts with scaling up model parameters, which increases model size and training costs. Iterative refinement with feedback is used to guide output. More sophisticated techniques like search-based methods are being explored. Hybrid frameworks seamlessly integrate tree-based search with sequential approaches. Studies focus on optimizing the test-time scaling across various policy models. This allows models to incorporate feedback and refine results.
Limited Tasks#
While the paper might demonstrate consistent improvements across various settings, it’s crucial to acknowledge that its evaluations are confined to mathematical tasks. The method’s efficacy in other reasoning domains remains uncertain. This specialization could limit the generalizability of the findings. The observed improvements might not directly translate to tasks requiring different cognitive skills or knowledge domains. Future research should explore the method’s applicability across a broader spectrum of reasoning tasks to ascertain its versatility and robustness. The method’s performance is strictly tied to the nature of the mathematical reasoning involved, thus it should be tested in varied tasks.
More visual insights#
More on figures

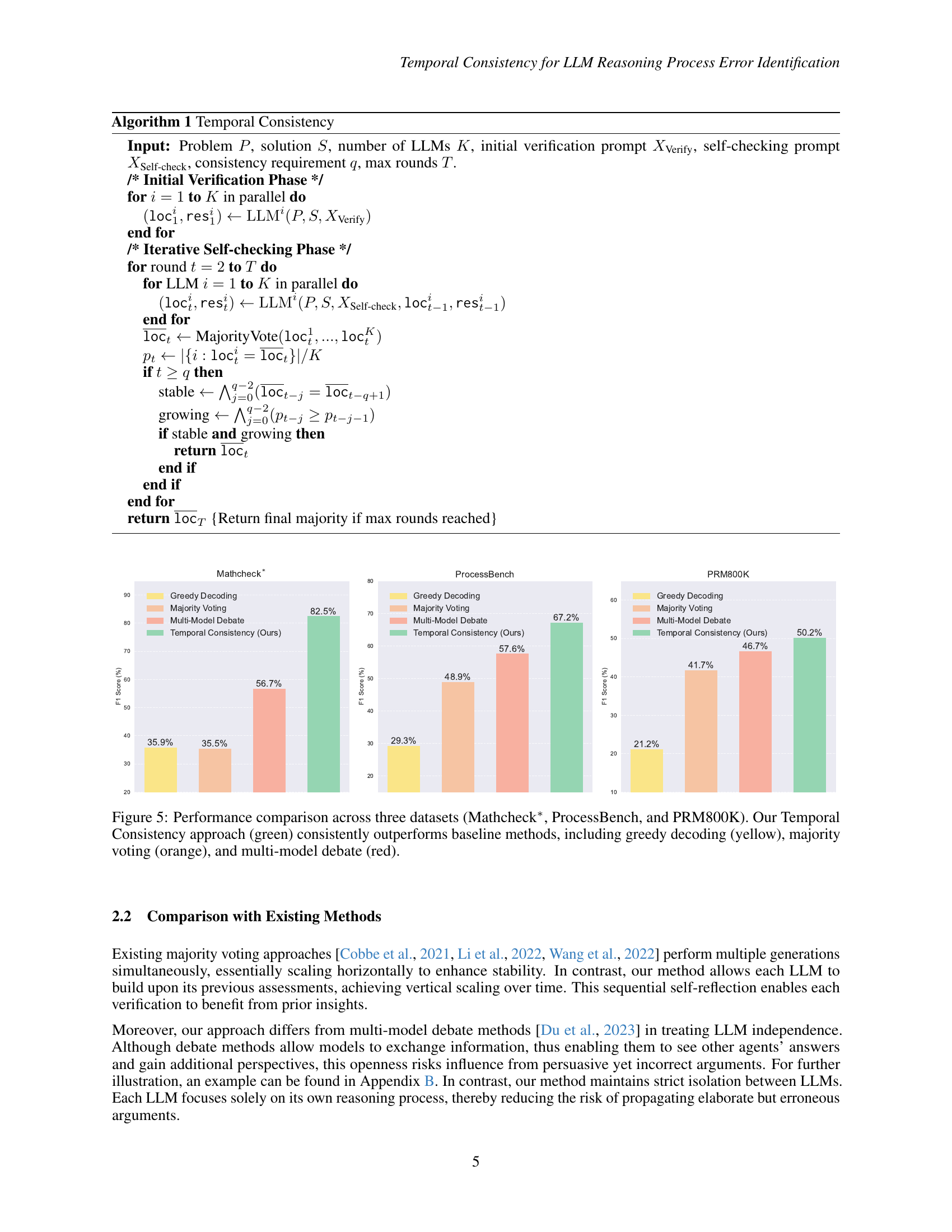
🔼 The figure illustrates the Temporal Consistency approach. It starts with an initial verification phase where multiple LLMs independently assess a problem’s solution. Then, an iterative self-checking phase begins. Each LLM reviews its own initial assessment, potentially correcting errors based on its previous judgment. This process continues until a convergence criterion, defined in Section 2 of the paper, is met, resulting in a consistent final output.
read the caption
Figure 2: Overview of our Temporal Consistency approach, where each LLM iteratively examines its own verification results until reaching a stable result (stopping criteria defined in Section 2). The self-checking mechanism allows LLMs to refine their judgments based on previous verifications, potentially correcting initial misidentification.

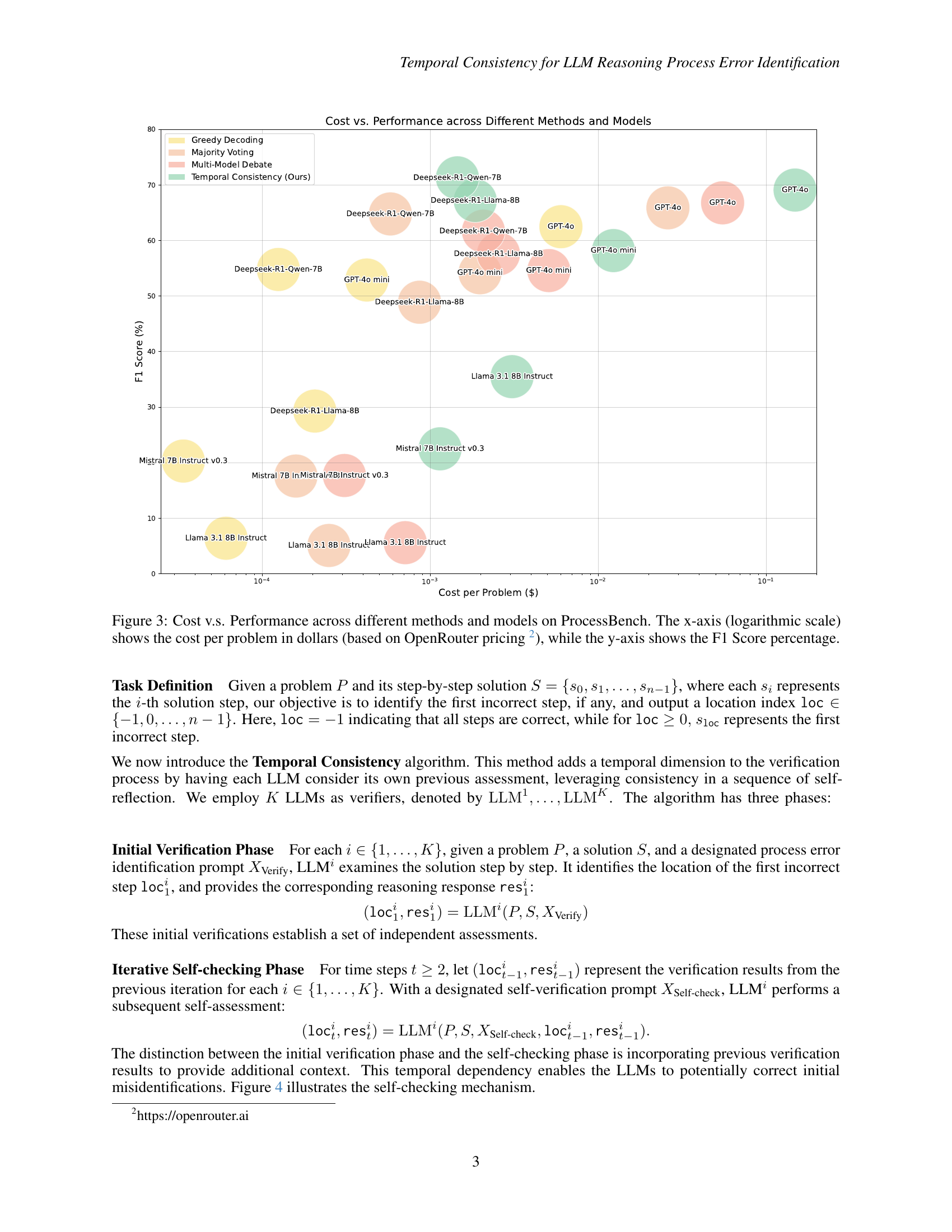
🔼 This figure illustrates the trade-off between cost and performance for various Large Language Models (LLMs) and methods on the ProcessBench benchmark. The x-axis represents the cost per problem in US dollars, calculated using the OpenRouter pricing model. The y-axis shows the F1 score, a metric that assesses the accuracy of the models in identifying process errors. The figure compares four different methods: Greedy Decoding, Majority Voting, Multi-Model Debate, and the proposed Temporal Consistency method. Each method’s performance is evaluated across several different LLMs, showcasing how the cost and performance vary depending on the model and method used.
read the caption
Figure 3: Cost v.s. Performance across different methods and models on ProcessBench. The x-axis (logarithmic scale) shows the cost per problem in dollars (based on OpenRouter pricing 333https://openrouter.ai), while the y-axis shows the F1 Score percentage.
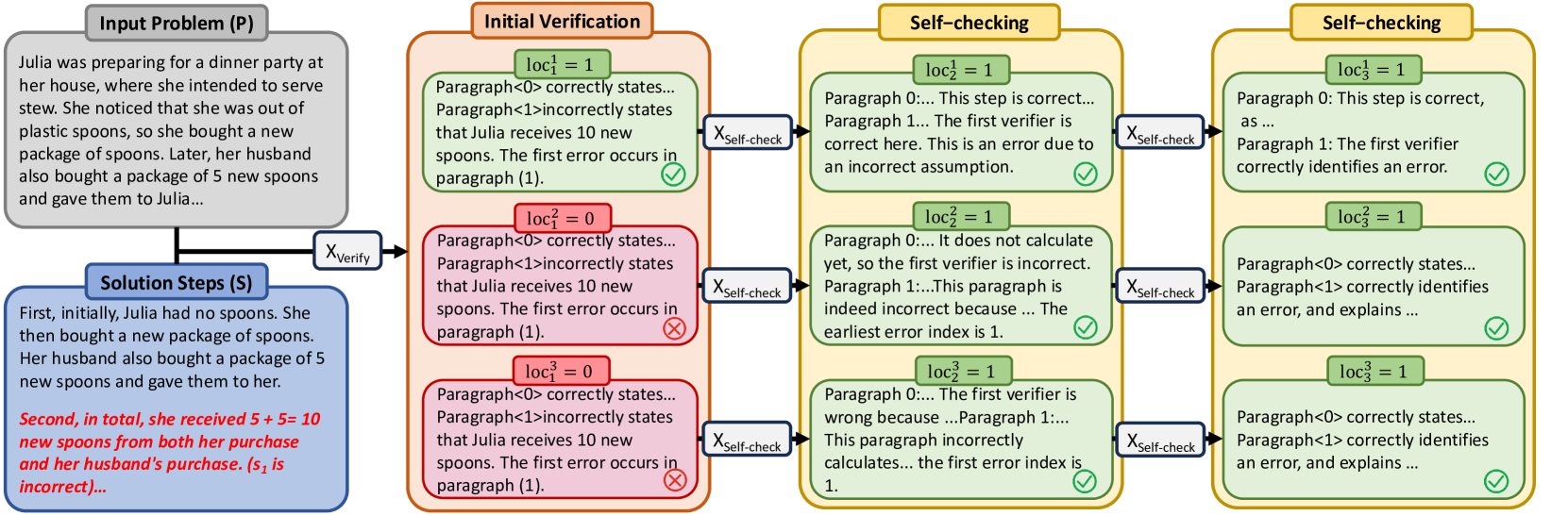
🔼 Figure 4 illustrates the iterative process of the Temporal Consistency method. The example shows a problem where the first error occurs in step 1. Initially, two out of three LLMs incorrectly identify the location of the first error. However, through the iterative self-checking phase, where LLMs review their own initial assessments, the model’s internal consistency improves. Eventually, after multiple rounds of self-checking, all three LLMs converge on the correct identification of the error in step 1.
read the caption
Figure 4: Example of the self-checking process: The first error occurred in step 1. Initially, two LLMs incorrectly identified the first incorrect step, while one correctly located the first incorrect step. After self-checking, all LLMs achieve the correct identification.

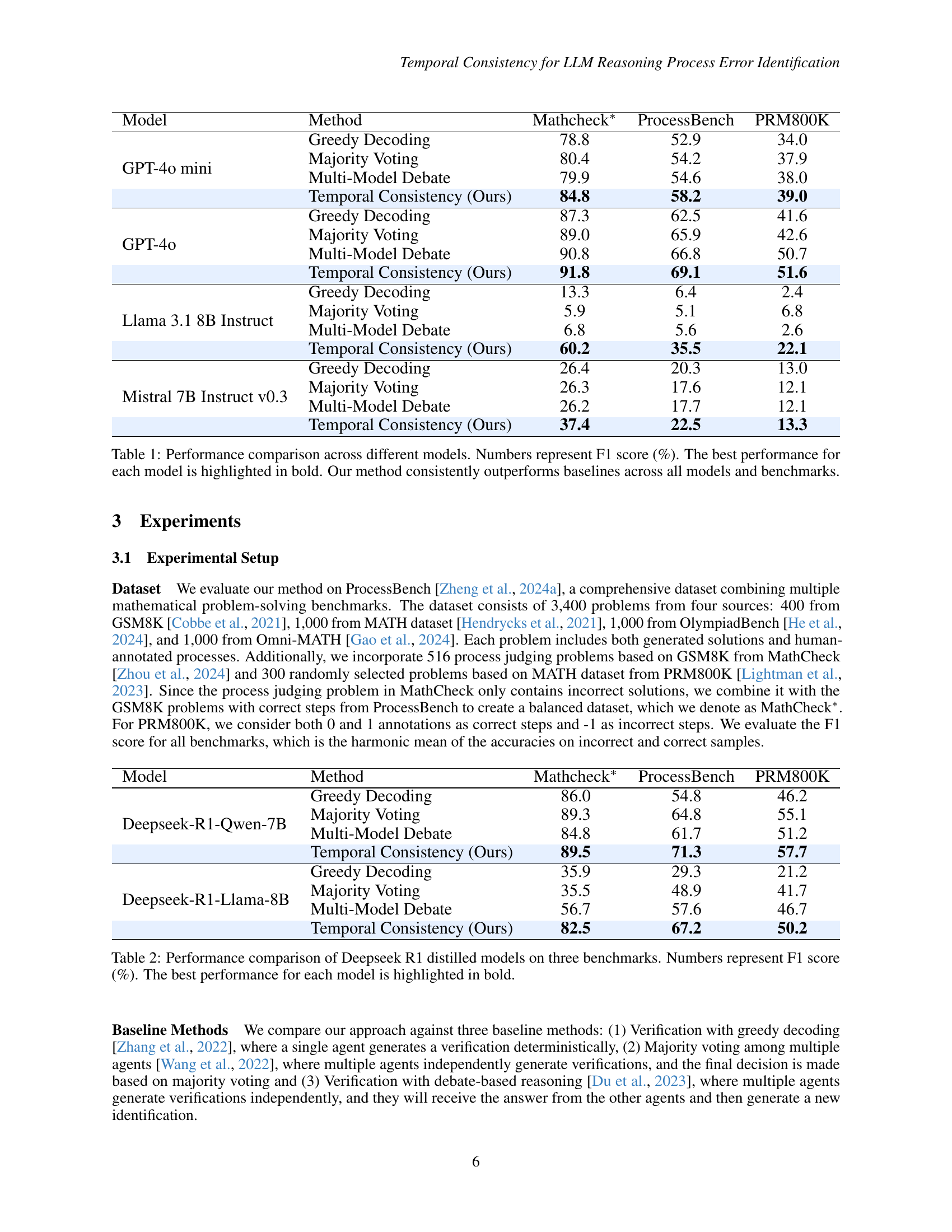
🔼 Figure 5 illustrates a comparison of the performance of four different methods for identifying errors in the reasoning process of large language models (LLMs) across three benchmark datasets: Mathcheck*, ProcessBench, and PRM800K. The methods compared include greedy decoding, majority voting, multi-model debate, and the authors’ proposed Temporal Consistency approach. Each bar represents the F1-score achieved by each method on each dataset. The results clearly show that the Temporal Consistency method outperforms all other baseline methods across all three datasets, indicating its effectiveness in improving the accuracy of LLM reasoning process error identification.
read the caption
Figure 5: Performance comparison across three datasets (Mathcheck∗, ProcessBench, and PRM800K). Our Temporal Consistency approach (green) consistently outperforms baseline methods, including greedy decoding (yellow), majority voting (orange), and multi-model debate (red).

🔼 This figure illustrates the impact of the consistency requirement parameter in the Temporal Consistency algorithm on the ProcessBench benchmark using the Deepseek-R1-Llama-8B model. The x-axis represents the value of the consistency requirement (q). The y-axis shows the F1 score, a metric that evaluates the accuracy of the model in identifying process errors. As the consistency requirement (q) increases, indicating stricter stability requirements, the F1 score improves, demonstrating that the algorithm’s performance is enhanced by imposing stronger consistency constraints on the iterative self-checking process.
read the caption
Figure 6: Performance comparison across different consistency requirements on ProcessBench for Deepseek-R1-Llama-8B. Higher consistency requirements, indicating stricter stability requirements, correlate with improved F1 scores.

🔼 This figure analyzes the cost-effectiveness of the Temporal Consistency method by varying the number of iterations (max rounds) and the consistency threshold (consistency requirement). The x-axis represents the computational cost per problem (likely reflecting the number of LLM calls), and the y-axis shows the average F1 score achieved on the ProcessBench dataset using the Deepseek-R1-Llama-8B model. The results indicate that increasing computational budget, by allowing more iterations and stricter consistency requirements, leads to improved performance in identifying process errors.
read the caption
Figure 7: Cost-performance analysis of our method with different parameter configurations (max rounds and consistency requirement) on ProcessBench for Deepseek-R1-Llama-8B. The horizontal axis shows the cost per problem, while the vertical axis shows the average F1 score. As the computational budget increases, we observe improved performance, demonstrating the effectiveness of additional test-time scaling computation resources.

🔼 Figure 8 illustrates the performance of different methods (Greedy Decoding, Majority Voting, Multi-Model Debate, and Temporal Consistency) on solving mathematical problems categorized by difficulty level (Easy and Hard). Easy problems are sourced from GSM8K and MATH datasets, while Hard problems come from OlympiadBench and Omni-MATH datasets. The figure highlights that the Temporal Consistency method exhibits superior performance, especially on more challenging (Hard) problems, showcasing more consistent results compared to the baseline methods.
read the caption
Figure 8: Performance comparison across problem difficulty levels. Problems are categorized as Easy (from GSM8K and MATH) or Hard (from OlympiadBench and Omni-MATH). Our method shows particular advantages on harder problems, maintaining more stable performance than baseline approaches.

🔼 Figure 9 shows the results of an ablation study conducted on the ProcessBench dataset to evaluate the individual and combined contributions of iterative generation and multi-agent components to the overall performance of the Temporal Consistency method. The figure demonstrates that both iterative generation and the multi-agent approach significantly improve performance compared to a baseline greedy decoding method. However, the combination of both methods yields the best performance, highlighting the synergistic effect of these two components in enhancing the accuracy of process error identification.
read the caption
Figure 9: Ablation study results for ProcessBench demonstrating the effectiveness of both iterative generation and multi-agent components, with their combination yielding the best performance.
More on tables
| Model | Method | Mathcheck∗ | ProcessBench | PRM800K |
| Deepseek-R1-Qwen-7B | Greedy Decoding | 86.0 | 54.8 | 46.2 |
| Majority Voting | 89.3 | 64.8 | 55.1 | |
| Multi-Model Debate | 84.8 | 61.7 | 51.2 | |
| Temporal Consistency (Ours) | 89.5 | 71.3 | 57.7 | |
| Deepseek-R1-Llama-8B | Greedy Decoding | 35.9 | 29.3 | 21.2 |
| Majority Voting | 35.5 | 48.9 | 41.7 | |
| Multi-Model Debate | 56.7 | 57.6 | 46.7 | |
| Temporal Consistency (Ours) | 82.5 | 67.2 | 50.2 |
🔼 This table presents a performance comparison of DeepSeek R1 distilled models (Deepseek-R1-Distill-Qwen-7B and Deepseek-R1-Llama-8B) on three mathematical reasoning benchmarks: Mathcheck*, ProcessBench, and PRM800K. For each model and benchmark, the table shows the F1 score achieved using four different methods: Greedy Decoding, Majority Voting, Multi-Model Debate, and Temporal Consistency (the authors’ proposed method). The F1 score is a measure of the model’s accuracy in identifying process errors within the problem solutions. The best-performing method for each model on each benchmark is highlighted in bold, illustrating the effectiveness of the Temporal Consistency method in improving the accuracy of distilled models.
read the caption
Table 2: Performance comparison of Deepseek R1 distilled models on three benchmarks. Numbers represent F1 score (%). The best performance for each model is highlighted in bold.
| Model Method | Err | Cor | F1 |
| GPT-4o mini Greedy Decoding | 75.0 | 82.9 | 78.8 |
| Majority Voting | 76.2 | 85.0 | 80.4 |
| Multi-Model Debate | 79.5 | 80.3 | 79.9 |
| Temporal Consistency (Ours) | 84.7 | 85.0 | 84.8 |
| GPT-4o Greedy Decoding | 84.5 | 90.2 | 87.3 |
| Majority Voting | 85.1 | 93.3 | 89.0 |
| Multi-Model Debate | 88.4 | 93.3 | 90.8 |
| Temporal Consistency (Ours) | 89.0 | 94.8 | 91.8 |
| Llama 3.1 8B Instruct Greedy Decoding | 44.6 | 7.8 | 13.3 |
| Majority Voting | 64.7 | 3.1 | 5.9 |
| Multi-Model Debate | 62.2 | 3.6 | 6.8 |
| Temporal Consistency (Ours) | 55.8 | 65.3 | 60.2 |
| Mistral 7B Instruct v0.3 Greedy Decoding | 24.6 | 28.5 | 26.4 |
| Majority Voting | 15.9 | 76.2 | 26.3 |
| Multi-Model Debate | 15.7 | 79.3 | 26.2 |
| Temporal Consistency (Ours) | 34.1 | 41.5 | 37.4 |
| Deepseek-R1-Llama-8B Greedy Decoding | 67.6 | 24.4 | 35.9 |
| Majority Voting | 79.8 | 22.8 | 35.5 |
| Multi-Model Debate | 75.0 | 45.6 | 56.7 |
| Temporal Consistency (Ours) | 81.2 | 83.9 | 82.5 |
| Deepseek-R1-Qwen-7B Greedy Decoding | 77.9 | 95.9 | 86.0 |
| Majority Voting | 81.6 | 99.0 | 89.3 |
| Multi-Model Debate | 77.3 | 93.8 | 84.8 |
| Temporal Consistency (Ours) | 82.0 | 98.4 | 89.5 |
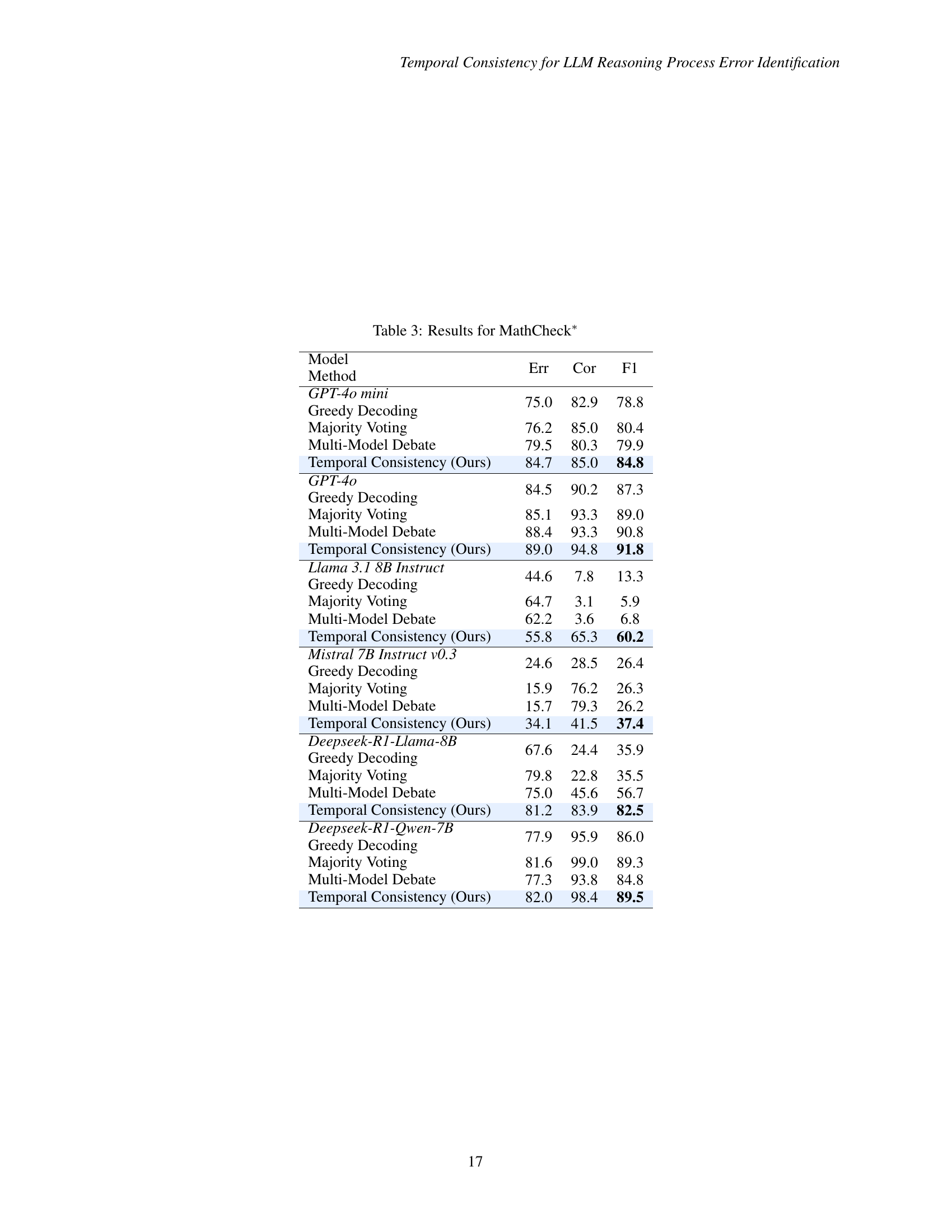
🔼 This table presents the performance of various LLMs on the MathCheck* benchmark, specifically focusing on process error identification. It compares four different LLMs (GPT-40 mini, GPT-40, Llama 3.1 8B Instruct, and Mistral 7B Instruct v0.3) along with two distilled models (Deepseek-R1-Llama-8B and Deepseek-R1-Qwen-7B). For each model, it shows the results of four methods: greedy decoding, majority voting, multi-model debate, and the proposed temporal consistency method. The metrics used for evaluation are error rate, correct rate, and F1 score. The table highlights the consistent superior performance of the temporal consistency method across all models and metrics.
read the caption
Table 3: Results for MathCheck∗
| Model Method | Err | Cor | F1 |
| GPT-4o mini Greedy Decoding | 27.8 | 43.8 | 34.0 |
| Majority Voting | 31.3 | 47.9 | 37.9 |
| Multi-Model Debate | 34.4 | 42.5 | 38.0 |
| Temporal Consistency (Ours) | 34.4 | 45.2 | 39.0 |
| GPT-4o Greedy Decoding | 30.4 | 65.8 | 41.6 |
| Majority Voting | 30.4 | 71.2 | 42.6 |
| Multi-Model Debate | 41.9 | 64.4 | 50.7 |
| Temporal Consistency (Ours) | 39.2 | 75.3 | 51.6 |
| Llama 3.1 8B Instruct Greedy Decoding | 10.1 | 1.4 | 2.4 |
| Majority Voting | 18.9 | 4.1 | 6.8 |
| Multi-Model Debate | 23.3 | 1.4 | 2.6 |
| Temporal Consistency (Ours) | 15.0 | 42.5 | 22.1 |
| Mistral 7B Instruct v0.3 Greedy Decoding | 11.5 | 15.1 | 13.0 |
| Majority Voting | 6.6 | 71.2 | 12.1 |
| Multi-Model Debate | 6.6 | 71.2 | 12.1 |
| Temporal Consistency (Ours) | 10.6 | 17.8 | 13.3 |
| Deepseek-R1-Llama-8B Greedy Decoding | 30.0 | 16.4 | 21.2 |
| Majority Voting | 41.0 | 42.5 | 41.7 |
| Multi-Model Debate | 42.3 | 52.1 | 46.7 |
| Temporal Consistency (Ours) | 39.2 | 69.9 | 50.2 |
| Deepseek-R1-Qwen-7B Greedy Decoding | 33.9 | 72.6 | 46.2 |
| Majority Voting | 41.9 | 80.8 | 55.1 |
| Multi-Model Debate | 38.8 | 75.3 | 51.2 |
| Temporal Consistency (Ours) | 44.5 | 82.2 | 57.7 |
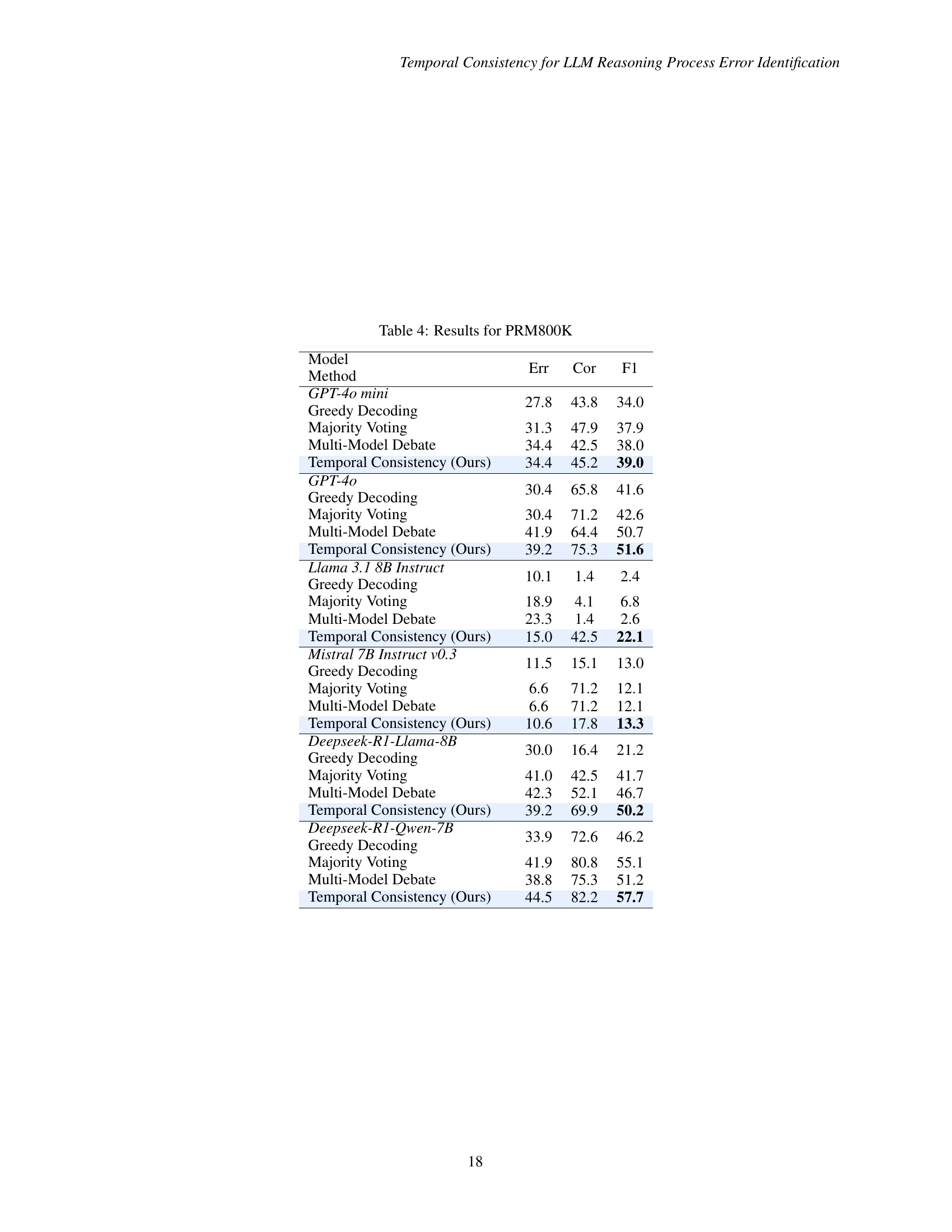
🔼 This table presents the performance of different methods (Greedy Decoding, Majority Voting, Multi-Model Debate, and Temporal Consistency) on the PRM800K benchmark. It shows the error rate, correct rate, and F1 score for each method across various LLM models (GPT-40 mini, GPT-40, Llama 3.1 8B Instruct, Mistral 7B Instruct v0.3, Deepseek-R1-Llama-8B, and Deepseek-R1-Qwen-7B). The results highlight the effectiveness of the Temporal Consistency method in improving the accuracy of process error identification.
read the caption
Table 4: Results for PRM800K
| ProcessBench | ||||||||||||
| Model Method | GSM8K | MATH | OlympiadBench | Omni-MATH | ||||||||
| Err | Cor | F1 | Err | Cor | F1 | Err | Cor | F1 | Err | Cor | F1 | |
| GPT-4o mini Greedy Decoding | 54.1 | 82.9 | 65.5 | 47.0 | 69.2 | 56.0 | 39.0 | 55.2 | 45.7 | 35.7 | 58.1 | 44.2 |
| Majority Voting | 56.0 | 85.0 | 67.5 | 47.8 | 71.6 | 57.3 | 38.9 | 60.5 | 47.3 | 36.1 | 58.1 | 44.5 |
| Multi-Model Debate | 63.8 | 80.3 | 71.1 | 52.9 | 64.4 | 58.1 | 42.1 | 49.9 | 45.6 | 40.3 | 47.7 | 43.7 |
| Temporal Consistency (Ours) | 63.3 | 85.0 | 72.5 | 51.3 | 74.1 | 60.7 | 43.1 | 60.8 | 50.4 | 41.2 | 61.0 | 49.2 |
| GPT-4o Greedy Decoding | 70.0 | 90.2 | 78.8 | 53.4 | 77.1 | 63.1 | 44.8 | 67.0 | 53.7 | 46.4 | 65.1 | 54.2 |
| Majority Voting | 73.4 | 93.3 | 82.2 | 53.9 | 82.5 | 65.2 | 48.3 | 72.8 | 58.0 | 49.2 | 71.4 | 58.3 |
| Multi-Model Debate | 77.8 | 93.3 | 84.8 | 61.4 | 77.0 | 68.4 | 53.7 | 59.5 | 56.4 | 56.1 | 58.9 | 57.5 |
| Temporal Consistency (Ours) | 74.9 | 94.8 | 83.7 | 58.1 | 90.1 | 70.6 | 45.8 | 86.7 | 60.0 | 48.7 | 86.3 | 62.2 |
| Llama 3.1 8B Instruct Greedy Decoding | 23.7 | 7.8 | 11.7 | 16.5 | 2.5 | 4.3 | 8.3 | 3.2 | 4.7 | 7.8 | 3.7 | 5.0 |
| Majority Voting | 41.1 | 3.1 | 5.8 | 30.6 | 1.7 | 3.3 | 19.8 | 4.1 | 6.8 | 25.4 | 2.5 | 4.5 |
| Multi-Model Debate | 45.9 | 3.6 | 6.7 | 37.9 | 3.7 | 6.7 | 30.6 | 2.9 | 5.4 | 32.0 | 2.5 | 4.6 |
| Temporal Consistency (Ours) | 34.8 | 65.3 | 45.4 | 28.8 | 51.5 | 36.9 | 23.8 | 37.5 | 29.1 | 24.6 | 40.7 | 30.7 |
| Mistral 7B Instruct v0.3 Greedy Decoding | 27.1 | 28.5 | 27.8 | 23.7 | 20.9 | 22.2 | 14.8 | 14.7 | 14.8 | 16.3 | 16.2 | 16.3 |
| Majority Voting | 12.6 | 76.2 | 21.6 | 11.8 | 69.7 | 20.2 | 7.6 | 65.8 | 13.6 | 8.4 | 67.2 | 15.0 |
| Multi-Model Debate | 12.6 | 79.3 | 21.7 | 12.0 | 70.2 | 20.4 | 7.3 | 67.0 | 13.1 | 8.7 | 66.0 | 15.4 |
| Temporal Consistency (Ours) | 20.8 | 41.5 | 27.7 | 19.4 | 25.9 | 22.1 | 18.0 | 19.8 | 18.8 | 16.2 | 31.5 | 21.4 |
| Deepseek-R1-Llama-8B Greedy Decoding | 44.9 | 24.4 | 31.6 | 45.5 | 24.1 | 31.5 | 35.1 | 24.8 | 29.0 | 31.2 | 20.7 | 24.9 |
| Majority Voting | 49.3 | 22.8 | 31.2 | 67.5 | 50.0 | 57.4 | 57.3 | 58.7 | 58.0 | 51.8 | 46.5 | 49.0 |
| Multi-Model Debate | 51.7 | 45.6 | 48.5 | 64.5 | 63.8 | 64.1 | 56.1 | 71.1 | 62.7 | 49.9 | 61.0 | 54.9 |
| Temporal Consistency (Ours) | 56.5 | 83.9 | 67.6 | 67.0 | 79.6 | 72.7 | 57.0 | 78.5 | 66.1 | 53.1 | 75.1 | 62.2 |
| Deepseek-R1-Qwen-7B Greedy Decoding | 52.2 | 95.9 | 67.6 | 50.5 | 80.0 | 61.9 | 39.0 | 64.6 | 48.7 | 29.6 | 66.0 | 40.9 |
| Majority Voting | 57.5 | 99.0 | 72.7 | 64.3 | 88.4 | 74.5 | 48.1 | 81.7 | 60.6 | 39.0 | 75.5 | 51.4 |
| Multi-Model Debate | 58.0 | 93.8 | 71.7 | 59.8 | 84.7 | 70.1 | 45.8 | 71.1 | 55.7 | 37.7 | 71.4 | 49.3 |
| Temporal Consistency (Ours) | 62.8 | 98.4 | 76.7 | 69.5 | 94.3 | 80.1 | 54.5 | 90.6 | 68.0 | 46.1 | 86.7 | 60.2 |
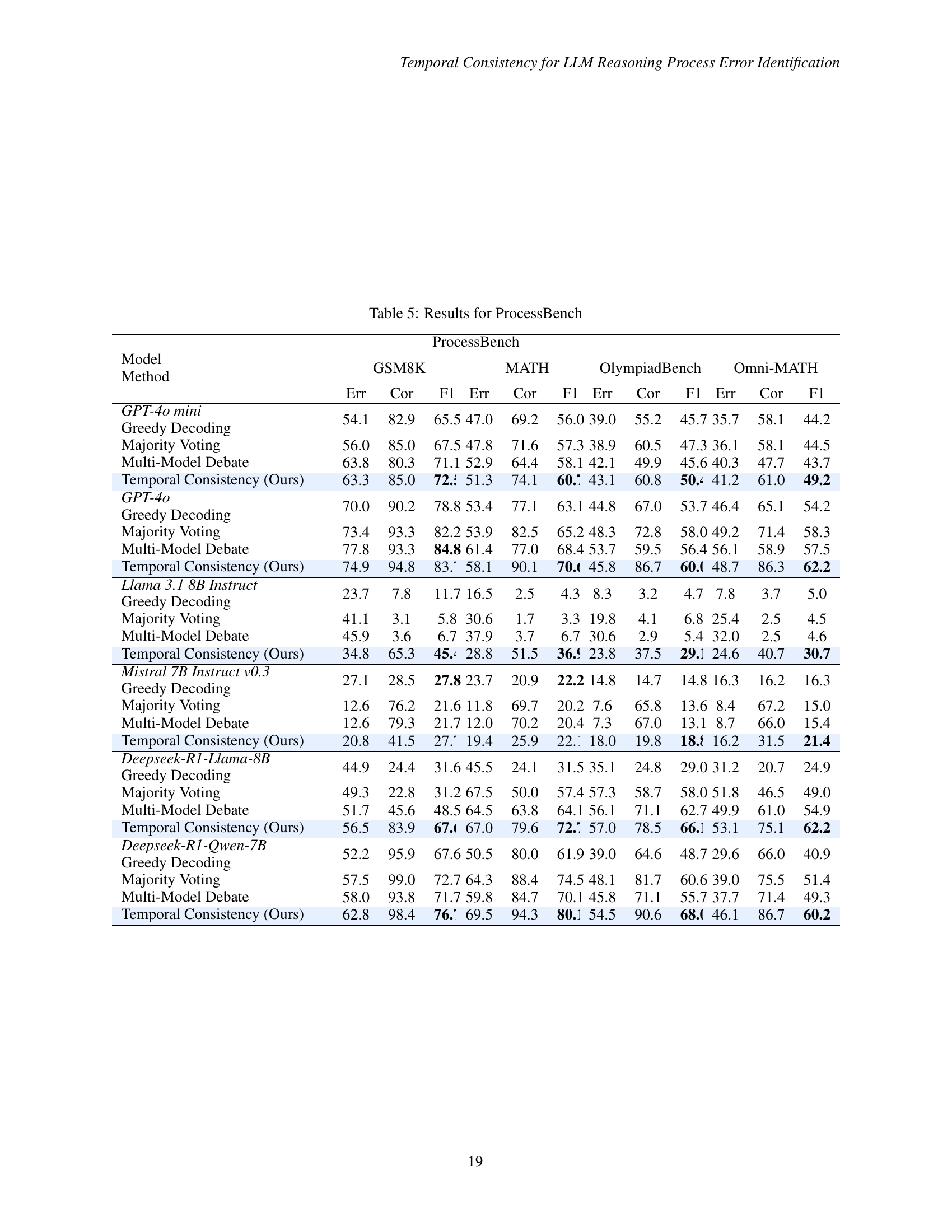
🔼 This table presents a comprehensive breakdown of the performance achieved by various LLMs on the ProcessBench benchmark. It shows the results for different models (GPT-40 mini, GPT-40, Llama 3.1 8B Instruct, Mistral 7B Instruct v0.3, Deepseek-R1-Llama-8B, and Deepseek-R1-Qwen-7B) across four subsets of the benchmark: GSM8K, MATH, OlympiadBench, and Omni-MATH. For each model and subset, the table reports the error rate, correct rate, and F1 score obtained using different methods: Greedy Decoding, Majority Voting, Multi-Model Debate, and Temporal Consistency (the proposed method). This detailed analysis allows for a comprehensive comparison of the different methods and models across various aspects of mathematical reasoning.
read the caption
Table 5: Results for ProcessBench
Full paper#