TL;DR#
Large Language Models show promise in mathematical reasoning, but current data augmentation is limited to instance-level modifications, failing to capture relational structures. To address this, the paper introduces MathFusion. It draws inspiration from human learning, where math proficiency grows via interconnected concepts, enhancing reasoning through cross-problem instruction synthesis. The new framework uses 3 fusion strategies: sequential, parallel, and conditional fusion.
The paper generates MathFusionQA, then fine-tunes models(DeepSeekMath-7B, Mistral-7B, Llama3-8B). MathFusion enhances mathematical reasoning while maintaining efficiency, boosting performance by 18.0 points in accuracy across benchmarks with only 45K additional instructions. MathFusion enables LLMs to capture underlying relational structures, improving complex, multi-step problem-solving. The models achieve better performance on diverse benchmarks.
Key Takeaways#
Why does it matter?#
This paper introduces MathFusion, a novel method for improving mathematical reasoning in LLMs, addressing a critical need for more effective data augmentation techniques. It offers a new paradigm for enhancing LLMs’ problem-solving capabilities, potentially impacting various fields relying on advanced AI reasoning. It also opens avenues for exploring relational learning in other complex domains.
Visual Insights#

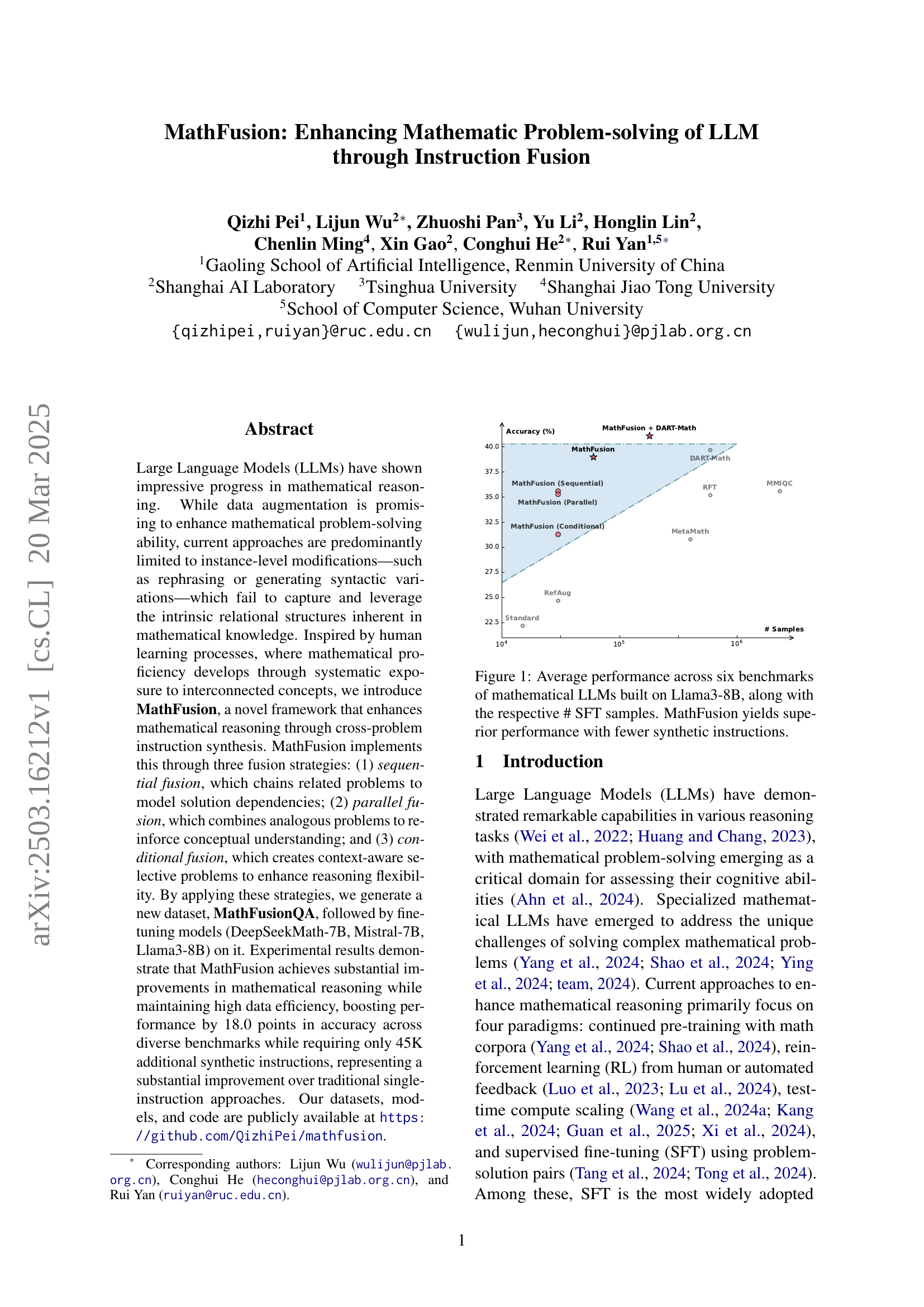
🔼 The figure displays the average accuracy of several large language models (LLMs) fine-tuned for mathematical problem-solving, all based on the Llama3-8B architecture. Each model was trained using a different method and varying numbers of synthetic instruction samples. The x-axis represents the number of synthetic samples used in supervised fine-tuning (SFT), while the y-axis represents the model’s average accuracy across six standard mathematical reasoning benchmarks. The graph visually demonstrates that the MathFusion approach achieves superior performance compared to other methods, using significantly fewer synthetic instructions.
read the caption
Figure 1: Average performance across six benchmarks of mathematical LLMs built on Llama3-8B, along with the respective # SFT samples. MathFusion yields superior performance with fewer synthetic instructions.
| Dataset | # Samples |
| WizardMath (Luo et al., 2023) | 96K |
| MetaMathQA (Yu et al., 2024) | 395K |
| MMIQC (Liu et al., 2024) | 2294K |
| Orca-Math (Mitra et al., 2024) | 200K |
| Xwin-Math-V1.1 (Li et al., 2024a) | 1440K |
| KPMath-Plus (Huang et al., 2024) | 1576K |
| MathScaleQA (Tang et al., 2024) | 2021K |
| DART-Math-Uniform (Tong et al., 2024) | 591K |
| DART-Math-Hard (Tong et al., 2024) | 585K |
| RefAug (Zhang et al., 2024) | 30K |
| MathFusionQA | 60K |
🔼 This table compares the MathFusionQA dataset with other existing mathematical datasets used for training and evaluating large language models (LLMs). The comparison focuses on the number of samples (problem-solution pairs) in each dataset. The key takeaway is that MathFusionQA is significantly smaller in size than the other datasets, demonstrating its data efficiency.
read the caption
Table 1: Comparison between MathFusionQA and previous mathematical datasets. Our MathFusionQA is generally smaller than others.
In-depth insights#
LLM Math Fusion#
LLM Math Fusion could involve innovative techniques to enhance mathematical reasoning in large language models (LLMs). One approach might center on data augmentation, moving beyond simple rephrasing to fuse diverse problem types. This could capture relational structures inherent in mathematical knowledge. The fusion strategies may vary, e.g., sequencing dependent problems or combining analogous ones. Datasets generated this way, like MathFusionQA, could lead to substantial improvements in mathematical reasoning. The method aims at creating more challenging problems that LLMs can learn from.
Instruction Synth#
Instruction synthesis is vital for enhancing LLMs’ problem-solving. It involves crafting new instructions by strategically combining existing ones. Methods include: sequential fusion (chaining problems), parallel fusion (analogous problems), and conditional fusion (context-aware, selective problems). This approach contrasts with instance-level modifications that only rephrase or vary syntax. Instruction synthesis aims to capture relational structures within the problem space, leading to more robust reasoning. Careful creation and validation are important to make the fused instructions sensible.
Multi-Problem RL#
Multi-Problem RL, while not explicitly present, could allude to an agent excelling across diverse tasks. This highlights the challenge of creating adaptable agents. MathFusion implicitly addresses this by fusing diverse problem types, training models to generalize, and improve OOD performance. It fosters transfer learning between interrelated math concepts, crucial for real-world problem-solving. Future directions might involve curriculum learning, starting with simpler fused problems before escalating complexity. Exploring meta-learning algorithms could further optimize the model’s adaptability to new problem combinations. This aligns with broader efforts to create robust AI agents capable of tackling unforeseen situations.
MathFusionQA Data#
Based on the paper, the MathFusionQA dataset is a novel resource created to enhance mathematical reasoning in LLMs. It is built by applying three fusion strategies—sequential, parallel, and conditional—to existing datasets like GSM8K and MATH. These strategies synthesize new problems by linking related problems, integrating analogous concepts, and generating context-aware selective problems. The construction of MathFusionQA involves identifying suitable problem pairs for fusion, then using strong LLMs to generate corresponding solutions, resulting in high-quality training data. The dataset is designed to improve LLMs’ ability to capture the relational structures inherent in mathematical knowledge, enabling them to tackle complex, multi-step problems more effectively. Its size is generally smaller than many existing mathematical datasets, MathFusionQA stands out due to its targeted approach to instruction synthesis. Experimental results demonstrate its effectiveness in improving mathematical reasoning while maintaining high data efficiency.
Context Matters#
Context fundamentally shapes understanding and problem-solving. In mathematical reasoning, as highlighted in the paper, context is the web of interconnected concepts and relationships, not just isolated facts. This means that effective problem-solving requires understanding how different pieces of information relate to each other within a given scenario. The paper’s approach of instruction fusion directly addresses this by creating new problems that explicitly link different mathematical concepts, mirroring how humans develop expertise through exposure to interconnected ideas. Ignoring context leads to brittle models, unable to generalize beyond the specific examples they were trained on. By actively constructing and training on context-rich examples, LLMs can potentially develop a deeper understanding of mathematical principles and improve their ability to reason effectively in novel situations.
More visual insights#
More on figures

🔼 The figure illustrates the MathFusion framework. It begins with two mathematical problems, PA and PB, selected from an existing dataset. MathFusion then applies three different fusion strategies to these problems to create a new, synthesized problem, PF. These strategies are: 1. Sequential Fusion: Chains problems together to model solution dependencies. 2. Parallel Fusion: Combines analogous problems to reinforce conceptual understanding. 3. Conditional Fusion: Creates context-aware problems to enhance reasoning flexibility. The resulting new problem, PF, incorporates elements and relationships from both PA and PB, reflecting the chosen fusion strategy.
read the caption
Figure 2: The overview of MathFusion. Given two mathematical problems PAsubscript𝑃𝐴P_{A}italic_P start_POSTSUBSCRIPT italic_A end_POSTSUBSCRIPT and PBsubscript𝑃𝐵P_{B}italic_P start_POSTSUBSCRIPT italic_B end_POSTSUBSCRIPT from the original mathematical dataset, MathFusion synthesizes a new mathematical problem PFsubscript𝑃𝐹P_{F}italic_P start_POSTSUBSCRIPT italic_F end_POSTSUBSCRIPT by fusing these two problems through three fusion strategies: sequential fusion, parallel fusion, and conditional fusion.

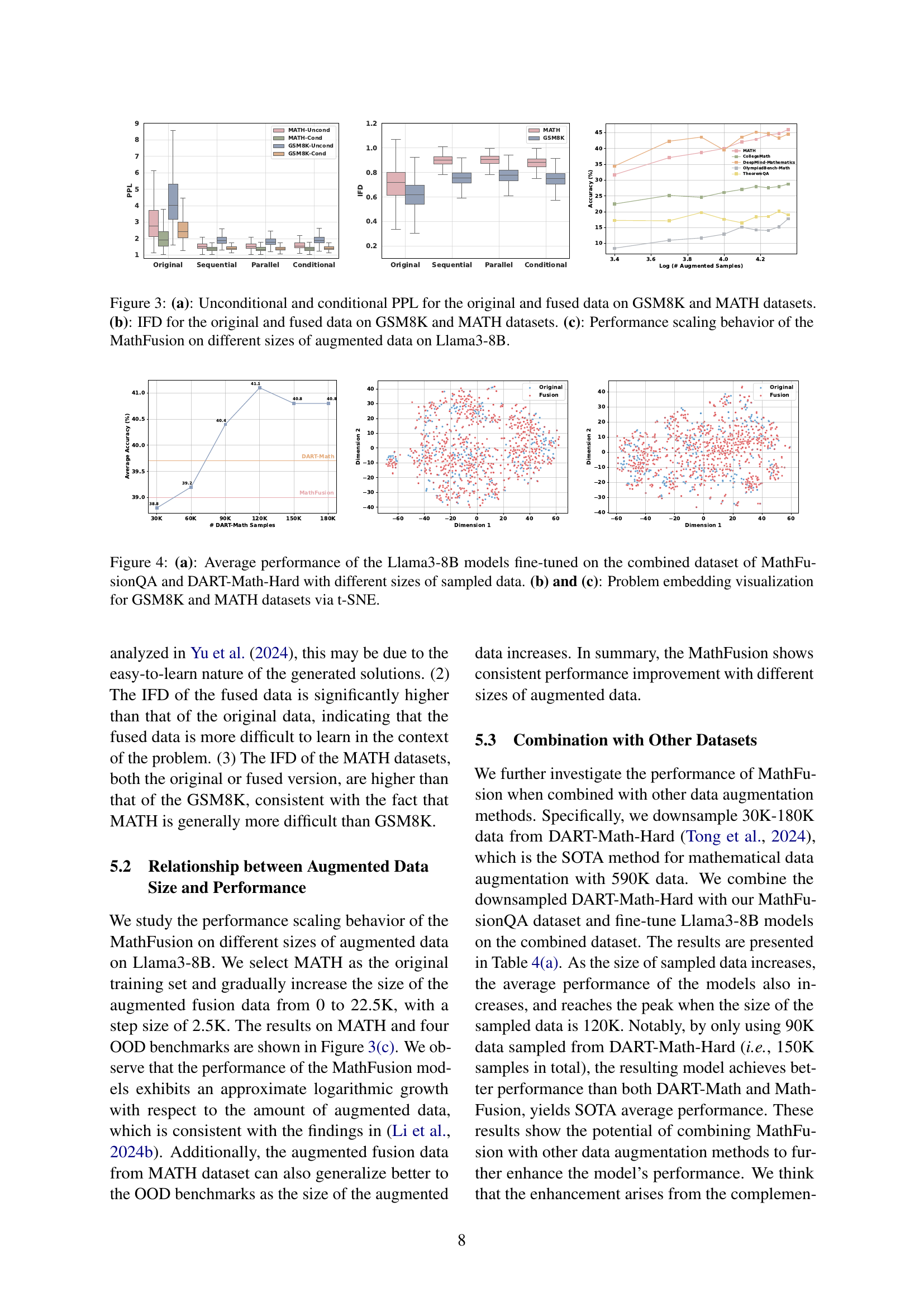
🔼 Figure 3 presents a tripartite analysis of the MathFusion model’s performance using Llama3-8B. Panel (a) compares the unconditional and conditional perplexity scores (PPL) for both original and fused datasets from GSM8K and MATH. Panel (b) shows the instruction-following difficulty (IFD) for the same datasets, providing insight into the relative challenge of each. Finally, panel (c) illustrates how model performance scales as the size of augmented data increases for the MathFusion model.
read the caption
Figure 3: (a): Unconditional and conditional PPL for the original and fused data on GSM8K and MATH datasets. (b): IFD for the original and fused data on GSM8K and MATH datasets. (c): Performance scaling behavior of the MathFusion on different sizes of augmented data on Llama3-8B.

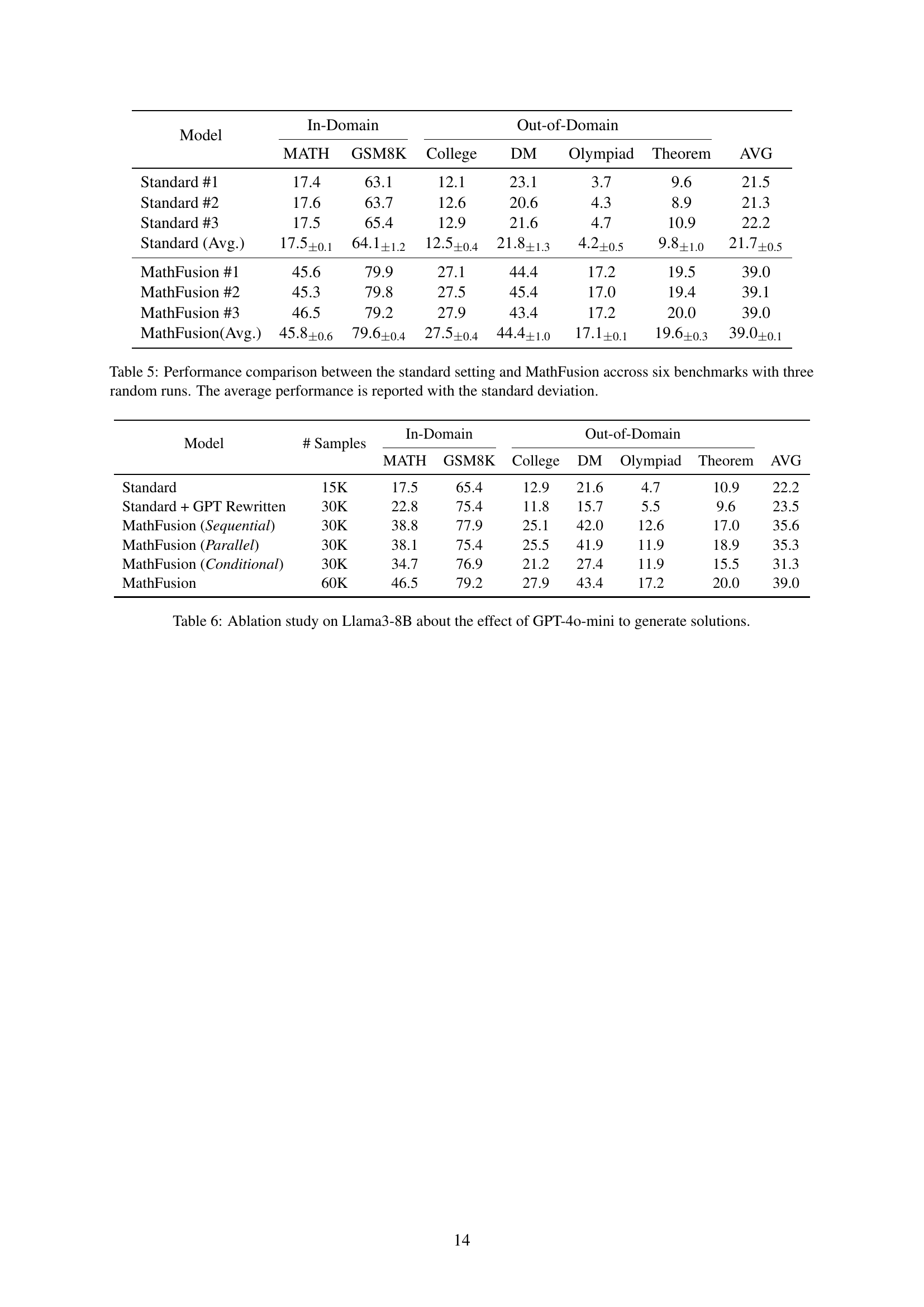
🔼 Figure 4(a) shows how the performance of Llama3-8B language models changes as the amount of training data increases. The models were trained on a combined dataset of MathFusionQA and DART-Math-Hard. The x-axis represents the size of the sampled data from this combined dataset. The y-axis shows the average performance across multiple benchmarks. Figures 4(b) and 4(c) use t-SNE to visualize how problems from the GSM8K and MATH datasets are represented in a lower-dimensional embedding space. This visualization helps to understand the relationships and similarities between the different problems in each dataset.
read the caption
Figure 4: (a): Average performance of the Llama3-8B models fine-tuned on the combined dataset of MathFusionQA and DART-Math-Hard with different sizes of sampled data. (b) and (c): Problem embedding visualization for GSM8K and MATH datasets via t-SNE.

🔼 This figure shows a pie chart visualizing the distribution of problem type combinations within the MATH dataset used in the paper. Each slice represents a pair of problem types combined using the MathFusion technique, and its size corresponds to the proportion of such pairings within the total dataset. The chart provides insight into the frequency with which various problem-type combinations were utilized during the data augmentation process. For example, a large slice for ‘(Algebra, Algebra)’ indicates that many problem pairs were created by combining two problems of the Algebra type.
read the caption
Figure 5: Distribution of combination types of problems in MATH dataset.
More on tables
| Model | # Samples | In-Domain | Out-of-Domain | |||||
| MATH | GSM8K | College | DM | Olympiad | Theorem | AVG | ||
| DeepSeekMath (7B Math-Specialized Base Model) | ||||||||
| DeepSeekMath-7B-RFT | 590K | 53.0 | 88.2 | 41.9 | 60.2 | 19.1 | 27.2 | 48.3 |
| DeepSeekMath-7B-DART-Math | 590K | 53.6 | 86.8 | 40.7 | 61.6 | 21.7 | 32.2 | 49.4 |
| DeepSeekMath-7B-Instruct | 780K | 46.9 | 82.7 | 37.1 | 52.2 | 14.2 | 28.1 | 43.5 |
| DeepSeekMath-7B-MMIQC | 2.3M | 45.3 | 79.0 | 35.3 | 52.9 | 13.0 | 23.4 | 41.5 |
| \hdashlineDeepSeekMath-7B-Standard | 15K | 30.6 | 66.3 | 22.7 | 28.6 | 5.6 | 11.0 | 27.5 |
| DeepSeekMath-7B-RefAug | 30K | 32.1 | 71.2 | 26.0 | 38.4 | 10.1 | 14.4 | 32.0 |
| MathFusion-DSMath-7B (Sequential) | 30K | 49.9 | 76.6 | 38.8 | 64.6 | 21.6 | 22.8 | 45.7 |
| MathFusion-DSMath-7B (Parallel) | 30K | 50.9 | 76.7 | 38.9 | 62.2 | 19.0 | 23.8 | 45.3 |
| MathFusion-DSMath-7B (Conditional) | 30K | 48.5 | 74.6 | 37.0 | 55.2 | 19.3 | 19.0 | 42.3 |
| DeepSeekMath-7B-MetaMath† | 60K | 40.0 | 79.0 | 33.2 | 45.9 | 9.5 | 18.9 | 37.8 |
| DeepSeekMath-7B-MMIQC† | 60K | 26.3 | 60.6 | 19.2 | 41.5 | 10.4 | 6.8 | 27.5 |
| DeepSeekMath-7B-RefAug† | 60K | 33.1 | 71.6 | 26.2 | 35.4 | 10.5 | 14.0 | 31.8 |
| DeepSeekMath-7B-DART-Math† | 60K | 51.4 | 82.9 | 39.1 | 62.8 | 21.0 | 27.4 | 47.4 |
| MathFusion-DSMath-7B | 60K | 53.4 | 77.9 | 39.8 | 65.8 | 23.3 | 24.6 | 47.5 |
| Mistral-7B (7-8B General Base Model) | ||||||||
| Mistral-7B-MetaMath | 400K | 29.8 | 76.5 | 19.3 | 28.0 | 5.9 | 14.0 | 28.9 |
| Mistral-7B-WizardMath-V1.1 | 418K | 32.3 | 80.4 | 23.1 | 38.4 | 7.7 | 16.6 | 33.1 |
| Mistral-7B-RFT | 590K | 38.7 | 82.3 | 24.2 | 35.6 | 8.7 | 16.2 | 34.3 |
| Mistral-7B-DART-Math | 590K | 45.5 | 81.1 | 29.4 | 45.1 | 14.7 | 17.0 | 38.8 |
| Mistral-7B-MathScale | 2.0M | 35.2 | 74.8 | 21.8 | – | – | – | – |
| Mistral-7B-MMIQC | 2.3M | 37.4 | 75.4 | 28.5 | 38.0 | 9.4 | 16.2 | 34.2 |
| \hdashlineMistral-7B-Standard | 15K | 12.4 | 60.3 | 8.4 | 17.0 | 2.2 | 7.6 | 18.0 |
| Mistral-7B-RefAug | 30K | 15.1 | 61.1 | 10.4 | 15.4 | 3.1 | 11.0 | 19.4 |
| MathFusion-Mistral-7B (Sequential) | 30K | 32.7 | 73.9 | 18.9 | 29.3 | 9.3 | 15.5 | 29.9 |
| MathFusion-Mistral-7B (Parallel) | 30K | 30.9 | 75.1 | 20.9 | 26.5 | 11.0 | 15.2 | 29.9 |
| MathFusion-Mistral-7B (Conditional) | 30K | 26.3 | 73.0 | 15.6 | 21.4 | 7.3 | 12.8 | 26.1 |
| Mistral-7B-MetaMath† | 60K | 22.7 | 70.8 | 14.1 | 27.2 | 5.0 | 12.2 | 25.3 |
| Mistral-7B-MMIQC† | 60K | 17.3 | 61.4 | 11.1 | 13.5 | 5.0 | 5.9 | 19.0 |
| Mistral-7B-RefAug† | 60K | 17.4 | 63.1 | 12.5 | 18.1 | 3.9 | 11.1 | 21.0 |
| Mistral-7B-DART-Math† | 60K | 34.1 | 77.2 | 23.4 | 36.0 | 8.7 | 18.2 | 32.9 |
| MathFusion-Mistral-7B | 60K | 41.6 | 79.8 | 24.3 | 39.2 | 13.6 | 18.1 | 36.1 |
| Llama3-8B (7-8B General Base Model) | ||||||||
| Llama3-8B-MetaMath | 400K | 32.5 | 77.3 | 20.6 | 35.0 | 5.5 | 13.8 | 30.8 |
| Llama3-8B-RFT | 590K | 39.7 | 81.7 | 23.9 | 41.7 | 9.3 | 14.9 | 35.2 |
| Llama3-8B-MMIQC | 2.3M | 39.5 | 77.6 | 29.5 | 41.0 | 9.6 | 16.2 | 35.6 |
| Llama3-8B-DART-Math | 590K | 46.6 | 81.1 | 28.8 | 48.0 | 14.5 | 19.4 | 39.7 |
| \hdashlineLlama3-8B-Standard | 15K | 17.5 | 65.4 | 12.9 | 21.6 | 4.7 | 10.9 | 22.2 |
| Llama3-8B-RefAug | 30K | 20.8 | 67.3 | 15.7 | 25.9 | 4.7 | 13.6 | 24.7 |
| MathFusion-Llama3-8B (Sequential) | 30K | 38.8 | 77.9 | 25.1 | 42.0 | 12.6 | 17.0 | 35.6 |
| MathFusion-Llama3-8B (Parallel) | 30K | 38.1 | 75.4 | 25.5 | 41.9 | 11.9 | 18.9 | 35.3 |
| MathFusion-Llama3-8B (Conditional) | 30K | 34.7 | 76.9 | 21.2 | 27.4 | 11.9 | 15.5 | 31.3 |
| Llama3-8B-MetaMath† | 60K | 28.7 | 78.5 | 19.7 | 31.3 | 5.3 | 16.1 | 29.9 |
| Llama3-8B-MMIQC† | 60K | 24.4 | 69.7 | 13.4 | 30.9 | 5.2 | 10.6 | 25.7 |
| Llama3-8B-RefAug† | 60K | 20.3 | 68.6 | 15.5 | 29.1 | 5.5 | 13.0 | 25.3 |
| Llama3-8B-DART-Math† | 60K | 39.6 | 82.2 | 27.9 | 39.9 | 12.9 | 22.9 | 37.6 |
| MathFusion-Llama3-8B | 60K | 46.5 | 79.2 | 27.9 | 43.4 | 17.2 | 20.0 | 39.0 |
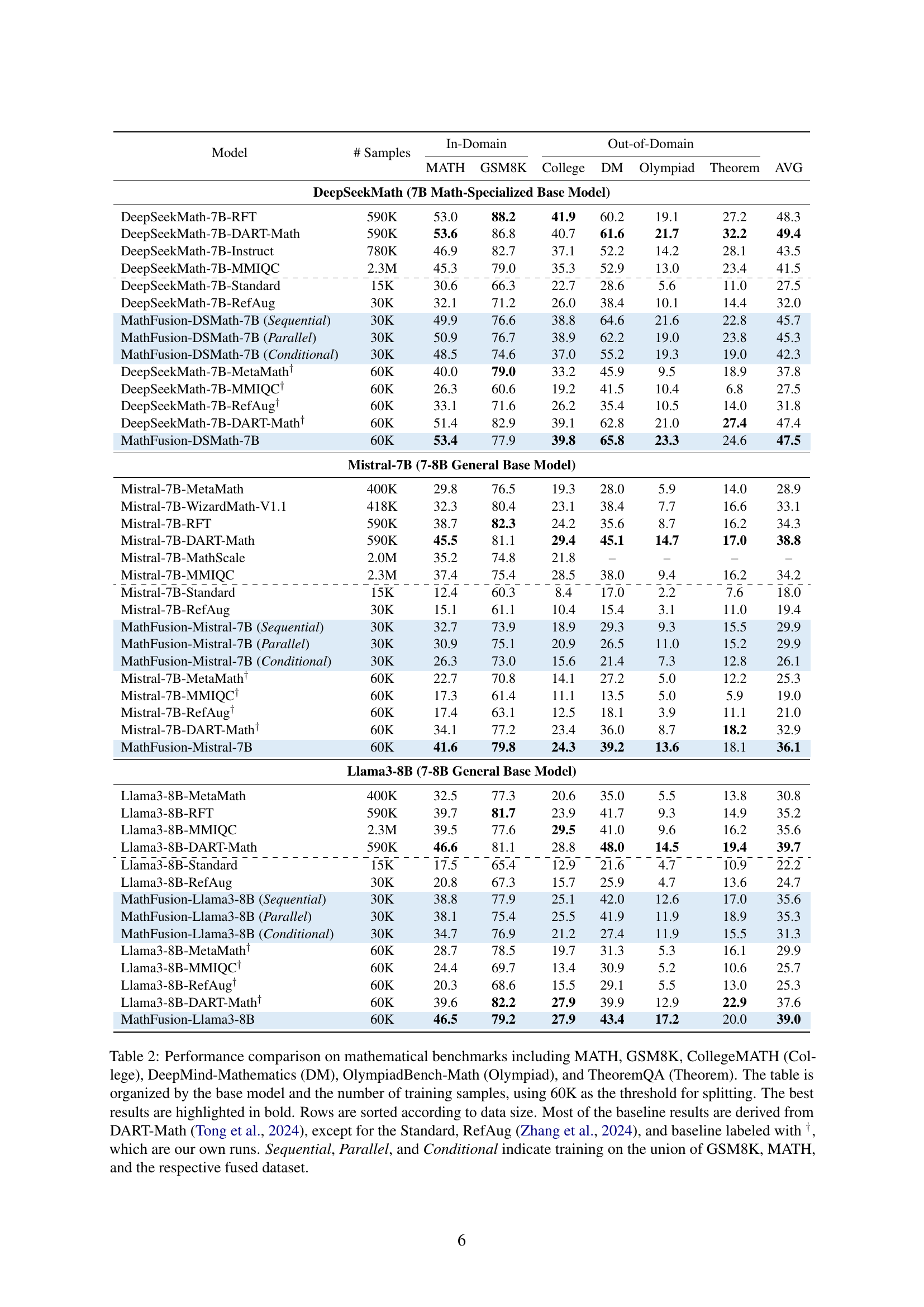
🔼 Table 2 presents a performance comparison of various Large Language Models (LLMs) on six mathematical reasoning benchmarks: MATH, GSM8K, CollegeMATH, DeepMind-Mathematics, OlympiadBench-Math, and TheoremQA. The table is organized to show the impact of different training data sizes and augmentation methods. Models are grouped by their base architecture (7B math-specialized or 7-8B general) and the amount of training data used (with 60K samples serving as a key division point). Results for MathFusion, along with several key comparative LLMs, are shown. The ‘Standard’ row indicates performance with minimal augmentation, while MathFusion results are broken down by fusion strategy (Sequential, Parallel, Conditional). Note that most baseline results come from the DART-Math paper, with some exceptions explicitly stated.
read the caption
Table 2: Performance comparison on mathematical benchmarks including MATH, GSM8K, CollegeMATH (College), DeepMind-Mathematics (DM), OlympiadBench-Math (Olympiad), and TheoremQA (Theorem). The table is organized by the base model and the number of training samples, using 60K as the threshold for splitting. The best results are highlighted in bold. Rows are sorted according to data size. Most of the baseline results are derived from DART-Math (Tong et al., 2024), except for the Standard, RefAug (Zhang et al., 2024), and baseline labeled with †, which are our own runs. Sequential, Parallel, and Conditional indicate training on the union of GSM8K, MATH, and the respective fused dataset.
| Method | Sequential | Parallel | Conditional | MATH | GSM8K |
| Standard | ✗ | ✗ | ✗ | 17.5 | 65.4 |
| MathFusion | ✗ | ✓ | ✓ | 42.6 | 78.2 |
| ✓ | ✗ | ✓ | 43.0 | 76.9 | |
| ✓ | ✓ | ✗ | 43.6 | 79.2 | |
| ✓ | ✓ | ✓ | 45.6 | 79.9 |
🔼 This table presents the results of an ablation study to evaluate the individual and combined effects of three different fusion strategies (sequential, parallel, and conditional) on the performance of a Llama3-8B language model in solving mathematical problems. The standard setting represents the baseline performance of the model without any fusion strategies. The table shows the accuracy achieved on two key benchmarks (MATH and GSM8K) by the model trained with different combinations of fusion strategies, offering insights into their individual and combined contributions to improved mathematical reasoning ability.
read the caption
Table 3: Effect of three fusion strategies on Llama3-8B.
| Dataset | GSM8K | MATH | Total |
| Standard | 7.5K | 7.5K | 15K |
| MathFusionQA (Sequential) | 15K | 15K | 30K |
| MathFusionQA (Parallel) | 15K | 15K | 30K |
| MathFusionQA (Conditional) | 15K | 15K | 30K |
| MathFusionQA | 30K | 30K | 60K |
🔼 Table 4 presents a detailed breakdown of the dataset sizes used in the study. It compares the number of samples in the original GSM8K and MATH datasets with the number of samples added through three different fusion strategies within the MathFusionQA dataset. The total number of samples in the final MathFusionQA dataset, which combines the original data with the augmented data from the three fusion strategies, is also provided.
read the caption
Table 4: Statistics of the MathFusionQA dataset and the original datasets GSM8K and MATH.
| Model | In-Domain | Out-of-Domain | |||||
| MATH | GSM8K | College | DM | Olympiad | Theorem | AVG | |
| Standard #1 | 17.4 | 63.1 | 12.1 | 23.1 | 3.7 | 9.6 | 21.5 |
| Standard #2 | 17.6 | 63.7 | 12.6 | 20.6 | 4.3 | 8.9 | 21.3 |
| Standard #3 | 17.5 | 65.4 | 12.9 | 21.6 | 4.7 | 10.9 | 22.2 |
| Standard (Avg.) | 17.50.1 | 64.11.2 | 12.50.4 | 21.81.3 | 4.20.5 | 9.81.0 | 21.70.5 |
| MathFusion #1 | 45.6 | 79.9 | 27.1 | 44.4 | 17.2 | 19.5 | 39.0 |
| MathFusion #2 | 45.3 | 79.8 | 27.5 | 45.4 | 17.0 | 19.4 | 39.1 |
| MathFusion #3 | 46.5 | 79.2 | 27.9 | 43.4 | 17.2 | 20.0 | 39.0 |
| MathFusion(Avg.) | 45.80.6 | 79.60.4 | 27.50.4 | 44.41.0 | 17.10.1 | 19.60.3 | 39.00.1 |
🔼 This table presents a performance comparison between a standard instruction-tuned LLM and three variants of the MathFusion model across six mathematical reasoning benchmarks. The MathFusion models incorporate different problem fusion strategies to enhance mathematical reasoning. The table shows the average accuracy and standard deviation across three random runs for each model on each benchmark. This allows for a quantitative assessment of the impact of the MathFusion techniques on model performance compared to a standard baseline.
read the caption
Table 5: Performance comparison between the standard setting and MathFusion accross six benchmarks with three random runs. The average performance is reported with the standard deviation.
| Model | # Samples | In-Domain | Out-of-Domain | |||||
| MATH | GSM8K | College | DM | Olympiad | Theorem | AVG | ||
| Standard | 15K | 17.5 | 65.4 | 12.9 | 21.6 | 4.7 | 10.9 | 22.2 |
| Standard + GPT Rewritten | 30K | 22.8 | 75.4 | 11.8 | 15.7 | 5.5 | 9.6 | 23.5 |
| MathFusion (Sequential) | 30K | 38.8 | 77.9 | 25.1 | 42.0 | 12.6 | 17.0 | 35.6 |
| MathFusion (Parallel) | 30K | 38.1 | 75.4 | 25.5 | 41.9 | 11.9 | 18.9 | 35.3 |
| MathFusion (Conditional) | 30K | 34.7 | 76.9 | 21.2 | 27.4 | 11.9 | 15.5 | 31.3 |
| MathFusion | 60K | 46.5 | 79.2 | 27.9 | 43.4 | 17.2 | 20.0 | 39.0 |
🔼 This table presents the results of an ablation study conducted to assess the impact of using GPT-4o-mini to generate solutions on the Llama3-8B model’s performance. It compares the model’s performance when trained with the standard training data, data augmented by GPT-4o-mini-generated solutions, and data augmented by the proposed MathFusion method. The comparison is done across multiple metrics on different benchmarks, including in-domain (MATH, GSM8K) and out-of-domain datasets (CollegeMath, DeepMind-Mathematics, OlympiadBench-Math, TheoremQA). The table helps to isolate the impact of the improved solution generation on the overall performance gains.
read the caption
Table 6: Ablation study on Llama3-8B about the effect of GPT-4o-mini to generate solutions.
Full paper#