Stop Overthinking: A Survey on Efficient Reasoning for Large Language Models

2503.16419

Yang Sui et el.

🤗 2025-03-21

TL;DR
#

Large Language Models (LLMs) show great skills in complex tasks, but their reasoning process can be inefficient, leading to unnecessary computational costs. This is due to “overthinking phenomenon”, where models generate lengthy reasoning steps. To address this, the survey explores the concept of efficient reasoning, which aims to optimize reasoning length while maintaining the model’s capabilities. Efficient reasoning seeks practical benefits like reduced costs and improved responsiveness.

This survey categorizes current approaches to achieving efficient reasoning in LLMs based on the inherent mechanism of LLMs: model-based, reasoning output-based, and input prompts-based strategies. It discusses efficient data for training, explores small language models, and covers evaluation methods. The authors maintain a public repository to track the research. This work aims to provide insights that can guide future research and the development of reasoning-driven applications.

Key Takeaways
#

Why does it matter?
#

This survey is important for researchers because it offers a structured overview of efficient reasoning, highlighting its impact on reducing computational costs and improving responsiveness. It opens avenues for exploration of efficient data and small models.

Visual Insights
#

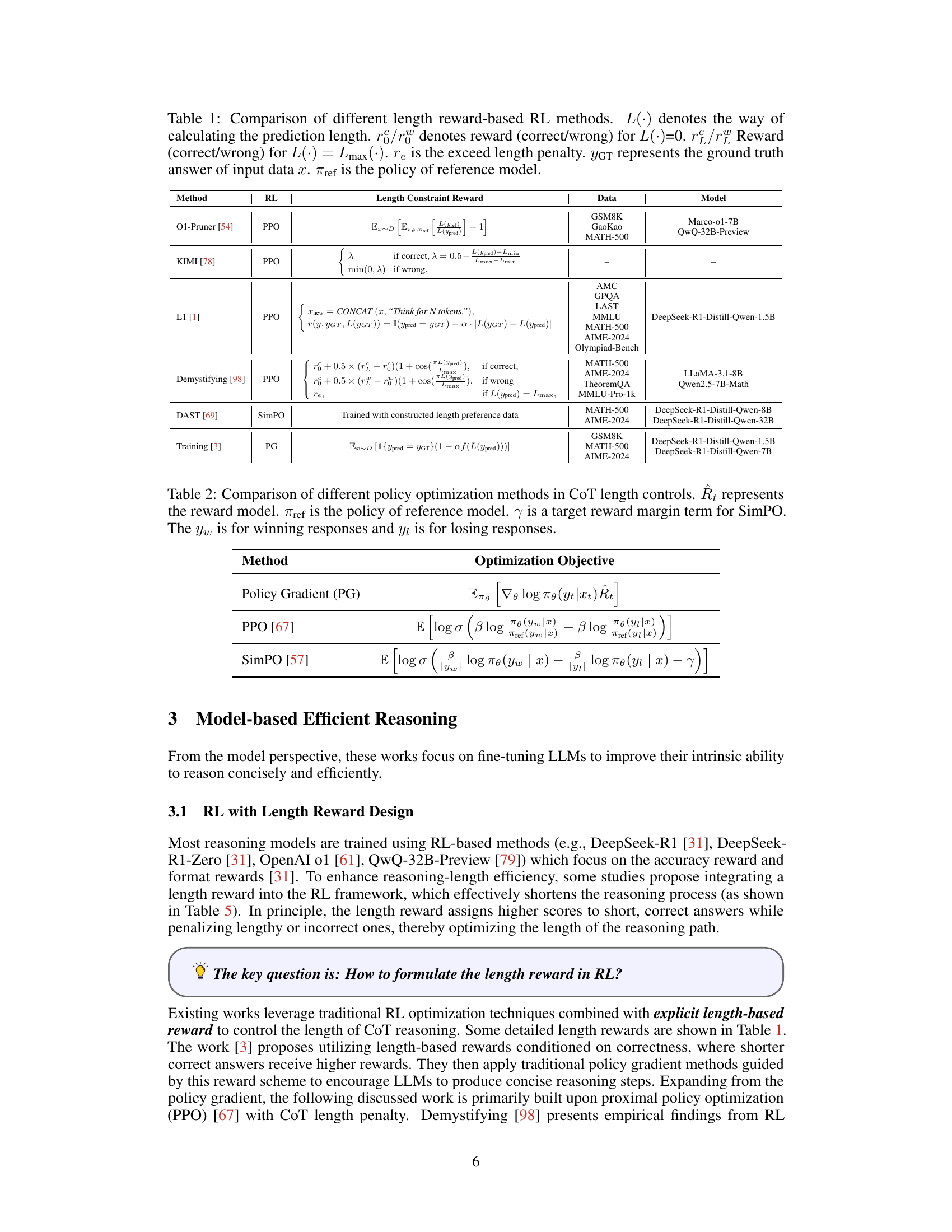
🔼 This figure illustrates the process of developing efficient reasoning in large language models (LLMs). It starts with a base LLM, which is then enhanced through supervised fine-tuning (SFT) and/or reinforcement learning (RL) to create a reasoning model. However, these reasoning models often produce excessively long reasoning chains, a phenomenon known as ‘overthinking’. To address this, various methods are employed to shorten the reasoning process while maintaining accuracy. These methods include reducing redundant steps in the reasoning output, optimizing the reasoning model itself, and designing prompts that guide the model towards more concise reasoning. The ultimate goal is to enable LLMs to answer questions effectively with concise and accurate reasoning steps.
read the caption
Figure 1: The pipeline of developing efficient reasoning for LLMs. A reasoning model can be trained on the base model using SFT, RL, or a combination of both. While reasoning models demonstrate strong reasoning capabilities, they often suffer from the “overthinking phenomenon”, generating unnecessarily lengthy reasoning steps. To improve efficiency, various methods can be applied to reduce redundant steps while maintaining accuracy, or to fine-tune non-reasoning models to incorporate efficient reasoning capabilities. This approach enables the model to answer questions with concise and effective reasoning steps. In this paper, we explore the latest progress in efficient reasoning for LLMs, aiming to provide insights that can guide future research and the development of reasoning-driven applications across various domains.

Method	RL	Length Constraint Reward	Data	Model
O1-Pruner [54]	PPO	$\mathbb{E}_{x\sim D}\left[\mathbb{E}_{\pi_{\theta},\pi_{\text{ref}}}\left[% \frac{L(y_{\text{ref}})}{L(y_{\text{pred}})}\right]-1\right]$	GSM8K GaoKao MATH-500	Marco-o1-7B QwQ-32B-Preview
KIMI [78]	PPO	$\begin{cases}\;\lambda&\!\text{if correct},\lambda=0.5\!-\!\frac{L(y_{\text{% pred}})-L_{\min}}{L_{\max}-L_{\min}}\\ \;\min(0,\lambda)&\!\text{if wrong}.\end{cases}$	–	–
L1 [1]	PPO	$\begin{cases}\;x_{\text{new}}=\textit{CONCAT}~{}(x,\textit{\textquotedblleft Think% for N tokens.\textquotedblright}),\\ \;r(y,y_{GT},L(y_{GT}))=\mathbb{I}(y_{\text{pred}}=y_{GT})-\alpha\cdot\|L(y_{GT% })-L(y_{\text{pred}})\|\end{cases}$	AMC GPQA LAST MMLU MATH-500 AIME-2024 Olympiad-Bench	DeepSeek-R1-Distill-Qwen-1.5B
Demystifying [98]	PPO	$\begin{cases}\;r_{0}^{c}+0.5\times(r_{L}^{c}-r_{0}^{c})(1+\cos({\frac{\pi L(y_% {\text{pred}})}{L_{\max}}}),&\text{if correct},\\ \;r_{0}^{c}+0.5\times(r_{L}^{w}-r_{0}^{w})(1+\cos({\frac{\pi L(y_{\text{pred}}% )}{L_{\max}}}),&\text{if wrong}\\ \;r_{e},&\text{if }L(y_{\text{pred}})=L_{\max},\end{cases}$	MATH-500 AIME-2024 TheoremQA MMLU-Pro-1k	LLaMA-3.1-8B Qwen2.5-7B-Math
DAST [69]	SimPO	Trained with constructed length preference data	MATH-500 AIME-2024	DeepSeek-R1-Distill-Qwen-8B DeepSeek-R1-Distill-Qwen-32B
Training [3]	PG	$\mathbb{E}_{x\sim D}\left[\mathbf{1}\{y_{\text{pred}}=y_{\text{GT}}\}(1-\alpha f% (L(y_{\text{pred}})))\right]$	GSM8K MATH-500 AIME-2024	DeepSeek-R1-Distill-Qwen-1.5B DeepSeek-R1-Distill-Qwen-7B

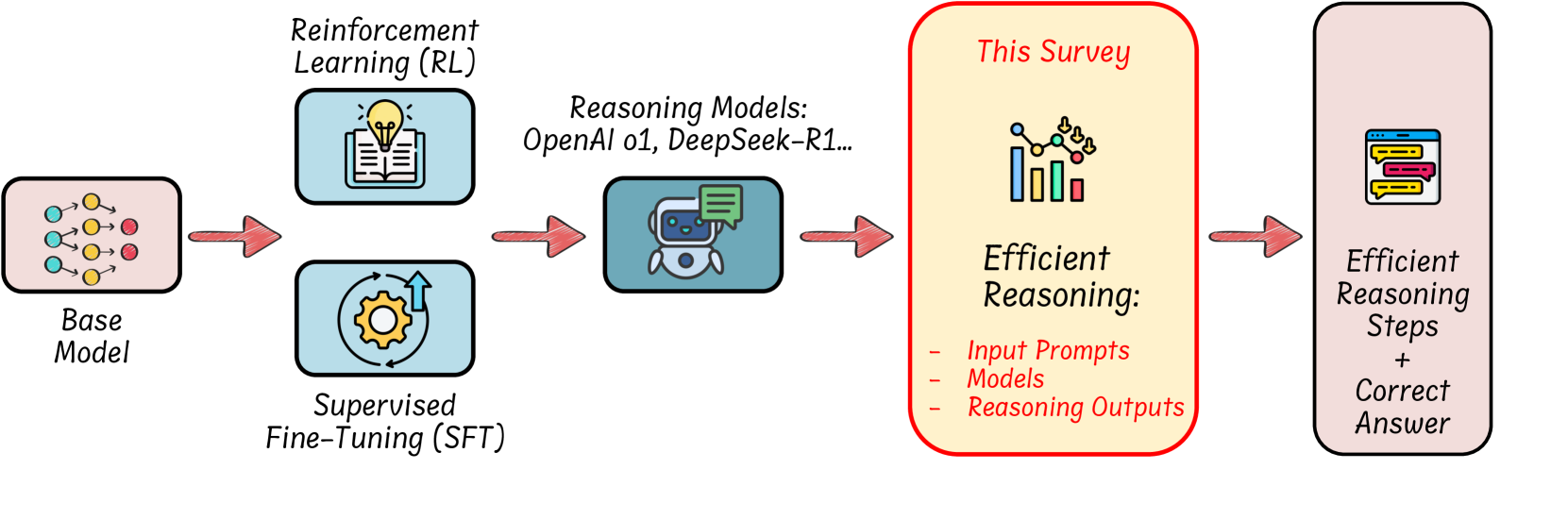
🔼 Table 1 compares several reinforcement learning (RL) methods used to optimize the length of chain-of-thought (CoT) reasoning in large language models (LLMs). It details the reward structures used in each method, specifying how rewards are assigned based on whether the model’s response is correct or incorrect, and the length of the response relative to the optimal or minimum length. The table also lists the datasets and LLMs used in the experiments for each method. The different reward components help to balance accuracy and brevity, encouraging shorter, accurate responses. Note that L(⋅) represents the length calculation method, r0c/r0w are the correct/wrong rewards when the response is at minimum length and rLc/rLw are the correct/wrong rewards for the maximum length; re is an additional penalty for exceeding the maximum length, YGT is the ground-truth answer, and πref is the policy of the reference model.
read the caption
Table 1: Comparison of different length reward-based RL methods. L⁢(⋅)𝐿⋅L(\cdot)italic_L ( ⋅ ) denotes the way of calculating the prediction length. r0c/r0wsuperscriptsubscript𝑟0𝑐superscriptsubscript𝑟0𝑤r_{0}^{c}/r_{0}^{w}italic_r start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_c end_POSTSUPERSCRIPT / italic_r start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_w end_POSTSUPERSCRIPT denotes reward (correct/wrong) for L⁢(⋅)𝐿⋅L(\cdot)italic_L ( ⋅ )=0. rLc/rLwsuperscriptsubscript𝑟𝐿𝑐superscriptsubscript𝑟𝐿𝑤r_{L}^{c}/r_{L}^{w}italic_r start_POSTSUBSCRIPT italic_L end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_c end_POSTSUPERSCRIPT / italic_r start_POSTSUBSCRIPT italic_L end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_w end_POSTSUPERSCRIPT Reward (correct/wrong) for L⁢(⋅)=Lmax⁢(⋅)𝐿⋅subscript𝐿max⋅L(\cdot)=L_{\text{max}}(\cdot)italic_L ( ⋅ ) = italic_L start_POSTSUBSCRIPT max end_POSTSUBSCRIPT ( ⋅ ). resubscript𝑟𝑒r_{e}italic_r start_POSTSUBSCRIPT italic_e end_POSTSUBSCRIPT is the exceed length penalty. yGTsubscript𝑦GTy_{\text{GT}}italic_y start_POSTSUBSCRIPT GT end_POSTSUBSCRIPT represents the ground truth answer of input data x𝑥xitalic_x. πrefsubscript𝜋ref\pi_{\text{ref}}italic_π start_POSTSUBSCRIPT ref end_POSTSUBSCRIPT is the policy of reference model.

In-depth insights
#

Overthinking LLMs
#

Overthinking in LLMs highlights the phenomenon where models generate unnecessarily detailed or redundant reasoning steps, hindering efficiency. This is particularly evident in smaller, reasoning-capable LLMs, leading to verbose outputs. It stems from the models’ tendency to produce extensive reasoning, even when a concise solution is achievable. It impairs problem-solving efficiency, potentially causing token budget overruns or even incorrect answers due to accumulated errors. Addressing overthinking is significant because pre-training recipes often encourage extended reasoning to improve accuracy, making it a design challenge to balance capability and efficiency. It also affects real-world applications and increases computational overheads.

RL Length Reward
#

RL with Length Reward is a compelling approach to enhance reasoning efficiency. By integrating length as a reward signal, the model is incentivized to produce concise, yet accurate solutions. This method combats overthinking and promotes efficient computation. The careful formulation of length reward is key: scoring short, correct answers highly, while penalizing lengthier or incorrect responses. It’s a balancing act between thorough reasoning and succinctness. Challenges involve defining appropriate reward functions and ensuring that length reduction doesn’t compromise accuracy. Fine-tuning the reward mechanism is vital to achieving optimal results in RL.

CoT Data Shortening
#

CoT data shortening focuses on creating more efficient reasoning by reducing the length of Chain-of-Thought examples. This can be achieved through methods like distilling knowledge from longer CoT examples into shorter ones, or directly generating concise CoT data. The goal is to maintain accuracy while minimizing computational cost and redundancy. The methods often incorporate prompt engineering or fine-tuning techniques to encourage models to produce succinct and effective reasoning steps. This contrasts with methods which emphasize extending reasoning paths, aiming for a balance between thoroughness and efficiency.

Latent Reasoning
#

Latent reasoning emphasizes extracting implicit knowledge representations. Rather than relying on explicit, step-by-step reasoning chains, the focus is on encoding reasoning processes into a compact, hidden space. This can lead to more efficient and flexible reasoning, as the model doesn’t need to generate verbose intermediate steps. By working in a compressed space, models can potentially achieve faster inference and better handle complex tasks. However, a key challenge is effectively training models to learn and utilize these latent representations, ensuring that the essential reasoning information is captured without explicit supervision.

Efficient Prompts
#

Efficient prompts are crucial for optimizing LLM performance. They involve crafting concise instructions to guide LLMs toward desired outputs. Effective prompts reduce reasoning steps, conserve resources, and improve accuracy. Methods include token budgeting and chain-of-draft prompting. These techniques explicitly instruct LLMs to be concise. Token budget constraints limit reasoning tokens. Chain-of-draft combines step-by-step reasoning with policies against verbosity. Some methods involve fine-tuning post prompting for performance gains. Attribute-driven reasoning dynamically directs language models based on the complexity of the prompt. Ideally, routing models assign simpler prompts to low-latency, efficient LLMs and complex prompts to strong, higher-latency LLMs, improving efficiency by managing resources.

More visual insights
#

More on figures

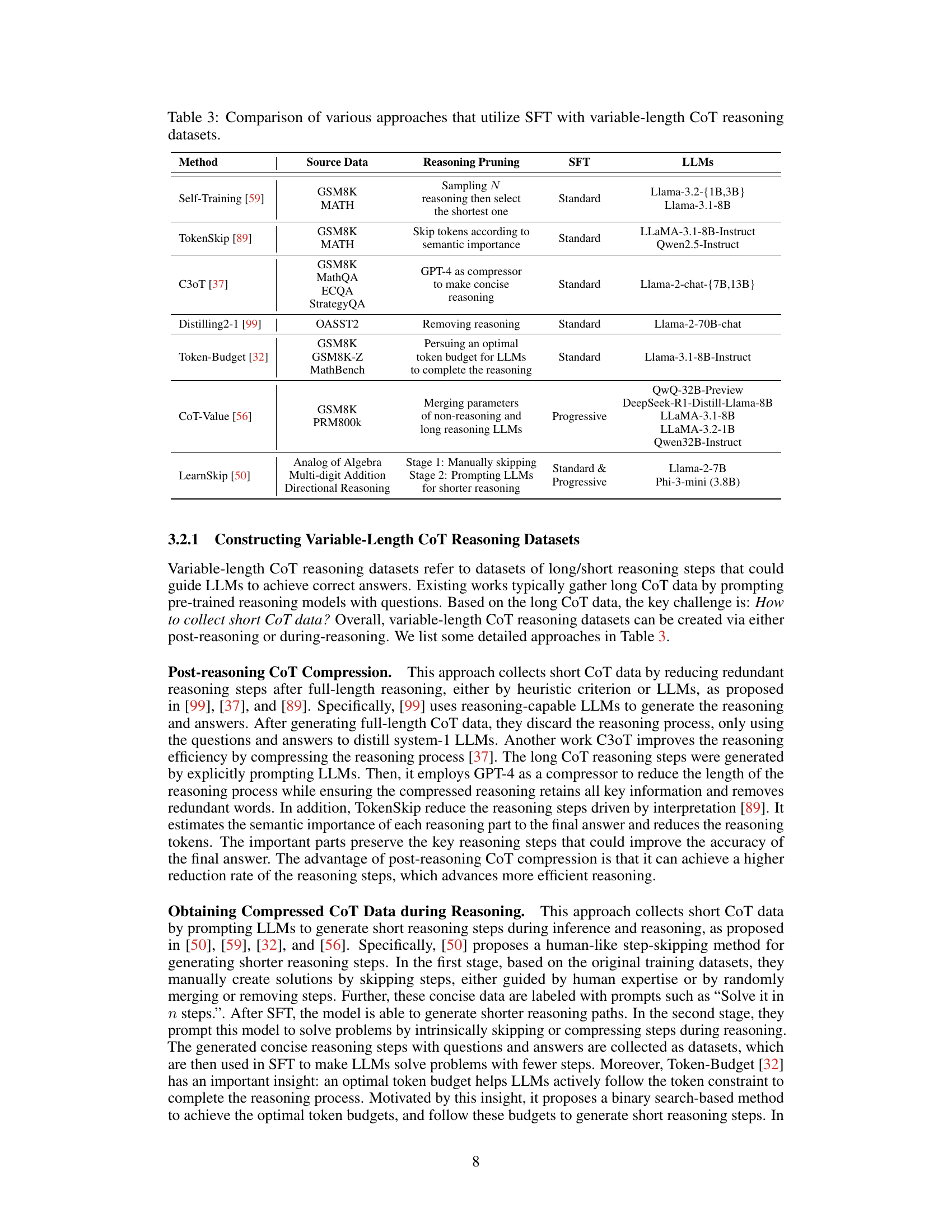
🔼 This figure categorizes efficient reasoning methods for large language models (LLMs) into three main categories based on their approach: model-oriented, reasoning output-oriented, and input prompts-oriented. Model-oriented methods focus on modifying the model architecture or training process to promote efficient reasoning. Reasoning output-oriented methods aim to optimize the reasoning process during inference by manipulating the output. Input prompts-oriented methods leverage carefully designed input prompts to guide the LLM toward more efficient reasoning. Each category further breaks down into specific techniques, illustrated in the figure with detailed section references from the paper. The model-oriented methods include reinforcement learning with length reward design and supervised fine-tuning with variable-length Chain-of-Thought (CoT) data. The reasoning output-oriented methods cover compressing reasoning steps into fewer latent representations and the dynamic reasoning paradigm during inference. Finally, the input prompts-oriented methods encompass prompt-guided efficient reasoning and routing prompts to optimize reasoning efficiency.
read the caption
Figure 2: Overview of efficient reasoning methods, which can be summarized as model-oriented (Left: I, II) and reasoning output-oriented (Middle: III, IV), and input prompts-oriented (Right: V, VI) methods. Specifically, (I) Reinforcement Learning with Length Reward Design (Section 3.1); (II) Supervised Fine-Tuning with Variable-Length CoT Data (Section 3.2); (III) Compressing Reasoning Steps into Fewer Latent Representation (Section 4.1); (IV) Dynamic Reasoning Paradigm during Inference (Section 4.2); (V) Prompt-guided Efficient Reasoning (Section 5.1); (VI) Routing Prompts to Optimize Reasoning Efficiency (Section 5.2);

🔼 This figure presents a taxonomy of existing research on efficient reasoning methods for Large Language Models (LLMs). It categorizes the existing works into three main approaches: model-based efficient reasoning (optimizing model architecture or training directly for conciseness), reasoning output-based efficient reasoning (dynamically adjusting reasoning steps during inference), and input prompt-based efficient reasoning (leveraging prompt properties to influence reasoning efficiency). Within each category are further sub-categories representing specific techniques or methods, providing a structured overview of the landscape of efficient reasoning research in LLMs.
read the caption
Figure 3: Taxonomy of existing literature on efficient reasoning for LLMs.

🔼 The figure showcases the overthinking phenomenon in large language models (LLMs). It presents two examples of LLMs, QwQ-32B and DeepSeek-R1, attempting to answer the simple question: ‘Which is larger, 0.9 or 0.11?’ Both models produce verbose and lengthy reasoning processes before arriving at the correct answer, taking 19 and 42 seconds, respectively. This demonstrates the inefficiency of these LLMs, as they expend significant computational resources on redundant steps, highlighting the need for efficient reasoning techniques. The test was conducted in March 2025.
read the caption
Figure 4: An example of the “overthinking phenomenon”: when the reasoning model is asked “Which is larger, 0.9 or 0.11?”, it takes an unnecessarily long time (i.e., 19 seconds for QwQ-32B [79] and 42 seconds for DeepSeek-R1 [31]) to deliver its final answer. The example was tested in March 2025.

🔼 This figure illustrates the reinforcement learning (RL) approach used to train large language models (LLMs) for efficient reasoning. The key modification is incorporating a ’length reward’ into the RL training process. This reward mechanism incentivizes the model to produce shorter, correct answers by assigning higher rewards to such outputs, while penalizing longer or incorrect responses. The goal is to train LLMs that can effectively reason with conciseness without sacrificing accuracy, thus achieving efficient reasoning capabilities.
read the caption
Figure 5: Illustration of the method for RL fine-tuning with length reward designs. In principle, the length reward assigns higher rewards to short, correct answers and penalizes lengthy or wrong answers to achieve efficient reasoning LLMs.

🔼 This figure illustrates the process of using supervised fine-tuning (SFT) with variable-length chain-of-thought (CoT) reasoning datasets to improve the efficiency of reasoning in large language models (LLMs). It shows that both long and short CoT data are used in the training, resulting in a more efficient reasoning model. The process involves constructing variable-length datasets (through various methods described in the paper), followed by fine-tuning an LLM using these datasets. The goal is to teach the LLM to generate concise and effective reasoning steps without compromising accuracy.
read the caption
Figure 6: Illustration of methods for utilizing SFT with variable-length CoT reasoning datasets.

🔼 This figure compares different methods for compressing reasoning steps in large language models (LLMs) into fewer latent representations. It illustrates three different approaches: (1) Coconut uses continuous representations and trains the LLM gradually to incorporate these latent representations into its reasoning process. (2) CODI employs self-distillation to learn latent representations. (3) CCOT compresses full CoT reasoning steps into a smaller set of compressed tokens which a separate decoding module utilizes to reconstruct concise reasoning. The figure visually shows the architecture and data flow for each method, highlighting their similarities and differences in how they compress reasoning steps.
read the caption
Figure 7: Comparison of methods of compressing reasoning steps into fewer latent representations.

More on tables

Method	Optimization Objective
Policy Gradient (PG)	$\mathbb{E}_{\pi_{\theta}}\left[\nabla_{\theta}\log\pi_{\theta}(y_{t}\|x_{t})% \hat{R}_{t}\right]$
PPO [67]	$\mathbb{E}\left[\log\sigma\left(\beta\log\frac{\pi_{\theta}(y_{w}\mid x)}{\pi_% {\text{ref}}(y_{w}\mid x)}-\beta\log\frac{\pi_{\theta}(y_{l}\mid x)}{\pi_{% \text{ref}}(y_{l}\mid x)}\right)\right]$
SimPO [57]	$\mathbb{E}\left[\log\sigma\left(\frac{\beta}{\|y_{w}\|}\log\pi_{\theta}(y_{w}% \mid x)-\frac{\beta}{\|y_{l}\|}\log\pi_{\theta}(y_{l}\mid x)-\gamma\right)\right]$

🔼 Table 2 details the policy optimization methods used to control the length of Chain-of-Thought (CoT) reasoning in large language models (LLMs). It compares different methods (PPO and SimPO), showing their policy gradient calculation and optimization objective functions. The table clarifies the variables used in these functions: 𝑅𝑡 ̂R_t represents the reward model at time step t, πref π_ref denotes the reference model’s policy, γ γ represents a target reward margin for SimPO, 𝑦𝑤 y_w represents the reward for winning responses, and 𝑦𝑙 y_l is the reward for losing responses. This information helps to understand the specific algorithms and reward structures used in different approaches to making LLMs generate more concise reasoning chains.
read the caption
Table 2: Comparison of different policy optimization methods in CoT length controls. R^tsubscript^𝑅𝑡\hat{R}_{t}over^ start_ARG italic_R end_ARG start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT represents the reward model. πrefsubscript𝜋ref\pi_{\text{ref}}italic_π start_POSTSUBSCRIPT ref end_POSTSUBSCRIPT is the policy of reference model. γ𝛾\gammaitalic_γ is a target reward margin term for SimPO. The ywsubscript𝑦𝑤y_{w}italic_y start_POSTSUBSCRIPT italic_w end_POSTSUBSCRIPT is for winning responses and ylsubscript𝑦𝑙y_{l}italic_y start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT is for losing responses.

Method	Source Data	Reasoning Pruning	SFT	LLMs
Self-Training [59]	GSM8K MATH	Sampling $N$ reasoning then select the shortest one	Standard	Llama-3.2-{1B,3B} Llama-3.1-8B
TokenSkip [89]	GSM8K MATH	Skip tokens according to semantic importance	Standard	LLaMA-3.1-8B-Instruct Qwen2.5-Instruct
C3oT [37]	GSM8K MathQA ECQA StrategyQA	GPT-4 as compressor to make concise reasoning	Standard	Llama-2-chat-{7B,13B}
Distilling2-1 [99]	OASST2	Removing reasoning	Standard	Llama-2-70B-chat
Token-Budget [32]	GSM8K GSM8K-Z MathBench	Persuing an optimal token budget for LLMs to complete the reasoning	Standard	Llama-3.1-8B-Instruct
CoT-Value [56]	GSM8K PRM800k	Merging parameters of non-reasoning and long reasoning LLMs	Progressive	QwQ-32B-Preview DeepSeek-R1-Distill-Llama-8B LLaMA-3.1-8B LLaMA-3.2-1B Qwen32B-Instruct
LearnSkip [50]	Analog of Algebra Multi-digit Addition Directional Reasoning	Stage 1: Manually skipping Stage 2: Prompting LLMs for shorter reasoning	Standard & Progressive	Llama-2-7B Phi-3-mini (3.8B)

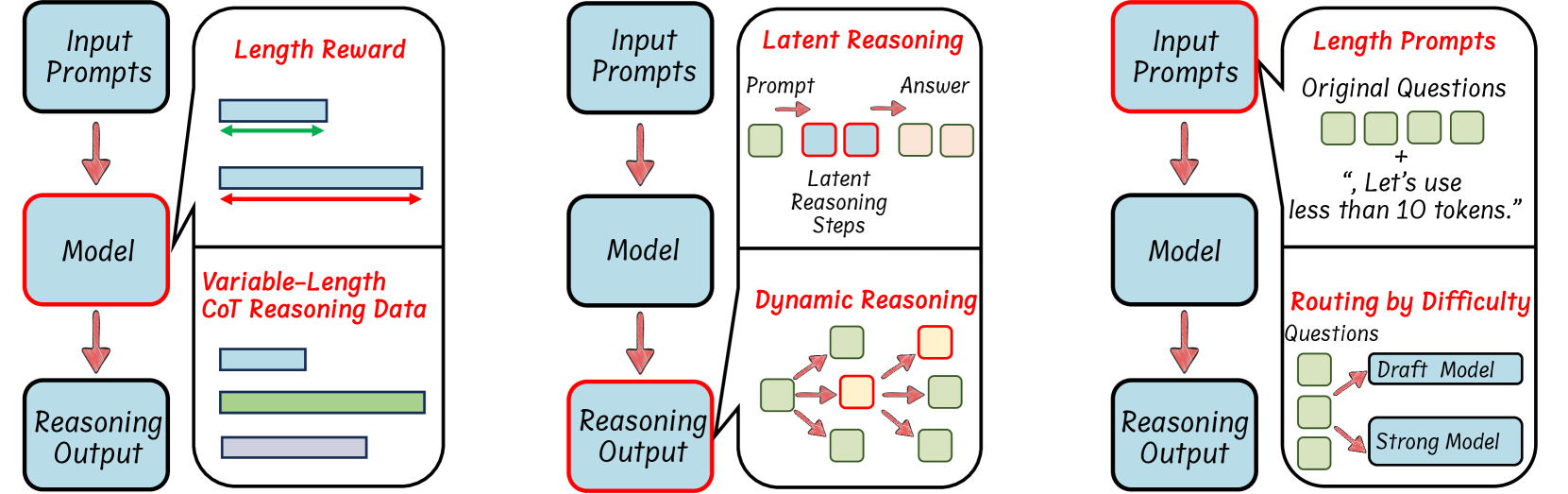
🔼 This table compares different methods that use supervised fine-tuning (SFT) with variable-length Chain-of-Thought (CoT) reasoning datasets to improve the efficiency of large language models (LLMs). It details the source data used for training, the reasoning pruning techniques employed (if any), the specific SFT method used, and the resulting LLMs.
read the caption
Table 3: Comparison of various approaches that utilize SFT with variable-length CoT reasoning datasets.

Category	Method	Training-free?	Baseline and Its Drawbacks	Method Description
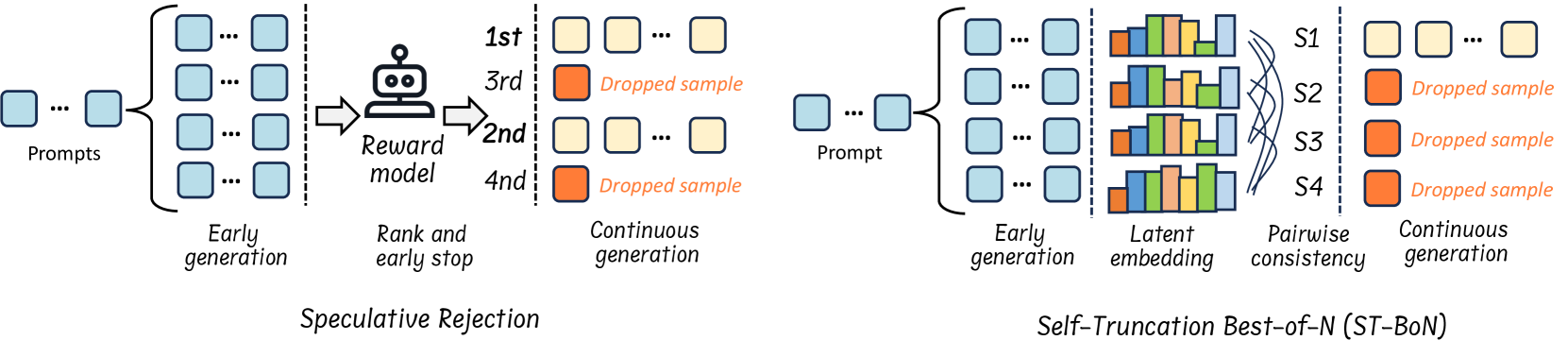
Reward-guided Efficient Reasoning	Speculative Rejection [76]	Yes	Best-of-N (BoN) Decoding: underutilizes GPU memory and computational resources during the early stages, leading to lower final rewards.	Starts BoN with a large initial batch size and rejects unpromising sequences periodically, efficiently achieving higher rewards.
Reward-guided Efficient Reasoning	Reward-Guided Speculative Decoding (RSD) [45]	Yes	Speculative Decoding: strictly enforces unbiasedness, discarding useful intermediate outputs and leading to computational inefficiency.	A speculative decoding method that leverages a reward model (PRM) to selectively accept high-quality outputs from a lightweight draft model, reducing computation while preserving accuracy.
Confidence/ Certainty-based Adaptive Reasoning	Dynamic Parallel Tree Search [24]	Yes	Tree-of-Thoughts: difficult to parallelize due to frequent switching of reasoning focus, and inefficient because of redundant exploration of suboptimal solutions	Dynamically parallelizes node expansion through adaptive batching and implements a search-and-transition mechanism (including Early Stop and Deep Seek) to prune unpromising paths early.
	Dynasor (Certaindex-based Scheduling) [28]	Yes	Serving systems with uniform resource allocation: allocate compute uniformly, leading to inefficient resource usage and unmet latency targets	Dynamically allocates compute for reasoning queries based on Certaindex, a statistical measure of reasoning progress, to maximize accuracy within resource constraints.
	FastMCTS [41]	Yes	Rejection Sampling: inefficient, discards intermediate steps, and fails to balance problem difficulty	An MCTS-inspired sampling strategy that efficiently generates high-quality multi-step reasoning data, providing step-level evaluation signals and balanced sampling across problem difficulties.
	Length-filtered Vote [88]	Yes	Majority Voting: ignores reasoning quality, includes suboptimal CoT lengths, and suffers from noisy predictions	A voting strategy that selects answers with the optimal CoT length by filtering out excessively short or long reasoning paths.
Consistency-based Selective Reasoning	Self-Truncation Best-of-N (ST-BoN) [85]	Yes	Best-of-N Sampling: fully generates all samples and relies on costly reward models	Estimates the most promising sample early via internal embedding consistency, truncating inferior samples prematurely.
Summarization-based Dynamic Reasoning	LightThinker [101]	No	Chain-of-Thought (CoT): high memory and computational overhead due to the generation of an excessive number of tokens	Trains LLMs to learn when and how to compress intermediate thoughts, condensing long reasoning chains into gist tokens, and uses a sparse-patterned attention mask during inference to enhance computational efficiency.
Summarization-based Dynamic Reasoning	InftyThink [94]	No	Monolithic Reasoning: reasoning output is verbose, and can quickly exceed the context window limit of the LLM, resulting in poor performance	An iterative reasoning paradigm that interleaves reasoning steps with intermediate summarization, enabling unbounded reasoning depth without architectural modifications.

🔼 This table compares various methods for dynamic reasoning during inference, focusing on their efficiency in terms of test-time computation. It categorizes methods by whether they are training-free, the specific criteria used to guide reasoning (e.g., reward, confidence, consistency), and provides a brief description of each method along with its advantages and disadvantages regarding computational efficiency and accuracy.
read the caption
Table 4: Comparison of different methods of dynamic reasoning paradigm of test time compute during inference.

Method	Prompt
TALE-EP [32]	Budget Estimation: (…) Task: Analyze the given question and estimate the minimum number of tokens required to generate a complete and accurate response. Please give the response by strictly following this format: [[budget]], for example, Budget: [[12]].
	Token-budget-aware CoT: Please answer the above question. Let’s think step by step and use less than <Token-Budget> tokens.
CoD [92]	Think step by step, but only keep a minimum draft for each thinking step, with 5 words at most. Return the answer at the end of the response after a separator ####.
CCoT [65]	Be concise.
Token Complexity [40]	BulletPoints (…) only use bullet points.
	OnlyNumbers (…) only use numbers or equations.
	NoSpaces (…) do not use any spaces or line breaks.
	NoProperGrammar (…) do not use proper grammar.
	AbbreviateWords (…) abbreviate words as much as possible.
	WordLimit(k) (…) use at most $k$ words. $k\in\{1,\dots,100\}$
	CharLimit(k) (…) use at most $k$ letters. $k\in\{1,\dots,500\}$
	TokenLimit(k) (…) use at most $k$ tokens. $k\in\{1,\dots,500\}$
	StepLimit(k) (…) use at most $k$ steps. $k\in\{1,\dots,5\}$
	ChineseCoT (…) Respond in Chinese
	ChineseCoT(k) (…) Use at most $k$ Chinese characters. $k\in\{1,\dots,500\}$

🔼 Table 5 presents various prompt engineering techniques to guide Large Language Models (LLMs) towards generating concise reasoning outputs. It details specific prompt modifications designed to control the length and detail of the reasoning process while maintaining accuracy. Each prompt type is listed along with a short explanation of its approach to concise reasoning.
read the caption
Table 5: A summary of prompts used with reasoning models to generate concise reasoning outputs. For further details, refer to Section 5.1.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Overthinking LLMs#

RL Length Reward#

CoT Data Shortening#

Latent Reasoning#

Efficient Prompts#

More visual insights#

Full paper#