Tokenize Image as a Set

2503.16425

Zigang Geng et el.

🤗 2025-03-21

TL;DR
#

Contemporary visual generation faces challenges with fixed compression ratios, leading to inefficient coding, especially in regions with varying semantic complexity. Current tokenization methods generate serialized codes with fixed positional correspondence, allocating the same number of codes to both simplistic and semantically dense regions. This raises a fundamental question of whether visually simplistic regions should receive the same representational capacity as semantically rich areas.

This paper introduces TokenSet, a fundamentally new paradigm for image generation through set-based tokenization and distribution modeling. It proposes to tokenize images into unordered sets to enable dynamic attention allocation based on regional semantic complexity. The dual transformation mechanism converts sets into fixed-length integer sequences with summation constraints. Fixed-Sum Discrete Diffusion addresses the challenge of modeling discrete sets and enables effective set distribution modeling.

Key Takeaways
#

Why does it matter?
#

This paper introduces a novel image generation framework, TokenSet, offering dynamic token allocation and enhanced robustness. This work can inspire more research to explore the non-serialized visual representation and generative model.

Visual Insights
#

🔼 This figure illustrates the pipeline of the proposed Tokenize Image as a Set method. It begins with an image encoder that transforms image patches into an unordered set of tokens (TokenSet). A dual transformation mechanism converts this set into a fixed-length integer sequence with a summation constraint. This sequence is then processed by a novel Fixed-Sum Discrete Diffusion model, which ensures the model respects the summation constraint throughout the diffusion process. Finally, an image decoder reconstructs the image from the resulting sequence.
read the caption
Figure 1: Pipeline of our method.

Order	Original	Reversed	Shuffled	Ascending	Descending
rFID $\downarrow$	$3.62$	$3.62$	$3.62$	$3.62$	$3.62$

🔼 This table presents the Fréchet Inception Distance (FID) scores for reconstructed images using different decoding orders of the tokens. The consistent FID scores across all orders demonstrate that the image reconstruction is invariant to the order of tokens used. This validates the permutation-invariance property claimed for the proposed tokenizer, ensuring that the model is robust against the order of tokens during inference.
read the caption
Table 1: Quantitative results of reconstructed images using tokens in different decoding orders. The identical rFID across all orders confirms the permutation-invariance property of our tokenizer.

In-depth insights
#

Set-based Tokens
#

Set-based tokens offer a new perspective on image representation by treating images as unordered collections of visual elements. This approach contrasts sharply with traditional methods that serialize images into fixed-position latent codes. The key advantage lies in dynamically allocating coding capacity based on regional semantic complexity. Instead of uniformly compressing the entire image, set-based tokens enable the model to focus on semantically rich areas, allocating more tokens where needed. This leads to better global context aggregation, as the model can prioritize important regions and reduce redundancy in simpler areas. Moreover, set-based tokens exhibit improved robustness to local perturbations, since the absence of fixed positional correspondence makes the model less sensitive to noise and minor variations in the input image. The permutation invariance is also an important feature.

Fixed-Sum Models
#

The ‘Fixed-Sum’ models likely address a key challenge in set-based representation learning: ensuring the sum of token counts remains constant. This constraint is crucial when dealing with discrete data, like codebook indices, where the total number of tokens represents a fixed budget. Standard diffusion models or autoregressive models may not inherently enforce this constraint, leading to instability or suboptimal results. The ‘Fixed-Sum’ approach probably involves a novel training or inference strategy that explicitly incorporates this constraint, perhaps through a modified loss function or a projection step. This could lead to more stable training and improved generation quality, as the model is guided to explore solutions that adhere to the fixed-sum prior. Enforcing the Fixed-Sum Constraint is Crucial. Benefits include more stable training and better results

Dual Transform
#

The dual transformation mechanism is a pivotal component, addressing the challenge of modeling set-structured data. Traditional sequential models struggle with permutation invariance, a key characteristic of sets. This transformation cleverly converts the unordered set into a structured sequence while preserving critical information. By counting the occurrences of each unique token index, the method creates a fixed-length vector (count vector) where each element represents the frequency of a particular codebook item. The transformation ensures a bijective mapping, maintaining all original data while enabling the use of sequential modeling techniques. The resulting sequence possesses three crucial structural priors: a fixed length (equal to the codebook size), discrete count values representing token frequencies, and a fixed-sum constraint, where the total count equals the number of tokens. These priors effectively guide the subsequent modeling process, transforming a complex set modeling problem into a more tractable sequence modeling task.

Robust Semantics
#

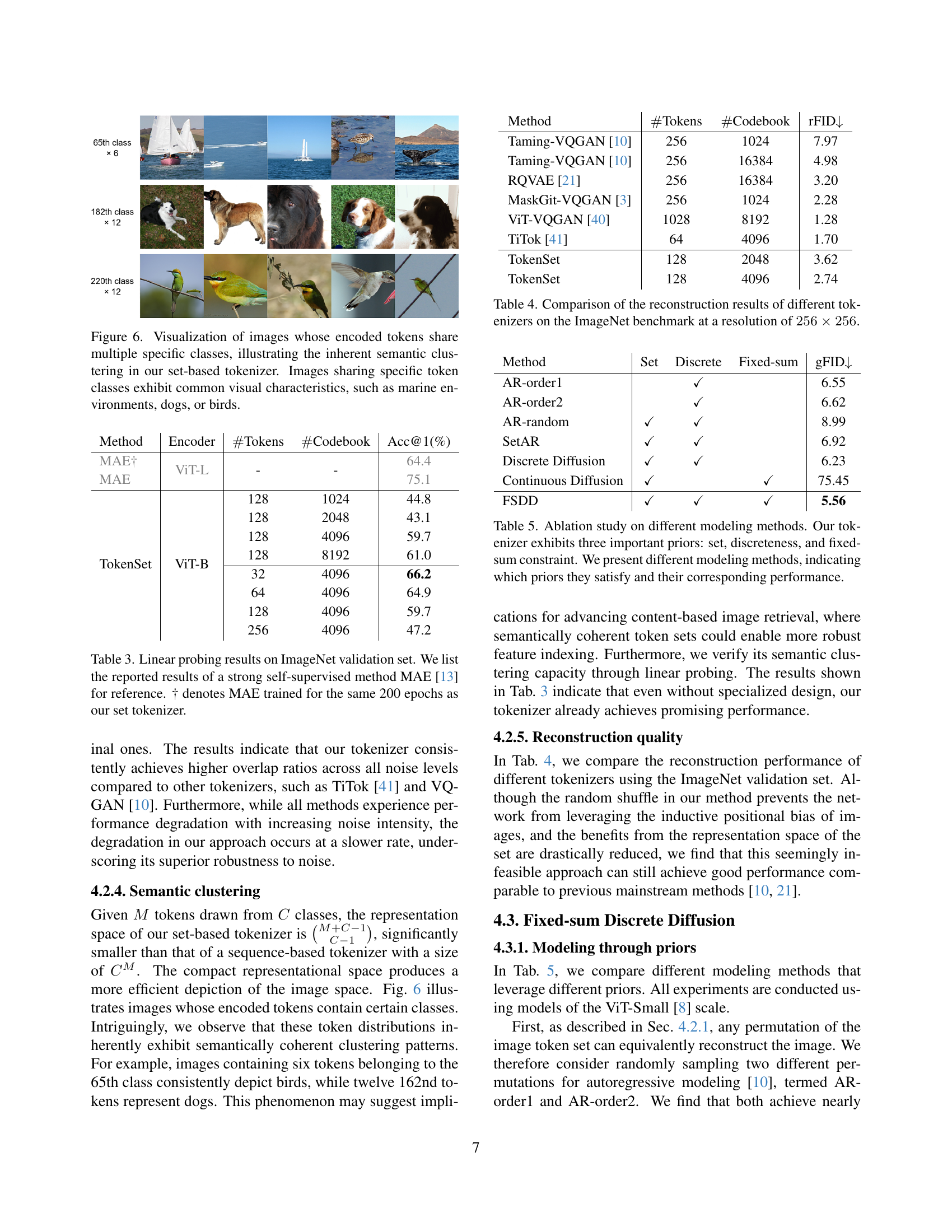
The concept of “Robust Semantics” in the context of image processing and generation, as it relates to the paper’s focus, is intriguing. It likely refers to the ability of the system to maintain a consistent and meaningful representation of an image’s content even when faced with variations or perturbations. This could encompass resilience to noise, occlusions, changes in lighting, or even slight alterations in object pose or appearance. A system with robust semantics would not only be able to recognize the objects and scenes depicted but also understand their relationships and context in a way that is stable and reliable. Achieving this requires a representation that is less sensitive to pixel-level variations and more attuned to the underlying semantic structure of the image. In essence, the system should focus on the ‘what’ and ‘how’ of the image content rather than the specific ‘where’ of each pixel. The paper aims to accomplish robust semantics using a novel technique. TokenSet dynamically allocate capacity based on semantics complexity to give superior robustness to local perturbations.

Beyond Sequences
#

The research paper introduces a paradigm shift, moving away from traditional sequence-based image processing. TokenSet introduces an unordered set of tokens dynamically allocating coding capacity, which deviates significantly from conventional methods that rely on fixed-position latent codes and uniform compression ratios. By representing images as sets, the model achieves enhanced global context aggregation and greater robustness to local perturbations. This set-based tokenization, along with fixed-sum discrete diffusion, facilitates semantic-aware representation and generation quality. The key innovation lies in transforming the complex problem of modeling unordered data into a manageable sequence modeling task through a dual transformation mechanism. The framework’s ability to simultaneously handle discrete values, fixed sequence length, and summation invariance enables more effective set distribution modeling, surpassing the limitations of existing sequence-based approaches and paving the way for new generative model architectures.

More visual insights
#

More on figures

🔼 The figure illustrates the process of converting an image into an unordered set of tokens. The input image is processed by an encoder, which combines image patches and learnable latent tokens. The encoder outputs continuous representations which are then discretized using a VQ-VAE codebook. This results in a 1D sequence of tokens which then has the positional information removed by randomly shuffling the order of the tokens before feeding to the decoder. The decoder reconstructs the image from the unordered set of tokens, demonstrating the method’s permutation invariance.
read the caption
Figure 2: Pipeline of our set tokenizer.

🔼 This figure illustrates the Fixed-Sum Discrete Diffusion process, a key component of the proposed image generation method. It shows how a sample from a noisy distribution (at noise level t=0.6) is generated by combining the initial clean image distribution and a fully noisy distribution. The process also incorporates a greedy adjustment step to enforce the fixed-sum constraint, ensuring the summation of all elements in the sample remains constant. This constraint is crucial for maintaining the bijection between sets and sequences. Samples that were removed during the adjustment phase to satisfy this constraint are marked with dashed lines. The process visually demonstrates how the algorithm iteratively approaches a clean image representation whilst adhering to the defined constraint.
read the caption
Figure 3: Fixed-Sum Diffusion Process. Sample Xtsubscript𝑋𝑡X_{t}italic_X start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT at noise level t=0.6𝑡0.6t=0.6italic_t = 0.6 is first sampled from the mixed gaussian distribution of X0subscript𝑋0X_{0}italic_X start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT and X1subscript𝑋1X_{1}italic_X start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT, and then adjusted through greedy adjustment. Samples dropped during greedy adjustment are marked with dashed line.

🔼 This figure demonstrates the permutation invariance of the proposed set-based tokenizer. It shows the reconstruction of an image from its encoded tokens arranged in different orders: (a) the original image; (b) tokens in the original order; (c) tokens in reversed order; (d) randomly shuffled tokens; (e) tokens sorted in ascending order; (f) tokens sorted in descending order. The visual similarity between all six reconstructed images confirms the permutation invariance—the reconstruction is insensitive to token ordering.
read the caption
(a) Original image

🔼 This image shows the reconstruction of an image from its encoded tokens in their original order. This is part of an experiment to demonstrate the permutation invariance of the proposed set-based tokenization method. The image quality should be identical to reconstructions from other token orderings (reversed, shuffled, sorted ascending, sorted descending), highlighting that the method is not sensitive to the sequence of tokens.
read the caption
(b) Original order

🔼 This image shows a reconstruction of an image from its encoded tokens, where the order of the tokens has been reversed. This demonstrates the permutation invariance of the image set tokenizer. The visual appearance is identical to the original image, highlighting that the reconstruction is not sensitive to the ordering of the tokens.
read the caption
(c) Reversed order

🔼 This image shows the reconstruction of an image from its encoded tokens, but with the order of those tokens randomly shuffled. Despite the random order, the reconstructed image remains identical to the reconstructions from other token orders (original, reversed, ascending, descending), visually demonstrating the permutation invariance achieved by the set-based tokenization method. This property means the model’s performance is unaffected by the order of the input tokens, a key advantage of the set-based approach.
read the caption
(d) Random shuffle

🔼 This image shows the reconstruction of an image from its encoded tokens, which are sorted in ascending order. This demonstrates the permutation invariance of the set-based tokenizer. Even though the order of tokens has been changed, the reconstructed image remains the same as the original. This highlights the model’s ability to reconstruct images regardless of the order of encoded tokens, proving the effectiveness of representing images as an unordered set of tokens rather than a sequence.
read the caption
(e) Sorted ascending

🔼 This figure shows the reconstruction results of an image using tokens in a sorted descending order. This demonstrates that the set-based tokenizer in the proposed method is permutation-invariant. The identical results in this image compared to the other images (a-e) in the figure highlight that changing the token order during decoding does not impact the final image reconstruction. The images are identical because the model learns to treat tokens as a set, ignoring their position.
read the caption
(f) Sorted descending

🔼 This figure shows six reconstructed images from the same encoded tokens, but with different ordering. The first image uses the original order of tokens, followed by the reversed order, a random shuffle, and then ascending and descending sorted orders. Despite the different arrangements of input tokens, all six resulting images are identical. This demonstrates the permutation invariance of the set-based image tokenizer, proving that the order of tokens does not affect the final reconstructed image.
read the caption
Figure 4: Visual comparison of the reconstructed images from various order permutations of the encoded tokens. All reconstructed images are identical, demonstrating the set-based tokenizer is permutation-invariance.

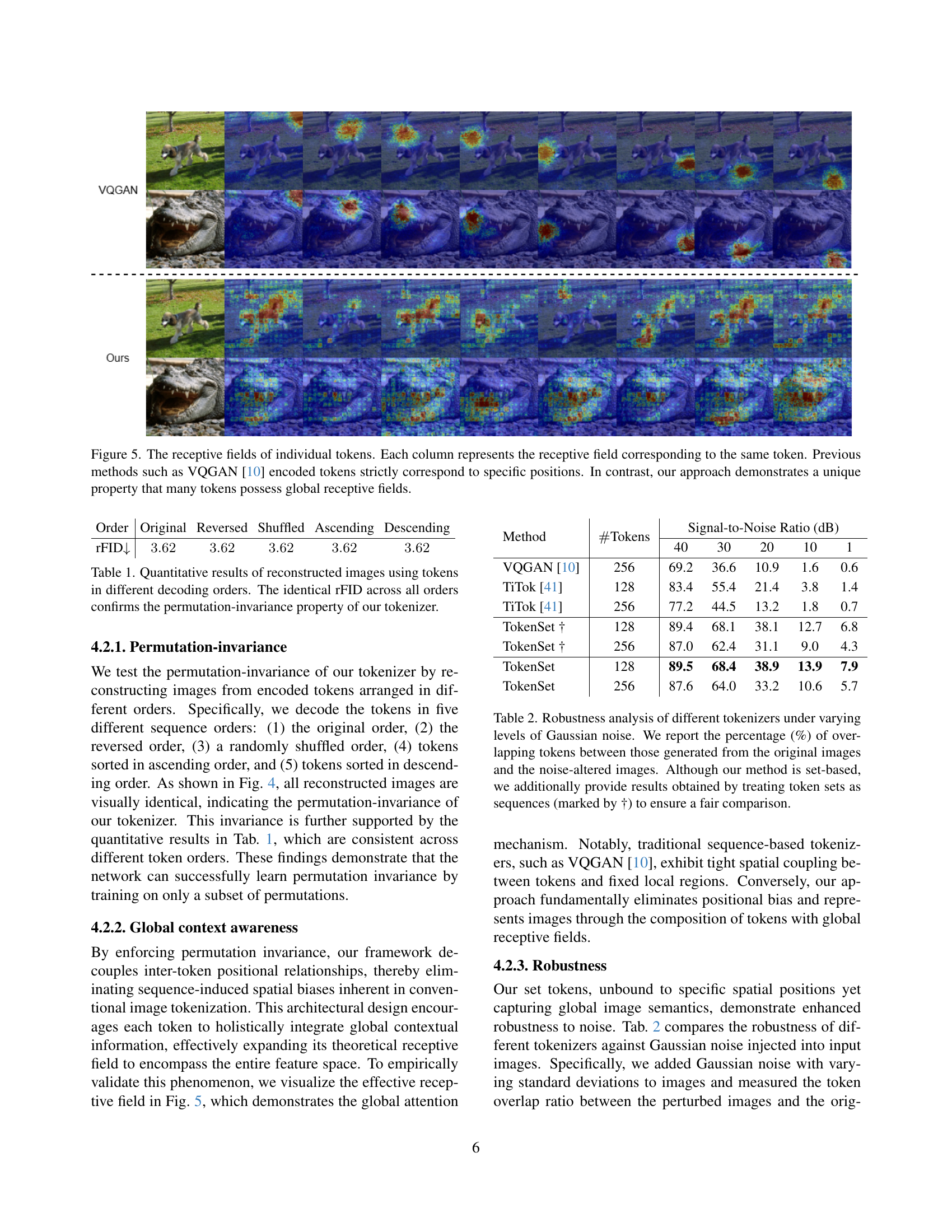
🔼 Figure 5 visualizes the receptive fields of individual tokens generated by the proposed method and compares them to those of previous methods like VQGAN. Each column displays the receptive field for the same token. Previous methods, such as VQGAN, show tokens that strictly correspond to specific spatial image locations. In contrast, the proposed method shows that many tokens have receptive fields that span across a significant portion of the image, demonstrating a global contextual awareness.
read the caption
Figure 5: The receptive fields of individual tokens. Each column represents the receptive field corresponding to the same token. Previous methods such as VQGAN [10] encoded tokens strictly correspond to specific positions. In contrast, our approach demonstrates a unique property that many tokens possess global receptive fields.

More on tables

Method	$\#$ Tokens	Signal-to-Noise Ratio (dB)
Method	$\#$ Tokens	40	30	20	10	1
VQGAN [10]	256	69.2	36.6	10.9	1.6	0.6
TiTok [41]	128	83.4	55.4	21.4	3.8	1.4
TiTok [41]	256	77.2	44.5	13.2	1.8	0.7
TokenSet †	128	89.4	68.1	38.1	12.7	6.8
TokenSet †	256	87.0	62.4	31.1	9.0	4.3
TokenSet	128	89.5	68.4	38.9	13.9	7.9
TokenSet	256	87.6	64.0	33.2	10.6	5.7

🔼 This table presents a robustness analysis comparing various image tokenization methods under different levels of Gaussian noise. The results show the percentage of overlapping tokens between the tokens generated from original images and those generated from noisy versions of the same images. This overlapping token percentage is used as a metric to quantify the robustness of the methods against noise. The table includes results for both set-based and sequence-based tokenization methods, allowing for a fair comparison.
read the caption
Table 2: Robustness analysis of different tokenizers under varying levels of Gaussian noise. We report the percentage (%) of overlapping tokens between those generated from the original images and the noise-altered images. Although our method is set-based, we additionally provide results obtained by treating token sets as sequences (marked by †) to ensure a fair comparison.

Method	Encoder	$\#$ Tokens	$\#$ Codebook	Acc@1(%)
MAE†	ViT-L	-	-	64.4
MAE	ViT-L	-	-	75.1
TokenSet	ViT-B	128	1024	44.8
		128	2048	43.1
		128	4096	59.7
		128	8192	61.0
		32	4096	66.2
		64	4096	64.9
		128	4096	59.7
		256	4096	47.2

🔼 This table presents the results of linear probing experiments conducted on the ImageNet validation set. Linear probing assesses the quality of learned representations by evaluating the performance of a linear classifier trained on top of them. The table compares the top-1 accuracy achieved by different methods on this benchmark task. Specifically, it shows the performance of the proposed ‘TokenSet’ approach with varying configurations (using different vision transformer backbones and codebook sizes), and includes a comparison to a strong self-supervised learning baseline, MAE [13]. The ‘†’ symbol indicates that the MAE model was trained for the same number of epochs (200) as the proposed method’s encoder for a fair comparison.
read the caption
Table 3: Linear probing results on ImageNet validation set. We list the reported results of a strong self-supervised method MAE [13] for reference. † denotes MAE trained for the same 200 epochs as our set tokenizer.

Method	$\#$ Tokens	$\#$ Codebook	rFID $\downarrow$
Taming-VQGAN [10]	256	1024	7.97
Taming-VQGAN [10]	256	16384	4.98
RQVAE [21]	256	16384	3.20
MaskGit-VQGAN [3]	256	1024	2.28
ViT-VQGAN [40]	1028	8192	1.28
TiTok [41]	64	4096	1.70
TokenSet	128	2048	3.62
TokenSet	128	4096	2.74

🔼 This table compares the performance of different image tokenization methods on the ImageNet dataset. The comparison is based on the Fréchet Inception Distance (FID) score, a metric that evaluates the quality of generated images by comparing them to real images. Lower FID scores indicate better reconstruction quality. The table shows the FID scores achieved by several methods, including VQGAN, RQVAE, MaskGIT-VQGAN, VIT-VQGAN, TiTok, and the proposed TokenSet method. The results are presented for different configurations in terms of the number of tokens and the size of the codebook used.
read the caption
Table 4: Comparison of the reconstruction results of different tokenizers on the ImageNet benchmark at a resolution of 256×256256256256\times 256256 × 256.

Method	Set	Discrete	Fixed-sum	gFID $\downarrow$
AR-order1		✓		6.55
AR-order2		✓		6.62
AR-random	✓	✓		8.99
SetAR	✓	✓		6.92
Discrete Diffusion	✓	✓		6.23
Continuous Diffusion	✓		✓	75.45
FSDD	✓	✓	✓	5.56

🔼 This table presents an ablation study comparing different image generation modeling methods. The key is to analyze how the performance changes when incorporating three crucial properties from the proposed TokenSet method: set-based representation (unordered sets), discrete value representation (integer counts), and fixed-summation constraint (sum of counts equals total tokens). Each method is evaluated on its ability to satisfy these constraints and its resulting performance (measured by the gFID metric). This allows for assessing the individual and combined contributions of these properties to the overall model effectiveness.
read the caption
Table 5: Ablation study on different modeling methods. Our tokenizer exhibits three important priors: set, discreteness, and fixed-sum constraint. We present different modeling methods, indicating which priors they satisfy and their corresponding performance.

$\#$ Tokens	$\#$ Codebook	rFID $\downarrow$	gFID $\downarrow$
128	1024	6.51	9.93
128	2048	3.62	7.12
128	4096	2.74	5.56
128	8192	2.35	8.76
32	4096	5.54	6.91
64	4096	3.54	6.03
128	4096	2.74	5.56
256	4096	2.60	7.07
512	4096	2.88	9.37

🔼 This table presents the results of an ablation study investigating the impact of varying the number of tokens and codebook sizes on both the reconstruction and generation performance of the proposed model. It shows how FID and gFID scores change as these hyperparameters are adjusted, providing insights into the optimal configuration for balancing reconstruction quality and generative capacity.
read the caption
Table 6: Impact of token numbers and codebook sizes on reconstruction and generation performance.

Method	$\#$ Tokens	$\#$ Codebook	$\#$ Params	gFID $\downarrow$
VQGAN [10]	256	1024	1.4B	15.78
VQ-Diffusion [12]	1024	2886	370M	11.89
MaskGiT [3]	256	1024	227M	6.18
LlamaGen [36]	256	16384	111M	5.46
LlamaGen [36]	256	16384	3.1B	2.18
TiTok [41]	128	4096	287M	1.97
TokenSet-S	128	4096	36M	5.56
TokenSet-B	128	4096	137M	5.09

🔼 This table presents a comparison of the performance of various image generation models on the ImageNet dataset. The models are evaluated at a resolution of 256x256 pixels using the FID and KID metrics, which assess the quality of generated images. The table allows for a quantitative comparison of different approaches in terms of their image generation capabilities.
read the caption
Table 7: Modeling performance comparison on the ImageNet benchmark at 256×256256256256\times 256256 × 256 resolution.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Set-based Tokens#

Fixed-Sum Models#

Dual Transform#

Robust Semantics#

Beyond Sequences#

More visual insights#

Full paper#