TL;DR#
Self-supervised learning (SSL) in 3D point clouds lags behind image SSL, hindering applications in autonomous driving and robotics. Existing methods often rely on easily accessible geometric cues, leading to a “geometric shortcut” that prevents learning robust representations. This results in poor performance when evaluated with linear probing, a standard measure of representation quality. Current SSL models collapse to low-level spatial features. This is due to the 3D point cloud operators and easily accessible normal direction or point height.
This paper introduces a new SSL framework that addresses the geometric shortcut by obscuring spatial information and emphasizing input features. The approach involves applying SSL losses at coarser spatial scales, using a point self-distillation framework, and employing scaling techniques. The resulting model demonstrates strong zero-shot capabilities and achieves exceptional parameter and data efficiency. It significantly improves linear probing accuracy and achieves SOTA results across various 3D perception tasks. They trained on 140k point clouds through self-distillation.
Key Takeaways#
Why does it matter?#
This paper introduces a reliable self-supervised learning method for 3D point clouds, enhancing representation quality and data efficiency. It significantly boosts performance in various 3D perception tasks, opening avenues for more robust and generalizable 3D models and cross-modal learning.
Visual Insights#

🔼 Sonata, a self-supervised learning method for reliable 3D point cloud representations, is presented. Figure 1 highlights Sonata’s key advantages: superior performance on various 3D perception tasks; high efficiency in linear probing, requiring minimal additional parameters for strong performance; a decoder-free architecture that allows for more flexible and scalable models; the ability to reveal semantic structure in its representations; and robust spatial reasoning capabilities, even with significant data augmentation. The figure visually demonstrates these properties with visualizations and performance metrics.
read the caption
Figure 1: Main properties. Sonata leads to reliable 3D self-supervised pretraining with the following superior and emerging properties: 1. Perception. Sonata advances state-of-the-art results across 3D indoor and outdoor perception tasks; 2. Linear probing. With less than 0.2% learnable parameters, Sonata achieves strong and usable linear probing performance which is 3.3×\times× better than previous SOTA; 3. Decoder-free. Sonata moves beyond the inflexible U-Net structure, offering multi-scale representations that unchain future 3D research from previous architectural constraints. 4. Semantic awareness. Sonata reveals semantic structure in PCA and K-means visualizations. 5. Spatial reasoning. Sonata allows spatial correspondence even under strong augmentations as visualized via feature similarity.
In-depth insights#
Geometric Shortcut#
The “Geometric Shortcut” refers to models collapsing to low-level spatial cues like normal direction or point height instead of learning deeper semantics. This is unique to 3D point cloud SSL because spatial information is easily accessible through point coordinates, unlike images where it’s embedded in features. Models exploit this shortcut, hindering their ability to learn robust representations. To counteract the Geometric Shortcut, the paper obfuscates spatial information. It is done by applying SSL losses at coarser spatial scales to minimize information of the masked point. Input features are emphasized to steer model from spatial biases.
Decoder-Free SSL#
Decoder-free self-supervised learning (SSL) marks a significant departure from traditional architectures, primarily addressing limitations associated with U-Net structures in 3D point cloud processing. The inflexible U-Net architecture, with its tight encoder-decoder coupling via skip connections, often restricts generalization and flexibility. By eliminating the decoder, the model can focus on learning more robust and transferable representations within the encoder. This approach also allows for multi-scale representations, unchaining 3D research from architectural constraints and facilitating the exploration of diverse task heads. This decoder removal has several benefits which are: increases feature channels participating in self-distillation, streamlines the pipeline by reducing points in the pretext task, and obscuring geometric cues. Focusing solely on the encoder reduces reliance on low-level spatial information, mitigating the geometric shortcut and enabling the learning of richer semantic features. This paradigm shift supports the development of SSL models with improved linear probing performance and broader applicability across various 3D tasks.
Self-Distillation#
Self-distillation emerges as a pivotal technique, transferring knowledge from a cumbersome teacher network to a streamlined student model. The teacher, often an exponential moving average of the student, guides the student by providing soft targets. These soft targets, probability distributions over classes, carry richer information than hard labels, enabling the student to better generalize. Self-distillation can also be used to refine the student model with global information in local view, by aligning representations through the distillation of embeddings, reducing reliance on geometric information, and improving performance. A well-designed self-distillation framework balances knowledge transfer and exploration, crucial for robust learning.
Robust Training#
While ‘Robust Training’ isn’t explicitly mentioned, the paper implicitly addresses it through techniques designed to prevent the model from exploiting ‘geometric shortcuts’. The core idea revolves around making the learning process more challenging and forcing the model to rely less on easily accessible, low-level spatial features (like point height or normal directions). The progressive parameter scheduler plays a key role here, gradually increasing the difficulty of pretext tasks (masking ratios, mask sizes) to prevent early convergence to trivial solutions. This is analogous to curriculum learning, where the model is progressively exposed to harder examples, preventing it from getting ‘stuck’ in local minima or overfitting to simple cues. Furthermore, the masking strategy (applying stronger jitter to masked points) is intended to disrupt spatial relationships, making it harder for the model to rely solely on point coordinates. These efforts contribute to more robust representations, less sensitive to noise or variations in input geometry, and better generalization across different datasets and tasks. This ultimately enhances the reliability and usability of the learned representations in downstream applications.
Cross-Modal SSL#
Cross-modal self-supervised learning (SSL) holds significant promise for leveraging information across different data modalities, such as images, point clouds, text, and audio. The core idea is to train a model to understand the relationships between these modalities without explicit human labels. For example, a model could be trained to associate images with corresponding text descriptions, or to predict the sound that corresponds to a particular video frame. The benefits of cross-modal SSL are numerous. First, it can improve the performance of models on tasks where only one modality is available, by leveraging information from other modalities during training. Second, it can enable new applications that require understanding the relationships between modalities, such as cross-modal retrieval and generation. Despite its potential, cross-modal SSL also faces several challenges. These include how to effectively fuse information from different modalities, how to handle missing or noisy data, and how to scale up to large datasets. Overcoming these challenges will be crucial for realizing the full potential of cross-modal SSL.
More visual insights#
More on figures

🔼 This figure demonstrates the concept of ‘geometric shortcuts’ in 3D self-supervised learning. It visualizes pairwise similarity heatmaps for three different models (CSC, MSC, and Sonata) when computing similarities between a point on a sofa arm and all other points in the scene. CSC’s heatmap shows similarities largely aligned with surface normals, indicating that the model focuses on low-level geometric cues. MSC’s heatmap displays high similarity with points sharing similar heights, revealing an over-reliance on point height information. In contrast, Sonata’s heatmap exhibits strong similarities among all points belonging to the sofa arms, demonstrating that it has learned higher-level semantic concepts and spatial relationships rather than simply relying on surface normals or point heights.
read the caption
Figure 2: Geometric shortcut. We select a point on the sofa arm and compute pairwise similarity with other points. The similarity heatmap reveals that CSC [38] collapses to surface normals, and MSC [88] overfits to point height. In contrast, our Sonata can extract higher-level concepts, as can be seen by the high similarity between all sofa arms highlighted in red.
🔼 Figure 3 illustrates the core concept of ‘geometric shortcut’ in 3D self-supervised learning (SSL). It compares 2D image data and 3D point cloud data. When the input features (color information in the images, and potentially semantic features in the point clouds) are removed, images lose essentially all their information. However, 3D point clouds still retain geometric information inherent in the point positions themselves. Because 3D point cloud operators directly use this positional data, models can easily exploit these low-level geometric cues, rather than learning higher-level semantic features. This reliance on readily available geometric information is what the authors refer to as the ‘geometric shortcut’, hindering the effectiveness of 3D SSL.
read the caption
Figure 3: The geometric shortcut is unique to 3D. When comparing the information contained in 2D image and 3D point cloud data after removing the input feature (indicated by color), it is evident that in images all information is within the input feature. Whereas point clouds retain geometric information in point positions, which is directly utilized by operators. This characteristic leads to what we term geometric shortcuts in 3D SSL.
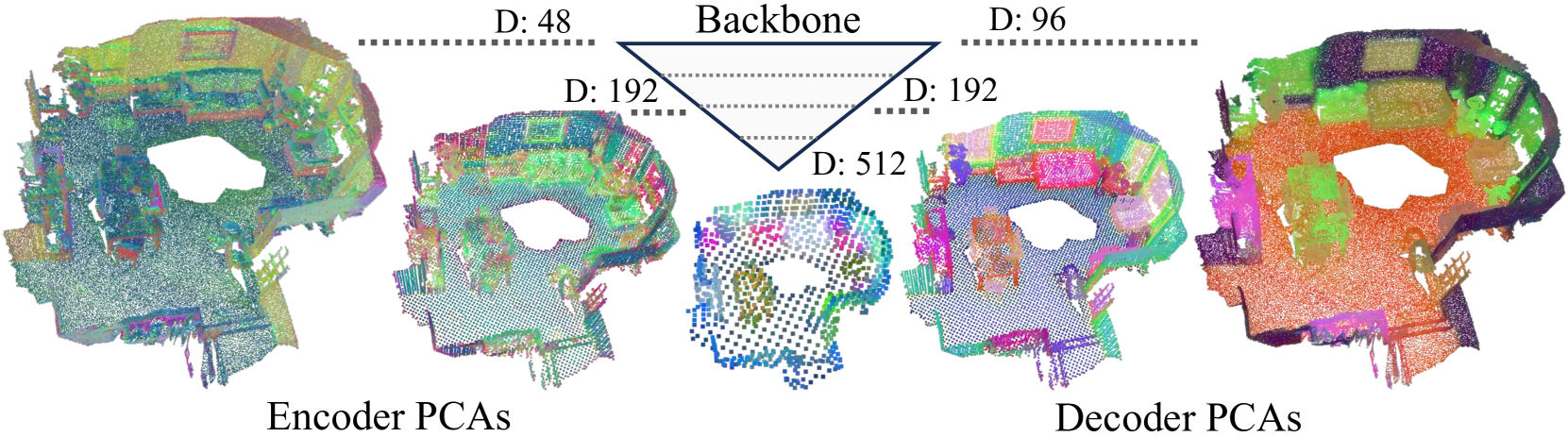
🔼 This figure visualizes PCA embeddings from different layers of a hierarchical encoder-decoder network, trained on semantic segmentation task. The visualization reveals how the encoder learns increasingly global geometric information as the point cloud resolution decreases, while the decoder focuses on generating more structured and uniform representations relevant for specific downstream tasks. This contrast illustrates the distinct roles of the encoder (feature learning) and decoder (task-specific refinement) in a hierarchical architecture, and the different types of information each component extracts from point cloud data. The encoder captures a broad range of features, initially dispersed but becoming more globally structured as the point cloud coarsens. Conversely, the decoder’s outputs are more spatially uniform and task-focused.
read the caption
Figure 4: What is learned by the hierarchical backbone? We visualize PCA embeddings from different stages of a hierarchical encoder and decoder, trained for semantic segmentation. The encoder captures diverse and dispersed feature patterns, indicating a broad range of information. Notably, as the point cloud becomes coarser, accessible geometric information within point coordinates becomes increasingly global. In contrast, the decoder’s representations are more uniform and structured, suggesting a focus on refining features for task-specific outputs.
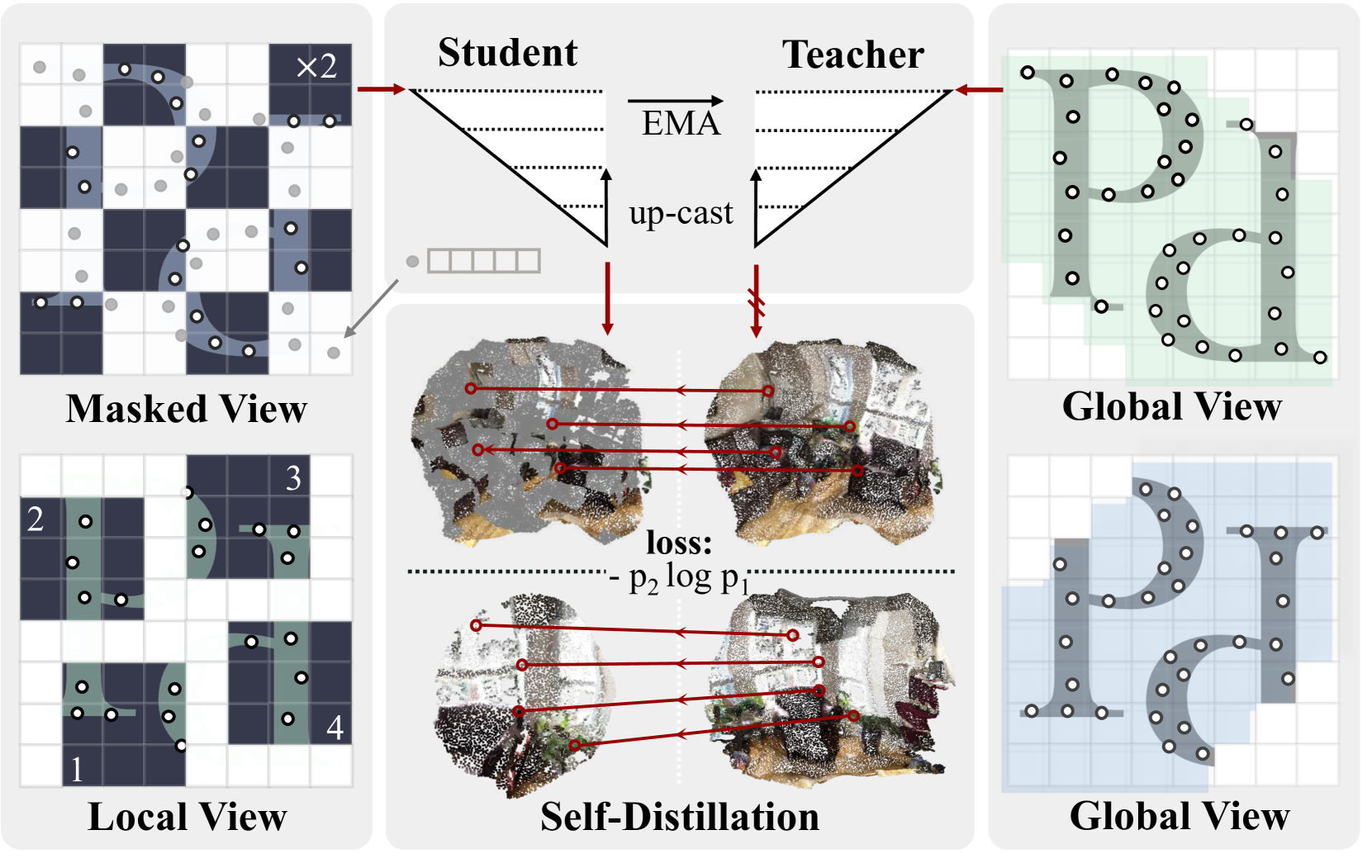
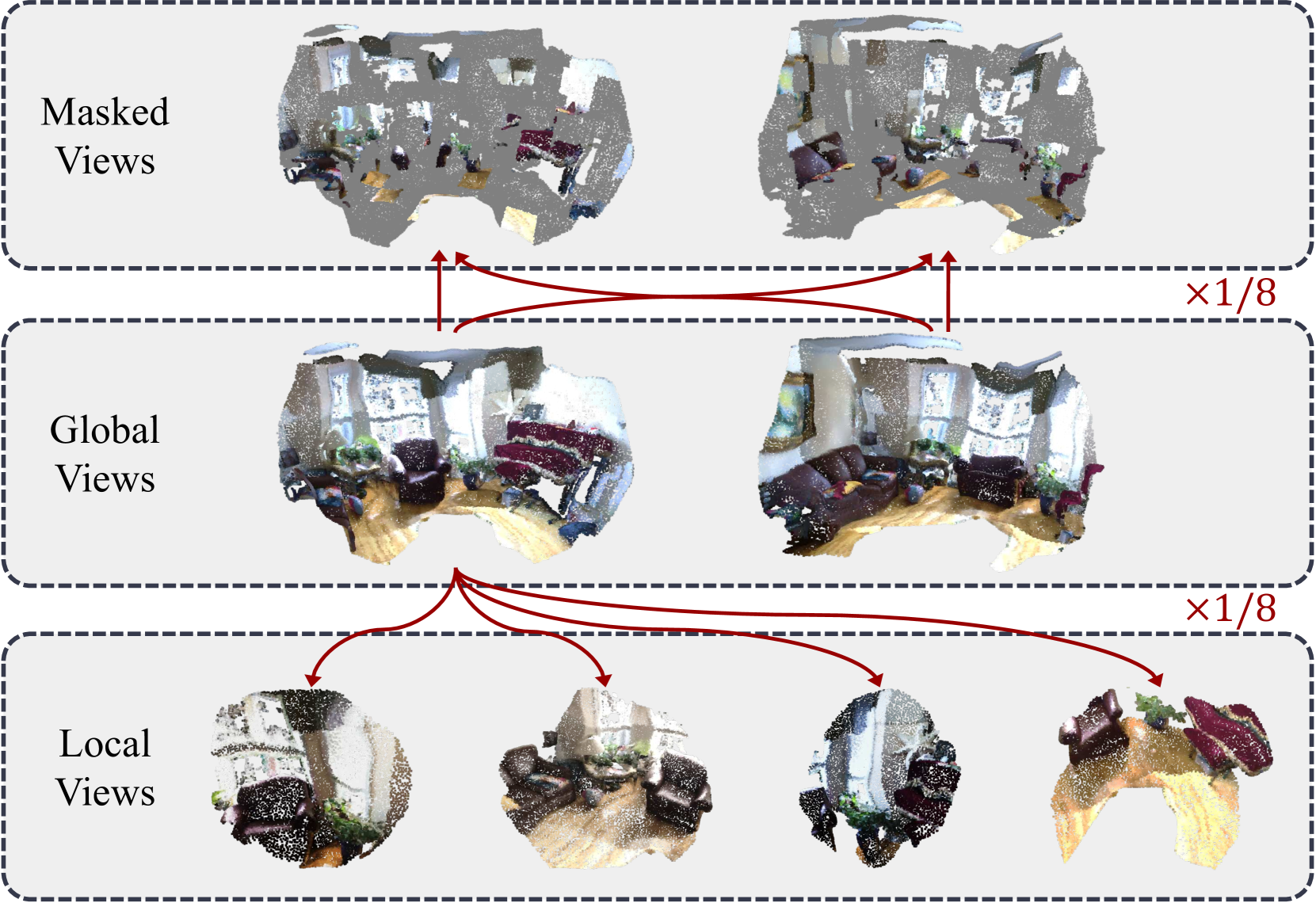
🔼 Sonata’s self-distillation framework uses three types of views: local, global, and masked. Local views are created with small, dedicated spatial and photometric augmentations. Global views use larger augmentations, providing more context. Masked views are generated by randomly removing grid-based patches from the global views. A student network processes the local and masked views, while a teacher network processes the global views. The student learns by matching points in the local and masked views to their corresponding points in the global view (based on their original, un-augmented locations), effectively distilling knowledge from the teacher.
read the caption
Figure 5: Self-distillation framework of Sonata. (1) Local views (bottom left) and global views (right) are generated with dedicated spatial and photometric augmentations, while masked views are created by randomly masking out grid-based patches from the global views (top left). (2) Embeddings from local and masked views are extracted by the student, with global views processed by the teacher (top). (3) Points from local and masked views are matched with corresponding points in the global views based on their original spatial distance, allowing for the distillation of embeddings from global views to local and masked views (bottom).

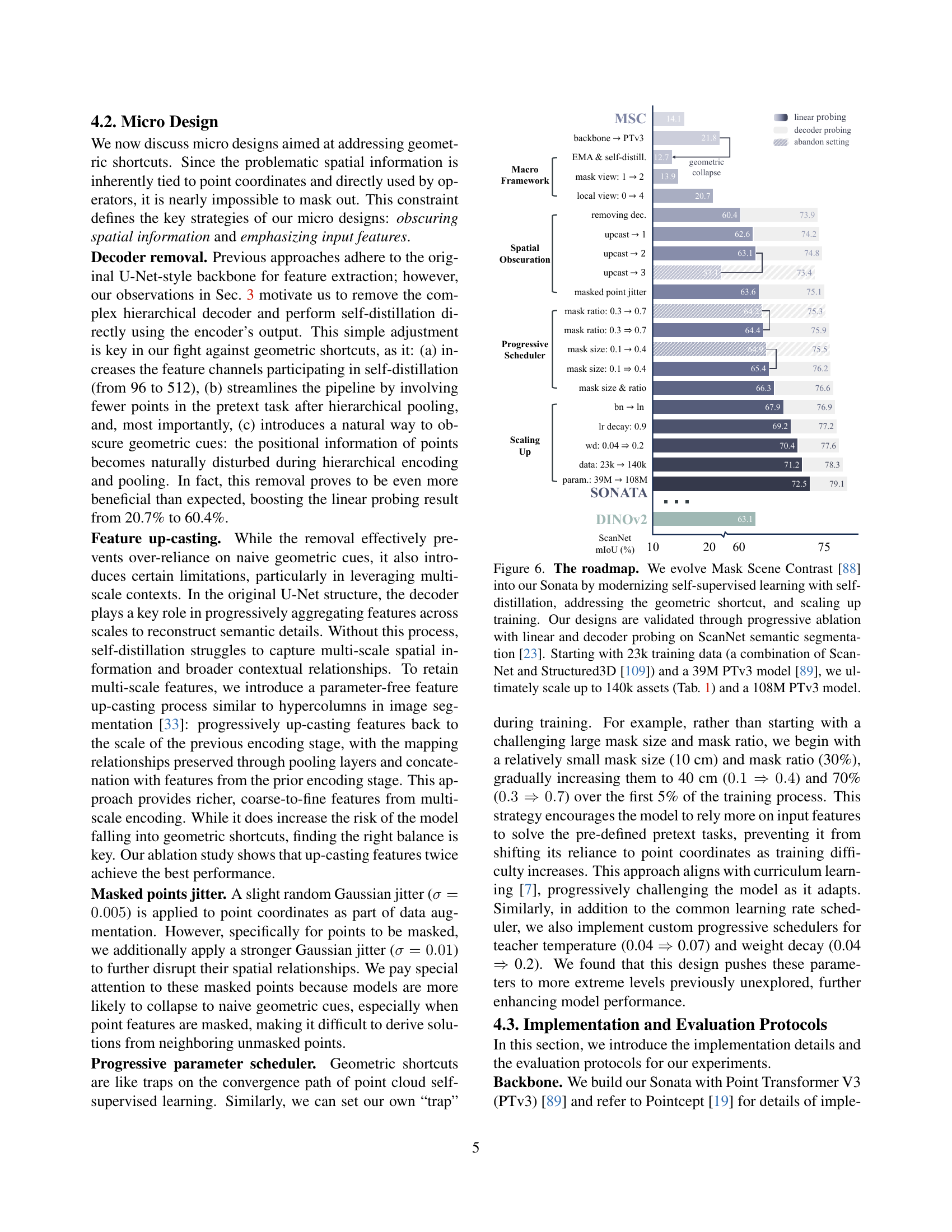
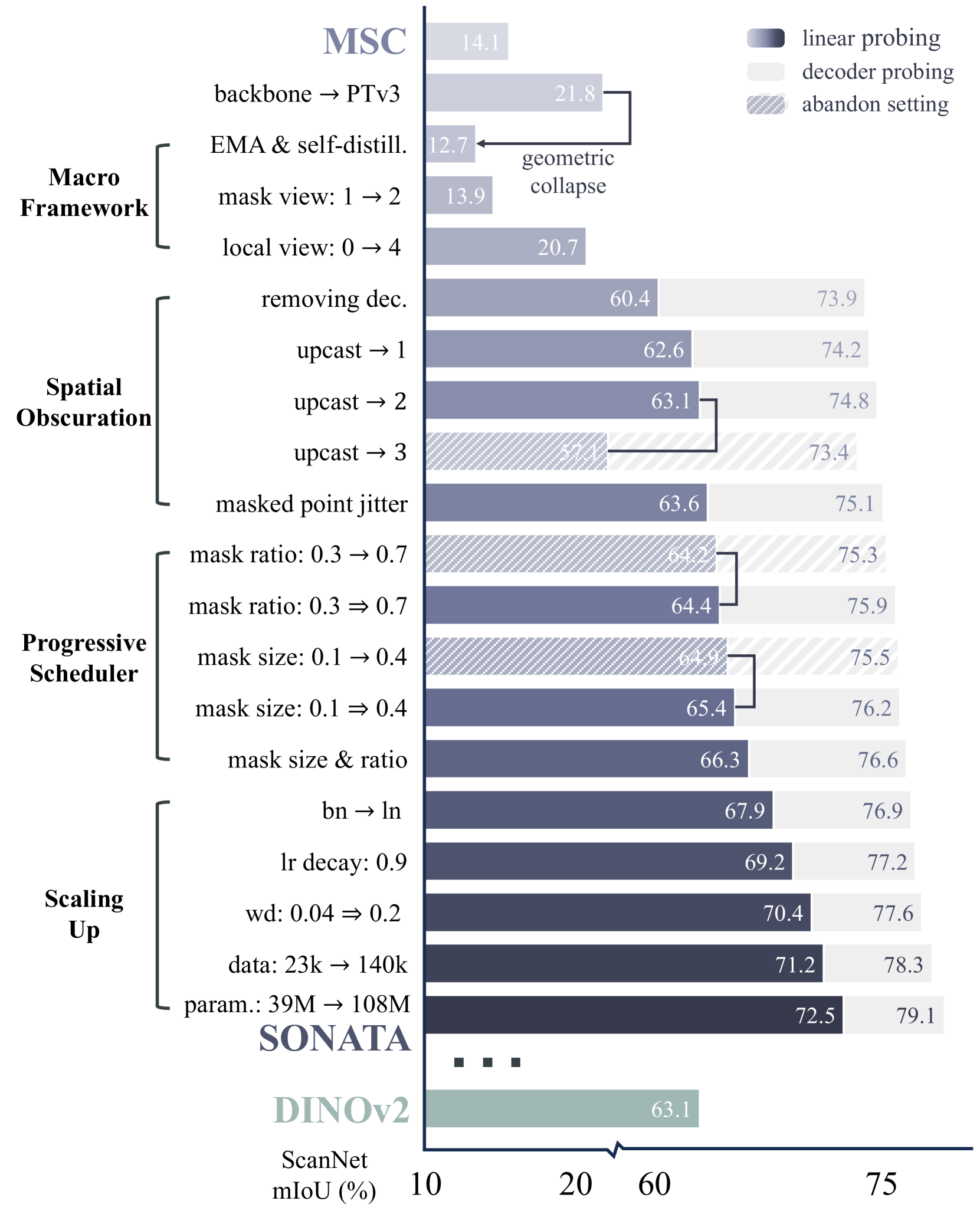
🔼 Figure 6 illustrates the development of the Sonata model from Mask Scene Contrast [88]. It shows a step-by-step improvement process, starting with a smaller dataset and model (23k training samples, 39M parameter PTv3 model), and incrementally adding techniques like self-distillation to address the geometric shortcut problem inherent in 3D point cloud data. The process culminates in a larger-scale model (140k samples, 108M parameter PTv3 model) that achieves superior performance on ScanNet semantic segmentation [23]. Each step in the roadmap includes linear and decoder probing results to validate the effectiveness of the design choices. The figure emphasizes the iterative improvements and scaling-up strategies employed in creating the Sonata model.
read the caption
Figure 6: The roadmap. We evolve Mask Scene Contrast [88] into our Sonata by modernizing self-supervised learning with self-distillation, addressing the geometric shortcut, and scaling up training. Our designs are validated through progressive ablation with linear and decoder probing on ScanNet semantic segmentation [23]. Starting with 23k training data (a combination of ScanNet and Structured3D [109]) and a 39M PTv3 model [89], we ultimately scale up to 140k assets (Tab. 2) and a 108M PTv3 model.
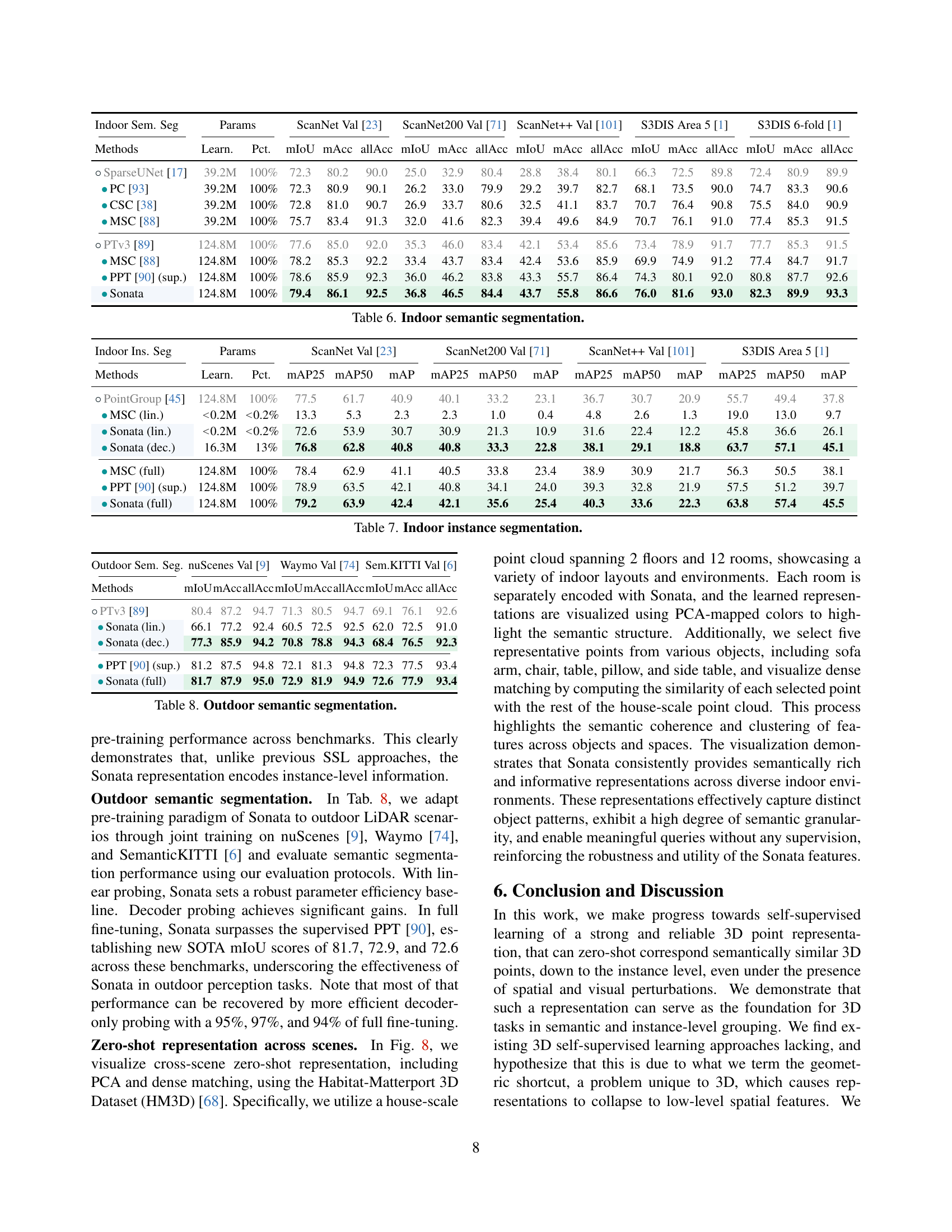
🔼 This table details the datasets used in the Sonata model training. It lists the name of each dataset, whether the data is real or simulated, and the number of training, validation, and test samples. The datasets include indoor and outdoor scenes and are a mix of real and simulated point clouds. The mixed nature of the data helps train a more robust model. The table also shows the total number of samples used in the study.
read the caption
Table 1: Data source collection.

🔼 This table compares the scale of datasets used for training different point cloud self-supervised learning methods. It shows that the Sonata method utilizes a significantly larger dataset (139,768 point clouds) compared to previous methods such as PC (1,613), MSC (6,660), and PPT (23,706). This demonstrates the scale advantage of Sonata’s training data.
read the caption
Table 2: Data scale comparison.
🔼 This figure compares the zero-shot performance of DINOv2 and Sonata, two different self-supervised learning models, on point cloud representation. PCA visualizations are used to highlight the different strengths of each model. DINOv2 excels at capturing fine-grained photometric details (color and texture information), while Sonata is better at distinguishing spatial relationships between points. A combined representation that utilizes both DINOv2 and Sonata features is shown, demonstrating improved coherence and detail compared to either model alone, illustrating their complementary nature and the potential benefits of combining their approaches.
read the caption
Figure 7: Zero-shot comparison with DINOv2. We compare the PCA visualizations of DINOv2, Sonata, and their combined feature representation. DINOv2 excels at capturing photometric details, while Sonata better distinguishes spatial information. The combined model demonstrates improved coherence and detail, showcasing the complementary strengths of both models.

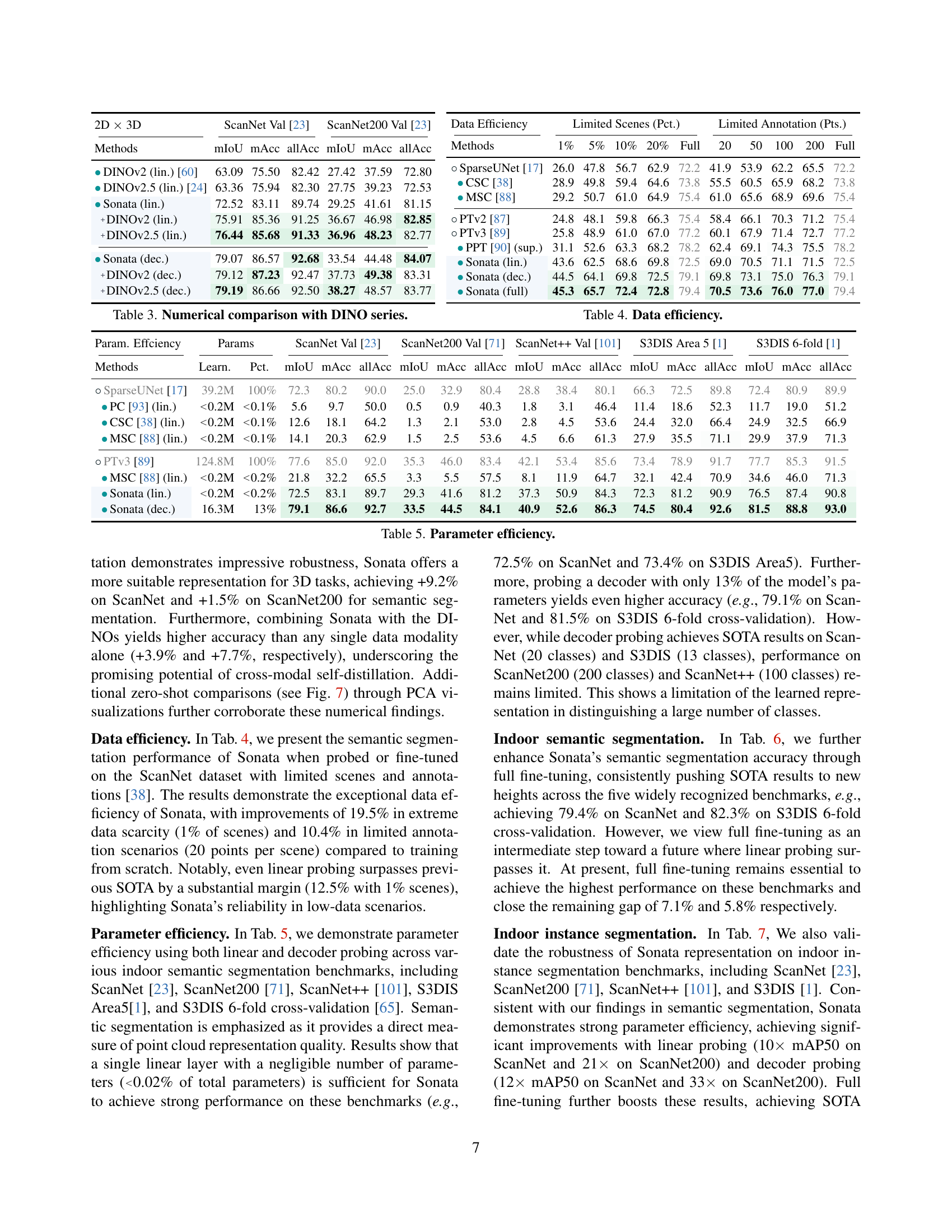
🔼 Table 3 presents a quantitative comparison of the linear and decoder probing results of Sonata against the DINOv2 and DINOv2.5 image-based self-supervised models. The comparison is performed on the ScanNet and ScanNet200 semantic segmentation datasets and includes metrics such as mean Intersection over Union (mIoU), mean accuracy (mAcc), and overall accuracy (allAcc). This table helps demonstrate Sonata’s effectiveness in learning robust 3D representations.
read the caption
Table 3: Numerical comparison with DINO series.
Full paper#