TL;DR#
Generative modeling for biological sequences, like proteins and DNA, faces challenges due to the non-differentiability of categorical variables, resulting in issues such as compounding errors and limited global coherence. Existing methods struggle with scaling to higher dimensions and lack effective controllability during inference. To solve this, the paper tackles these limitations by introducing a framework that improves sequence generation in discrete spaces.
The paper introduces Gumbel-Softmax Flow Matching, which defines a novel Gumbel-Softmax interpolant with a time-dependent temperature parameter. This allows for high-quality, diverse generation and efficient scaling. Additionally, Straight-Through Guided Flows enables training-free guidance, steering the velocity field toward optimal sequence vertices. The framework is shown to be effective in DNA promoter design, protein generation, and target-binding peptide design.
Key Takeaways#
Why does it matter?#
This paper introduces a novel approach for controllable sequence generation that tackles the challenge of scaling to high-dimensional simplices and offers a training-free guidance method. It enables high-quality, diverse sequence generation, providing a robust framework for various biological sequence design tasks. This research is vital for advancing de novo sequence design and personalized medicine.
Visual Insights#

🔼 This figure illustrates the Gumbel-Softmax Flow Matching method. It begins with clean, one-hot encoded biological sequences. A time-dependent temperature parameter is introduced, gradually decreasing the temperature over time. At each time point, a Gumbel-softmax transformation is applied to the clean sequences, creating a noisy distribution of probabilities. This noisy distribution is then inputted to either a parameterized flow model or a score model. These models output a conditional flow velocity or score function, respectively, which guide the generation process toward the target (clean) sequences. The entire process results in a transformation from a noisy distribution to a clean distribution concentrated at the desired sequence.
read the caption
Figure 1: Overview of Gumbel-Softmax Flow Matching. Gumbel-softmax transformations are applied to clean one-hot sequences for varying temperatures dependent on time. The embedded noisy distributions are passed into a parameterized flow or score model and error prediction model to predict the conditional flow velocity and score function.
| Model | MSE () |
|---|---|
| Bit Diffusion (Bit Encoding)* | 0.041 |
| Bit Diffusion (One-Hot Encoding)* | 0.040 |
| D3PM-Uniform* | 0.038 |
| DDSM* | 0.033 |
| Language Model* | 0.033 |
| Dirichlet Flow Matching | 0.029 |
| Fisher Flow Matching | 0.030 |
| Gumbel-Softmax Flow Matching (Ours) | 0.029 |
🔼 This table presents a comparison of the mean squared error (MSE) for various models in predicting the regulatory signal of generated DNA promoter sequences. The models were evaluated using a validation set, and the MSE was calculated by comparing the predicted signal to the true signal (obtained using a pre-trained Sei model [25]). Lower MSE values indicate better model performance. The results include several different generative models, some of which are from previous work (marked with an asterisk, *). This comparison shows how the Gumbel-Softmax Flow Matching model performs against current state-of-the-art methods for this task.
read the caption
Table 1: Evaluation of promoter DNA generation conditioned on transcription profile. MSE was evaluated across all validation batches between the predicted signal of a conditionally generated sequence and the true sequence. Regulatory signals were predicted with a pre-trained Sei model [25]. Numbers with * are from Stark et al. [4]
In-depth insights#
Gumbel Flows#
The Gumbel-Softmax distribution is the core of “Gumbel Flows”, providing a differentiable relaxation of categorical variables. This is crucial for sequence generation, as it allows gradients to flow through discrete choices. The use of a temperature parameter to control the sharpness of the distribution is also interesting; starting with a high temperature for exploration and annealing it for exploitation. Gumbel flows’ potential to model complex dependencies is valuable, especially in biological sequences. By combining the Gumbel-Softmax with flow-based generative models, it enables a powerful and tractable approach to sequence design.
ST Guidance#
It appears that the paper explores the use of a Straight-Through (ST) estimator for guiding the flow-matching process within a Gumbel-Softmax framework. The key idea is to leverage pre-trained classifiers to steer the generated sequences toward regions of higher quality or desired properties. ST Guidance is designed to use readily available classifiers trained on clean sequences, rather than training noisy classifiers. This is helpful since ST guidance leverages straight-through gradients to guide the flow towards optimal sequences by refining the predicted logits in a temperature dependent manner. The classifier guides the generation towards higher scoring sequences, making the process effective and efficient.
Sequence Design#
Sequence design, a pivotal aspect of computational biology, focuses on creating novel sequences with desired properties. In the context of proteins, this involves generating amino acid sequences that fold into specific 3D structures, enabling tailored functionalities. For DNA/RNA, it aims to engineer sequences with targeted regulatory effects or binding affinities. The challenge lies in navigating the vast sequence space efficiently. Computational methods like generative models (GANs, VAEs) and reinforcement learning play a crucial role in this domain, allowing researchers to explore and optimize sequences with higher chances of success compared to random screening. Sequence design holds immense potential for drug discovery, synthetic biology, and materials science. The ability to precisely control biological functions at the sequence level is paramount for advancing these fields.
Protein Generation#
From the context of the paper, the concept of ‘Protein Generation’ seems to revolve around using generative models to design novel protein sequences. The authors likely explore different methods, including flow matching and diffusion models, to overcome the challenges of generating structured sequences in the discrete amino acid space. A key focus is likely on improving the quality, diversity, and structural feasibility of the generated proteins. Another aim is to design proteins with specific functions or binding affinities, such as peptide binders for therapeutic targets. The research explores both unconditional protein generation and conditional protein generation, where the generation process is guided by specific constraints or objectives. The goal is to create tools that can aid in the design of new proteins with desired properties.
Peptide Binders#
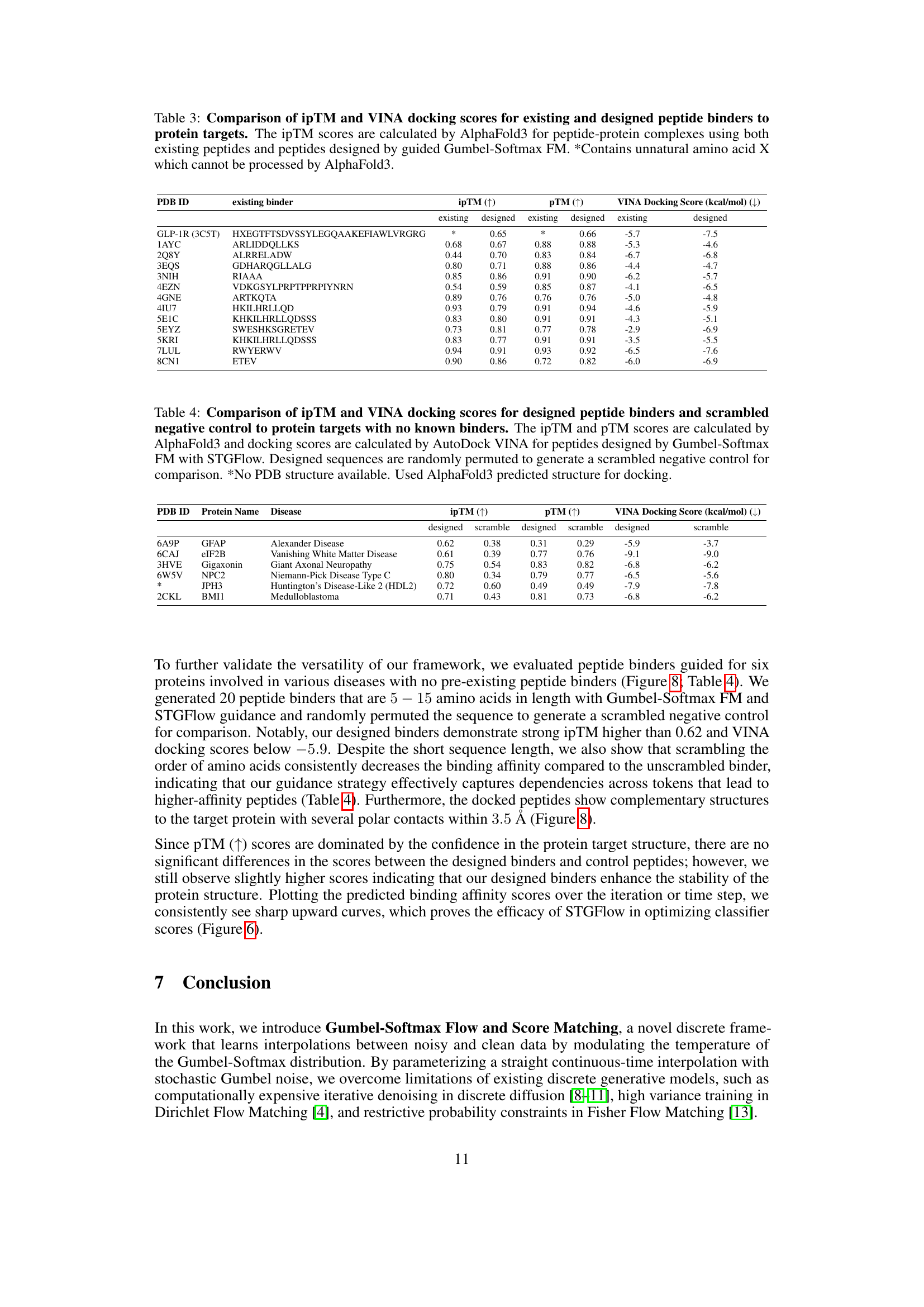
Peptide binder design is a crucial area, particularly for rare diseases. The paper integrates guidance into Gumbel-Softmax FM to create de novo peptides with high target affinity. By generating peptides with similar or higher binding affinity to known binders, it addresses the need for novel therapeutics. The use of the STGFlow algorithm facilitates guided flow paths, enhancing binding potential. The models predict Ka/Ki/IC50 scores, crucial for assessing binding. Comparing designed peptides with existing ones, and employing metrics such as ipTM and VINA docking, validates the efficacy. The consistent generation of peptides with superior binding affinity marks a key advancement. Further, demonstrating effectiveness in diseases lacking known binders signifies a major stride in therapeutic design.
More visual insights#
More on figures

🔼 This figure illustrates the Straight-Through Guided Flows (STGFlow) method. STGFlow uses a pre-trained classifier to guide the generation process without requiring additional classifier training during the generation process. The process begins by sampling M discrete sequences from an intermediate token distribution, represented as xt. Gradients of the classifier function are then computed with respect to these M sequences. These gradients act as a guiding force, modifying the unconditional velocity field to steer the generation process towards sequences that achieve optimal classifier scores. In essence, STGFlow leverages straight-through gradient estimators to efficiently guide the generation towards high-scoring sequences during inference.
read the caption
Figure 2: Straight-Through Guided Flows (STGFlow). We compute the gradients of the classifier function with respect to M𝑀Mitalic_M discrete sequences sampled from the intermediate token distribution 𝐱tsubscript𝐱𝑡\mathbf{x}_{t}bold_x start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT, which act as a guided flow velocity that steers the unconditional trajectory towards sequences with optimal scores.

🔼 This figure showcases three examples of protein structures generated using the Gumbel-Softmax Flow Matching method. Each structure is accompanied by its predicted pLDDT, pAE, and pTM scores, all generated using the ESMFold prediction model. These metrics assess the quality of the predicted structures, with higher pLDDT scores indicating higher confidence in the prediction, lower pAE scores suggesting better accuracy in the relative positioning of amino acid residues, and higher pTM scores signifying a greater agreement with known protein structures.
read the caption
Figure 3: Predicted structures of de novo generated proteins from Gumbel-Softmax FM. The structures, pLDDT, pAE, and pTM scores are predicted with ESMFold [27]

🔼 This figure showcases three examples of novel peptide binders generated using the Gumbel-Softmax Flow Matching method. Each panel (A, B, C) represents a different target protein associated with a rare disease: JPH3 (Huntington’s Disease-Like 2), GFAP (Alexander Disease), and eIF2B (Vanishing White Matter Disease). For each target, the figure displays the 3D structure of the designed peptide binder, its amino acid sequence length (10 amino acids in A and B, 7 amino acids in C), and its binding interaction with the target protein (visualized via polar contacts within 3.5 Å). The protein structures shown in (A) were produced using AlphaFold3 predictions, while panels (B) and (C) utilize existing PDB structures (6A9P and 6CAJ, respectively). These results highlight the method’s capability to generate effective peptide binders for various disease-related targets without prior knowledge of existing binders, paving the way for potential therapeutic developments. Further details about additional targets are provided in Table 4 of the paper.
read the caption
Figure 4: Gumbel-Softmax FM generated peptide binders for three targets with no known binders. (A) 10101010 a.a. designed binder to JPH3 (structure generated with AlphaFold3) involved in Huntington’s Disease-Like 2. (B) 10101010 a.a. designed binder to GFAP (PDB: 6A9P) involved in Alexander Disease. (C) 7777 a.a. designed binder to eIF2B (PDB: 6CAJ) involved in Vanishing White Matter Disease. Docked with AutoDock VINA and polar contacts within 3.53.53.53.5 Å are annotated. Additional targets are shown in Table 4.

🔼 Figure 5 displays a comparison of peptide binders for protein 4EZN, illustrating the performance of Gumbel-Softmax FM in designing novel binders. The figure shows two peptide binders docked to protein 4EZN: an existing binder (green) and a de novo designed binder generated by Gumbel-Softmax FM (magenta). Key features of the figure are the improved docking scores of the designed binder (-6.5 kcal/mol) compared to the existing binder (-4.1 kcal/mol), highlighting its stronger binding affinity. Additionally, crucial polar contacts (within 3.5 Å) between the designed binder and protein 4EZN are annotated, providing insights into the binding interaction. Further comparisons of existing and designed peptide binders for different proteins are provided in Table 3 of the paper.
read the caption
Figure 5: Comparison of existing and Gumbel-Softmax FM designed binder to protein 4EZN. AutoDock VINA docking score of the designed binder (−6.56.5-6.5- 6.5 kcal/mol; magenta) is lower than that of the existing binder (−4.14.1-4.1- 4.1 kcal/mol; green) indicating stronger binding affinity. Polar contacts within 3.53.53.53.5 Å are annotated. Additional comparisons of existing and designed binders are in Table 3.

🔼 This figure visualizes the performance of Gumbel-Softmax Flow Matching (FM), a generative model for peptide design, enhanced with Straight-Through Guided Flows (STGFlow). The plots show how the predicted binding affinity of generated peptides changes over the course of the iterative generation process. Specifically, the model samples multiple (M) peptide sequences at each step, and their average predicted binding affinity is calculated and plotted. Crucially, the gradients of these predicted affinities guide the model’s next step, ensuring that the generation process is steered towards higher-affinity peptides. The graphs illustrate this guided optimization, showing how the predicted affinity increases over the iterations, driven by the STGFlow mechanism. Two specific target proteins, 3EQS and GFAP, are depicted, demonstrating the model’s effectiveness for different targets.
read the caption
Figure 6: Predicted binding-affinity scores over iteration of Gumbel-Softmax FM guided with STGFlow for target-binding peptide generation. The predicted binding affinity is the mean regression scores of the M𝑀Mitalic_M discrete sequences sampled at each integration step. The gradients of the scores are used to compute the guided velocity.

🔼 This figure displays the validation mean squared error (MSE) loss during training for a toy experiment involving different simplex dimensions. Two methods are compared: Fisher Flow Matching (FM) and Gumbel-Softmax FM. Both methods used the same loss calculation, yet the Fisher FM model shows significantly higher validation MSE loss, indicating a tendency to overfit the training data. This suggests that the parameterization used by Fisher FM is more prone to overfitting than the one used by Gumbel-Softmax FM.
read the caption
Figure 7: Validation MSE loss over training step of simplex-dimension toy experiment. Fisher FM exhibits significantly higher validation MSE loss during training than Gumbel-Softmax FM despite the same loss calculation, suggesting that the parameterization easily overfits to training data.

🔼 Figure 8 showcases three examples of novel peptide binders generated using the Gumbel-Softmax Flow Matching method. These peptides target proteins associated with rare diseases, for which no known binders previously existed. Each panel (A, B, C) highlights a different protein-peptide pair: (A) a 7-amino acid peptide binding to NPC2 (a protein involved in Niemann-Pick Disease Type C; PDB ID: 6W5V), (B) a 10-amino acid peptide binding to BMI1 (implicated in medulloblastoma; PDB ID: 2CKL), and (C) a 10-amino acid peptide binding to Gigaxonin (associated with Giant Axonal Neuropathy; PDB ID: 3HVE). The figure illustrates the binding interactions using AutoDock Vina docking, showing polar contacts within 3.5 angstroms (Å) of the binding site. Additional examples of generated peptide binders can be found in Table 4 of the paper.
read the caption
Figure 8: Gumbel-Softmax FM generated peptide binders for three targets with no known binders. (A) 7 a.a. designed binder to NPC2 (PDB: 6W5V) involved in Niemann-Pick Disease Type C. (B) 10 a.a. designed binder to BMI1 (PDB: 2CKL) involved in Medulloblastoma. (C) 10 a.a. designed binder to Gigaxonin (PDB: 3HVE) involved in Giant Axonal Neuropathy. Docked with AutoDock VINA and polar contacts within 3.5 Å are annotated. Additional targets are shown in Table 4.

🔼 This figure shows the 3D structures of 20 de novo generated proteins predicted by the Gumbel-Softmax Flow Matching (FM) model. Each protein structure is displayed in a different orientation and coloring scheme, highlighting their structural diversity. The proteins show various shapes, sizes, and folds, demonstrating the model’s ability to generate a wide range of diverse protein structures.
read the caption
Figure 9: Predicted structures of de novo generated proteins with Gumbel-Softmax FM. Generated proteins demonstrate diverse structural generation.
More on tables
| Model | Params () | pLDDT () | pTM () | pAE () | Entropy () | Diversity (%) () |
|---|---|---|---|---|---|---|
| Test Dataset (random 1000) | - | 74.00 | 0.63 | 12.99 | 4.0 | 71.8 |
| EvoDiff | 640M | 31.84 | 0.21 | 24.76 | 4.05 | 93.2 |
| ProtGPT2 | 738M | 54.92 | 0.41 | 19.39 | 3.85 | 70.9 |
| ProGen2-small | 151M | 49.38 | 0.28 | 23.38 | 2.55 | 89.3 |
| Gumbel-Softmax Flow Matching (Ours) | 198M | 52.54 | 0.27 | 16.67 | 3.41 | 86.1 |
| Gumbel-Softmax Score Matching (Ours) | 198M | 49.40 | 0.29 | 15.71 | 3.37 | 82.5 |
🔼 This table presents a comparison of various protein sequence generation models, evaluating their performance based on several key metrics. The models compared include EvoDiff and ProtGPT2, along with the proposed Gumbel-Softmax Flow Matching and Gumbel-Softmax Score Matching. For each model, 100 protein sequences were generated without any input conditioning (unconditionally). The table then assesses the quality of these generated sequences using metrics such as PLDDT (a measure of local structural confidence), PTM (predicted template modeling score for global structure quality), PAE (predicted alignment error, measuring pairwise residue placement accuracy), entropy (reflecting sequence diversity), and the percentage of diverse sequences generated.
read the caption
Table 2: Evaluation metrics for generative quality of protein sequences. Metrics were calculated on 100 unconditionally generated sequences from each model, including EvoDiff and ProtGPT2. The arrow indicates whether (↑)↑(\uparrow)( ↑ ) or (↓)↓(\downarrow)( ↓ ) values are better.
| PDB ID | existing binder | ipTM () | pTM () | VINA Docking Score (kcal/mol) () | |||
|---|---|---|---|---|---|---|---|
| existing | designed | existing | designed | existing | designed | ||
| GLP-1R (3C5T) | HXEGTFTSDVSSYLEGQAAKEFIAWLVRGRG | * | 0.65 | * | 0.66 | -5.7 | -7.5 |
| 1AYC | ARLIDDQLLKS | 0.68 | 0.67 | 0.88 | 0.88 | -5.3 | -4.6 |
| 2Q8Y | ALRRELADW | 0.44 | 0.70 | 0.83 | 0.84 | -6.7 | -6.8 |
| 3EQS | GDHARQGLLALG | 0.80 | 0.71 | 0.88 | 0.86 | -4.4 | -4.7 |
| 3NIH | RIAAA | 0.85 | 0.86 | 0.91 | 0.90 | -6.2 | -5.7 |
| 4EZN | VDKGSYLPRPTPPRPIYNRN | 0.54 | 0.59 | 0.85 | 0.87 | -4.1 | -6.5 |
| 4GNE | ARTKQTA | 0.89 | 0.76 | 0.76 | 0.76 | -5.0 | -4.8 |
| 4IU7 | HKILHRLLQD | 0.93 | 0.79 | 0.91 | 0.94 | -4.6 | -5.9 |
| 5E1C | KHKILHRLLQDSSS | 0.83 | 0.80 | 0.91 | 0.91 | -4.3 | -5.1 |
| 5EYZ | SWESHKSGRETEV | 0.73 | 0.81 | 0.77 | 0.78 | -2.9 | -6.9 |
| 5KRI | KHKILHRLLQDSSS | 0.83 | 0.77 | 0.91 | 0.91 | -3.5 | -5.5 |
| 7LUL | RWYERWV | 0.94 | 0.91 | 0.93 | 0.92 | -6.5 | -7.6 |
| 8CN1 | ETEV | 0.90 | 0.86 | 0.72 | 0.82 | -6.0 | -6.9 |
🔼 This table compares the performance of existing peptide binders and those designed using the Gumbel-Softmax Flow Matching (FM) method. For each of several protein targets, it shows the interface predicted template modeling (ipTM) scores and VINA docking scores for both existing binders (from the literature) and newly designed binders (generated by the model). ipTM assesses the accuracy of predicted relative positions of interacting residues between the peptide and protein, while VINA docking score estimates the binding affinity. Higher ipTM scores and lower VINA scores indicate better binding. Note that one entry contains an unnatural amino acid (marked with *) which cannot be processed by AlphaFold3, and thus lacks ipTM data.
read the caption
Table 3: Comparison of ipTM and VINA docking scores for existing and designed peptide binders to protein targets. The ipTM scores are calculated by AlphaFold3 for peptide-protein complexes using both existing peptides and peptides designed by guided Gumbel-Softmax FM. *Contains unnatural amino acid X which cannot be processed by AlphaFold3.
| PDB ID | Protein Name | Disease | ipTM () | pTM () | VINA Docking Score (kcal/mol) () | |||
|---|---|---|---|---|---|---|---|---|
| designed | scramble | designed | scramble | designed | scramble | |||
| 6A9P | GFAP | Alexander Disease | 0.62 | 0.38 | 0.31 | 0.29 | -5.9 | -3.7 |
| 6CAJ | eIF2B | Vanishing White Matter Disease | 0.61 | 0.39 | 0.77 | 0.76 | -9.1 | -9.0 |
| 3HVE | Gigaxonin | Giant Axonal Neuropathy | 0.75 | 0.54 | 0.83 | 0.82 | -6.8 | -6.2 |
| 6W5V | NPC2 | Niemann-Pick Disease Type C | 0.80 | 0.34 | 0.79 | 0.77 | -6.5 | -5.6 |
| JPH3 | Huntington’s Disease-Like 2 (HDL2) | 0.72 | 0.60 | 0.49 | 0.49 | -7.9 | -7.8 | |
| 2CKL | BMI1 | Medulloblastoma | 0.71 | 0.43 | 0.81 | 0.73 | -6.8 | -6.2 |
🔼 This table presents a comparison of the binding affinity of designed peptides and scrambled control peptides for six protein targets with no known binders. The performance is evaluated using three metrics: ipTM (interface predicted template modeling) score from AlphaFold3, which measures the accuracy of the predicted relative positions between residues involved in peptide-protein interactions; pTM (predicted template modeling) score from AlphaFold3, which measures the accuracy of the predicted structure of the whole peptide-protein complex; and VINA docking score from AutoDock Vina, which evaluates the free energy of the binding interaction. The ipTM and pTM scores are calculated using AlphaFold3, while the VINA docking score is determined using AutoDock Vina. For comparison, scrambled sequences (negative controls) are generated by randomly permuting the designed peptide sequences. The table includes the PDB ID, protein name, disease associated with the protein, ipTM score, pTM score, and VINA docking score for both the designed peptides and the scrambled controls. A note indicates that AlphaFold3-predicted structures were used for docking when PDB structures were not available.
read the caption
Table 4: Comparison of ipTM and VINA docking scores for designed peptide binders and scrambled negative control to protein targets with no known binders. The ipTM and pTM scores are calculated by AlphaFold3 and docking scores are calculated by AutoDock VINA for peptides designed by Gumbel-Softmax FM with STGFlow. Designed sequences are randomly permuted to generate a scrambled negative control for comparison. *No PDB structure available. Used AlphaFold3 predicted structure for docking.
| Layers | Input Dimension | Output Dimension |
|---|---|---|
| Sequence Distribution Embedding Module | vocab size | 1024 |
| Feed-Forward + GeLU | vocab size | 1024 |
| DiT Blocks | ||
| Adaptive Layer Norm (time conditioning) | 1024 | 1024 |
| Multi-Head Self-Attention () | ||
| + Rotary Positional Embeddings | 1024 | 1024 |
| Dropout + Residual | 1024 | 1024 |
| Adaptive Layer Norm (time conditioning) | 1024 | 1024 |
| FFN + GeLU | 1024 | 1024 |
| DiT Final Block | ||
| Adaptive Layer Norm (time conditioning) | 1024 | 1024 |
| Linear | 1024 | vocab size |
🔼 This table details the architecture of the Diffusion Transformer model used in the paper. It breaks down the model into its main components: Sequence Distribution Embedding Module, DiT Blocks (repeated 32 times), and DiT Final Block. Each layer’s input and output dimensions are specified, along with the layers within each block: Feed-Forward, GeLU activation, Adaptive Layer Normalization (with time conditioning), Multi-Head Self-Attention (with 16 attention heads and Rotary Positional Embeddings), Dropout, Residual connections, and a final linear layer. This provides a comprehensive view of the model’s internal structure and its processing of information at each stage.
read the caption
Table 5: Diffusion Transformer Architecture
| Layers | Protein Dimension | Peptide Dimension |
|---|---|---|
| Embedding Module | ||
| CNN Layers (Kernel Sizes: 3,5,7) | per kernel | |
| ReLU Activation | per kernel | per kernel |
| Global Pooling (Max + Avg) | ||
| Linear Layer | ||
| Layer Norm | ||
| Cross-Attention | ||
| Multi-Head Attention () | ||
| Linear Layer | ||
| ReLU | ||
| Dropout | ||
| Linear Layer | ||
| Shared Prediction Head | ||
| Linear Layer | ||
| ReLU | ||
| Dropout | ||
| Regression Head | ||
🔼 This table details the architecture of the peptide-binding affinity classifier used in the paper. It’s a multi-head cross-attention network that uses ESM-2 650M protein and peptide sequence embeddings as input. The network is designed to predict binding affinity scores (regression) and classify affinities into three categories (classification): low, medium, and high. The architecture includes convolutional layers, layer normalization, attention mechanisms, and dropout for regularization. The output is a single value representing the predicted binding affinity or a class label.
read the caption
Table 6: Peptide-Binding Affinity Classifier
| Simplex Dimension | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 512 |
|---|---|---|---|---|---|---|---|---|---|
| Linear FM | 0.013 | 0.046 | 0.070 | 0.100 | 0.114 | 0.112 | 0.156 | 0.146 | 0.479 |
| Dirichlet FM | 0.007 | 0.017 | 0.032 | 0.035 | 0.028 | 0.024 | 0.039 | 0.053 | 0.554 |
| Fisher FM (Optimal Transport) | 0.0004 | 0.007 | 0.007 | 0.007 | 0.008 | 0.043 | 0.013 | 0.013 | 0.036 |
| Gumbel-Softmax FM (Ours) | 0.029 | 0.027 | 0.025 | 0.027 | 0.030 | 0.029 | 0.035 | 0.038 | 0.048 |
🔼 This table presents a quantitative comparison of the performance of several generative models on a synthetic sequence generation task. The models were evaluated using the KL divergence metric, which measures the difference between the probability distributions of generated sequences and the ground truth distribution. The experiment was designed to test the scalability of the different approaches to higher-dimensional sequence spaces (simplex dimensions). All models were trained on 100,000 sequences of length 4, sampled from a random distribution. The KL divergence was calculated on 51,200 sequences generated after 50,000 training steps for each model. The results allow for an assessment of how well each model can learn to generate sequences and how well that performance scales with the complexity of the sequence space.
read the caption
Table 7: KL divergences of toy experiment for increasing simplex dimensions compared to benchmark models. The sequence length is set to a constant of 4 across all experiments. The toy models are trained on 100K sequences from a random distribution. KL divergence is evaluated for 51.2K sequences after 50K training steps.
Full paper#