TL;DR#
Recent robot vision-language-action models show generalization, but action heads limit adaptability to diverse action spaces. The models’ reliance on compact action heads constrains adaptability to heterogeneous action spaces. Addressing this, Dita introduces a framework for directly denoising continuous action sequences using a multimodal diffusion process. Dita leverages Transformer architectures to enhance scalability, integrating diverse datasets across sensors, tasks & action spaces.
Unlike prior methods with shallow networks, Dita uses in-context conditioning for fine-grained alignment between denoised actions & raw visual tokens, modeling action deltas & environmental nuances. Evaluations show state-of-the-art performance in simulation & robust real-world adaptation with only 10-shot finetuning, making Dita a versatile & lightweight baseline for generalist robot policy learning.
Key Takeaways#
Why does it matter?#
This paper is important for researchers because Dita streamlines robot learning with a simple, scalable architecture, achieving strong results with minimal data and opening new possibilities for generalist robotic policies in complex environments.
Visual Insights#

🔼 Figure 1 illustrates three different approaches to building generalist robot policy architectures. The leftmost architecture represents traditional robot transformers that utilize discrete actions. Examples include Robot Transformer and OpenVLA. The middle architecture shows a transformer with a diffusion action head. This approach denoises continuous actions using a small network conditioned on embeddings from a causal transformer. Octo and π0 are examples of this approach. The rightmost architecture is the proposed Dita architecture. Dita denoises actions directly within the context of its conditioning.
read the caption
Figure 1: Illustrations of different generalist robot policy architectures. Left head: the common robot Transformer architecture with discretization actions, e.g., Robot Transformer [8, 9] and OpenVLA [32]. Middle head: the Transformer architecture with diffusion action head which denoises the individual continuous action with a small network condition on each embedding from the causal Transformer, e.g., Octo [72] and π0subscript𝜋0\pi_{0}italic_π start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT [5]. Right head: the proposed Dita architecture that denoises actions inherently in an in-context conditioning style.
| Method | cokecan | movenear | drawer | |||
|---|---|---|---|---|---|---|
| match | variant | match | variant | match | variant | |
| RT-1-X [8] | 56.7% | 49.0% | 31.7% | 32.3% | 59.7% | 29.4% |
| Octo-Base [72] | 17.0% | 0.6% | 4.2% | 3.1% | 22.7% | 1.1% |
| OpenVLA-7B [32] | 16.3% | 54.5% | 46.2% | 47.7% | 35.6% | 17.7% |
| Dita (Ours) | 83.7% | 85.5% | 76.0% | 73.0% | 46.3% | 37.5% |
🔼 This table presents a comparison of success rates achieved by four different methods (RT-1-X, Octo-Base, OpenVLA-7B, and Dita) on the SimplerEnv benchmark. SimplerEnv tests robot control policies across a set of tasks. The table shows results for both ‘match’ and ‘variant’ versions of the Google Robot tasks. The ‘match’ versions represent tasks performed under standard conditions, whereas the ‘variant’ versions involve changes to task parameters, adding to the challenge. This allows for an assessment of how well each method generalizes to slightly different, more realistic situations.
read the caption
Table 1: Success rate comparison with RT-1-X [8], Octo-Base [72] and OpenVLA-7B [32] on SimplerEnv (both match and variant results of Google Robot [8]).
In-depth insights#
In-Context DiT#
In-Context Diffusion Transformers (DiT) represent a paradigm shift in robot learning, moving beyond traditional methods by leveraging the power of Transformer architectures for direct action sequence denoising. Unlike prior approaches that rely on shallow networks for conditioning denoising, In-Context DiT emphasizes fine-grained alignment between denoised actions and raw visual tokens from historical observations. This explicit modeling of action deltas and environmental nuances allows the model to effectively capture subtle relationships, resulting in improved robustness and adaptability. It offers a pathway to create versatile robot policies capable of excelling across diverse tasks and environmental settings.
Cross-Embodiment#
Cross-embodiment is a critical challenge in robotics, demanding that a policy trained on one robot can effectively control others. This often involves adapting to different kinematics, actuation methods, and sensor suites. A key approach is to learn invariant representations of tasks and environments that are independent of the specific robot. Domain adaptation techniques can further bridge the gap between simulated and real robots. Successfully tackling cross-embodiment leads to more generalizable and robust robotic systems, capable of quickly adapting to new platforms and tasks. Data augmentation and transfer learning also play a vital role in cross-embodiment strategies.
Long-Horizon Tasks#
Long-horizon tasks in robotics present a significant challenge, demanding robust planning and execution over extended timeframes. These tasks often require intricate sequences of actions, such as those described in the paper involving opening drawers, manipulating objects, and achieving complex arrangements. The difficulty lies in maintaining accuracy and stability throughout the entire process, as errors accumulate and can derail the task. Successfully tackling long-horizon tasks necessitates models with strong memory, reasoning, and error-correction capabilities. Furthermore, robustness to environmental variations and unexpected events is crucial for reliable performance. The paper highlights the importance of addressing these challenges to enable robots to perform more complex and useful tasks in real-world scenarios. One key aspect involves effectively modeling action deltas and environmental nuances. This is critical for anticipating and adapting to changes during task execution. Success is related to model’s ability to manage intricate, extended-horizon tasks, demonstrating its ability to generalize.
Camera Generalize#
While the term “Camera Generalize” isn’t explicitly present, the paper strongly emphasizes robustness to novel camera views as a critical aspect of generalist robot policies. The ManiSkill2 benchmark is used to evaluate performance with 300K random cameras, where Dita consistently exhibits superior performance compared to baselines. This implies the model effectively extracts viewpoint-invariant features, likely through techniques like data augmentation with varied camera perspectives during training or architectural designs inherently robust to viewpoint changes. The ability to generalize across camera views is crucial for real-world deployment, where the robot’s viewpoint may differ significantly from the training data. Further exploration into how Dita achieves this robustness, perhaps by analyzing its feature representations or attention patterns, would be valuable for understanding and improving generalization capabilities.
Scalable VLAs#
The concept of “Scalable VLAs” (Vision-Language-Action models) underscores a critical need in robotics and AI: the ability to generalize learned behaviors across diverse environments, robots, and tasks. Scalability in VLAs implies several key attributes: the model’s capacity to handle increasing amounts of data without performance degradation, its adaptability to new robotic platforms with varying action spaces, and its robustness to different sensory inputs (camera views, lighting). Achieving this necessitates architectures that can efficiently integrate information from visual and linguistic modalities. Furthermore, a scalable VLA should exhibit few-shot or zero-shot transfer learning capabilities, enabling rapid adaptation to novel tasks with minimal task-specific training. This often involves pre-training on large, diverse datasets and employing techniques like meta-learning or domain adaptation to bridge the gap between training and deployment environments. Ultimately, the goal is to create a VLA that can serve as a general-purpose robot controller, capable of performing a wide range of tasks in unstructured, real-world settings.
More visual insights#
More on figures
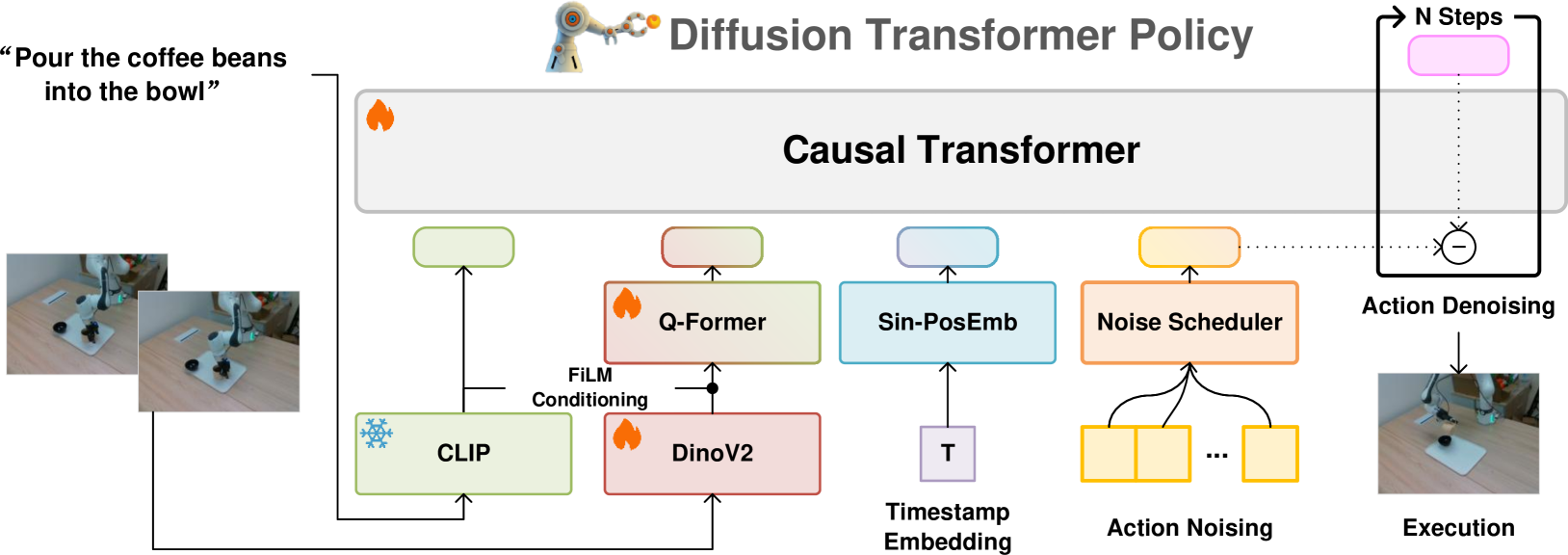
🔼 This figure illustrates the architecture of Dita, a Transformer-based diffusion model for generalist robotic learning. Language instructions are processed by a pretrained CLIP model to generate instruction tokens. Image observations are encoded using a pretrained DINOv2 model, and a Q-Former network selects relevant image features based on the instruction context. These instruction tokens, image features, timestep embeddings, and a noised version of the action are concatenated into a single sequence. This sequence is then fed into a causal Transformer network, which denoises the action sequence to generate the final, refined action.
read the caption
Figure 2: Our model employs a Transformer-based diffusion architecture, integrating a pretrained CLIP network to extract language instruction tokens. The DinoV2 [53] model encodes image observations, followed by a Q-Former that queries features for each image. The instruction tokens, image features, timestep embeddings, and noised action are concatenated to construct a token sequence, which is then fed into the network to denoise the raw actions.

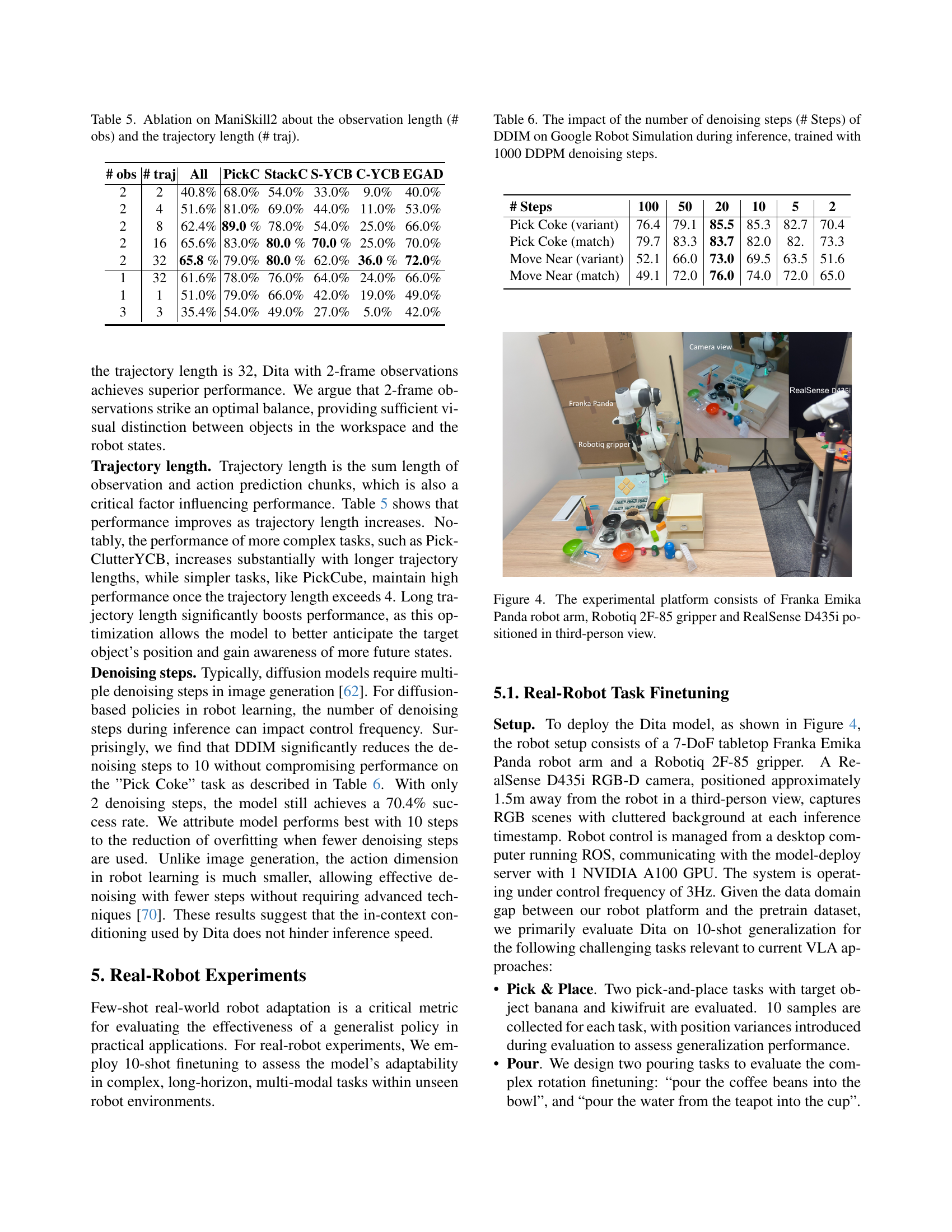
🔼 The figure shows the experimental setup used for the real-robot experiments. It consists of a Franka Emika Panda robot arm equipped with a Robotiq 2F-85 gripper. A RealSense D435i depth camera is positioned to provide a third-person view of the robot’s workspace, capturing RGB-D images during the experiments. This setup enables the robot to perform various manipulation tasks while the camera provides visual input for the vision-language-action model.
read the caption
Figure 3: The experimental platform consists of Franka Emika Panda robot arm, Robotiq 2F-85 gripper and RealSense D435i positioned in third-person view.

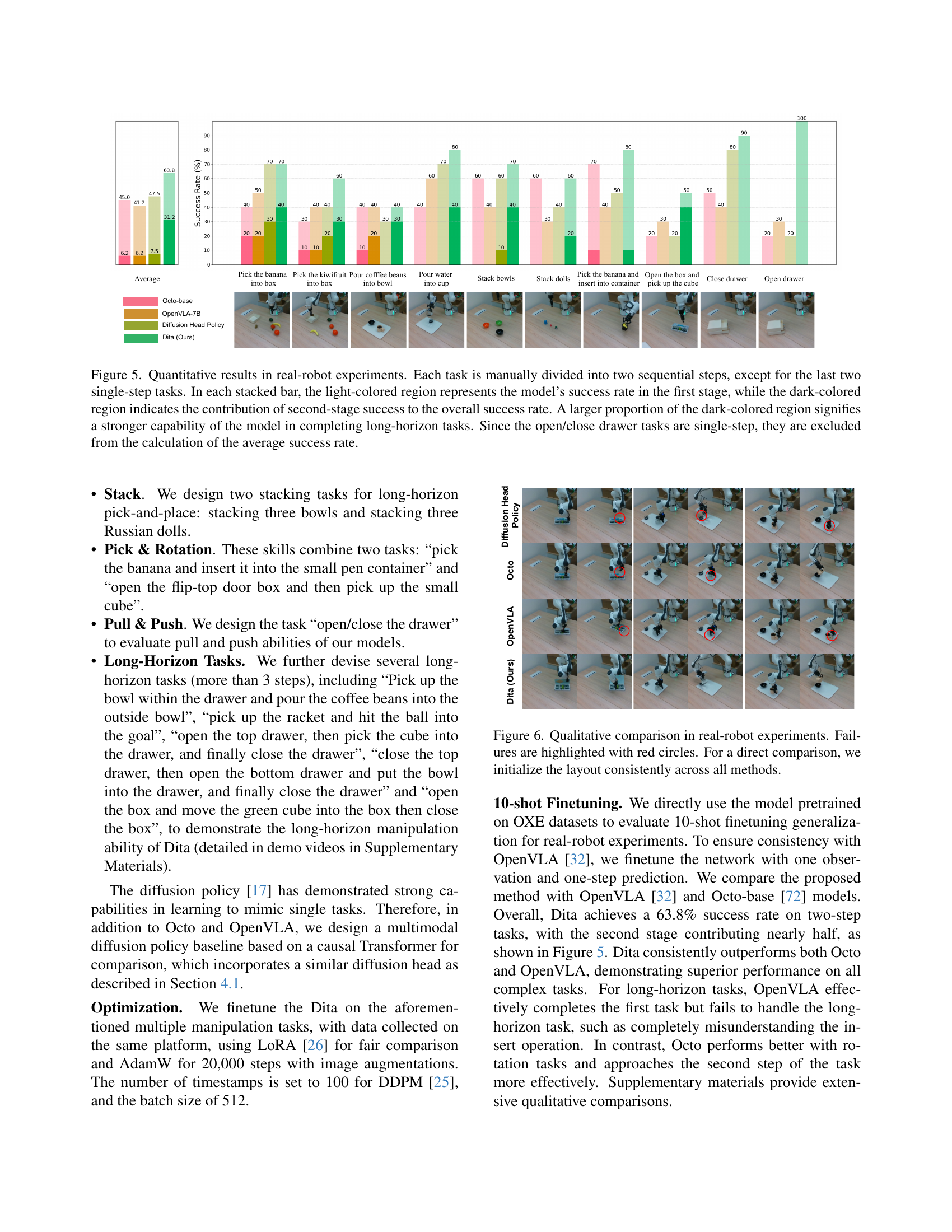
🔼 This figure presents quantitative results from real-robot experiments evaluating the success rate of different tasks. Each task is broken down into two sequential steps (except for the last two, which are single-step). The stacked bars visualize the success rate: the light-colored portion shows the first-stage success, and the dark-colored portion represents the contribution of the second stage to the overall success. A larger dark-colored area indicates better performance on long-horizon tasks. Single-step tasks (opening/closing drawers) are excluded from the average success rate calculation.
read the caption
Figure 4: Quantitative results in real-robot experiments. Each task is manually divided into two sequential steps, except for the last two single-step tasks. In each stacked bar, the light-colored region represents the model’s success rate in the first stage, while the dark-colored region indicates the contribution of second-stage success to the overall success rate. A larger proportion of the dark-colored region signifies a stronger capability of the model in completing long-horizon tasks. Since the open/close drawer tasks are single-step, they are excluded from the calculation of the average success rate.

🔼 This figure presents a qualitative comparison of Dita’s performance against other methods (Octo, OpenVLA, and a diffusion head policy baseline) in real-world robotic experiments. The image shows the results of several trials, with failures indicated by red circles. Notably, all methods started from the same initial setup, providing a direct visual comparison of their ability to successfully complete a series of manipulation tasks.
read the caption
Figure 5: Qualitative comparison in real-robot experiments. Failures are highlighted with red circles. For a direct comparison, we initialize the layout consistently across all methods.

🔼 This figure showcases the robustness of the Dita model across various challenging conditions. It presents qualitative results demonstrating the model’s ability to successfully complete tasks even with changes in background, object arrangements, and lighting. Each row represents a different task performed by the robot under these varied conditions, visually demonstrating the model’s generalizability and resilience.
read the caption
Figure 6: Qualitative results of Dita under variances in Google Robot.

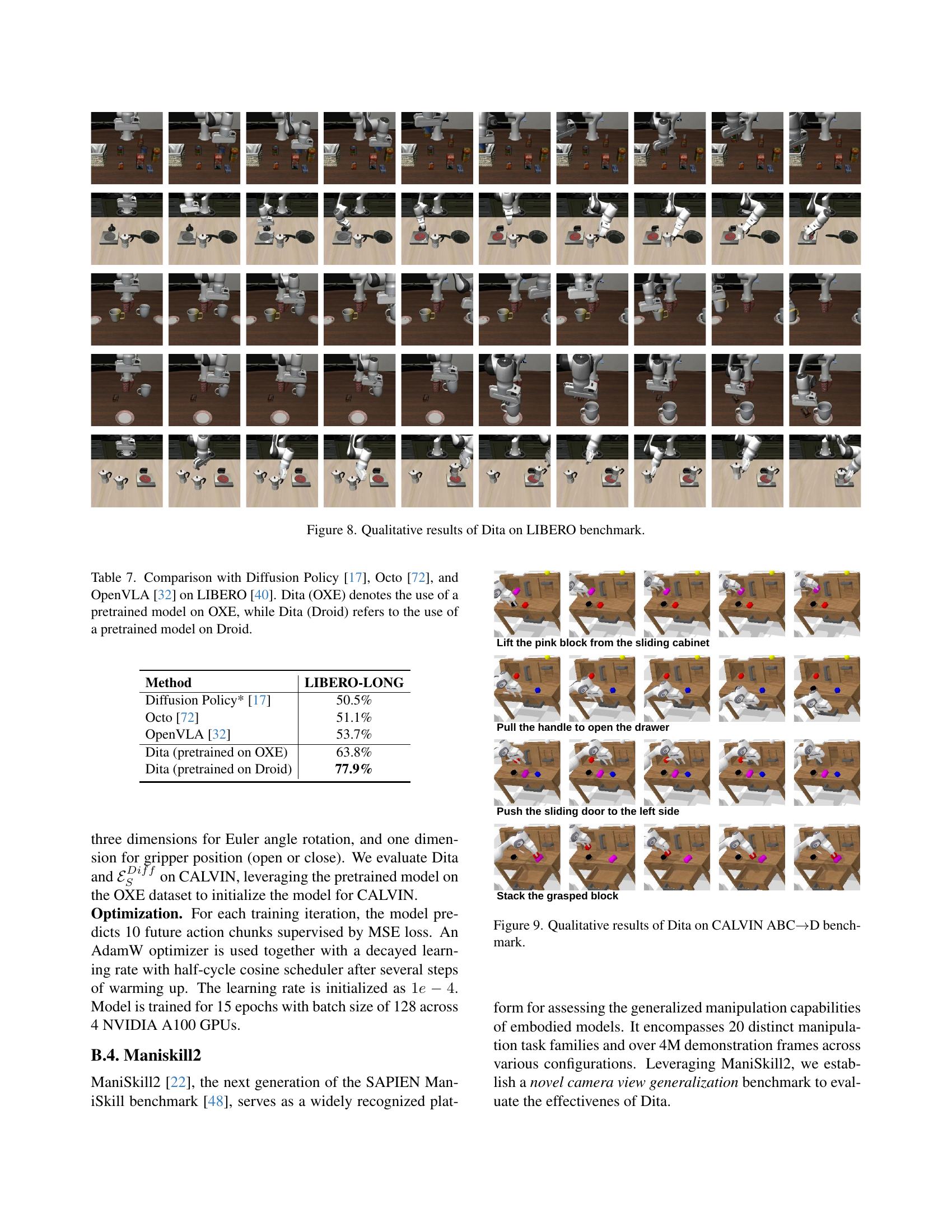
🔼 This figure showcases qualitative results obtained by Dita on the LIBERO benchmark. It provides a visual comparison of Dita’s performance across various tasks within the LIBERO dataset, illustrating the model’s ability to handle diverse scenarios and object interactions. The images likely demonstrate successful and unsuccessful attempts at completing tasks, highlighting Dita’s strengths and weaknesses in different contexts.
read the caption
Figure 7: Qualitative results of Dita on LIBERO benchmark.

🔼 This figure showcases qualitative results from the CALVIN ABC→D benchmark, demonstrating the performance of the Dita model on long-horizon tasks. Each row represents a distinct task, illustrating the model’s ability to successfully complete complex sequences of actions. The images depict both successful and failed attempts, offering a visual comparison of Dita’s capabilities and robustness across a range of manipulations.
read the caption
Figure 8: Qualitative results of Dita on CALVIN ABC→→\rightarrow→D benchmark.

🔼 This figure presents a qualitative comparison of the performance of the proposed Dita model and a baseline diffusion action head model on the ManiSkill2 benchmark’s PickClutterYCB task. It visually showcases the results, allowing for a direct comparison of the model’s ability to successfully complete the task. The top row illustrates Dita’s execution, while the bottom row displays the results of the baseline diffusion action head model. This comparison highlights the differences in the approach taken by each model to complete the task and the resulting successes and failures.
read the caption
Figure 9: Qualitative comparison between Dita (top) and Diffusion Action Head baseline ℰθ∼sDiffsuperscriptsubscriptℰsimilar-to𝜃𝑠𝐷𝑖𝑓𝑓\mathcal{E}_{\theta\sim s}^{Diff}caligraphic_E start_POSTSUBSCRIPT italic_θ ∼ italic_s end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_D italic_i italic_f italic_f end_POSTSUPERSCRIPT (bottom) on ManiSkill2 (PickClutterYCB).

🔼 This figure displays a comparison of the convergence speed between two different approaches for training a robot policy: the DiT (Diffusion Transformer) Policy and a simpler Diffusion Action Head strategy. Both methods were trained on the OXE dataset and used the same number of parameters for a fair comparison. The x-axis represents the training steps, while the y-axis shows the MSE (Mean Squared Error) loss, a measure of the model’s error during training. The blue line illustrates the convergence of the DiT Policy, and the orange line shows the convergence of the Diffusion Action Head strategy. The graph visually demonstrates that the DiT Policy converges faster and achieves a lower MSE loss than the Diffusion Action Head approach.
read the caption
Figure 10: Convergence Analysis on OXE dataset [9]. The blue line is DiT Policy, and the orange line is Diffusion action head strategy with the same number of parameters.
More on tables
| Method | SPATIAL | OBJECT | GOAL | LONG | Averge |
|---|---|---|---|---|---|
| DP*[17] | 78.3% | 92.5% | 68.3% | 50.5% | 72.4% |
| Octo [72] | 78.9% | 85.7% | 84.6% | 51.1% | 75.1% |
| OpenVLA [32] | 84.9% | 88.4% | 79.2% | 53.7% | 76.5% |
| Dita (Ours) | 84.2% | 96.3% | 85.4% | 63.8% | 82.4% |
🔼 This table compares the performance of Dita against three other methods (Diffusion Policy, Octo, and OpenVLA) on the LIBERO benchmark. It focuses on four key aspects of robotic tasks within LIBERO: spatial reasoning, object manipulation, goal achievement, and long-horizon tasks. The results highlight Dita’s superior performance, particularly in long-horizon tasks which involve a sequence of actions. All results (except for Dita) are taken directly from the OpenVLA paper, ensuring consistency and facilitating direct comparison.
read the caption
Table 2: Comparison with Diffusion Policy (denoted as DP*, training from scratch) [17], Octo [72], and OpenVLA [32] on LIBERO [40]. Except for Dita results, all other results are sourced from [32].
| Method | Input | No. Instructions in a Row (1000 chains) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | Avg.Len. | ||
| RoboFlamingo [36] | S-RGB,G-RGB | 82.4% | 61.9% | 46.6% | 33.1% | 23.5% | 2.47 |
| GR-1 [78] | S-RGB,G-RGB,P | 85.4% | 71.2% | 59.6% | 49.7% | 40.1% | 3.06 |
| 3D Diffuser [30] | S-RGBD,G-RGBD,P,Cam | 92.2% | 78.7% | 63.9% | 51.2% | 41.2% | 3.27 |
| GR-MG [34] | S-RGBD,G-RGBD,P | 96.8% | 89.3% | 81.5% | 72.7% | 64.4 % | 4.04 |
| SuSIE [4] | S-RGB | 87.0% | 69.0% | 49.0% | 38.0% | 26.0% | 2.69 |
| GHIL-Glue [24, 4] | S-RGB | 95.2% | 88.5% | 73.2% | 62.5% | 49.8% | 3.69 |
| w/o Pretrain | S-RGB | 75.5% | 44.8% | 25.0% | 15.0% | 7.5% | 1.68 |
| S-RGB | 94.3% | 77.5% | 62.0% | 48.3% | 34.0% | 3.16 | |
| Ours w/o Pretrain | S-RGB | 89.5% | 63.3% | 39.8% | 27.3% | 18.5% | 2.38 |
| Ours | S-RGB | 94.5% | 82.5% | 72.8% | 61.3% | 50.0% | 3.61 |
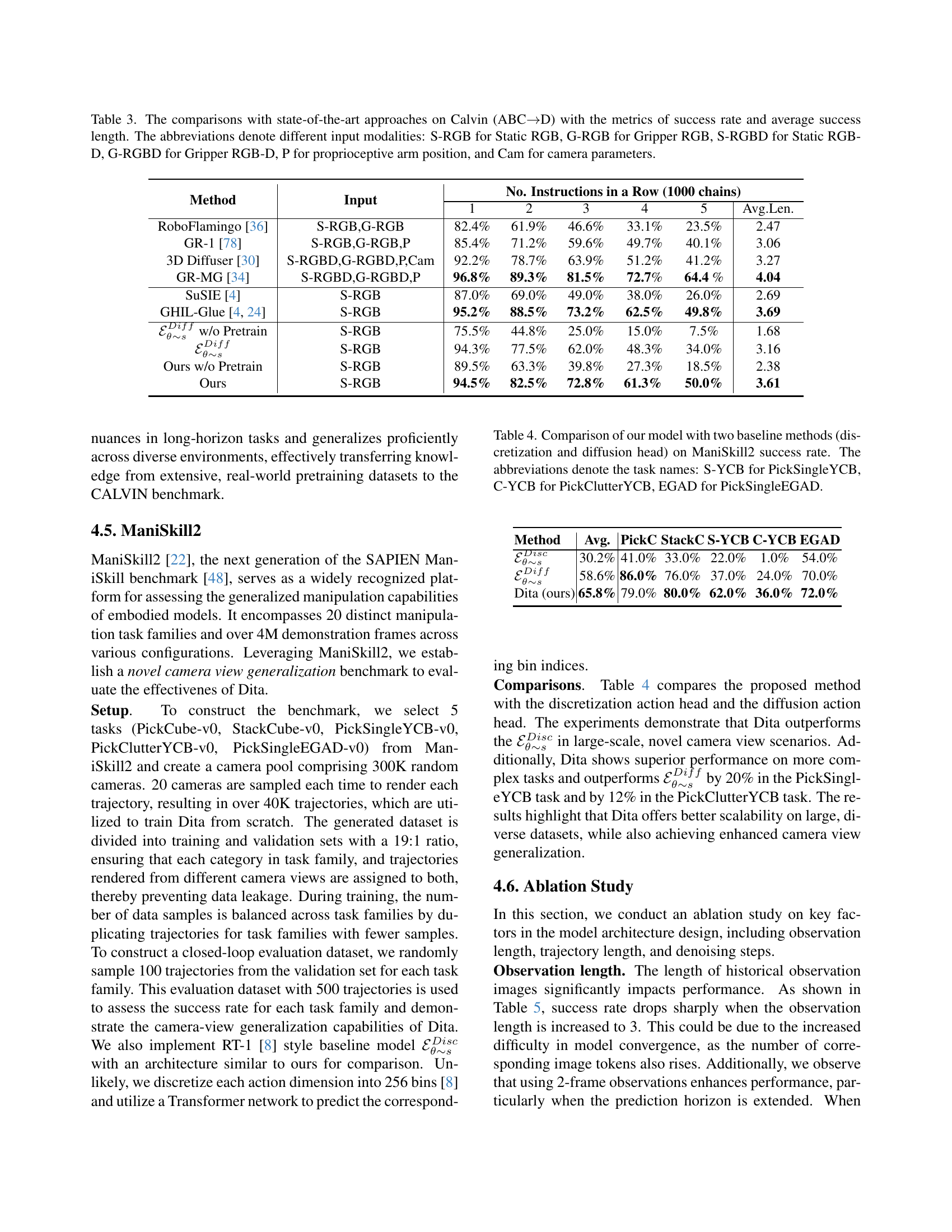
🔼 Table 3 presents a comparison of Dita’s performance with state-of-the-art approaches on the CALVIN benchmark (ABC→D). The CALVIN benchmark evaluates the ability of models to perform long-horizon, language-conditioned tasks across diverse scenarios. The table shows success rates and average success lengths for each method, broken down by the number of consecutive subtasks completed. Different input modalities used by each method are also indicated through abbreviations: S-RGB (Static RGB), G-RGB (Gripper RGB), S-RGBD (Static RGB-D), G-RGBD (Gripper RGB-D), P (Proprioceptive arm position), and Cam (Camera parameters). This allows for a detailed analysis of the relative strengths and weaknesses of different approaches in handling long-horizon tasks and diverse sensor inputs.
read the caption
Table 3: The comparisons with state-of-the-art approaches on Calvin (ABC→→\rightarrow→D) with the metrics of success rate and average success length. The abbreviations denote different input modalities: S-RGB for Static RGB, G-RGB for Gripper RGB, S-RGBD for Static RGB-D, G-RGBD for Gripper RGB-D, P for proprioceptive arm position, and Cam for camera parameters.
| Method | Avg. | PickC | StackC | S-YCB | C-YCB | EGAD |
|---|---|---|---|---|---|---|
| 30.2% | 41.0% | 33.0% | 22.0% | 1.0% | 54.0% | |
| 58.6% | 86.0% | 76.0% | 37.0% | 24.0% | 70.0% | |
| Dita (ours) | 65.8% | 79.0% | 80.0% | 62.0% | 36.0% | 72.0% |
🔼 This table presents a comparison of the success rates achieved by three different methods on the ManiSkill2 benchmark. The methods compared are: 1) the proposed Dita model; 2) a discretization-based baseline method; and 3) a diffusion-head baseline method. The ManiSkill2 benchmark includes several manipulation tasks, and the table shows the success rates for each method on five specific tasks: PickSingleYCB (S-YCB), PickClutterYCB (C-YCB), and PickSingleEGAD (EGAD). The results highlight the performance differences between the proposed method and the baseline methods in terms of achieving successful task completion.
read the caption
Table 4: Comparison of our model with two baseline methods (discretization and diffusion head) on ManiSkill2 success rate. The abbreviations denote the task names: S-YCB for PickSingleYCB, C-YCB for PickClutterYCB, EGAD for PickSingleEGAD.
| # obs | # traj | All | PickC | StackC | S-YCB | C-YCB | EGAD |
|---|---|---|---|---|---|---|---|
| 2 | 2 | 40.8% | 68.0% | 54.0% | 33.0% | 9.0% | 40.0% |
| 2 | 4 | 51.6% | 81.0% | 69.0% | 44.0% | 11.0% | 53.0% |
| 2 | 8 | 62.4% | 89.0 % | 78.0% | 54.0% | 25.0% | 66.0% |
| 2 | 16 | 65.6% | 83.0% | 80.0 % | 70.0 % | 25.0% | 70.0% |
| 2 | 32 | 65.8 % | 79.0% | 80.0 % | 62.0% | 36.0 % | 72.0% |
| 1 | 32 | 61.6% | 78.0% | 76.0% | 64.0% | 24.0% | 66.0% |
| 1 | 1 | 51.0% | 79.0% | 66.0% | 42.0% | 19.0% | 49.0% |
| 3 | 3 | 35.4% | 54.0% | 49.0% | 27.0% | 5.0% | 42.0% |
🔼 This table presents the results of an ablation study conducted on the ManiSkill2 benchmark to analyze the impact of observation length and trajectory length on model performance. Observation length refers to the number of consecutive frames used as input to the model, while trajectory length represents the total number of frames (including observations and actions) processed in a single prediction sequence. The table shows how varying these two factors affects the model’s ability to successfully complete various manipulation tasks within the ManiSkill2 benchmark, providing insights into the optimal configuration for achieving robust performance.
read the caption
Table 5: Ablation on ManiSkill2 about the observation length (# obs) and the trajectory length (# traj).
| # Steps | 100 | 50 | 20 | 10 | 5 | 2 |
|---|---|---|---|---|---|---|
| Pick Coke (variant) | 76.4 | 79.1 | 85.5 | 85.3 | 82.7 | 70.4 |
| Pick Coke (match) | 79.7 | 83.3 | 83.7 | 82.0 | 82. | 73.3 |
| Move Near (variant) | 52.1 | 66.0 | 73.0 | 69.5 | 63.5 | 51.6 |
| Move Near (match) | 49.1 | 72.0 | 76.0 | 74.0 | 72.0 | 65.0 |
🔼 This table shows the impact of varying the number of denoising steps during inference on the performance of the Dita model on the Google Robot Simulation benchmark. The model was initially trained using 1000 DDPM denoising steps. The table presents success rates for different tasks (‘Pick Coke’ match and variant, ‘Move Near’ match and variant) at various numbers of DDIM denoising steps during inference (100, 50, 20, 10, 5, 2). This allows for analysis of the trade-off between inference speed and accuracy.
read the caption
Table 6: The impact of the number of denoising steps (# Steps) of DDIM on Google Robot Simulation during inference, trained with 1000 DDPM denoising steps.
| Method | LIBERO-LONG |
|---|---|
| Diffusion Policy* [17] | 50.5% |
| Octo [72] | 51.1% |
| OpenVLA [32] | 53.7% |
| Dita (pretrained on OXE) | 63.8% |
| Dita (pretrained on Droid) | 77.9% |
🔼 This table compares the performance of Dita against three other state-of-the-art methods (Diffusion Policy, Octo, and OpenVLA) on the LIBERO benchmark. It shows success rates on the LIBERO-LONG sub-dataset. The results are presented for two versions of Dita: one pretrained on the OXE dataset and another pretrained on the Droid dataset. This highlights the impact of the pretraining dataset on the model’s performance.
read the caption
Table 7: Comparison with Diffusion Policy [17], Octo [72], and OpenVLA [32] on LIBERO [40]. Dita (OXE) denotes the use of a pretrained model on OXE, while Dita (Droid) refers to the use of a pretrained model on Droid.
| Strategy | No. Instructions in a Row (1000 chains) | |||||
| w lr decay | 94.5% | 82.5% | 72.8% | 61.3% | 50.0% | 3.61 |
| w/o lr decay | 91.8% | 80.0% | 68.0% | 56.9% | 45.9% | 3.43 |
🔼 This table presents an ablation study investigating the impact of different learning rate scheduling strategies on the performance of the Dita model within the CALVIN benchmark. It compares a strategy with learning rate decay against one without, showing the success rates achieved across various lengths of instruction sequences (number of instructions in a row). The results highlight the effect of the learning rate scheduler on the model’s ability to generalize and perform long-horizon tasks in the CALVIN environment.
read the caption
Table 8: The ablation study on the learning rate scheduler in the Calvin benchmark.
| Methods | No. Instructions in a Row (1000 chains) | |||||
| MDT* [61] | 61.7% | 40.6% | 23.8% | 14.7% | 8.7% | 1.54 |
| Unet1D head [17] | 76.8% | 46.5% | 28.8% | 18.5% | 10.0% | 1.80 |
| Transformer head [17] | 75.8% | 44.8% | 26.5% | 16.5% | 8.0% | 1.72 |
| 8-layer MLP head | 69.8% | 42.5% | 26.3% | 16.8% | 11.0% | 1.66 |
| 3-layer MLP head | 75.5% | 44.8% | 25.0% | 15.0% | 7.5% | 1.68 |
| Single token act chunks | 56.5% | 18.3% | 6.0% | 2.8% | 0.8% | 0.84 |
| Ours | 89.5% | 63.3% | 39.8% | 27.3% | 18.5% | 2.38 |
🔼 Table 9 presents a comparison of different action design approaches on the CALVIN (ABC→D) benchmark, excluding any model pretraining. It contrasts several methods, including a baseline using an 8-layer Multilayer Perceptron (MLP), a 3-layer MLP, a Transformer-based approach, and a Unet-1D architecture, all without any pretraining. The table provides the success rate across various numbers of consecutive successful sub-tasks (1, 2, 3, 4, and 5). One method, MDT (Multi-modal Diffusion Transformer), is specifically noted as using version 9 of its GitHub repository. Another method, GR-MG, is also included. The table aims to isolate the impact of the action design choices on the model’s performance and generalization ability without the influence of pretraining.
read the caption
Table 9: More action designs w/o pretraining on Calvin (ABC→→\rightarrow→D). MDT is from issue 9 of its GitHub repo and GR-MG.
| # Steps | 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
| All | 61.6% | 60.8 % | 60.6 % | 60.0 % | 58.0 % |
🔼 This table presents the results of an ablation study investigating the impact of varying the number of execution steps on the performance of the Dita model within the ManiSkill2 benchmark. It shows how the model’s success rate changes as the number of steps used for action prediction increases. The results are likely presented as a percentage of successful task completions for each task family in ManiSkill2, providing insights into the model’s ability to generalize across different manipulation tasks and the optimal balance between prediction accuracy and computational cost. The table helps determine the ideal number of execution steps for efficient and effective task completion.
read the caption
Table 10: The effect of the number of execution steps (# Steps) on ManiSkill2.
| Shuffle Buffer Size | cokecan | |
|---|---|---|
| match | variant | |
| 128000 | 71.2% | 73.6% |
| 256000 | 83.7% | 85.5% |
🔼 This table presents the results of an ablation study investigating the impact of the shuffle buffer size in the TensorFlow datasets on the performance of the Dita model. The study specifically focuses on the SimplerEnv benchmark, using both the ‘match’ and ‘variant’ configurations of the Google Robot task from the RT-1 dataset [8]. The table shows how varying the shuffle buffer size affects the success rate of the Dita model across different tasks within SimplerEnv, offering insights into the model’s sensitivity to this hyperparameter.
read the caption
Table 11: Ablation study of shuffle buffer size on SimplerEnv (both math and variant results of Google Robot [8]).
Full paper#