Do Finetti: On Causal Effects for Exchangeable Data

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with non-i.i.d data. It introduces a novel framework for causal effect estimation in exchangeable data, addressing a significant gap in current causal inference methods. The Do-Finetti algorithm, developed here, enables simultaneous causal discovery and effect estimation, which significantly advances research in multi-environment data analysis. This has implications for many fields.

Visual Insights

#

This figure illustrates the differences in causal effects between independent and identically distributed (i.i.d.) processes and independent causal mechanism (ICM) generative processes. It highlights how conditioning on other observations impacts the interventional effect differently in these two scenarios. The i.i.d. case shows independence between observations, while the ICM generative process demonstrates dependence due to shared latent variables.

In-depth insights

#

Causal Exchangeability

#

Causal exchangeability explores the intersection of causality and exchangeability, aiming to understand causal relationships within data where observations are not independent and identically distributed (i.i.d.). Traditional causal inference methods often assume i.i.d. data, but many real-world datasets exhibit exchangeability, where the order of observations doesn’t affect the joint distribution. This framework investigates how causal mechanisms operate within such exchangeable structures, potentially revealing unique causal insights not accessible with standard i.i.d. methods. A key challenge is defining and identifying interventions in this context, where the traditional do-calculus might not directly apply. This necessitates developing new tools for causal identification and effect estimation that account for the dependencies inherent in exchangeable data, leading to novel approaches for causal discovery and inference within non-i.i.d. settings. The central question is how the assumption of independent causal mechanisms, combined with exchangeability, allows for the identification of causal effects.

Do-Finetti Algorithm

#

The heading ‘Do-Finetti Algorithm’ suggests a novel approach to causal inference, likely leveraging the principles of de Finetti’s theorem within an exchangeable data framework. This implies that the algorithm operates on data where observations are not independent and identically distributed (i.i.d.), a common assumption violated in many real-world scenarios. The algorithm likely combines concepts from causal graphical models (e.g., directed acyclic graphs) with the de Finetti representation of exchangeable data to simultaneously perform causal structure learning and causal effect estimation. This is a significant departure from traditional methods that usually require separate steps, and often assume i.i.d. data. A key aspect would be the ability to handle dependencies between data points stemming from the exchangeable structure; the approach likely involves techniques to account for these dependencies during both structure discovery and effect estimation. The ‘Do-Finetti’ aspect suggests a connection to the ‘do-calculus’, a framework for causal inference that deals with interventions. This hints at the algorithm’s capability to estimate causal effects under interventions, directly from the exchangeable data. The algorithm’s efficacy likely depends on the correctness of the underlying assumption of independent causal mechanisms (ICM) within the exchangeable process and would benefit from rigorous empirical validation.

ICM Generative Process

#

The concept of an ICM (Independent Causal Mechanisms) generative process is crucial for understanding causal inference in scenarios beyond the traditional i.i.d. (independent and identically distributed) data assumption. ICM posits that distinct causal mechanisms within a system are independent of one another, meaning that changes in one mechanism do not influence others. This independence is key to identifying and estimating causal effects. An ICM generative process builds upon this foundation, generating data that exhibits exchangeability—the joint distribution remains invariant under permutations of the data points. This exchangeability, combined with the ICM assumption, offers unique opportunities for causal discovery and effect estimation, particularly when dealing with data from multiple environments or with complex dependencies between variables. Unlike traditional methods, which often struggle with non-i.i.d. data, the framework arising from an ICM generative process leverages the richness of exchangeable data to uncover causal relationships that might otherwise be obscured. A key advantage is that it enables unique causal structure identification and allows for the development of algorithms that simultaneously discover causal structure and estimate causal effects. This is especially significant for multi-environment data, where traditional methods often fail to appropriately handle the dependence across different settings.

Multi-Env. Causal Effects

#

The concept of “Multi-Env. Causal Effects” suggests analyzing causal relationships across multiple environments. This approach is crucial because traditional causal inference often assumes identical data distributions across all settings, an unrealistic simplification. By studying causal effects in varied environments, we can identify robust causal relationships that generalize better and understand how environmental factors influence those relationships. This involves developing techniques to handle heterogeneous data distributions from multiple environments. A key challenge is disentangling the genuine causal effects from spurious correlations stemming from environmental differences. Statistical methods focusing on invariant causal mechanisms become vital, allowing us to isolate the true causal structure despite environmental variations. Data integration and causal discovery across multiple environments is necessary to make inferences, potentially involving sophisticated causal modeling techniques. The ability to generalize causal findings from one environment to another based on a shared causal structure is a key goal, enhancing the practical relevance of causal analyses.

Future Research

#

Future research directions stemming from this work could explore several promising avenues. Extending the theoretical framework to encompass more complex data structures beyond exchangeable data, such as those exhibiting temporal dependencies or network effects, would significantly broaden its applicability. Investigating the impact of model misspecification on causal effect estimation within this framework is crucial, as it will help to understand the robustness of results in real-world scenarios where the true generative process is usually unknown. Furthermore, developing more efficient algorithms for causal discovery and effect estimation in high-dimensional settings is essential for practical applications. Finally, exploring connections between this framework and other causal inference approaches, like those based on potential outcomes or graphical models, could reveal new insights and integration opportunities, leading to a more comprehensive and powerful methodology for causal analysis.

More visual insights

#

More on figures

This figure compares how the do operator affects causal inference in two different data generation processes: i.i.d. and ICM generative processes. In the i.i.d. case, fixing the exogenous variables (Ux and Uy) uniquely determines the observed variables (X and Y). However, in the ICM generative process, fixing the causal de Finetti parameters (θ and ψ) only determines the distributions of X and Y, not their specific values. The figure illustrates how the do operator is redefined for ICM generative processes: by setting the intervened variable to a delta distribution and substituting the corresponding value in the other distributions.

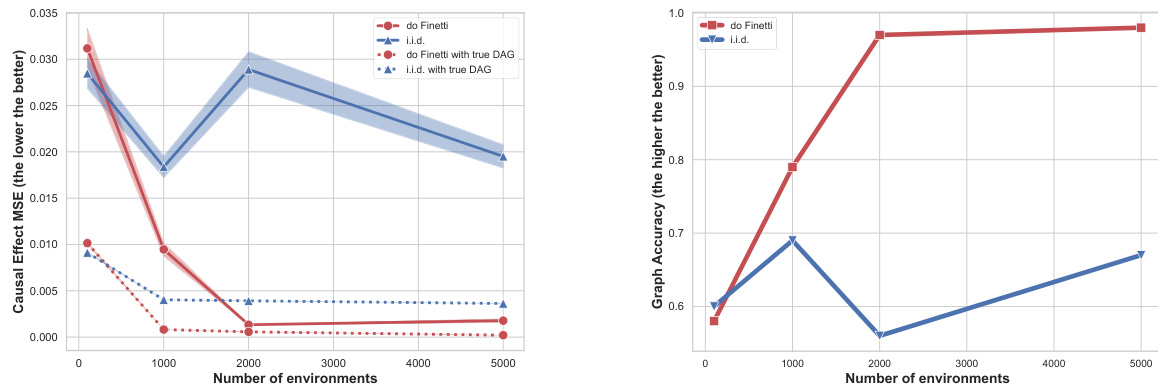
The figure compares the performance of the proposed Do-Finetti method to the standard i.i.d. method in estimating causal effects and identifying the DAG structure in a bivariate setting. The left panel shows the mean squared error (MSE) in causal effect estimation, while the right panel shows the accuracy of DAG identification. The results demonstrate that the Do-Finetti method significantly outperforms the i.i.d. method, especially as the number of environments increases.

Full paper

#