Trading Place for Space: Increasing Location Resolution Reduces Contextual Capacity in Hippocampal Codes

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers studying spatial memory and hippocampal function. It provides a novel geometric framework for analyzing hippocampal place cell activity, offering valuable insights into the capacity of this brain region for storing contextual information. This research opens new avenues for investigating the neural mechanisms underlying spatial navigation and memory, including the impact of place field properties on both spatial precision and contextual capacity.

Visual Insights

#

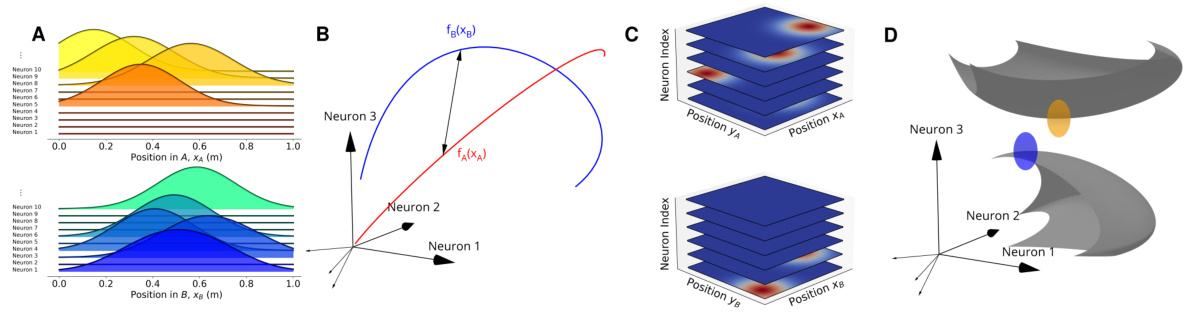
This figure illustrates the concept of place cell remapping in one and two dimensions. Panel A shows how place cell firing fields remap in a one-dimensional environment, while panel C demonstrates remapping in a two-dimensional environment. Panel B depicts the representation of these one-dimensional environments as curves in a high-dimensional neural activity space. The distance between these curves determines the ability to discriminate between different contexts. With added noise, the curves broaden, and a minimum distance is required for discrimination. Panel D shows the same concept for two-dimensional environments, but here the environments are represented as surfaces. In the presence of noise, these surfaces become thicker, and non-overlapping is required for accurate discrimination.

In-depth insights

#

Hippocampal Capacity

#

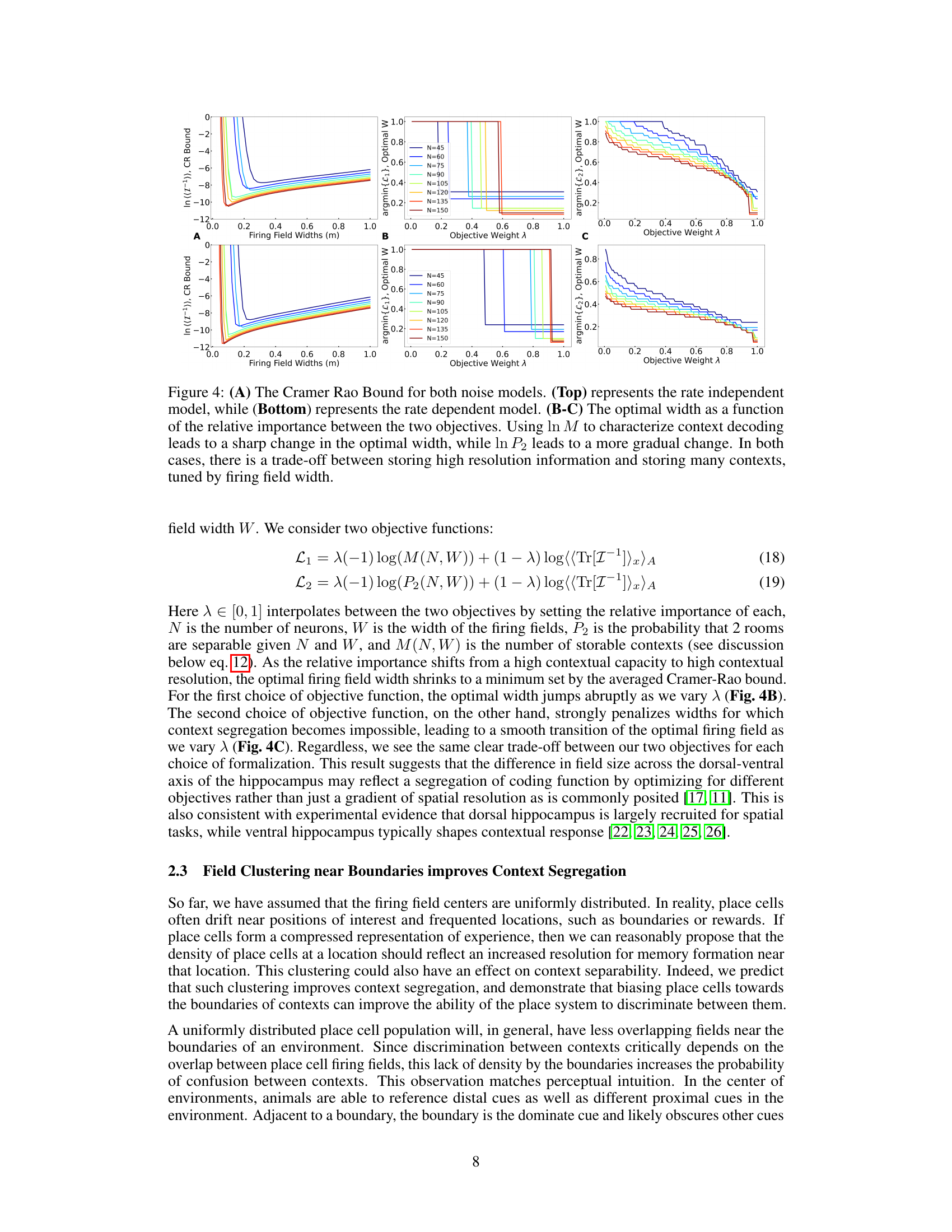
The concept of “Hippocampal Capacity” refers to the brain’s ability to store and retrieve contextual information, particularly spatial memories. The research explores the limits of this capacity, proposing a geometric model. The hippocampus’s capacity scales exponentially with the number of place cells, indicating a remarkably efficient storage system. However, a critical trade-off emerges between the resolution of spatial encoding and the number of contexts storable. Higher resolution (smaller place fields) sacrifices contextual capacity, while lower resolution (larger fields) improves it but reduces spatial precision. This trade-off is naturally tuned by the size of place cell firing fields and could potentially explain the observed variation of place field size along the hippocampal axis. Clustering of place cells near boundaries further enhances the capacity, suggesting that efficient encoding strategies are implemented by the brain to maximize storage efficiency.

Place Field Effects

#

Place field properties, specifically their size and distribution, profoundly impact hippocampal coding. Larger place fields facilitate the encoding of more distinct contexts by increasing the distance between the neural representations of different environments. However, this benefit comes at the cost of reduced spatial resolution, making it harder to precisely decode location. Conversely, smaller place fields enhance spatial precision but limit the number of contexts that can be reliably discriminated. This trade-off, tuned by place field width, suggests a functional specialization along the dorsal-ventral axis of the hippocampus, potentially explaining the observed gradient in field size. Furthermore, the strategic clustering of place fields near boundaries enhances context segregation, potentially enhancing overall coding capacity. This model highlights a balance between spatial precision and contextual discrimination, offering a valuable perspective on hippocampal function.

Contextual Encoding

#

Contextual encoding in hippocampal place cell systems is a fascinating area of neuroscience. The paper highlights the crucial role of place cell remapping in representing different contexts. Rather than simply encoding spatial location, place cells exhibit flexible firing patterns that adapt to changes in environmental cues. This remapping mechanism allows the brain to disentangle spatial information across multiple contexts, preventing interference and enabling efficient memory formation. A geometric framework is proposed for understanding this contextual capacity, analyzing the distances between representations of different environments in neural activity space. This geometric perspective reveals a fundamental trade-off: high spatial resolution encoding comes at the cost of reduced contextual capacity, suggesting a potential computational constraint. Furthermore, the paper investigates how place field properties, particularly width, and spatial distribution, including potential clustering near boundaries, influence the ability of place cells to store multiple contexts, offering a potential mechanism for optimized information processing.

Geometric Approach

#

The research paper utilizes a geometric approach to model hippocampal place cell activity, viewing population activity as a high-dimensional space where different contexts embed as manifolds. This approach offers a novel perspective by focusing on the distances between representations of different environments in this activity space. By considering the geometry of these manifolds and the effects of noise, the authors calculate the contextual capacity of the system and identify a trade-off between the resolution of position encoding and the number of contexts that can be stored. This framework allows for the incorporation of known place cell firing field statistics and different noise models to quantitatively assess how changes to place cell properties affect contextual capacity. The use of geometric concepts, such as manifold distances and ellipsoid intersections, provides a powerful tool for analyzing the hippocampal code and interpreting experimental data on place cell remapping. The geometric approach helps quantify the relationship between place field properties and contextual capacity, offering a quantitative framework for understanding the limits of hippocampal context storage. The mathematical rigor of the approach provides a solid foundation for future research investigating other cell types and abstract spaces.

Future Directions

#

Future research could explore how the geometric framework presented in this paper can be extended to incorporate other hippocampal cell types, such as grid cells and border cells, to build a more holistic understanding of spatial coding and memory. Investigating how remapping interacts with these other cell types and how it affects the overall contextual capacity of the system would provide critical insights into the workings of the hippocampus. Another valuable direction would be to investigate how network effects and the architecture of the hippocampus shape its contextual capacity and how this relates to the geometric model. The model’s assumptions, such as the nature of noise and the independence of neuron firing, could be relaxed to better align with empirical observations. Finally, exploring how clustering of place cells near boundaries could be optimized to improve context segregation in larger environments or more complex tasks is a promising area for further research. These extensions would provide deeper insights into the hippocampus’s remarkable ability to represent and navigate complex environments.

More visual insights

#

More on figures

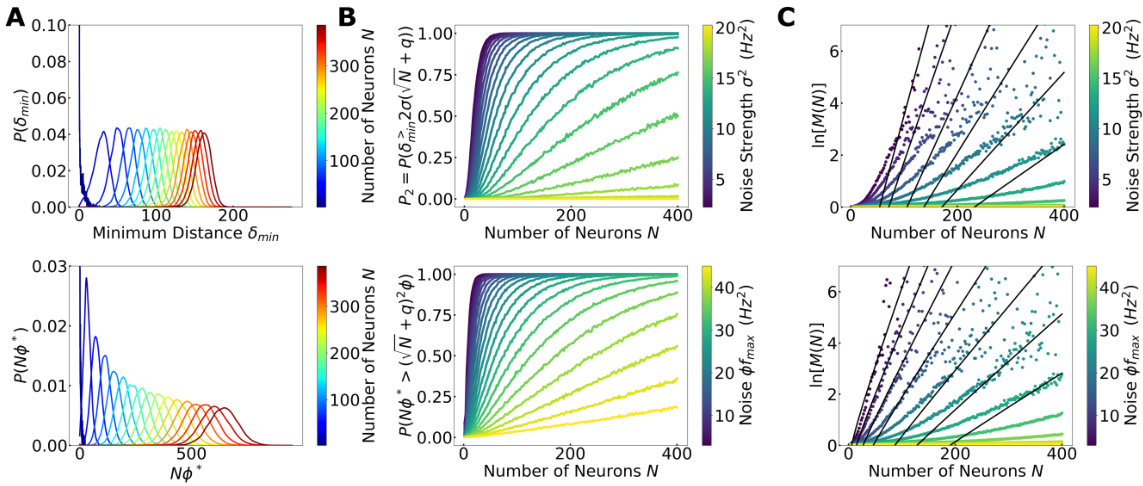
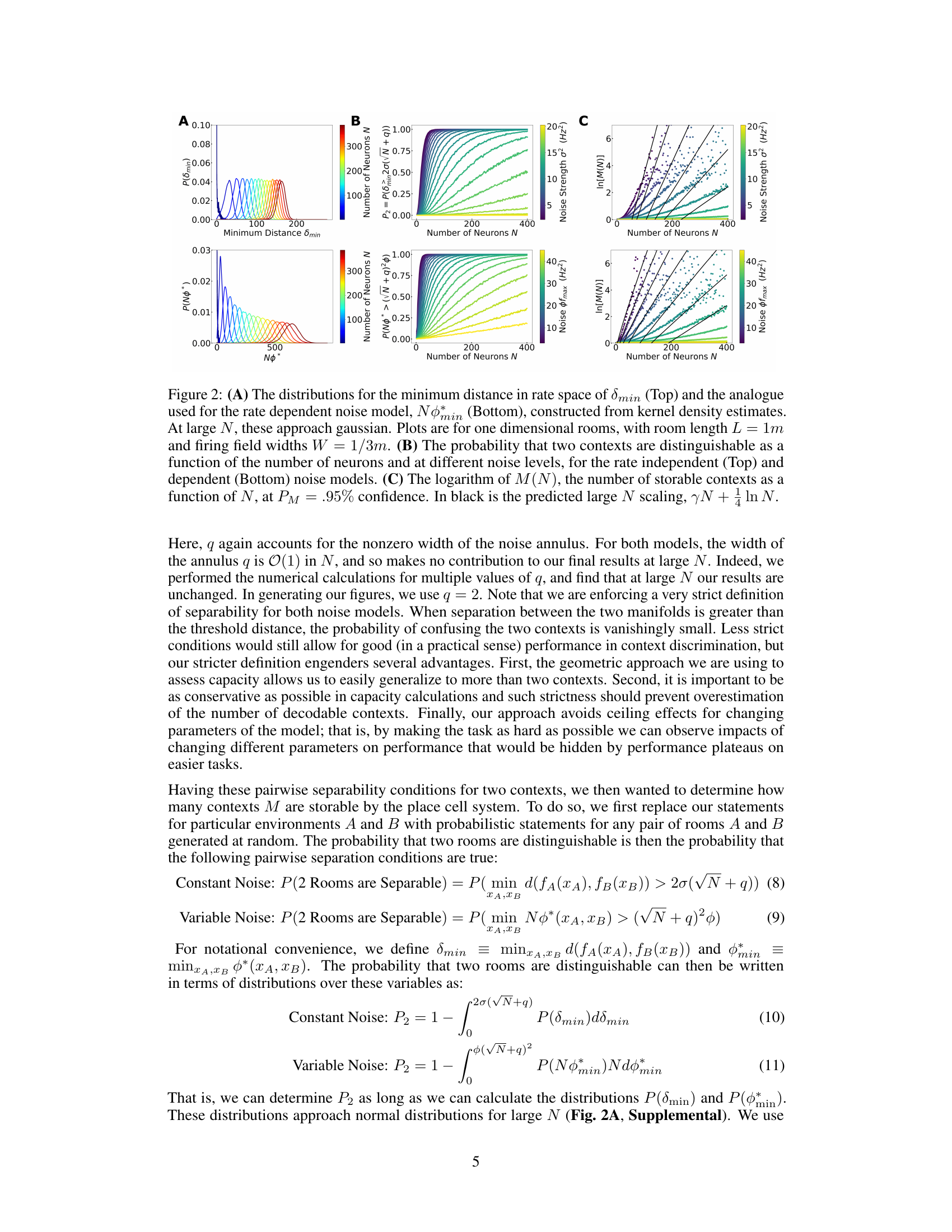
This figure shows the results of the simulations performed in the paper. Panel A shows the distributions of the minimum distances in rate space for both the constant and rate-dependent noise models. Panel B displays the probability that two contexts are distinguishable given different noise levels and numbers of neurons. Finally, panel C depicts the relationship between the number of storable contexts, the number of neurons, and different noise levels. The black line in panel C is a prediction made based on the theoretical analysis.

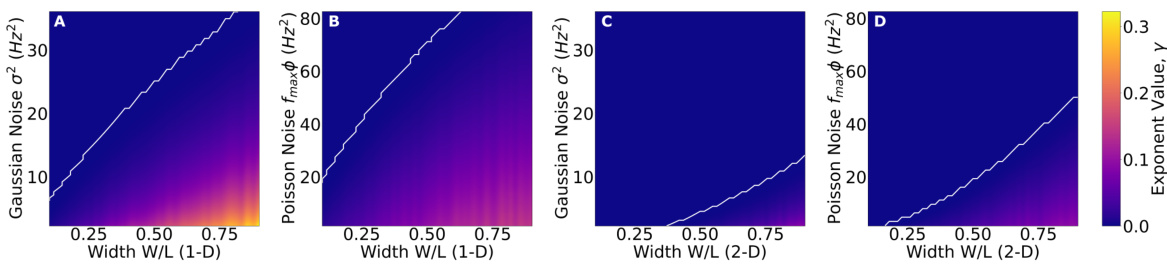
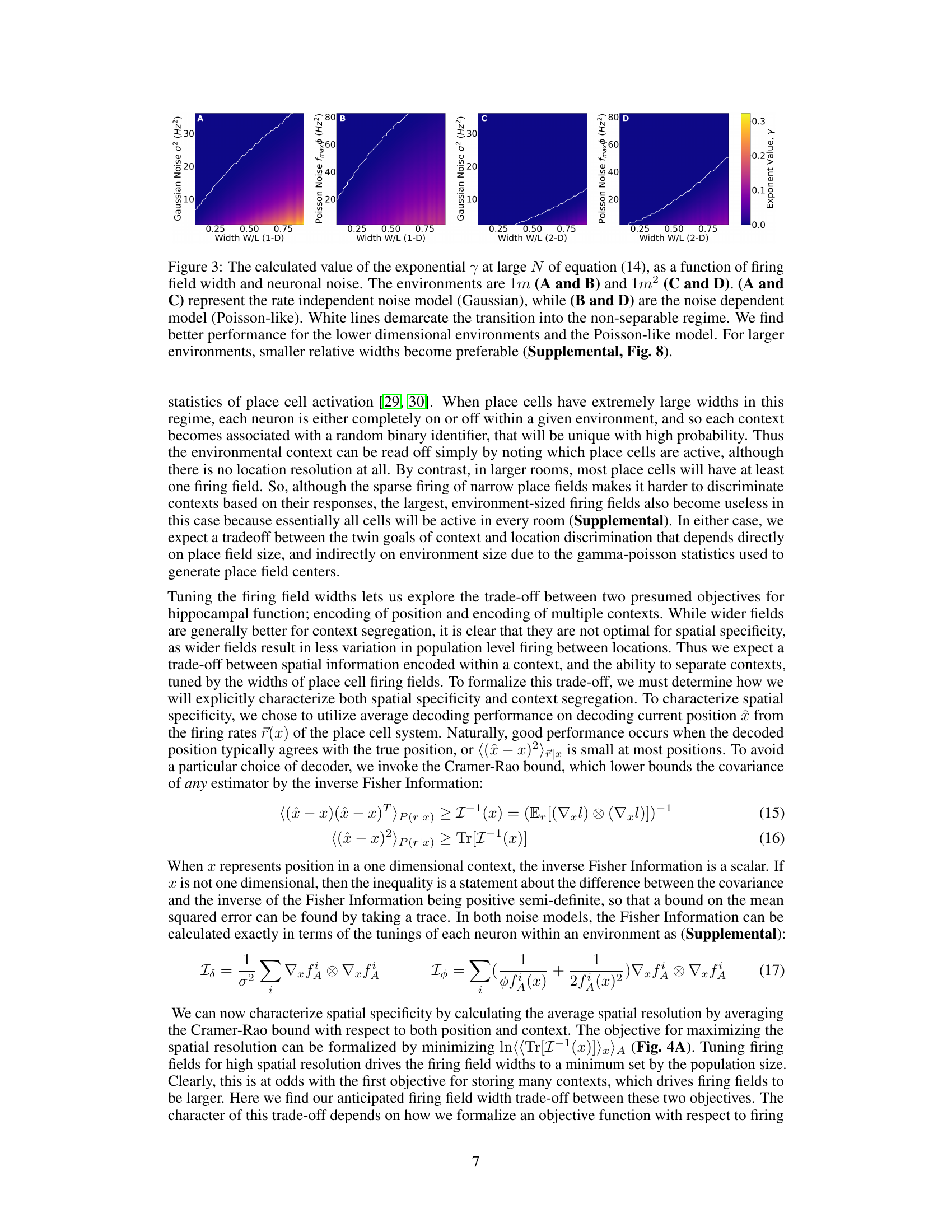
This figure shows the value of the exponential γ (which determines how the number of storable contexts scales with the number of neurons) as a function of firing field width and noise level. It demonstrates that the optimal firing field width depends on the environment dimensionality (1D vs 2D) and the type of noise model (Gaussian vs. Poisson-like). The white lines show when the system can no longer distinguish between contexts. The Poisson noise model is more robust to noise, and narrower relative widths are preferable in larger environments.

This figure shows the value of the exponential y (related to the capacity of the hippocampal place cell system) as a function of firing field width and noise level. The results are shown for both Gaussian (rate-independent) and Poisson-like (rate-dependent) noise models in both one-dimensional (1m) and two-dimensional (1m²) environments. The plots reveal a trade-off between context separation and spatial resolution tuned by the firing field width. The Poisson-like model is generally more robust to noise. White lines indicate the non-separable regime where context discrimination is no longer reliable.

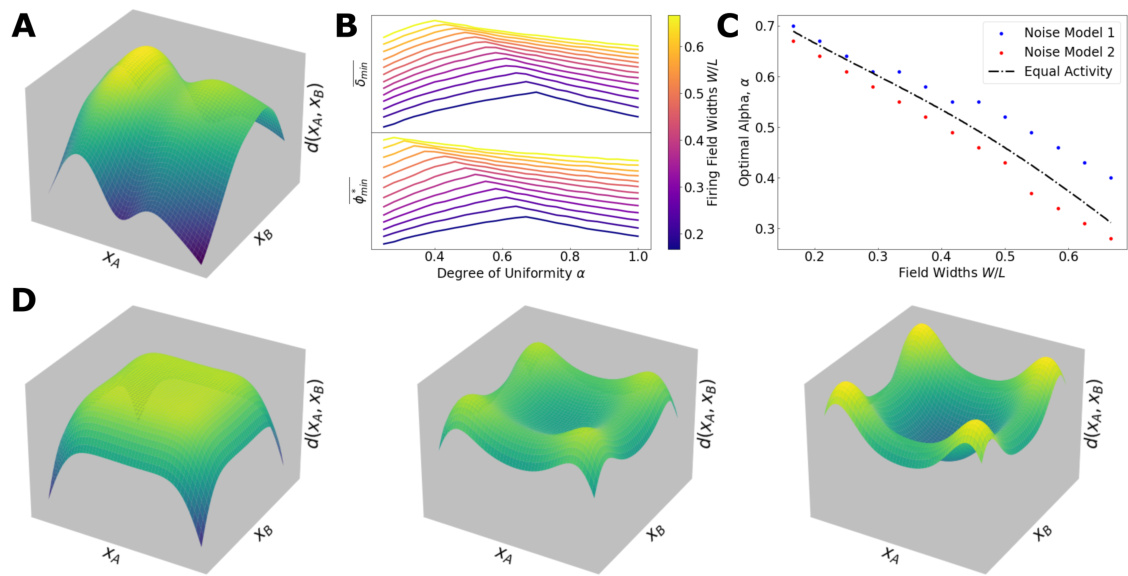
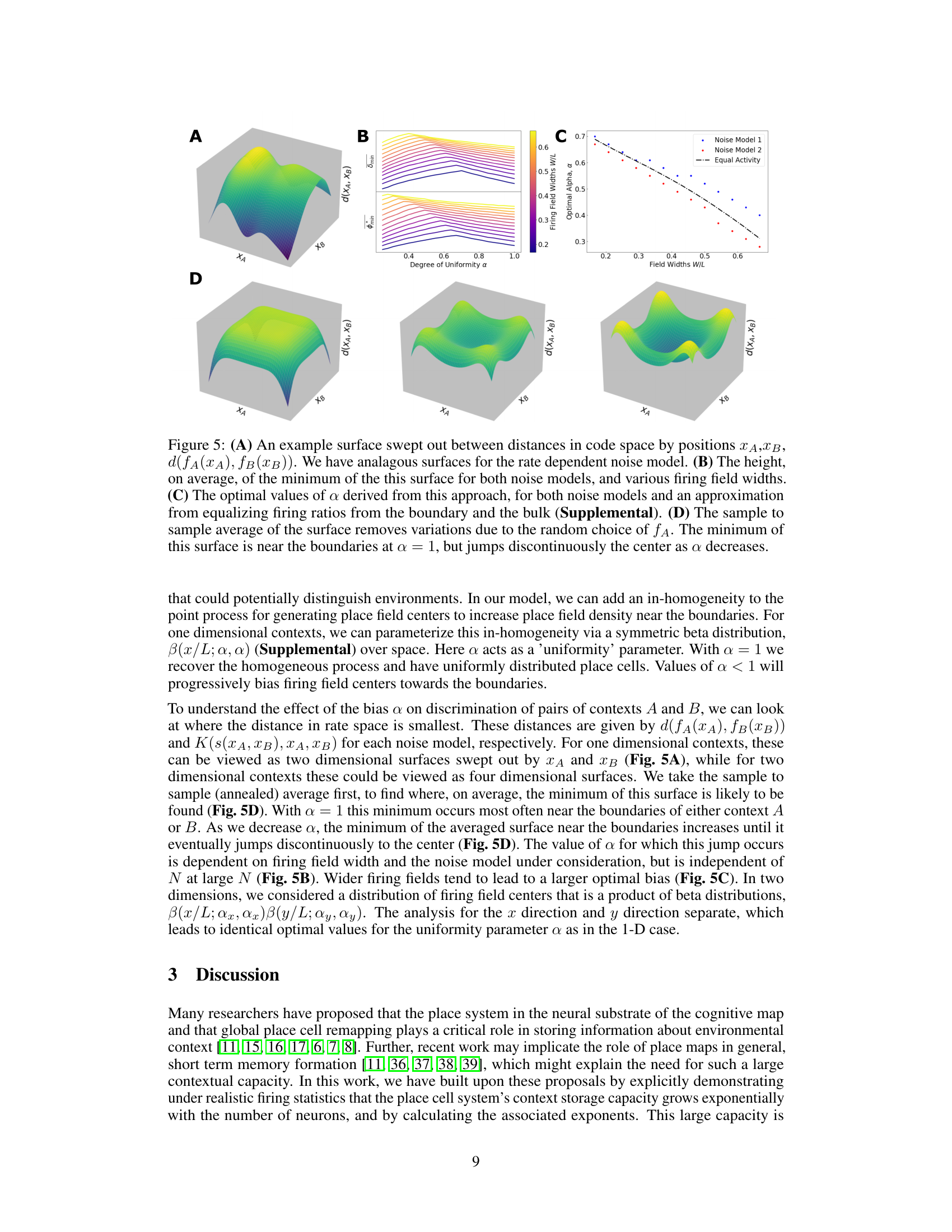
Figure 5 shows the effect of inhomogeneous place cell distribution on context separation. Panel A displays the surface of minimum distances in neural activity space between two contexts as a function of the positions within each context. Panel B shows the average minimum distance for different firing field widths and place cell distribution biases. Panel C shows the optimal bias for different firing field widths. Panel D shows that the average minimum distance is minimum near the boundary when the bias parameter is 1.

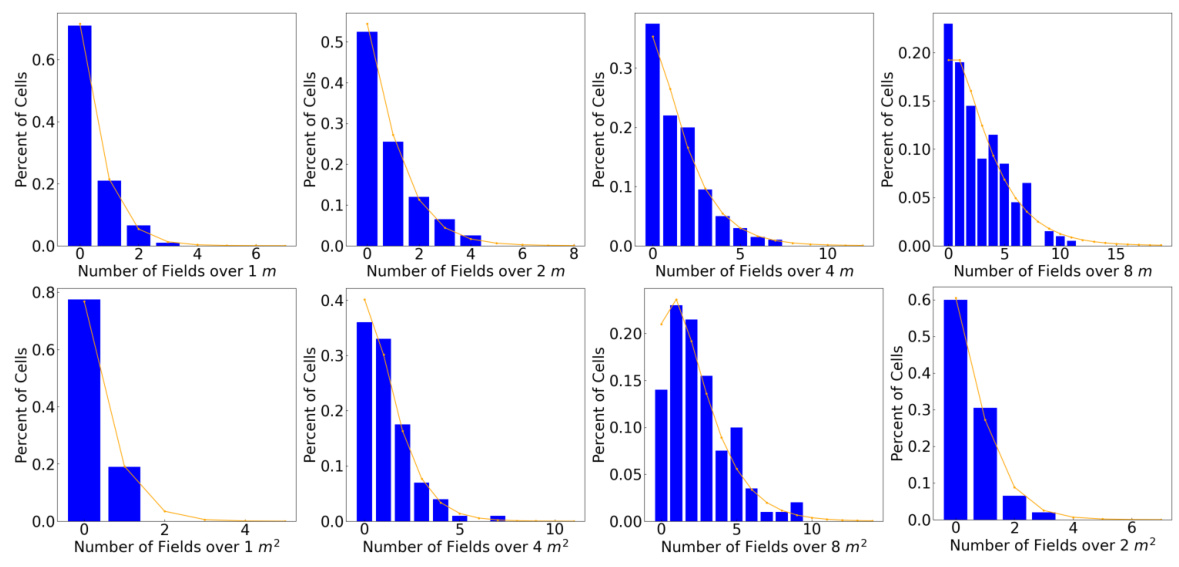
This figure shows the distributions of the number of firing fields per neuron, as determined by the gamma-Poisson distribution used in the simulations. The top row displays these distributions for one-dimensional environments of varying lengths (1m to 8m), while the bottom row shows the distributions for two-dimensional environments (1m² to 8m²). The key observation is that as the size of the environment increases, a larger number of neurons become active and contribute to the representation.

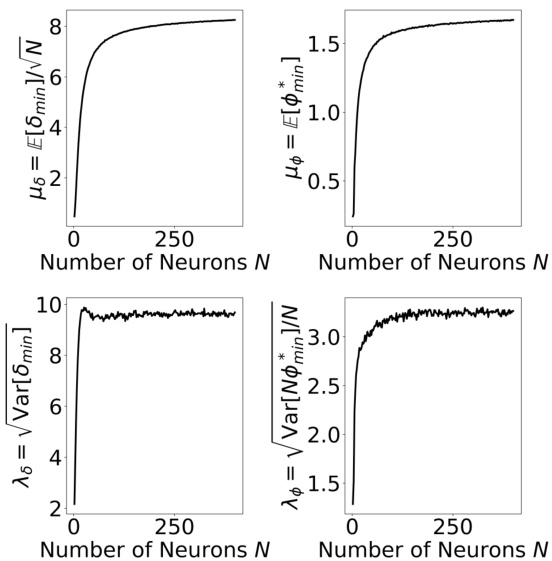
This figure shows the numerical results supporting the theoretical prediction that the constants μδ, λδ, μφ, and λφ, related to the mean and variance of the minimum distances in rate space for both Gaussian and Poisson-like noise models, remain independent of the number of neurons (N) when N is large. The plots show that the values of these parameters converge as N increases, demonstrating that the scaling behavior of the minimum distances is well-approximated by the theoretical model in the large N limit. This supports the analytical derivations made in the paper.

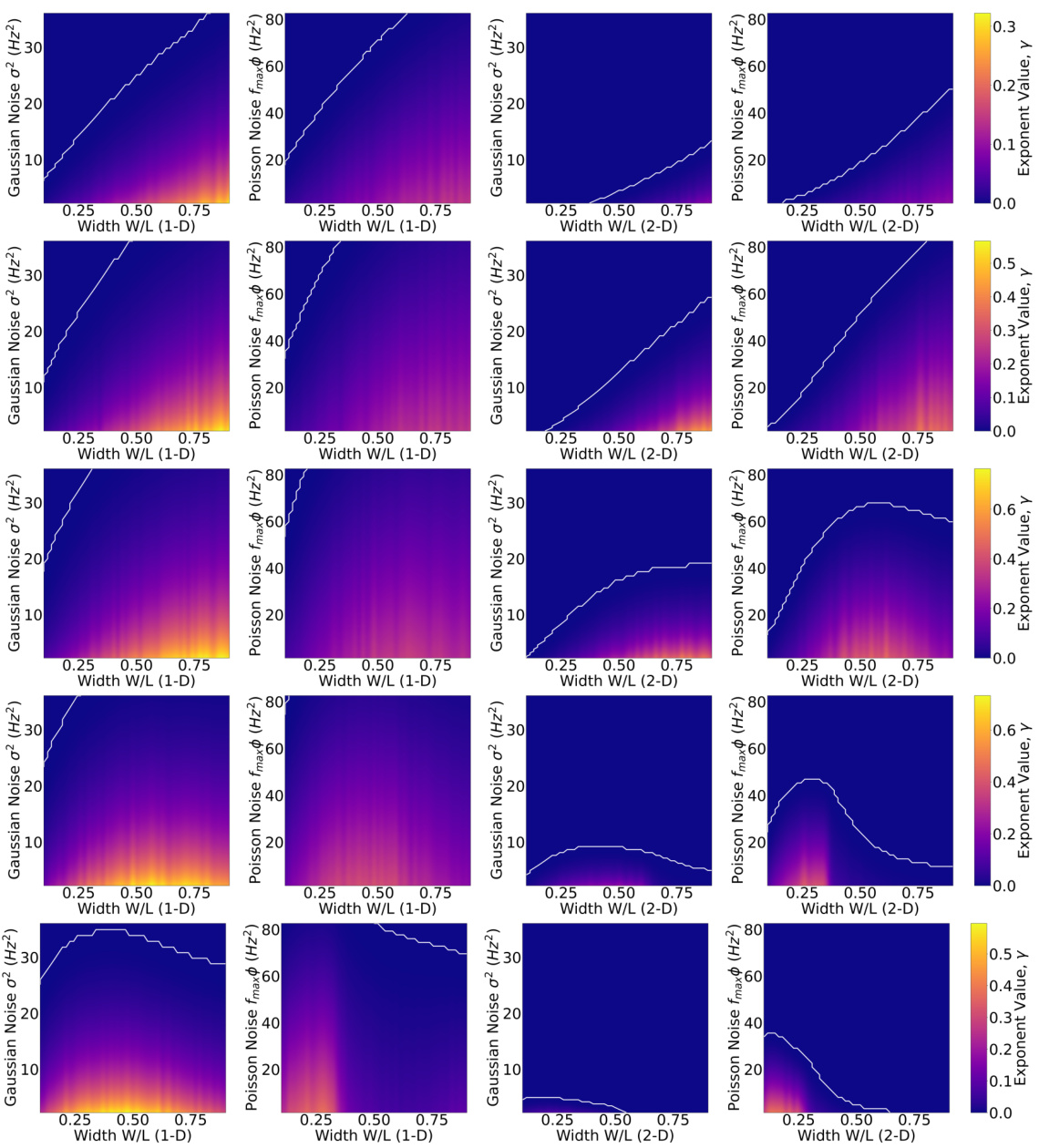
This figure shows the calculated value of the exponential y (from equation 14 in the paper) at large N, which represents the exponential growth of the number of storable contexts with the number of neurons, plotted as a function of firing field width and neuronal noise. The results are shown for both Gaussian (rate-independent) and Poisson-like (rate-dependent) noise models, and for both one-dimensional (1m) and two-dimensional (1m²) environments of varying sizes. The white lines in each subplot indicate the transition to a regime where context separation is no longer possible. Overall, the figure demonstrates a trade-off between firing field width and contextual capacity, influenced by the type of noise and the dimensionality of the environment.

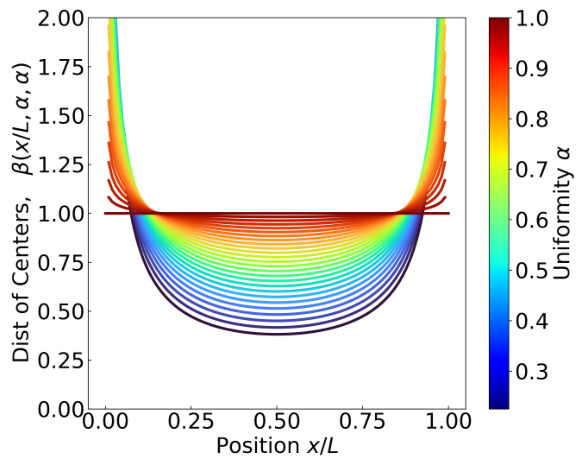
This figure shows beta distributions used to bias the placement of place cell centers towards the boundaries of the environment. The parameter ‘a’ controls the degree of uniformity; when a=1, the distribution is uniform. As ‘a’ decreases, the distribution becomes increasingly concentrated near the boundaries. The plot visualizes this by showing how the probability density changes as a function of position (x/L) across different values of ‘a’.

Full paper

#