↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Many studies use Mendelian Randomization (MR) to infer causal relationships from observational data. However, traditional MR methods often assume a one-directional relationship and struggle with invalid instrumental variables (IVs). This research addresses these limitations by focusing on bi-directional MR, where causal effects flow in both directions. The presence of unmeasured confounding and invalid IVs makes accurate causal effect estimation challenging.
This study introduces a novel algorithm, PReBiM, to tackle these issues. PReBiM uses a cluster fusion-like method to identify valid IV sets and subsequently estimates causal effects using a two-stage least squares approach. The paper provides theoretical justification for the algorithm’s correctness and demonstrates its effectiveness through simulations and real-world examples. The findings advance causal inference methods, particularly in scenarios with bi-directional relationships and potential invalid IVs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with observational data and causal inference, particularly in Mendelian Randomization studies. It offers novel solutions for handling bi-directional causal relationships and invalid instruments, common challenges in many real-world applications. The proposed algorithm and theoretical framework provide valuable tools for accurately estimating causal effects, opening up new avenues for research across diverse fields.
Visual Insights#
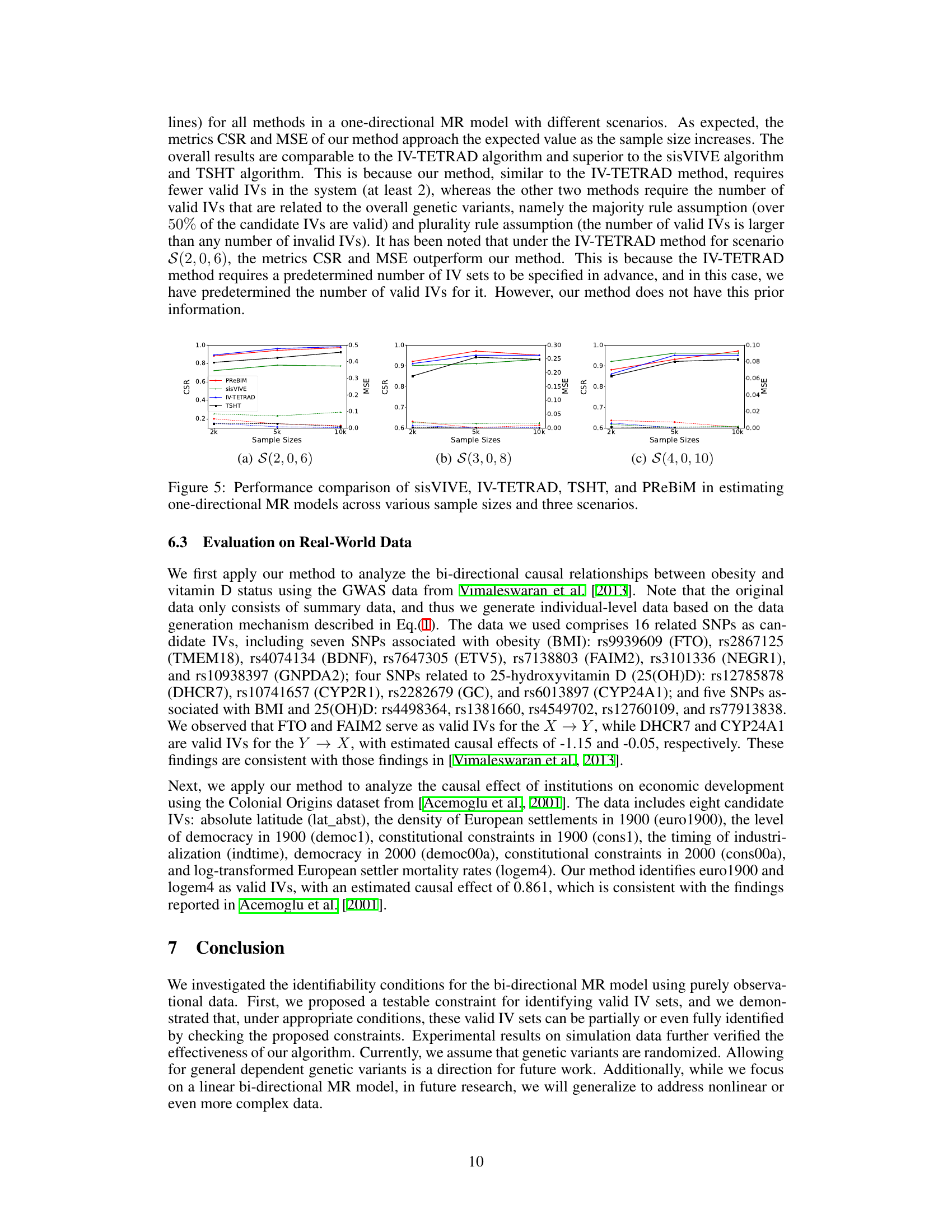
This figure is a graphical illustration of a valid instrumental variable (IV) model in Mendelian Randomization (MR). It shows the relationship between SNPs (G), a risk factor (X, e.g., obesity), an outcome (Y, e.g., Vitamin D status), and unmeasured confounders (U, e.g., lifestyle factors). The solid arrows represent direct causal relationships. The dashed lines indicate the absence of a direct causal relationship. The three assumptions for a valid IV (Relevance, Exclusion Restriction, and Randomness) are represented by A1, A2, and A3, respectively, and the violations of A1, A2, and A3 are marked with a red ‘x’. The assumption A1 is that the genetic variants (G) are associated with the exposure (X). The assumption A2 is that the genetic variants (G) do not have a direct pathway to the outcome (Y). The assumption A3 is that the genetic variants (G) are uncorrelated with unmeasured confounders (U). The figure demonstrates how a valid instrument (G) is used to reliably estimate the causal effect of X on Y, while accounting for unmeasured confounding.
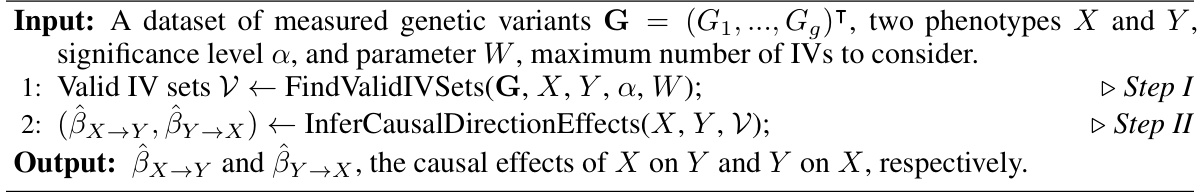
This table presents the results of six different methods used to estimate causal effects in bi-directional Mendelian Randomization (MR) models. The methods are compared across three scenarios with varying numbers of valid and invalid instrumental variables, and across different sample sizes (2k, 5k, and 10k). The metrics used for comparison are the Correct-Selecting Rate (CSR), which measures the proportion of correctly identified valid instrumental variables, and the Mean Squared Error (MSE), which measures the accuracy of the causal effect estimates. The table allows for a quantitative comparison of the methods’ performance under different conditions.
In-depth insights#
Bi-directional MR#
The concept of “Bi-directional Mendelian Randomization (MR)” introduces a significant departure from traditional MR analysis, which typically assumes a unidirectional causal relationship between exposure and outcome. Bi-directional MR acknowledges that in many real-world scenarios, the relationship can be reciprocal, meaning both variables influence each other. This complexity requires more sophisticated approaches to disentangle the causal effects, as standard MR techniques are ill-equipped to handle such feedback loops. The paper addresses the challenge of identifying valid instrumental variables (IVs) in this bi-directional context, where the presence of invalid IVs and unmeasured confounding further complicate the process. A key contribution lies in the identification of conditions for identifiability, enabling the estimation of causal effects despite these complexities. The proposed methodology tackles the issue of selecting valid IVs from observed data, a crucial step towards unbiased effect estimation in bi-directional settings. The algorithm developed, PReBiM, aims to robustly achieve this through a novel cluster fusion approach. Correctness and computational efficiency are theoretically analyzed, showing the potential for effective causal inference in a wider range of applications than allowed by traditional MR.
Invalid IVs#
The concept of ‘invalid instrumental variables’ (IVs) is crucial in Mendelian Randomization (MR) studies. Invalid IVs violate the core assumptions of instrumental variable analysis, leading to biased causal effect estimates. These violations typically stem from horizontal pleiotropy, where genetic variants influence the outcome through pathways other than the exposure of interest. Identifying and handling invalid IVs is challenging, as they can’t be directly observed and various statistical methods exist, each with its own assumptions and limitations. The paper explores this challenge in the context of bi-directional MR, where the treatment and outcome may have a reciprocal causal relationship, further complicating the identification of valid instruments. The presence of unmeasured confounding adds to the complexity, making the identification of true causal effects even more difficult. Strategies for addressing invalid IVs include statistical methods that attempt to account for or remove their influence, such as weighted median estimators or MR-Egger regression, and algorithms aiming to select sets of valid IVs directly from the observed data. However, choosing the most appropriate method depends heavily on the specific characteristics of the data and the underlying assumptions. Therefore, careful consideration of these issues is critical for obtaining reliable causal inferences in MR studies.
Causal Inference#
Causal inference, the process of drawing conclusions about cause-and-effect relationships, is a critical aspect of many scientific disciplines. This paper focuses on causal inference within the context of Mendelian randomization (MR), a powerful method for estimating causal effects from observational data using genetic variants as instrumental variables. The core challenge addressed is the presence of invalid instrumental variables and unmeasured confounding, which can lead to biased causal effect estimates. The authors propose a novel algorithm, PReBiM, which identifies valid IVs and estimates causal effects even under the presence of these complexities. A key contribution is the establishment of necessary and sufficient conditions for the identifiability of causal effects in bi-directional MR models; this addresses a critical limitation of previous methods which predominantly handled only unidirectional relationships. The paper demonstrates the effectiveness of PReBiM through both theoretical analysis and experimental validation, showcasing its ability to reliably estimate causal effects in complex scenarios. Further research could explore extending the approach to handle nonlinear relationships or more complex confounding structures, as well as evaluating performance with more limited sample sizes.
PReBiM Algorithm#
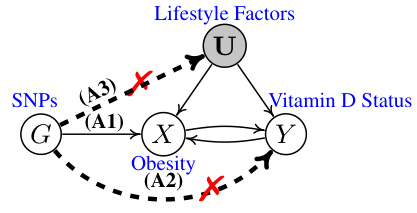
The PReBiM algorithm, a data-driven approach for estimating causal effects in bi-directional Mendelian randomization (MR) models, is presented. It cleverly addresses the challenge of identifying valid instrumental variables (IVs) and determining causal directions in the presence of invalid IVs and unmeasured confounding. The algorithm’s core strength lies in its theoretical foundation, using pseudo-residuals to distinguish valid and invalid IV sets. This is followed by a cluster fusion-like method that efficiently identifies valid IV sets. The algorithm’s correctness is theoretically proven, and its performance is demonstrated through experiments. A key advantage is its ability to handle bi-directional relationships and its relatively low requirement for the number of valid IVs. Further research is needed to explore the algorithm’s performance in complex scenarios and datasets with correlated genetic variants. Although the algorithm is promising, its suitability to scenarios with limited data requires further investigation.
Future Research#
The paper’s conclusion points towards several promising avenues for future research. Extending the model to handle nonlinear relationships is crucial, as many real-world causal effects are not linear. The current model’s reliance on the independence of genetic variants is a limitation; future work should investigate scenarios with dependent genetic variants, making the model more robust to real-world data complexities. Additionally, addressing situations where genetic variants might influence unmeasured confounders or other phenotypes that, in turn, affect the treatment and outcome would significantly enhance the model’s generalizability and practical application. Finally, exploring methods to incorporate prior knowledge or integrate external data sources could lead to improved estimation accuracy and more reliable causal inference. This would be particularly valuable in handling more complex systems with multiple mediators and confounders. Overall, the future research directions highlight the need for increased robustness, sophistication, and applicability of the proposed bi-directional Mendelian randomization model.
More visual insights#
More on figures
This figure illustrates how valid and invalid instrumental variables (IVs) create different constraints in a bi-directional Mendelian Randomization (MR) model. Valid IVs (G1, G3) are those that meet the assumptions of relevance, exclusion restriction, and randomness in relation to the causal effect of X on Y. Invalid IVs (G2, G4, G5) violate the exclusion restriction assumption, having direct pathways to the outcome Y, independent of the exposure X. These different pathways create distinct patterns of correlation, forming the basis for identifying valid IV sets from observational data.
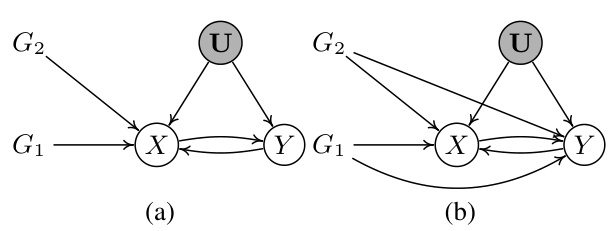
This figure illustrates how valid and invalid instrumental variables (IVs) create different constraints in a bi-directional Mendelian randomization (MR) model. In the figure, G1 and G3 are valid IVs for the causal relationship between X and Y because they meet the three conditions for valid IVs (relevance, exclusion restriction, and randomness). Conversely, G2, G4, and G5 are invalid IVs because they have direct paths to the outcome Y (violating the exclusion restriction). The different sets of valid and invalid IVs lead to distinct correlation patterns that can be used to identify them.
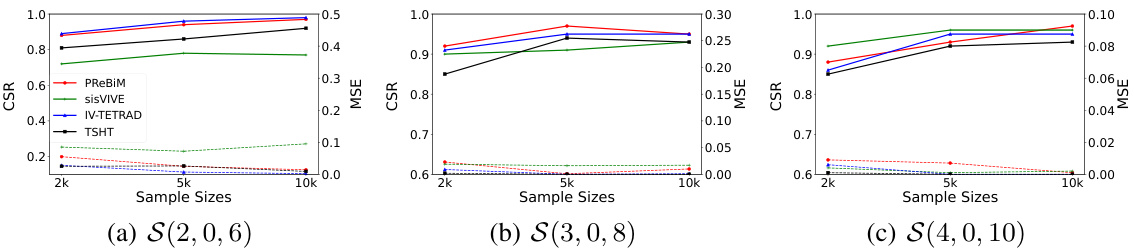
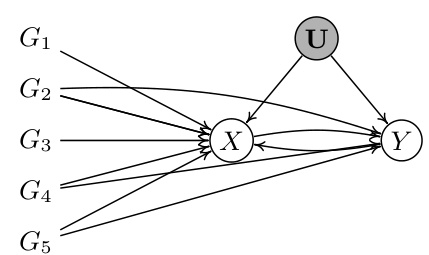
This figure compares the performance of four methods (sisVIVE, IV-TETRAD, TSHT, and PReBiM) in estimating one-directional Mendelian Randomization (MR) models. It shows the Correct-Selecting Rate (CSR) and Mean Squared Error (MSE) for three different scenarios (S(2,0,6), S(3,0,8), and S(4,0,10)) across varying sample sizes (2k, 5k, and 10k). The scenarios likely represent different numbers of valid and invalid instrumental variables. The plot demonstrates how the accuracy (CSR) and error (MSE) of each method change as the sample size increases and varies with the different IV combinations.

This figure illustrates how valid and invalid instrumental variables (IVs) create different constraints in a bi-directional Mendelian randomization (MR) model. It shows two sets of genetic variants (G). The first set, G→Y = (G1, G3), are valid IVs, meaning they meet the criteria of relevance, exclusion restriction, and randomness. The second set, G→Y = (G2, G4, G5), are invalid IVs because they violate the exclusion restriction. These invalid IVs have direct pathways to the outcome variable (Y), confounding the causal effect estimation.
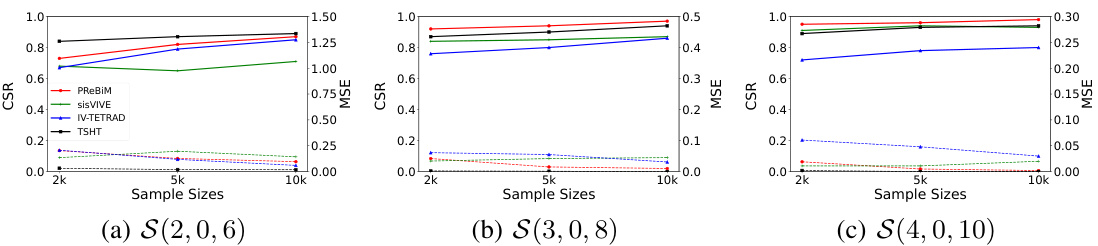
This figure compares the performance of four methods (sisVIVE, IV-TETRAD, TSHT, and PReBiM) in estimating one-directional Mendelian Randomization (MR) models. It shows the Correct-Selecting Rate (CSR) and Mean Squared Error (MSE) for three different scenarios (S(2,0,6), S(3,0,8), S(4,0,10)) across various sample sizes (2k, 5k, 10k). The scenarios likely represent varying numbers of valid and invalid instrumental variables. The figure demonstrates how well each method identifies valid instrumental variables and estimates causal effects under different conditions.
More on tables

This table presents a comparison of six different methods for estimating causal effects in bi-directional Mendelian Randomization (MR) models. It shows the Correct-Selecting Rate (CSR) and Mean Squared Error (MSE) for each method across three different scenarios (varying numbers of valid instrumental variables) and three different sample sizes (2k, 5k, and 10k). The results demonstrate the relative performance of each method in terms of accurately identifying valid instrumental variables and estimating causal effects, highlighting the strengths and weaknesses of each approach in different conditions.

This table compares six methods for estimating causal effects in bi-directional Mendelian Randomization (MR) models with different sample sizes (2k, 5k, 10k) and three scenarios representing different numbers of valid instrumental variables (IVs). The metrics used for comparison are Correct-Selecting Rate (CSR) and Mean Squared Error (MSE). The results show that the proposed PReBiM method generally outperforms the other methods across all scenarios and sample sizes.
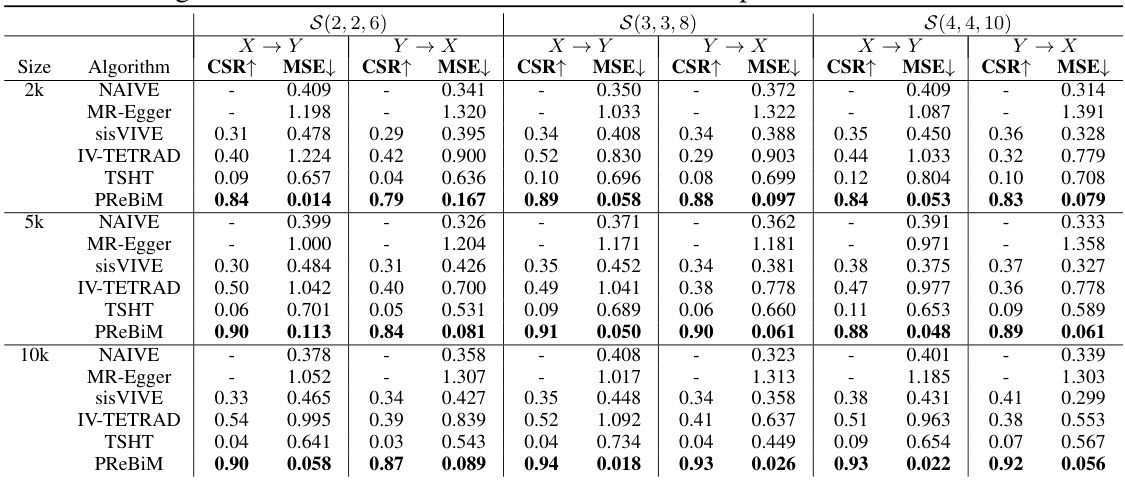
This table compares the performance of six different methods (NAIVE, MR-Egger, sisVIVE, IV-TETRAD, TSHT, and PReBiM) for estimating causal effects in bi-directional Mendelian Randomization (MR) models. The comparison is done across three different scenarios (with varying numbers of valid and invalid instrumental variables) and three different sample sizes (2k, 5k, and 10k). The metrics used for comparison are CSR (Correct-Selecting Rate) and MSE (Mean Squared Error). Higher CSR values and lower MSE values indicate better performance. The results show that PReBiM generally outperforms other methods across all scenarios and sample sizes.

This table presents the results of six methods for estimating causal effects in bi-directional Mendelian Randomization (MR) models with varying sample sizes (2k, 5k, 10k) and three scenarios representing different numbers of valid instrumental variables. The metrics used are CSR (Correct-Selecting Rate), indicating the accuracy of identifying valid IVs, and MSE (Mean Squared Error), showing the accuracy of the estimated causal effects. The table allows for comparison of the performance of the proposed PReBiM method against existing methods like NAIVE, MR-Egger, sisVIVE, IV-TETRAD, and TSHT under different data conditions.
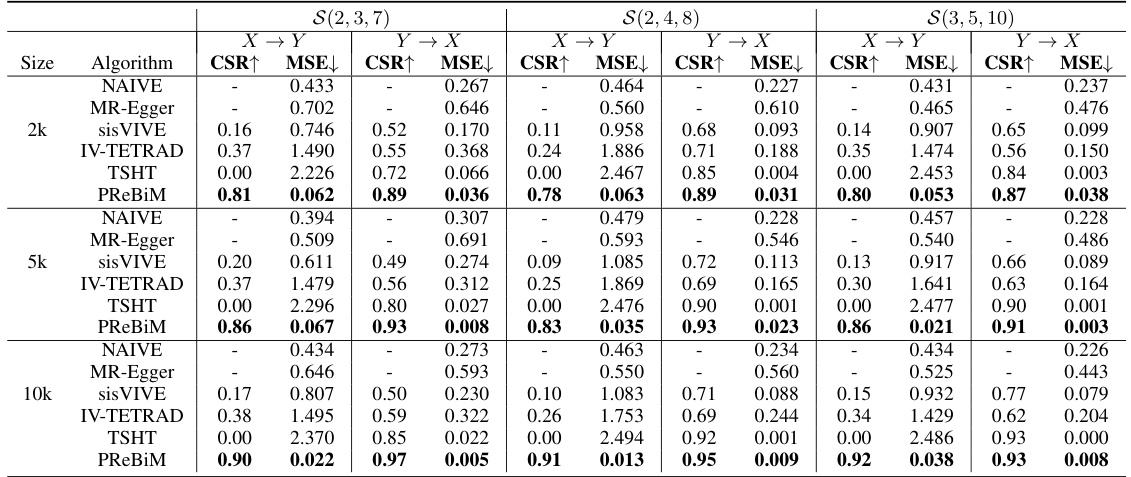
This table presents the results of six methods (NAIVE, MR-Egger, sisVIVE, IV-TETRAD, TSHT, and PReBiM) in estimating causal effects in bi-directional Mendelian randomization (MR) models. It compares their performance across different sample sizes (2k, 5k, 10k) and three scenarios representing varying numbers of valid instrumental variables. The metrics used for comparison are Correct-Selecting Rate (CSR) and Mean Squared Error (MSE). Higher CSR indicates better performance in identifying valid IVs while lower MSE implies more accurate estimation of causal effects. The table allows for assessing the effectiveness of each method under different conditions.
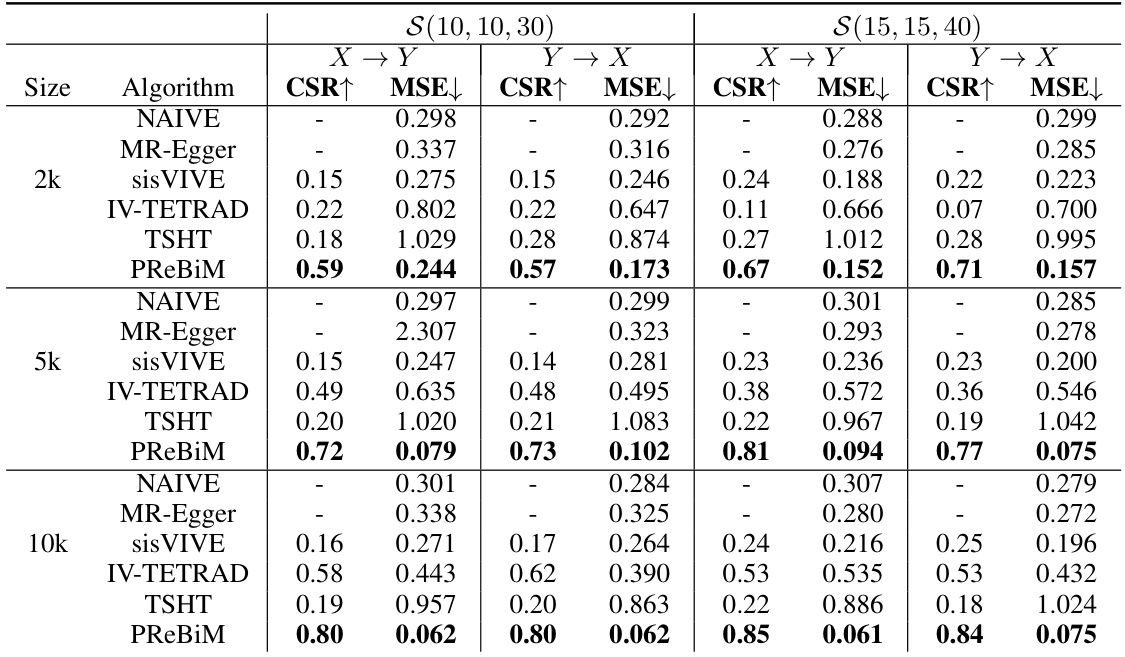
This table presents a comparison of six different methods (NAIVE, MR-Egger, sisVIVE, IV-TETRAD, TSHT, and PReBiM) for estimating causal effects in bi-directional Mendelian Randomization (MR) models. The comparison is made across three different scenarios (varying numbers of valid and invalid instrumental variables) and three different sample sizes (2k, 5k, and 10k). The metrics used for comparison are the Correct-Selecting Rate (CSR) and the Mean Squared Error (MSE). CSR measures the accuracy of identifying valid instrumental variables, while MSE quantifies the accuracy of the causal effect estimates.
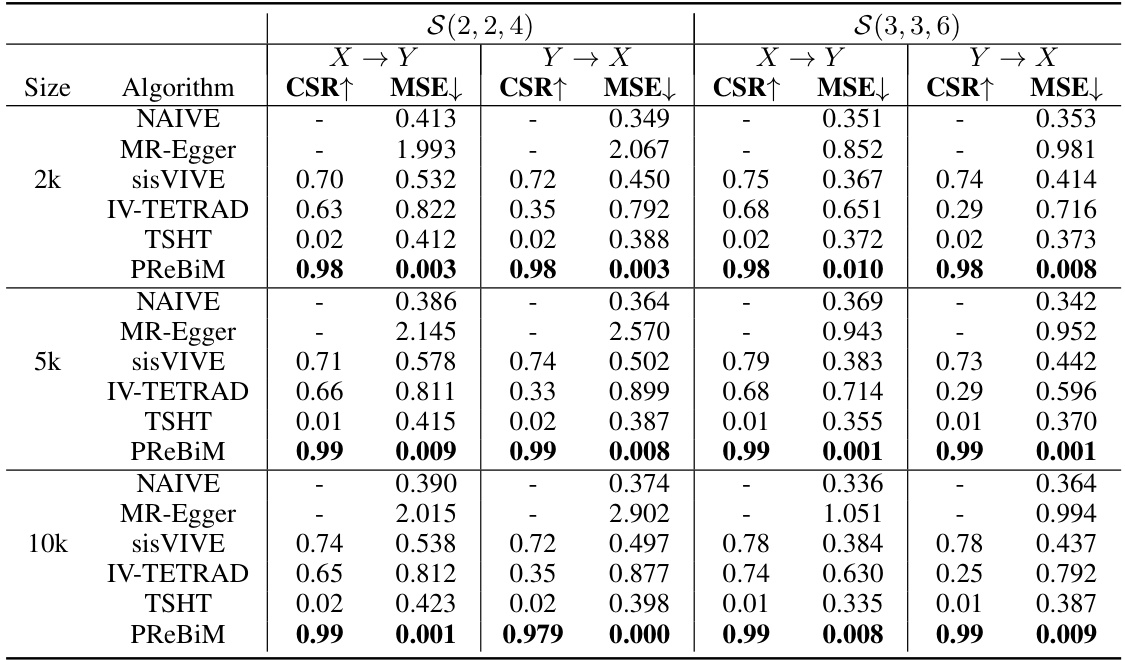
This table presents a performance comparison of six methods (NAIVE, MR-Egger, sisVIVE, IV-TETRAD, TSHT, and PReBiM) for estimating causal effects in bi-directional Mendelian Randomization (MR) models. The comparison is made across three different scenarios with varying numbers of valid and invalid instrumental variables and three different sample sizes (2k, 5k, and 10k). The metrics used for comparison are Correct-Selecting Rate (CSR) and Mean Squared Error (MSE). Higher CSR indicates better performance in identifying valid instrumental variables, while lower MSE shows better accuracy in estimating causal effects.
Full paper#