↗ OpenReview ↗ NeurIPS Proc. ↗ Hugging Face ↗ Chat
TL;DR#
Large Language Models (LLMs) are powerful but resource-intensive. Quantization, reducing the precision of model parameters, is a key technique to make LLMs more efficient. However, activation outliers, unusually large activation values, hinder efficient low-bit quantization, leading to performance degradation. Existing methods struggle to handle these outliers, especially the extreme “Massive Outliers”.
DuQuant tackles this problem by using dual transformations: rotation and permutation. Rotation redistributes outliers across channels, and permutation balances their distribution across blocks. These transformations effectively reduce the impact of outliers, leading to improved low-bit quantization performance. Experiments show that DuQuant outperforms previous approaches across multiple LLMs and tasks, even with only 4-bit quantization, resulting in significant speedups and memory savings during inference. This work significantly advances the state-of-the-art in LLM quantization.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on model compression and efficient deployment of large language models (LLMs). It directly addresses the significant challenge of activation outliers, a major hurdle in achieving high-performance low-bit quantization. By introducing a novel and effective method, DuQuant, the research opens new avenues for developing more efficient and resource-friendly LLMs, particularly relevant in constrained environments. The theoretical analysis and extensive experiments provide a strong foundation for further investigation into outlier mitigation techniques and improving the efficiency of quantized LLMs.
Visual Insights#
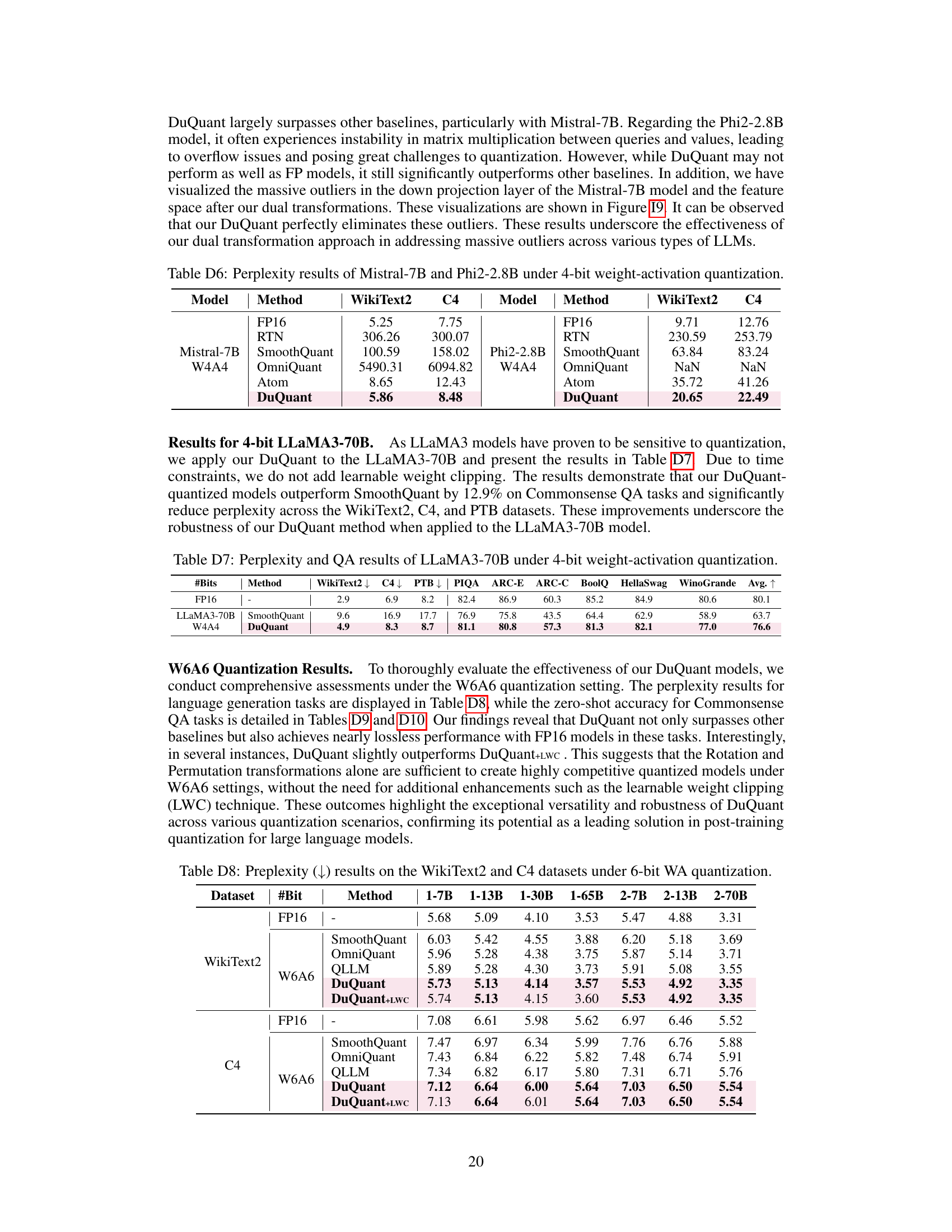
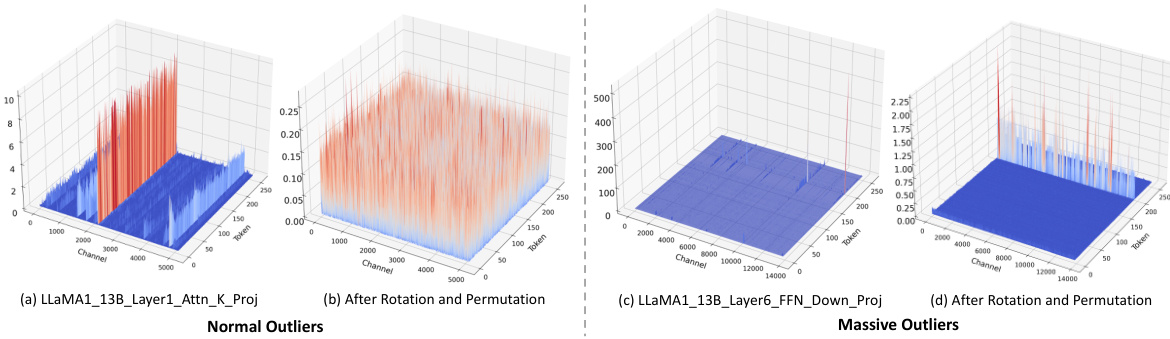
This figure visualizes the different types of outliers found in the LLaMA2-7B model. (a) shows Normal Outliers which have relatively high magnitudes across all tokens. (b) shows Massive Outliers, which are extremely large values found in only a few tokens. (c) and (d) illustrate the application of SmoothQuant on these outliers and how it fails to eliminate the Massive Outliers effectively, even introducing new outliers in the weight matrix.
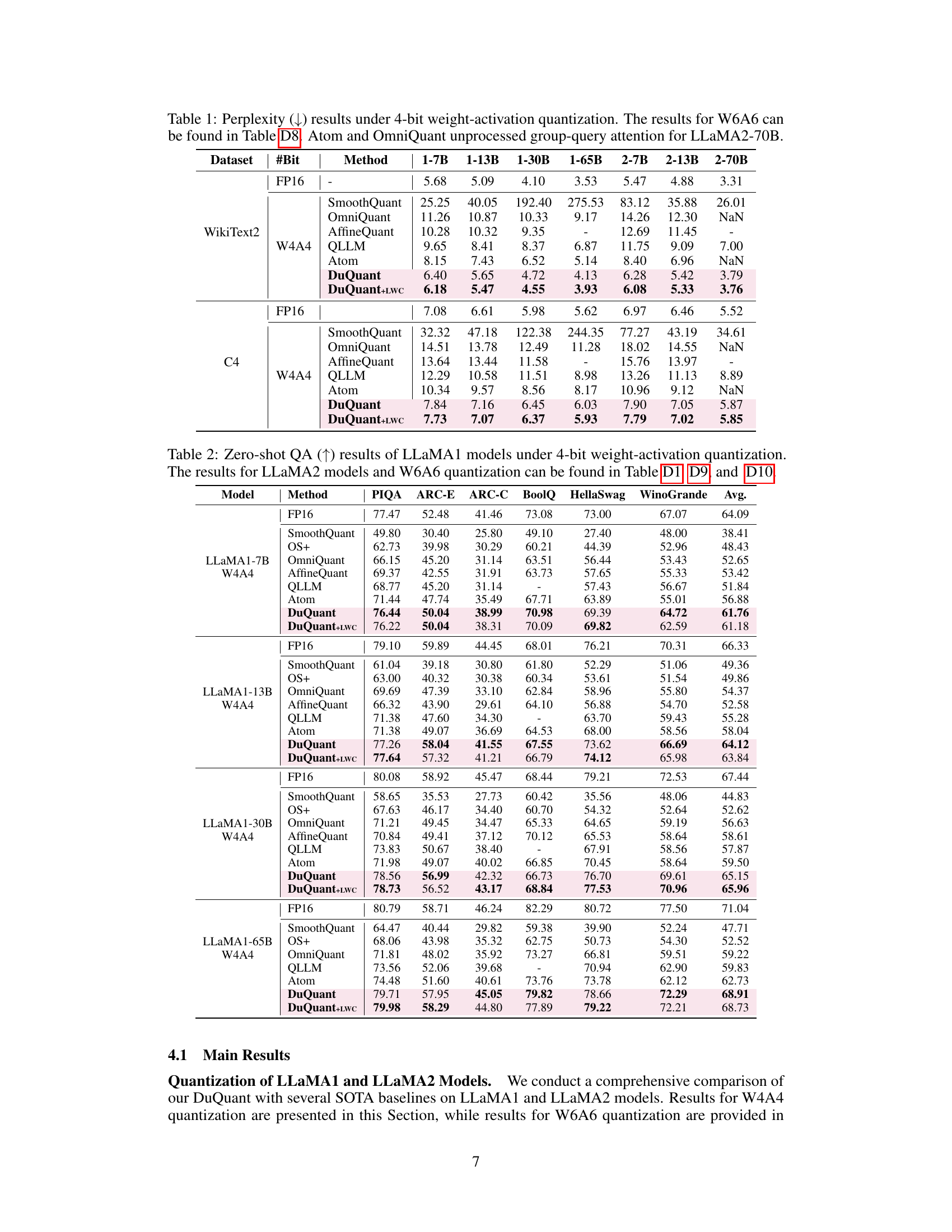
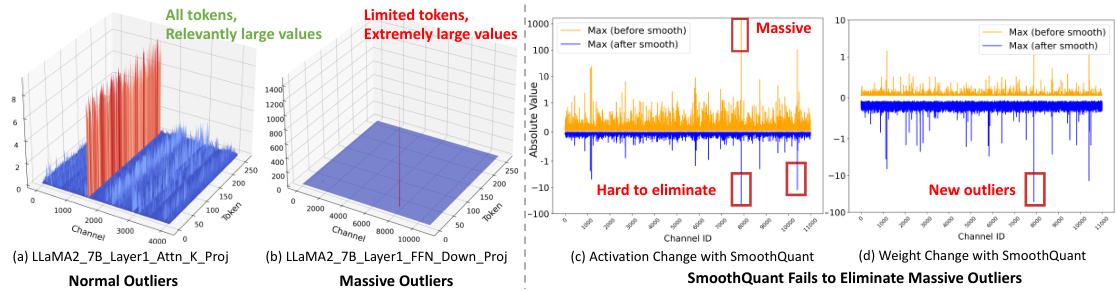
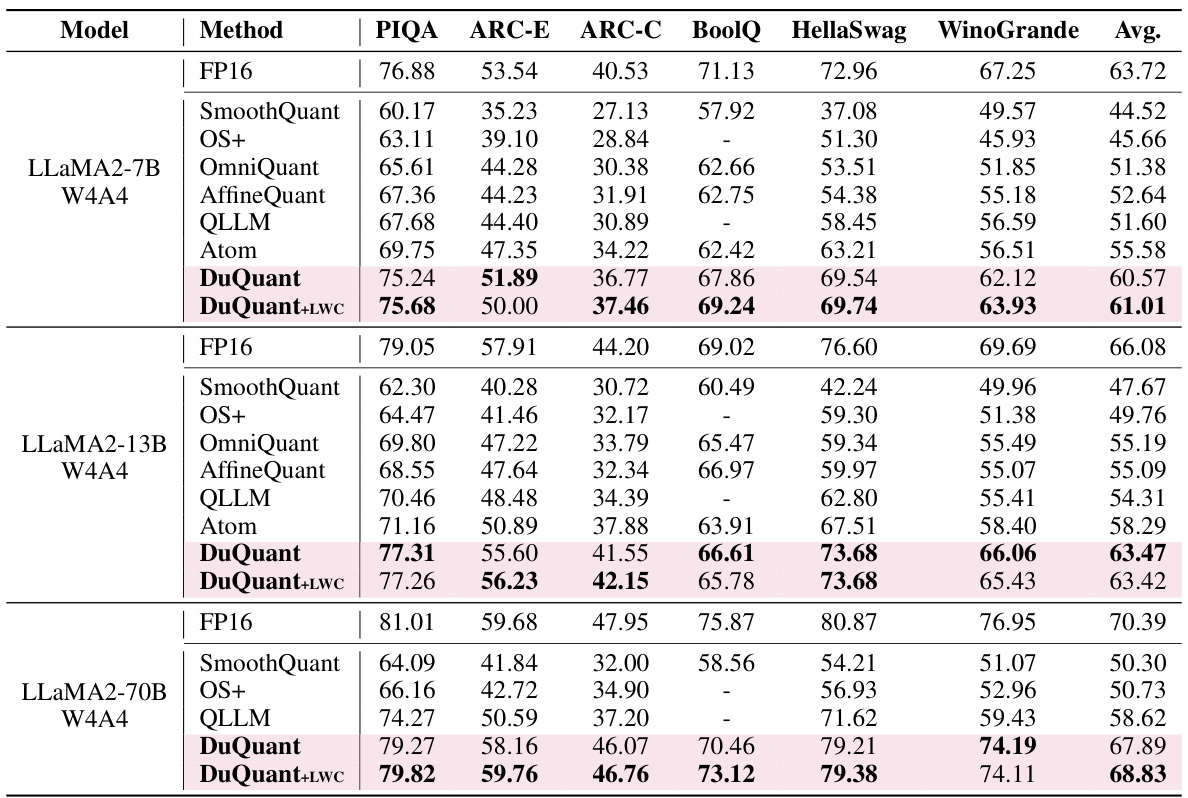
This table presents the perplexity scores achieved by different quantization methods (SmoothQuant, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) on the WikiText2 and C4 datasets using 4-bit weight-activation quantization. Lower perplexity scores indicate better performance. The table compares results across various sizes of LLMs (1-7B to 2-70B parameters). Note that Atom and OmniQuant did not process group-query attention for the LLaMA2-70B model. The results for 6-bit weight-activation quantization (W6A6) are available in Table D8 in the appendix.
In-depth insights#
Outlier Distributions#
Outlier distributions in large language models (LLMs) pose significant challenges for quantization. Traditional methods struggle with outliers exhibiting extremely large magnitudes (Massive Outliers) in addition to the more common Normal Outliers. These outliers disrupt the efficient low-bit representation necessary for model compression and inference speedup. Understanding outlier distributions is crucial because these values disproportionately impact quantization accuracy, leading to a greater loss of precision. Effective strategies must account for the varied nature of these outliers, such as the concentration of Massive Outliers in specific tokens and channels versus the broader presence of Normal Outliers across multiple channels. Strategies that employ rotations and permutations offer a potential solution to manage these outliers by redistributing their influence more evenly across the feature space. This redistribution reduces the impact of outliers and results in better overall model performance, highlighting the importance of addressing the unique characteristics of different outlier types in the pursuit of efficient LLM quantization.
Dual Transformations#
The concept of “Dual Transformations” in the context of quantizing large language models (LLMs) suggests a two-pronged approach to address the challenge of outlier activations. These outliers, which hinder efficient low-bit representation, are tackled by first employing a rotation transformation to redistribute outlier values across adjacent channels. This is done in a block-wise manner for computational efficiency, focusing on specific outlier dimensions identified beforehand. Then, a permutation transformation, specifically a zigzag pattern, is used to balance outlier distribution across these blocks, further smoothing the activation landscape and reducing block-wise variance. This dual approach, combining rotation and permutation, is superior to methods solely focused on smoothing because it directly addresses the spatial distribution of outliers rather than solely their magnitudes, leading to improved quantization results and ultimately enhancing the efficiency and capacity of quantized LLMs.
Quantization Methods#
The effectiveness of various quantization methods for compressing large language models (LLMs) is a central theme in current research. Post-training quantization (PTQ) methods are particularly attractive due to their efficiency, avoiding the computational cost of retraining. However, the presence of outlier activations, both normal (large values across many tokens) and massive (extremely large values in few tokens), pose significant challenges. Traditional methods often struggle to effectively handle massive outliers, leading to accuracy degradation in low-bit quantization. Advanced techniques like those employing rotation and permutation transformations show promise in redistributing outlier values, thus making quantization easier and more robust. Careful selection and application of these transformations, along with other techniques like smoothing, are crucial to managing both normal and massive outliers effectively and achieving high accuracy even with 4-bit quantization, which is desirable for resource-constrained environments. The choice between different PTQ approaches involves a trade-off between quantization efficiency, memory usage, and accuracy, and the optimal strategy may vary depending on the specific LLM and task.
LLM Quantization#
LLM quantization, the process of reducing the precision of large language model (LLM) parameters, presents a significant challenge. Outliers, both normal (relatively high magnitudes across all tokens) and massive (extremely high magnitudes in a few tokens), pose substantial difficulties. Traditional methods struggle to handle massive outliers, leading to performance degradation in low-bit quantization. Innovative approaches are needed to effectively mitigate both outlier types to achieve efficient low-bit representations. Strategies such as rotation and permutation transformations show promise by redistributing outlier values, facilitating smoother quantization and improved performance. Further research should focus on developing more sophisticated methods for handling outliers, potentially exploring adaptive techniques tailored to different LLM architectures and task characteristics. The development of quantization-friendly LLM architectures could further enhance efficiency.
Future Work#
Future research directions stemming from this work could explore several promising avenues. Extending DuQuant’s applicability to diverse LLM architectures beyond those tested (LLaMA, LLaMA2, Vicuna) is crucial to establish its generalizability and robustness. Investigating alternative outlier detection and mitigation strategies that complement or improve upon the rotation and permutation transformations would enhance DuQuant’s effectiveness. This might include exploring advanced matrix factorization techniques or employing novel smoothing methods tailored to massive outliers. A comprehensive theoretical analysis to formally explain DuQuant’s success and quantify its gains under different outlier distributions is needed. Furthermore, exploring different quantization techniques beyond uniform quantization is valuable, as well as examining the impact of various quantization schemes on downstream tasks. Finally, investigating optimal block sizes and permutation patterns for rotation matrices through more sophisticated optimization algorithms than greedy search could potentially yield further performance gains and computational efficiency. Incorporating dynamic block adaptation based on outlier distribution could further optimize performance.
More visual insights#
More on figures
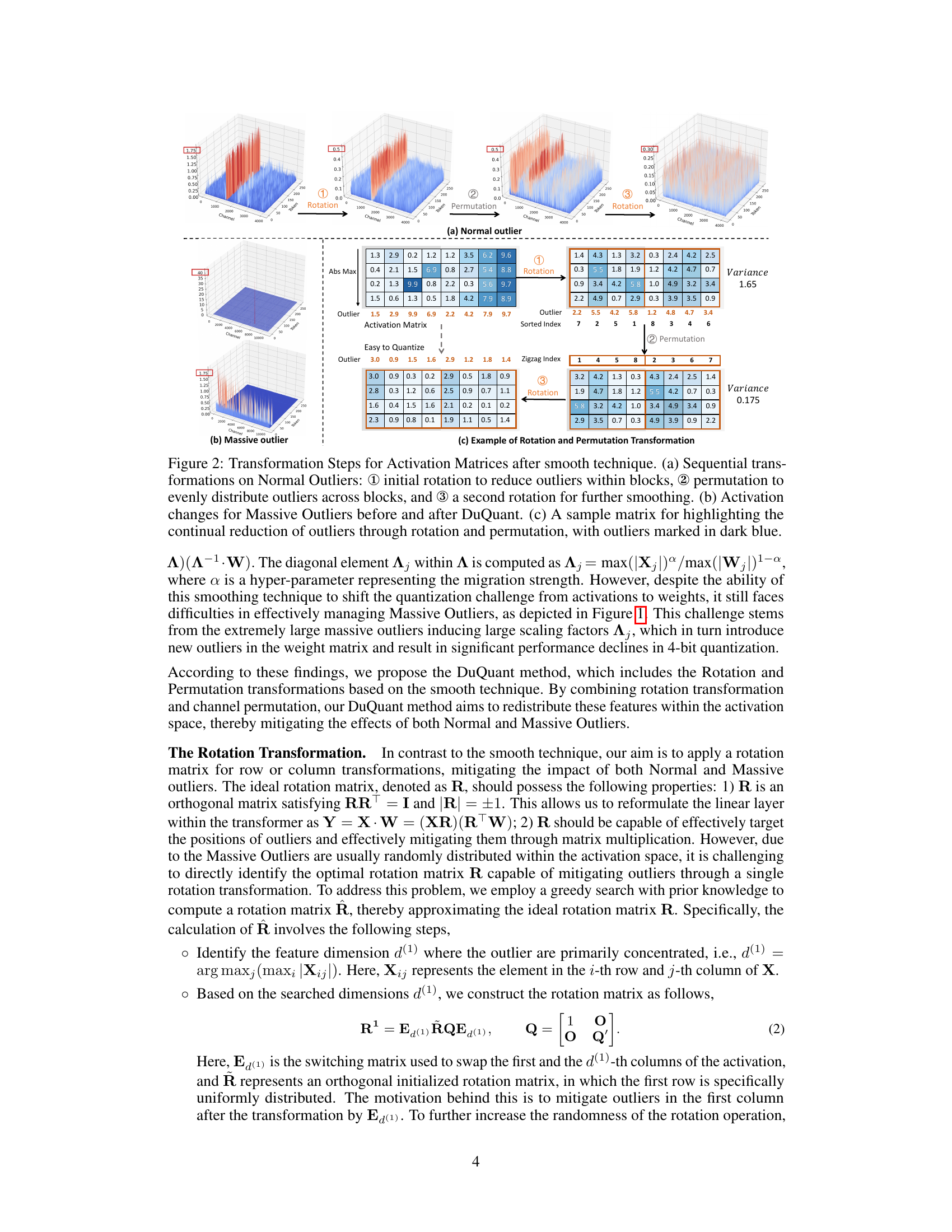
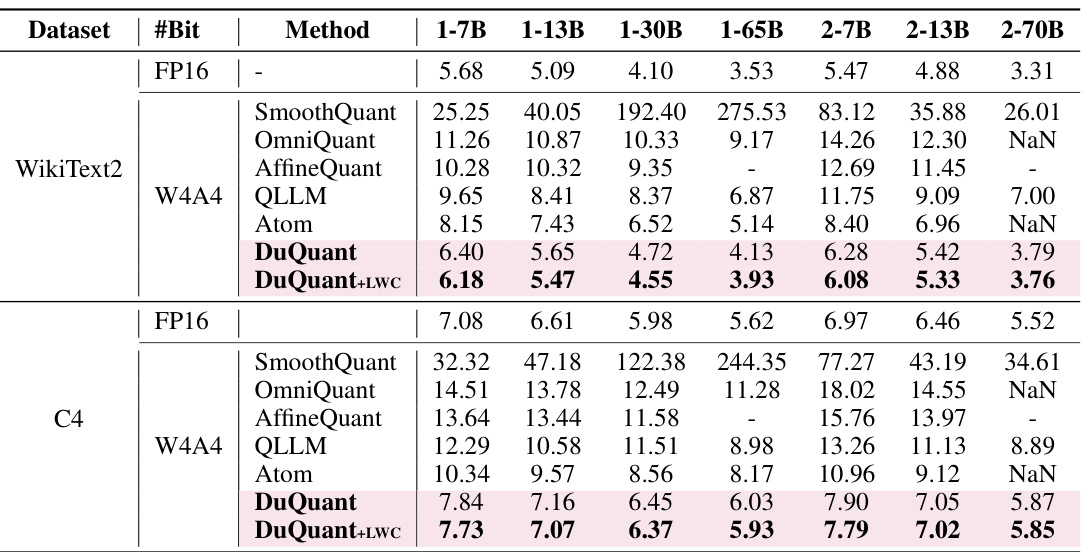
This figure illustrates the step-by-step process of DuQuant in handling both normal and massive outliers in activation matrices. Panel (a) shows the three-step process for normal outliers: an initial rotation to group outliers within blocks, a permutation to redistribute them evenly, and a final rotation for smoothing. Panel (b) compares the massive outlier distribution before and after DuQuant application, highlighting the effectiveness of the method. Panel (c) provides a concrete example of how the rotation and permutation transformations reduce outliers in a sample matrix.

This figure visualizes the different types of outliers found in the LLaMA2-7B model. Panel (a) shows Normal Outliers, which have relatively high magnitudes across many tokens. Panel (b) shows Massive Outliers, which have extremely high magnitudes but are present in only a few tokens. Panels (c) and (d) demonstrate that the SmoothQuant method struggles to effectively mitigate Massive Outliers, even leading to the creation of new outliers.
This figure illustrates the steps involved in the DuQuant method for handling activation outliers in LLMs. It shows how the method uses a combination of rotation and permutation transformations to reduce outliers. Panel (a) demonstrates the process for Normal Outliers, showing how initial rotation reduces outliers within blocks, then permutation distributes them evenly across blocks, and finally a second rotation further smooths the activations. Panel (b) displays the difference in Massive Outliers before and after applying DuQuant, highlighting its effectiveness. Panel (c) uses a sample matrix to visually depict the reduction of outliers through each step of the process.
This figure shows how the DuQuant method reduces outliers in activation matrices. It illustrates the three-step process: a rotation to reduce outliers within blocks, a permutation to evenly distribute outliers across blocks, and a final rotation for smoothing. The figure uses visualizations to demonstrate the effectiveness of the approach on both normal and massive outliers. A sample matrix is given to show the reduction of outliers after each transformation step.

This figure visualizes the different types of outliers found in the LLaMA2-7B model. Panel (a) shows Normal Outliers which have relatively high magnitudes across all tokens. Panel (b) displays Massive Outliers, characterized by extremely high values (around 1400) concentrated in a small number of tokens. Panels (c) and (d) demonstrate that the SmoothQuant method fails to effectively address these Massive Outliers; showing the persistence of large activations in the activation matrix (c) and the generation of new outliers in the weight matrix (d).
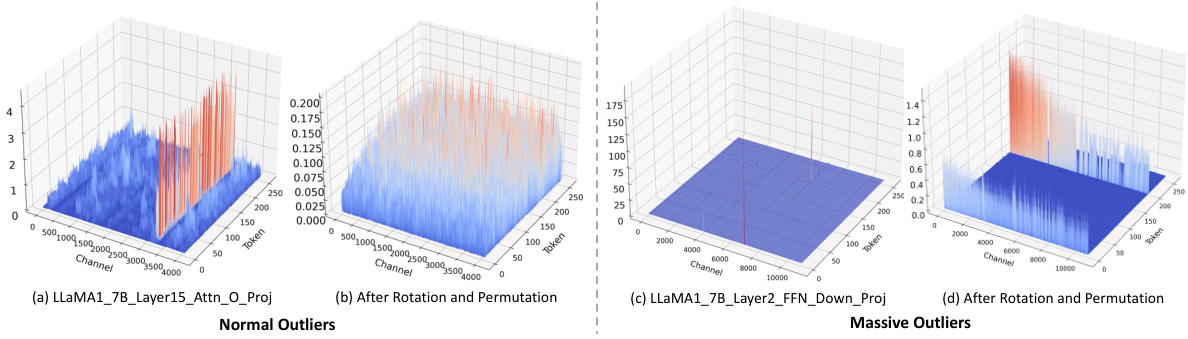
This figure visualizes the different types of outliers found in the LLaMA2-7B model. Panel (a) shows Normal Outliers, which are activations with relatively high magnitudes across all token sequences in the attention key projection. Panel (b) shows Massive Outliers, which are activations with extremely high magnitudes (around 1400) but only at very few tokens in the feed-forward network (FFN) down projection. Panels (c) and (d) demonstrate that the SmoothQuant method struggles to effectively mitigate Massive Outliers, showing its failure to eliminate these outliers and even resulting in the emergence of new outliers in both the activation and weight matrices.
This figure visualizes the different types of outliers (Normal and Massive) found in the LLaMA2-7B model. Panel (a) shows Normal Outliers as relatively high activation magnitudes across all tokens. Panel (b) shows Massive Outliers as extremely high magnitudes in a small subset of tokens. Panels (c) and (d) demonstrate that the SmoothQuant method struggles to effectively handle Massive Outliers, even leading to the creation of new outliers in the weight matrix.

This figure visualizes the different types of outliers found in the LLaMA2-7B model. Panel (a) shows Normal Outliers, which have relatively high magnitudes across all tokens. Panel (b) shows Massive Outliers, which have extremely high magnitudes at very few tokens. Panel (c) demonstrates the failure of SmoothQuant to effectively mitigate Massive Outliers in the activation matrix, and Panel (d) shows that SmoothQuant even introduces new outliers in the weight matrix.
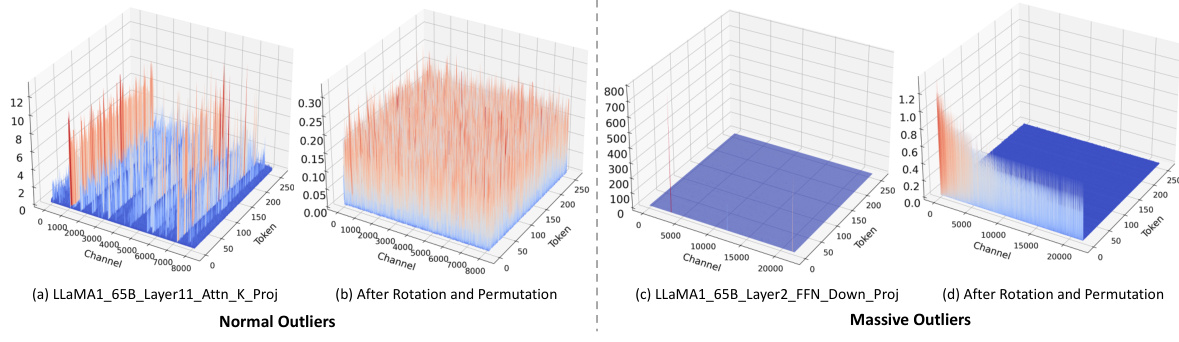
This figure visualizes different types of outliers in the LLaMA2-7B model. Panel (a) shows Normal Outliers with relatively high magnitudes across all tokens. Panel (b) shows Massive Outliers with extremely high magnitudes (around 1400) in very few tokens. Panels (c) and (d) illustrate the failure of SmoothQuant to effectively handle Massive Outliers, highlighting its struggle and the emergence of new outliers after applying the method.
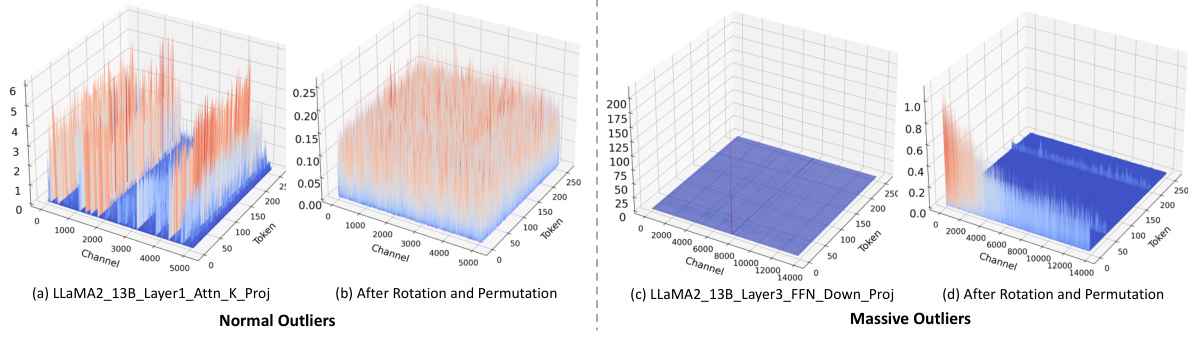
This figure visualizes the different types of outliers present in the LLaMA2-7B model. Panel (a) shows normal outliers with relatively high magnitudes across all tokens. Panel (b) shows massive outliers with extremely large values (around 1400) concentrated on very few tokens. Panels (c) and (d) demonstrate the ineffectiveness of SmoothQuant in handling massive outliers, showing that it fails to eliminate them and even introduces new outliers in both the activation and weight matrices.
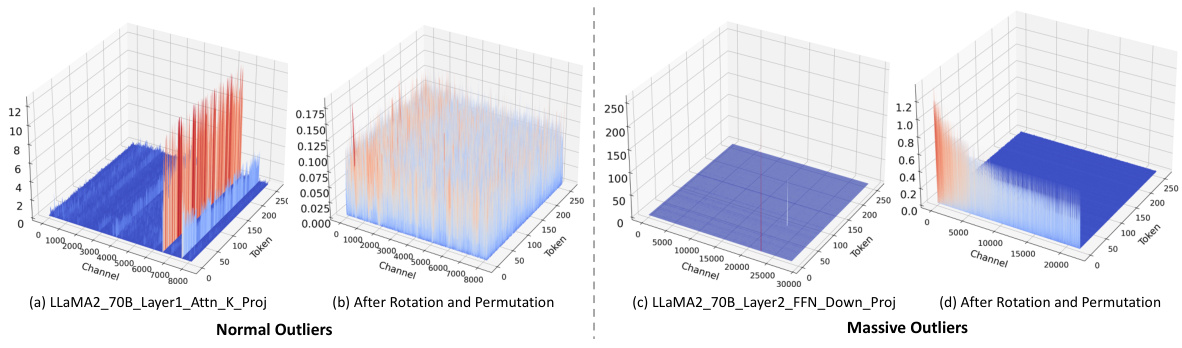
This figure visualizes the different types of outliers present in the LLaMA2-7B model. Panel (a) shows Normal Outliers, which have relatively high magnitudes across all tokens. Panel (b) shows Massive Outliers, characterized by extremely high values present in only a few tokens. Panels (c) and (d) demonstrate that the SmoothQuant method struggles to effectively address Massive Outliers, highlighting its limitations in handling these types of outliers during quantization.
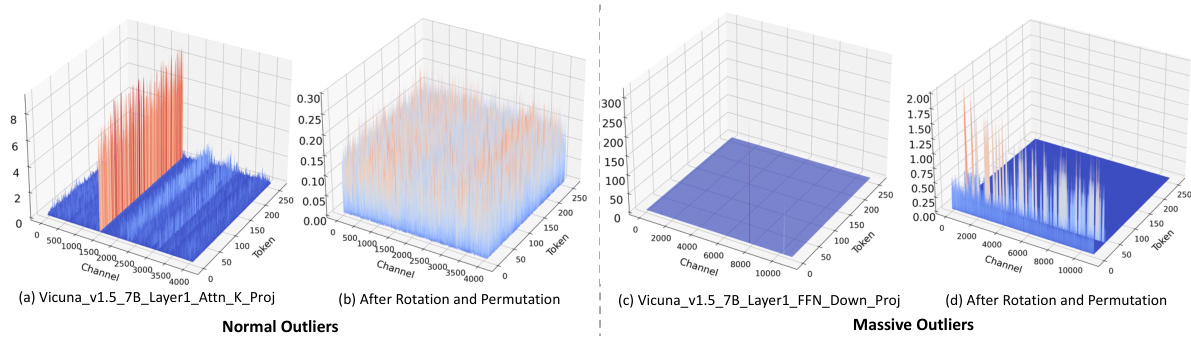
This figure visualizes different types of outliers in the LLaMA2-7B model. (a) shows Normal Outliers with relatively high magnitudes across all tokens. (b) shows Massive Outliers with extremely high magnitudes at a few tokens. (c) and (d) illustrate the limitations of SmoothQuant in handling Massive Outliers, showing that it fails to eliminate them and even creates new outliers in the weight matrix.
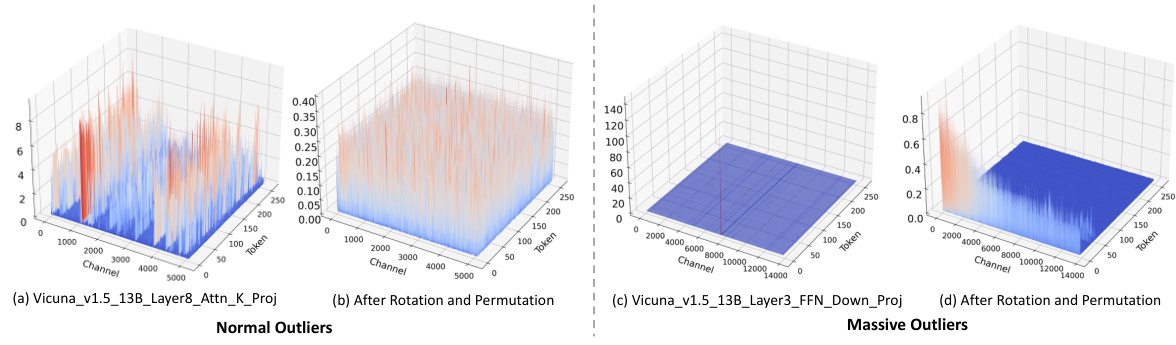
This figure visualizes the different types of outliers present in the LLaMA2-7B model. (a) and (b) show the distribution of normal and massive outliers in the activation matrices of the attention key projection and FFN down projection layers, respectively. (c) and (d) demonstrate the ineffectiveness of SmoothQuant in handling massive outliers, showing that it fails to eliminate them and even introduces new outliers in the weight matrix.
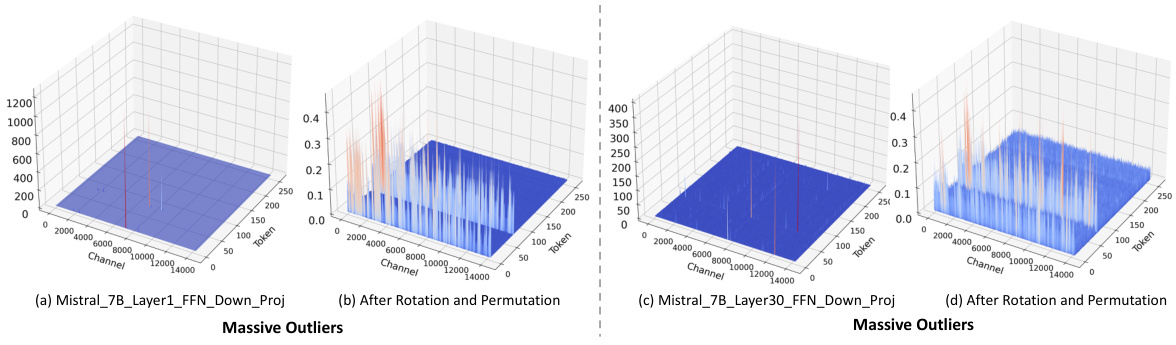
This figure visualizes the different types of outliers found in the LLaMA2-7B model. Panel (a) shows Normal Outliers, which have relatively high magnitudes across all tokens. Panel (b) shows Massive Outliers, which are extremely large values found in a small number of tokens. Panels (c) and (d) demonstrate the limitations of the SmoothQuant method in handling these Massive Outliers, showing that it fails to completely eliminate them and even introduces new outliers in the weights.
More on tables
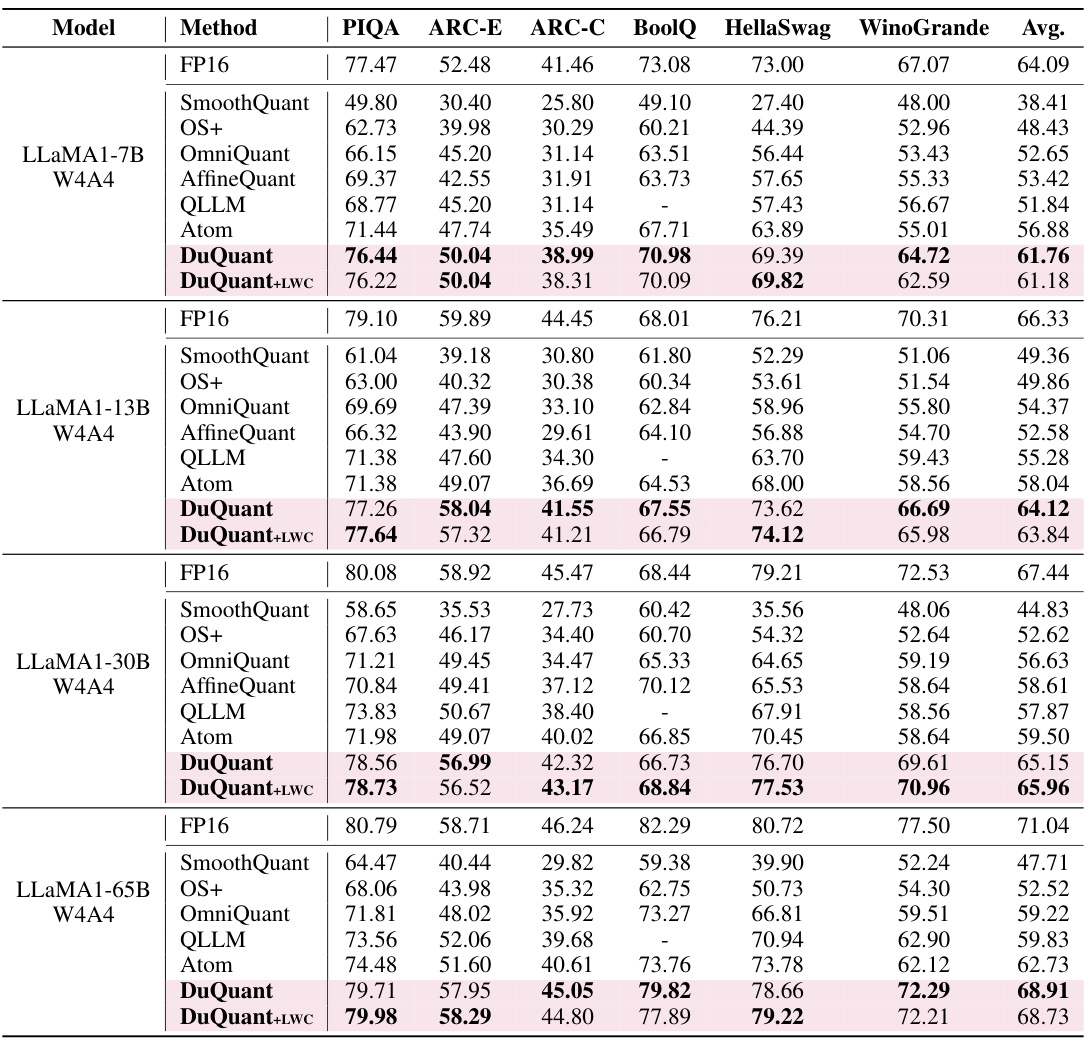
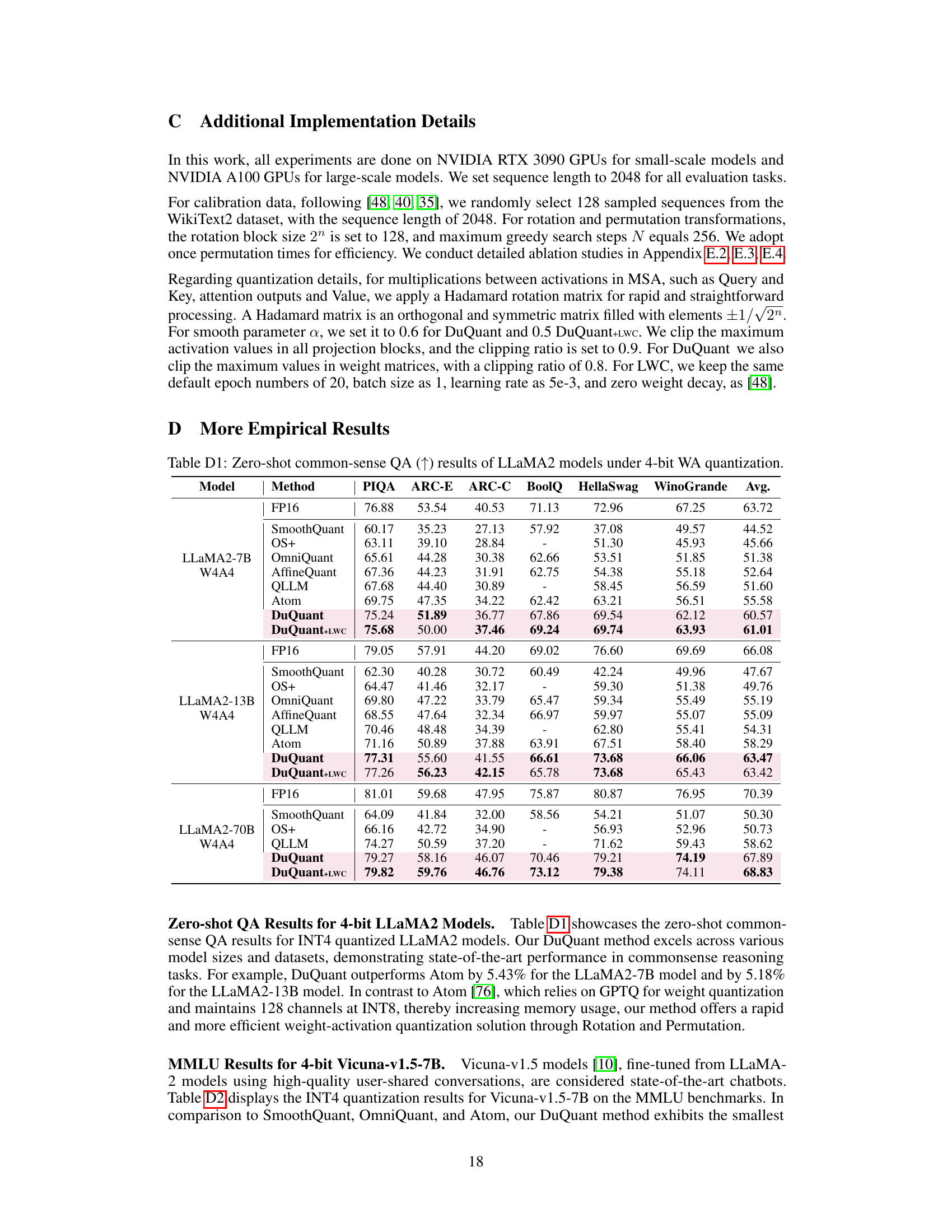
This table presents the zero-shot results for several question answering tasks using the LLaMA1 model with 4-bit weight-activation quantization. It shows the performance of different quantization methods (FP16, SmoothQuant, OS+, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) across various datasets (PIQA, ARC-E, ARC-C, BoolQ, HellaSwag, and WinoGrande). The table highlights the performance improvements achieved by DuQuant compared to the baselines.

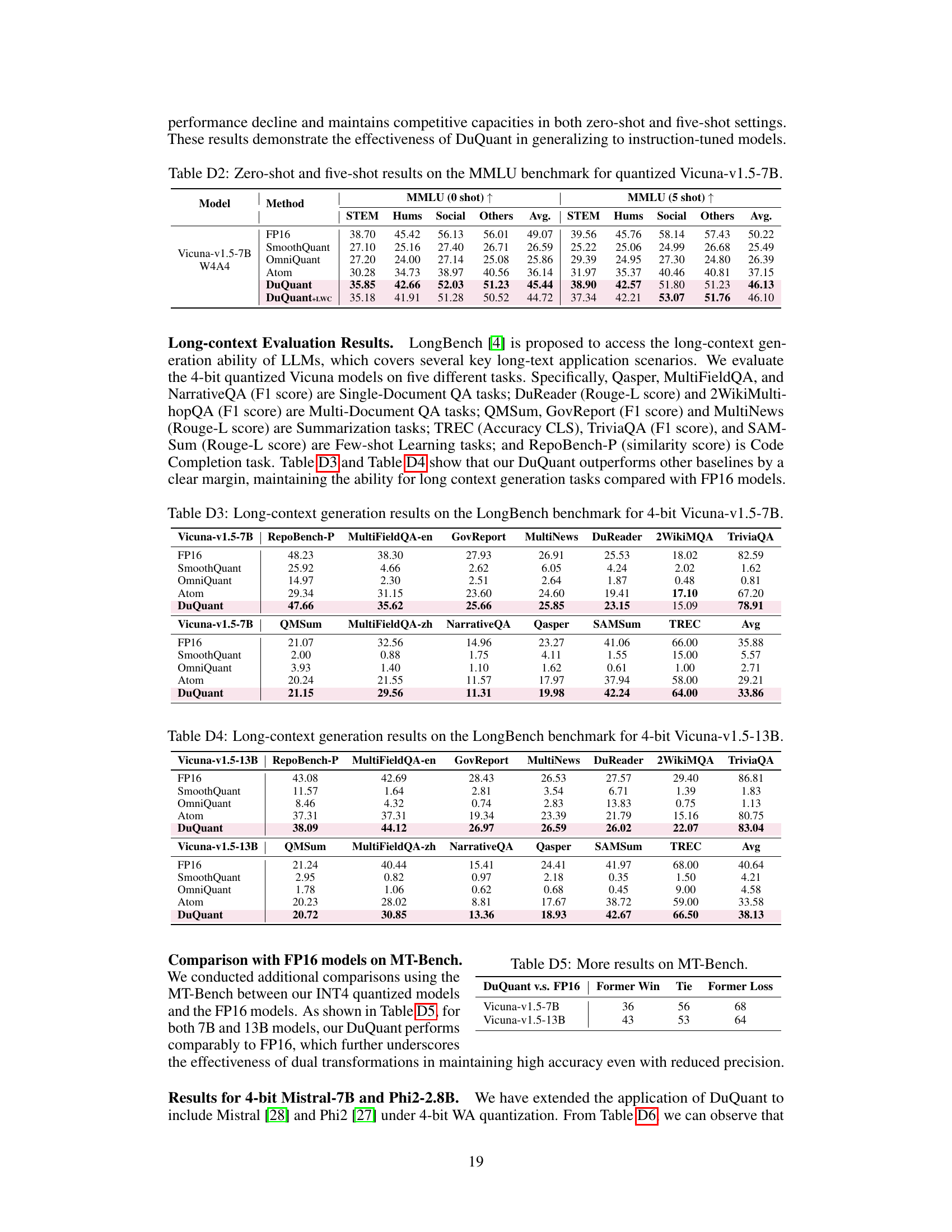
This table shows the zero-shot and five-shot performance of the Vicuna-v1.5-13B language model on the MMLU benchmark after applying 4-bit weight-activation quantization using the DuQuant method. It compares the results to several baselines (SmoothQuant, OmniQuant, Atom), showing the effectiveness of DuQuant on this instruction-tuned model. The results are broken down by category (STEM, Hums, Social, Others) for both zero-shot and five-shot settings.
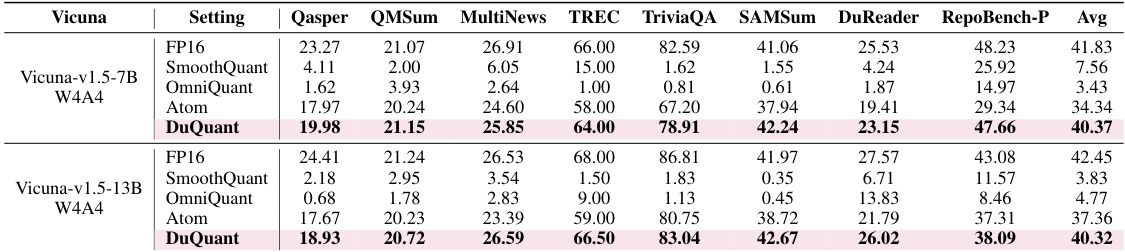
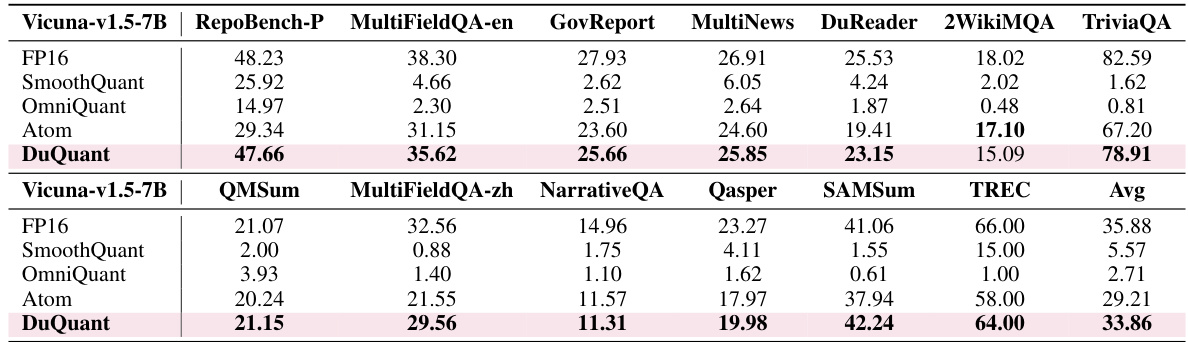
This table presents the results of long-context generation experiments using 4-bit quantized Vicuna models. It shows the performance of different quantization methods (SmoothQuant, OmniQuant, Atom, and DuQuant) compared to the full-precision (FP16) model on various long-context generation tasks from the LongBench benchmark. The tasks cover different aspects of long-form text generation, including question answering, summarization, and code generation. The scores for each task provide a comprehensive evaluation of the models’ abilities to generate high-quality text in long-context scenarios.
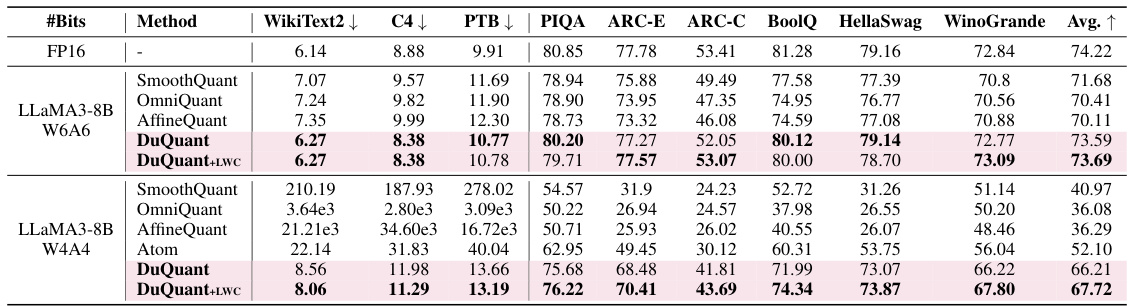
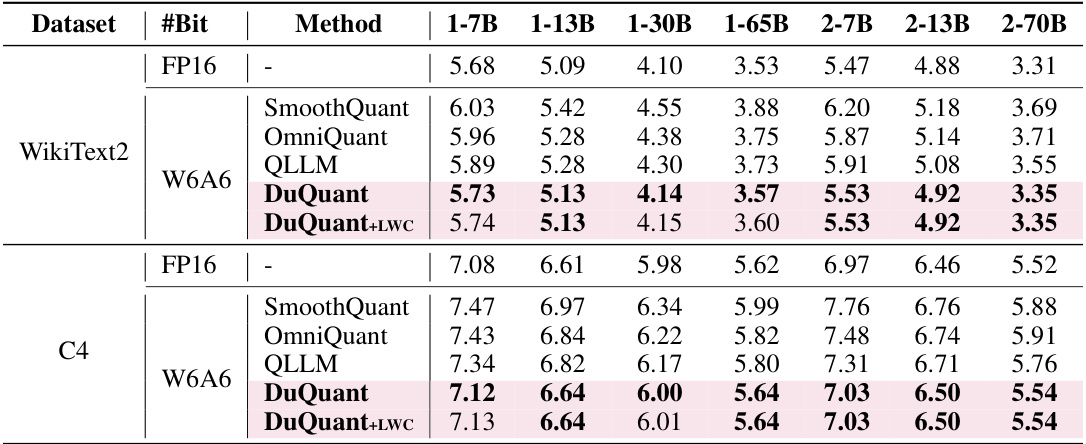
This table presents the perplexity scores achieved by different quantization methods on the WikiText2 and C4 datasets using 4-bit weight and activation quantization. Lower perplexity values indicate better performance. The table compares DuQuant and DuQuant+LWC against several baselines (SmoothQuant, OmniQuant, AffineQuant, QLLM, Atom) across various LLM sizes (1-7B, 1-13B, 1-30B, 1-65B, 2-7B, 2-13B, 2-70B). Note that Atom and OmniQuant results are incomplete for the LLaMA2-70B model.
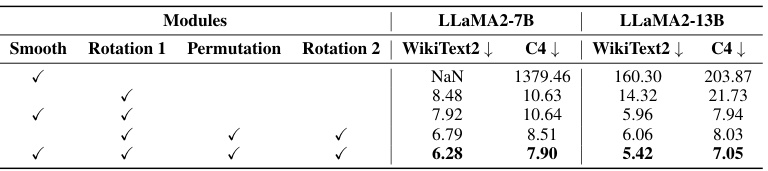
This table presents the ablation study of different components in the DuQuant model. By removing or adding different components (smooth, rotation 1, permutation, rotation 2), the table shows the effect of each component on the final performance (WikiText2 and C4 perplexity) of the model using 4-bit weight-activation quantization. It demonstrates the incremental improvement of the model’s performance by adding these components.

This table presents the results of an ablation study evaluating the impact of different outlier types (Normal and Massive) on quantization performance when only using the smoothing technique. It shows the perplexity scores (lower is better) on the WikiText2 and C4 datasets for LLaMA2-7B and LLaMA2-13B models under different outlier handling scenarios. The results highlight that Massive outliers have a significantly more negative impact on quantization accuracy than Normal outliers.
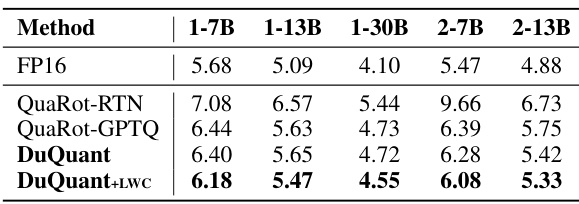
This table presents the perplexity scores achieved by different quantization methods (SmoothQuant, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) on the WikiText2 and C4 datasets using 4-bit weight-activation quantization. Lower perplexity scores indicate better performance. The table compares results across various LLM sizes (1-7B, 1-13B, 1-30B, 1-65B, 2-7B, 2-13B, 2-70B), providing a comprehensive evaluation of each method’s effectiveness in handling low-bit quantization.
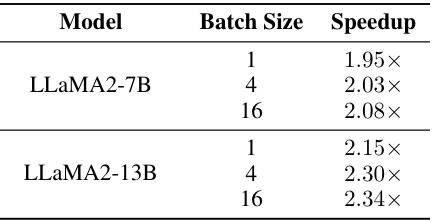
This table presents the layer-wise speedup achieved by DuQuant during the pre-filling stage for 4-bit weight-activation quantization. It shows the speedup factor obtained for different batch sizes (1, 4, and 16) on two different models, LLaMA2-7B and LLaMA2-13B. The results highlight the significant performance improvement gained by using DuQuant during the pre-filling phase of LLM inference.

This table presents the perplexity scores achieved by different methods for quantizing LLMs using 4-bit weight-activation quantization. Lower perplexity indicates better performance. The table compares DuQuant and DuQuant+LWC against several state-of-the-art baseline methods across various LLM sizes (7B, 13B, 30B, 65B) from LLaMA and LLaMA2. Results are shown for WikiText2 and C4 datasets. Note that Atom and OmniQuant did not process group-query attention for LLaMA2-70B.
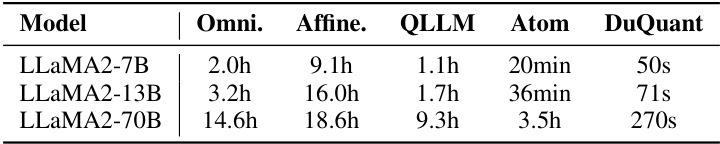
This table presents the runtime comparison of different quantization methods (OmniQuant, AffineQuant, QLLM, Atom, and DuQuant) for three different LLaMA2 models (7B, 13B, and 70B) on a single NVIDIA A100 GPU. The results highlight DuQuant’s significant speed advantage over other methods, showing its efficiency in the quantization process.
This table presents the perplexity scores achieved by different quantization methods (SmoothQuant, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) on the WikiText2 and C4 datasets, using 4-bit weight-activation quantization. Lower perplexity indicates better performance. The table compares results across different sizes of LLaMA and LLaMA2 language models. DuQuant+LWC represents DuQuant with learnable weight clipping.
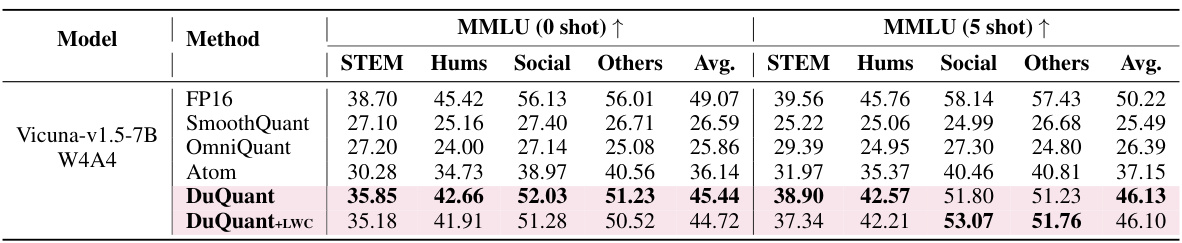
This table presents the zero-shot and five-shot results of the Vicuna-v1.5-13B model on the MMLU benchmark using 4-bit weight-activation quantization. It compares the performance of different quantization methods (FP16, SmoothQuant, OmniQuant, Atom, DuQuant, and DuQuant+LWC) across different subcategories of the MMLU benchmark (STEM, Hums, Social, Others) and provides the average performance across all subcategories. The table shows that DuQuant achieves competitive results compared to the full precision (FP16) model, particularly in the five-shot setting.
This table presents the zero-shot results on several question answering datasets for different sizes of LLaMA1 models using 4-bit weight and activation quantization. It compares the performance of DuQuant against other state-of-the-art quantization methods (SmoothQuant, OS+, OmniQuant, AffineQuant, QLLM, Atom). The table shows the accuracy scores for each model on different datasets (PIQA, ARC-E, ARC-C, BoolQ, HellaSwag, WinoGrande) and the average accuracy across all datasets.

This table presents the zero-shot results for several common sense question answering tasks on the LLaMA1 model with 4-bit weight-activation quantization. It shows the performance of different quantization methods (SmoothQuant, OS+, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) compared to the full precision (FP16) baseline. The results are given for different model sizes (7B, 13B, 30B, and 65B parameters). Additional results for LLaMA2 models and 6-bit quantization are available in the supplementary materials.

This table shows the zero-shot and five-shot results of the Vicuna-v1.5-13B model on the MMLU benchmark under 4-bit weight-activation quantization. It compares the performance of different quantization methods (FP16, SmoothQuant, OmniQuant, Atom, DuQuant, DuQuant+LWC) across various sub-categories of the MMLU benchmark (STEM, Hums, Social, Others). The results highlight the relative performance gains of DuQuant compared to other state-of-the-art quantization techniques.
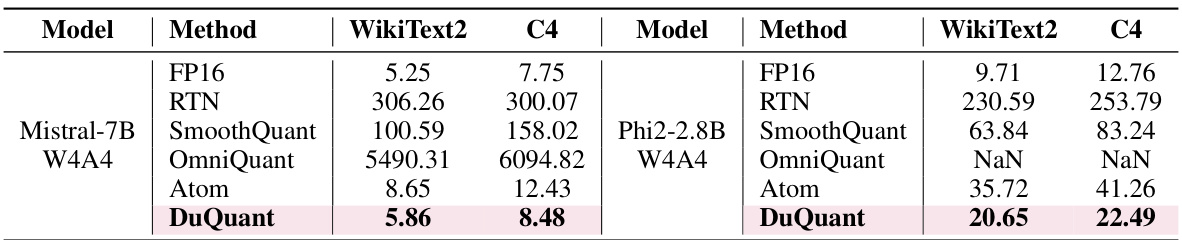
This table shows the perplexity results on WikiText2 and C4 datasets for Mistral-7B and Phi2-2.8B models under 4-bit weight-activation quantization. It compares the performance of several different quantization methods (FP16, RTN, SmoothQuant, OmniQuant, Atom, and DuQuant) to highlight the effectiveness of the DuQuant method, particularly in handling the challenges posed by massive outliers present in these models.

This table presents the perplexity scores achieved by various LLMs using different quantization methods. Lower perplexity values indicate better performance. The table compares the performance of DuQuant against several state-of-the-art baseline methods for 4-bit weight-activation quantization across different sizes of LLMs. Results are shown for WikiText2 and C4 datasets. Note that Atom and OmniQuant did not process the group-query attention for LLaMA2-70B.
This table presents the perplexity scores achieved by different quantization methods (SmoothQuant, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) on the WikiText2 and C4 datasets using 4-bit weight-activation quantization. Lower perplexity scores indicate better performance. The table compares these methods against a floating-point (FP16) baseline across various sizes of LLaMA and LLaMA2 models. Note that Atom and OmniQuant did not process group-query attention for LLaMA2-70B, and the W6A6 results are in Table D8.

This table shows the zero-shot results of the LLaMA1 model using 4-bit weight-activation quantization on several question answering tasks. It compares the performance of different quantization methods (SmoothQuant, OS+, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) against the full precision floating point model (FP16). The results are presented as the accuracy achieved on each task (PIQA, ARC-E, ARC-C, BoolQ, HellaSwag, WinoGrande), and an average accuracy across all tasks. The table also indicates that similar results for LLaMA2 models and using 6-bit quantization can be found in other tables within the appendix.
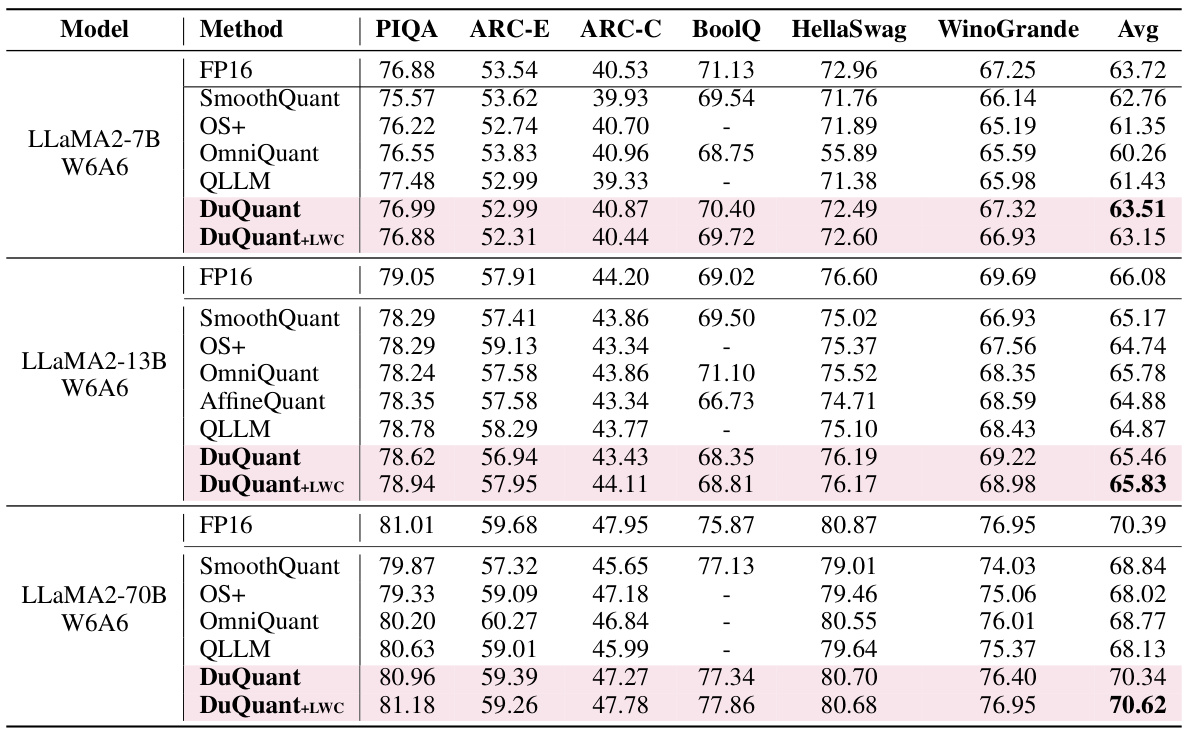
This table presents the results of zero-shot question answering (QA) experiments conducted on several LLaMA1 models using 4-bit weight-activation quantization. It compares the performance of different quantization methods (FP16, SmoothQuant, OS+, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) across six different QA datasets (PIQA, ARC-E, ARC-C, BoolQ, HellaSwag, and WinoGrande). The table shows the average accuracy across all datasets for each method and model. Additional results for LLaMA2 models and using 6-bit quantization are available in supplementary tables.
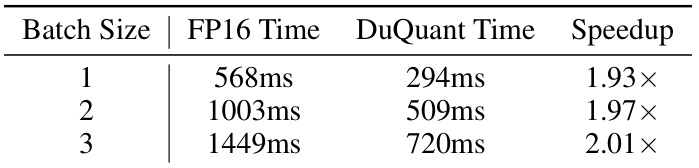
This table presents the end-to-end pre-filling speedup results on the LLaMA2-7B model. It shows the time taken for pre-filling using FP16 and DuQuant at different batch sizes (1, 2, and 3). The speedup is calculated as the ratio of FP16 time to DuQuant time for each batch size. The results demonstrate the efficiency gains achieved by DuQuant in the pre-filling phase of LLM inference.
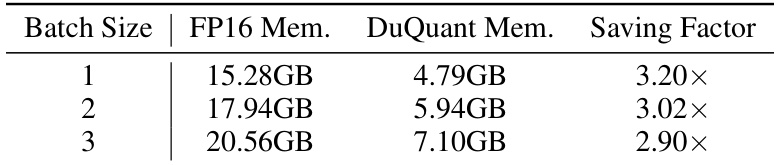
This table shows the peak memory usage (in GB) for the LLaMA2-7B model during the pre-filling phase under different batch sizes (1, 2, and 3). It compares the memory usage of the FP16 model with the DuQuant quantized model. The ‘Saving Factor’ column indicates the reduction in memory usage achieved by DuQuant compared to FP16 for each batch size. The results highlight the significant memory savings offered by DuQuant, particularly at smaller batch sizes.

This table presents the results of a decoding phase experiment on a single LLaMA2-7B layer using a batch size of 64. It compares the time taken and memory usage of different quantization methods: FP16 (full precision), SmoothQuant, QLLM, QuaRot, and DuQuant. The time is measured in milliseconds (ms), and the memory is in gigabytes (GB). The table also shows the saving factor for time and memory usage compared to the FP16 baseline. The OOM (Out Of Memory) entry for QLLM indicates that this method exceeded the available memory. The results illustrate the relative efficiency of different quantization approaches during the decoding phase of LLM inference.
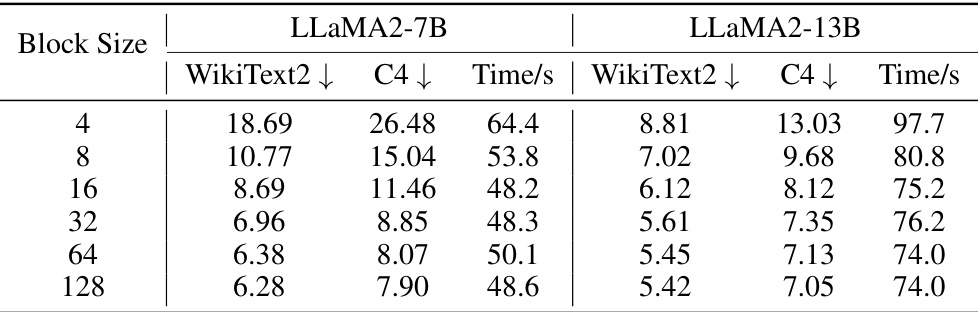
This table presents the results of an ablation study on the impact of rotation block size on the performance of the quantized models. The experiment was conducted on LLaMA2-7B and LLaMA2-13B models. The table shows that increasing block size generally improves model performance, likely due to more efficient transformations during the reshaping of original activation/weight matrices. The perplexity on WikiText2 and C4 datasets, and the runtime are shown for different block sizes (4, 8, 16, 32, 64, 128).
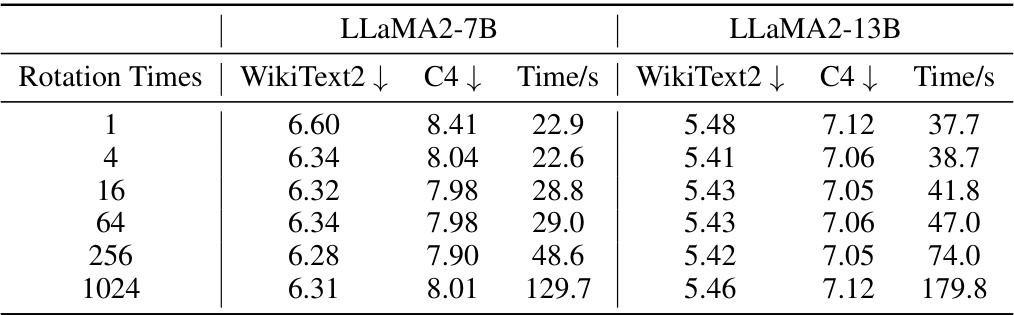
This table presents the results of an ablation study on the number of rotation times used in the DuQuant method. The study was conducted on LLaMA2-7B and LLaMA2-13B models using different rotation times (1, 4, 16, 64, 256, 1024). The table shows the perplexity on WikiText2 and C4 datasets, as well as the time taken for each setting. The results indicate that increasing the number of rotations initially improves performance, but excessive rotations can lead to overfitting.

This table presents a comparison of different permutation algorithms used in the DuQuant method. It shows the WikiText2 and C4 perplexity scores, the variance of activation magnitudes across blocks, and the computation time for each algorithm (w.o. Permutation, Random, Simulated Annealing, Zigzag). The results demonstrate the effectiveness of the Zigzag permutation in reducing variance while maintaining computational efficiency.

This table presents the results of applying the DuQuant method with randomly generated calibration data instead of using actual data from WikiText2 and C4 datasets. This tests the robustness of DuQuant against varying calibration settings, demonstrating the method’s adaptability and performance even without specific calibration data.
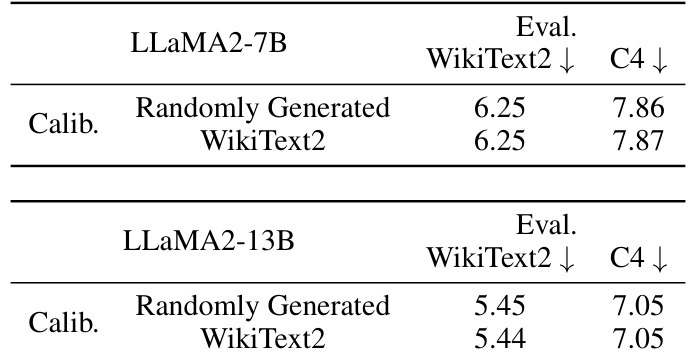
This table presents the results of applying the DuQuant method to the LLaMA2-7B and LLaMA2-13B models using randomly generated calibration data instead of data from WikiText2. It demonstrates the robustness of DuQuant, showing that it achieves comparable performance even without using specific calibration data.
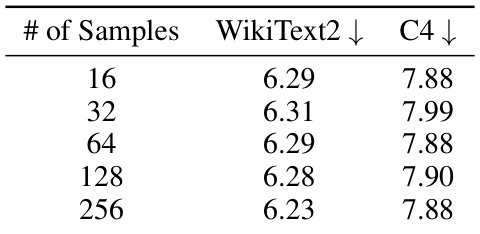
This table presents the results of an ablation study conducted to evaluate the impact of varying the number of calibration samples used in the DuQuant quantization method on the LLaMA2-7B model. The study explores how changing the number of samples (16, 32, 64, 128, and 256) affects the performance of the quantized model, measured in terms of perplexity on the WikiText2 and C4 datasets. The results show that the quantization performance is relatively insensitive to the number of calibration samples used, indicating that the averaging process inherent to DuQuant reduces the influence of individual samples on the final results. This robustness is a key advantage of the approach.

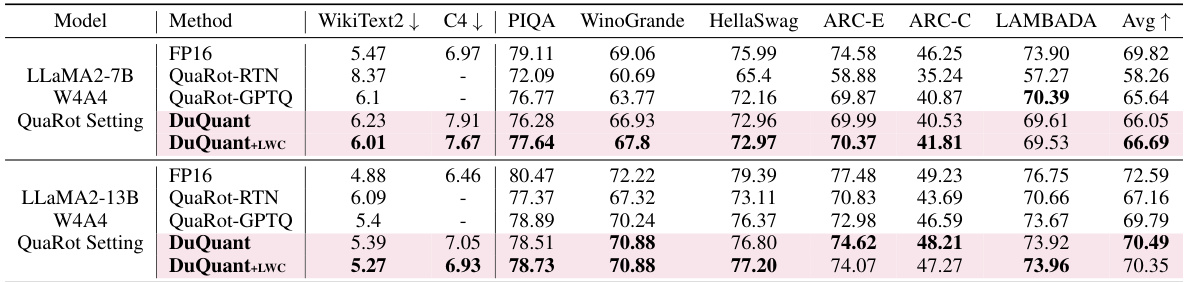
This table compares the quantization settings used in the QuaRot and DuQuant methods. It shows that QuaRot uses per-channel symmetric quantization for weights and per-token symmetric quantization for activations, while keeping query inputs in FP16 precision. In contrast, DuQuant employs per-channel asymmetric quantization for weights, per-token asymmetric quantization for activations, and per-token asymmetric quantization for query inputs. This highlights a key difference in the approaches taken by the two methods.
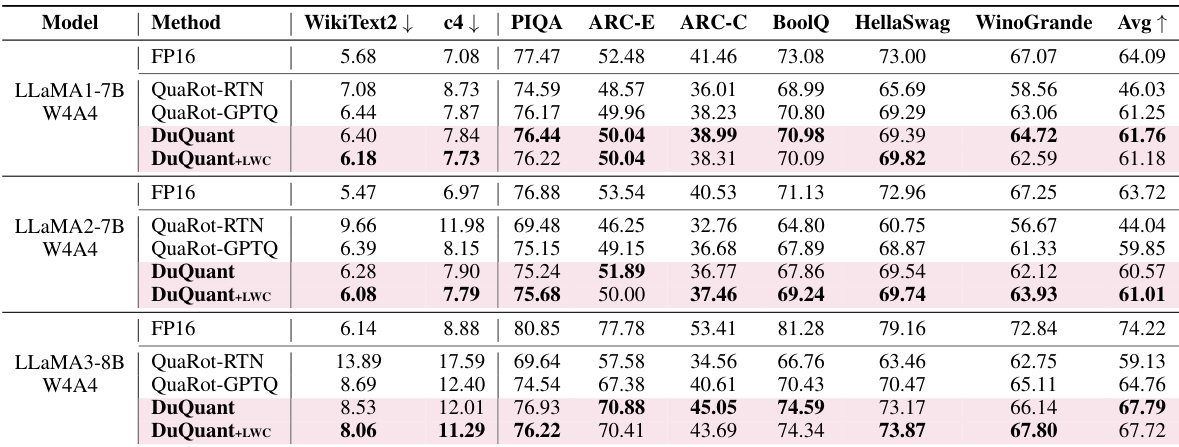
This table presents the perplexity scores achieved by different quantization methods (SmoothQuant, OmniQuant, AffineQuant, QLLM, Atom, DuQuant, and DuQuant+LWC) on the WikiText2 and C4 datasets using 4-bit weight-activation quantization. Lower perplexity scores indicate better performance. The table compares the performance across various sizes of LLaMA and LLaMA2 models. Note that Atom and OmniQuant’s results for the LLaMA2-70B model are incomplete due to unprocessed group-query attention.
This table presents the results of zero-shot question answering experiments conducted on four different sizes of the LLaMA1 large language model, each quantized using a 4-bit weight-activation method. The table shows the performance of the models on six different tasks (PIQA, ARC-E, ARC-C, BoolQ, HellaSwag, WinoGrande), along with an average score across all six tasks. The results are compared to a floating-point (FP16) baseline, highlighting the effectiveness of the quantization technique. The table also notes that results for LLaMA2 models and using a 6-bit weight-activation method are available in other tables within the paper’s supplementary material.

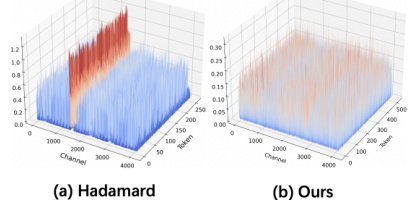
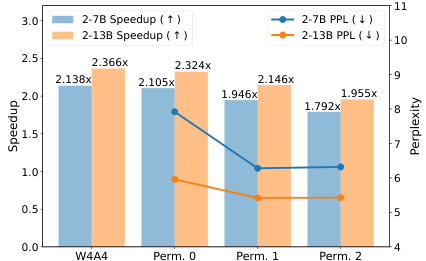
This table compares the performance of DuQuant and QuaRot on the WikiText2 and C4 datasets for the LLaMA2-7B and LLaMA2-13B models using W4A4 (4-bit weight and activation) quantization. It highlights the perplexity scores achieved by each method, offering a direct comparison of the two approaches on these benchmark datasets. The table demonstrates that DuQuant is superior to QuaRot in terms of achieving lower perplexity, suggesting a more effective quantization strategy.

This table presents a comparison of the quantization runtime for different models (LLaMA2-7B, LLaMA2-13B, and LLaMA2-70B) using various quantization methods (OmniQuant, AffineQuant, QLLM, Atom, and DuQuant) on a single NVIDIA A100 GPU. The results highlight the significant speedup achieved by DuQuant compared to other methods.
Full paper#