Scale Equivariant Graph Metanetworks

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel framework that significantly improves the performance of neural network processing by incorporating scaling symmetries, a previously under-explored area. It also opens new avenues for research into NN processing and expands the applicability of metanetworks to various domains, potentially revolutionizing problem-solving in numerous fields. This is particularly relevant to the growing field of Implicit Neural Representations (INRs).

Visual Insights

#

This figure shows the distribution of the norms of weights and biases for each layer of the CNNs in the CIFAR-10-GS dataset that use ReLU activation function. The distributions are shown separately for weights and biases in each of the four layers of the CNNs. The x-axis represents the norm values, and the y-axis represents the frequency of occurrence of those norm values. The distributions suggest that weights and biases are not uniformly distributed in norm, with some norm values being more frequent than others. This information is used in the paper to understand and analyze the scaling symmetries present in the datasets.

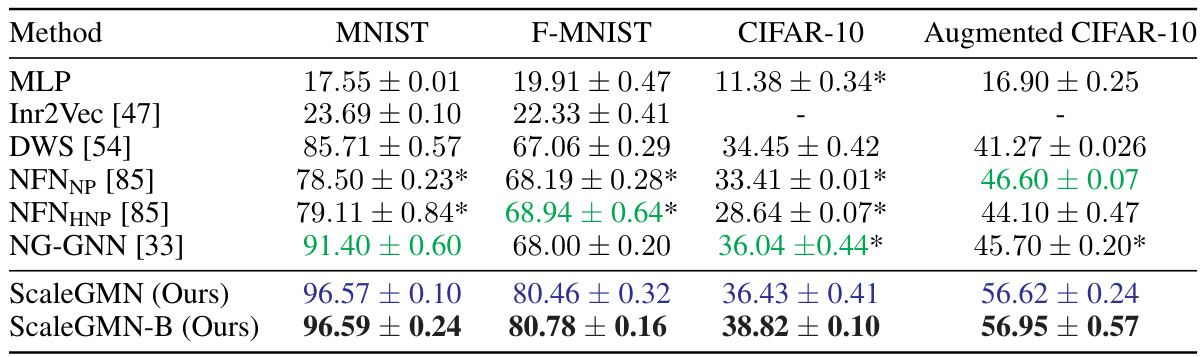
This table presents the results of INR classification experiments conducted on four datasets: MNIST, F-MNIST, CIFAR-10, and Augmented CIFAR-10. Multiple methods were used, including the authors’ ScaleGMN and a baseline MLP. The table shows the mean and standard deviation of the test accuracy across three different random seeds. Asterisks (*) indicate baselines whose results are reported as they appear in the original papers, whereas the others are newly trained by the authors of this paper for direct comparison. Colors highlight the top three performing methods for each dataset.

In-depth insights

#

Scale Equivariance

#

The concept of ‘Scale Equivariance’ introduces a crucial advancement in neural network processing by acknowledging that neural networks possess inherent symmetries beyond just permutation invariance. The paper explores the concept of scaling symmetries, where non-zero scalar multiplications and divisions of weights and biases leave the network function unchanged. This is particularly relevant for activation functions like sine, ReLU, and tanh, which exhibit such symmetries. Scale Equivariant Graph MetaNetworks (ScaleGMNs) are proposed as a framework that incorporates these symmetries, making neuron and edge representations equivariant to valid scalings. The core of this framework involves novel building blocks that ensure equivariance or invariance under scalar multiplication or products thereof, ultimately providing a more powerful inductive bias for NN processing. A key contribution is the demonstration that ScaleGMNs can simulate the forward and backward pass of any input feedforward neural network, which highlights the potential of this approach for processing and interpreting the information stored within neural network parameters.

GMN Framework

#

The Graph MetaNetwork (GMN) framework, as discussed in the research paper, presents a novel method for processing neural networks by leveraging their inherent symmetries. Unlike previous methods focusing solely on permutation symmetries, GMN integrates scaling symmetries, offering a more comprehensive and powerful approach. This involves creating a graph representation of the neural network, where nodes represent neurons and edges represent weights. The framework then employs message-passing algorithms to process this graph, ensuring equivariance (or invariance) to both permutation and scaling transformations. This is a crucial advancement, as it incorporates additional symmetries often neglected in prior work, thereby enhancing the expressive power of the model. The introduction of scaling equivariance is particularly significant because it directly addresses the symmetries present in many common activation functions (ReLU, tanh, sine), allowing the framework to better model the underlying functions. Furthermore, this approach demonstrates enhanced performance across various datasets and tasks, underlining the utility of considering scaling symmetries in neural network processing. ScaleGMN’s capability to simulate the forward and backward pass of any input feedforward neural network adds a distinct advantage. It allows for reconstruction of NN functions and gradients which could unlock various downstream applications.

Symmetries in NN

#

Neural network (NN) symmetries represent transformations of NN parameters that leave the network’s function unchanged. Understanding these symmetries is crucial for improving NN design, training, and interpretation. Permutation symmetries, where interchanging hidden neurons doesn’t alter the output, have been extensively studied and utilized in architectures like graph metanetworks. However, scaling symmetries, involving non-zero scalar multiplications of weights and biases, offer a less explored area with significant potential. These symmetries, arising from the activation functions themselves, can lead to more efficient and expressive network designs. The paper highlights the significance of scaling symmetries by proposing a novel framework called ScaleGMN, demonstrating superior performance compared to traditional methods, indicating that incorporation of scaling symmetries improves inductive bias, leading to more accurate and generalizable results. Future research should further explore the implications and applications of scaling symmetries in various NN processing domains.

ScaleGMN Results

#

The ScaleGMN results section would ideally present a comprehensive evaluation of the proposed model’s performance across various tasks and datasets. Key aspects to include would be quantitative metrics demonstrating improved accuracy compared to state-of-the-art baselines on tasks like INR classification, INR editing, and generalization prediction. The results should showcase ScaleGMN’s effectiveness across different activation functions (ReLU, tanh, sine), highlighting the model’s adaptability and the benefits of incorporating scaling symmetries. Crucially, the results should be statistically significant, ideally using multiple trials with error bars to demonstrate reliable performance gains. Detailed ablation studies investigating the impact of individual components of ScaleGMN, such as scale-equivariant message passing and different canonicalization techniques, are essential. Finally, qualitative analysis, perhaps including visualizations of INR edits, could provide further insights into the model’s behavior and capabilities. A thorough analysis would solidify the paper’s claims about ScaleGMN’s improved performance and highlight the benefits of scale equivariance for neural network processing.

Future Directions

#

Future research could explore extending ScaleGMNs to diverse neural network architectures beyond FFNNs and CNNs, handling complexities like skip connections and normalization layers. Investigating the theoretical expressive power of ScaleGMNs, particularly regarding their ability to approximate arbitrary functionals and operators, is crucial. A comprehensive analysis of the impact of different activation functions and scaling groups on performance is needed. Furthermore, developing efficient training strategies and addressing potential numerical instability issues, especially when dealing with high-dimensional inputs or complex scaling symmetries, would be important. Investigating the application of ScaleGMNs to other machine learning tasks and domains (like NLP or time series analysis) beyond INR processing is a promising avenue. Finally, exploring the synergy between scaling and other known NN symmetries, potentially leading to new inductive biases and improved model performance, deserves attention.

More visual insights

#

More on figures

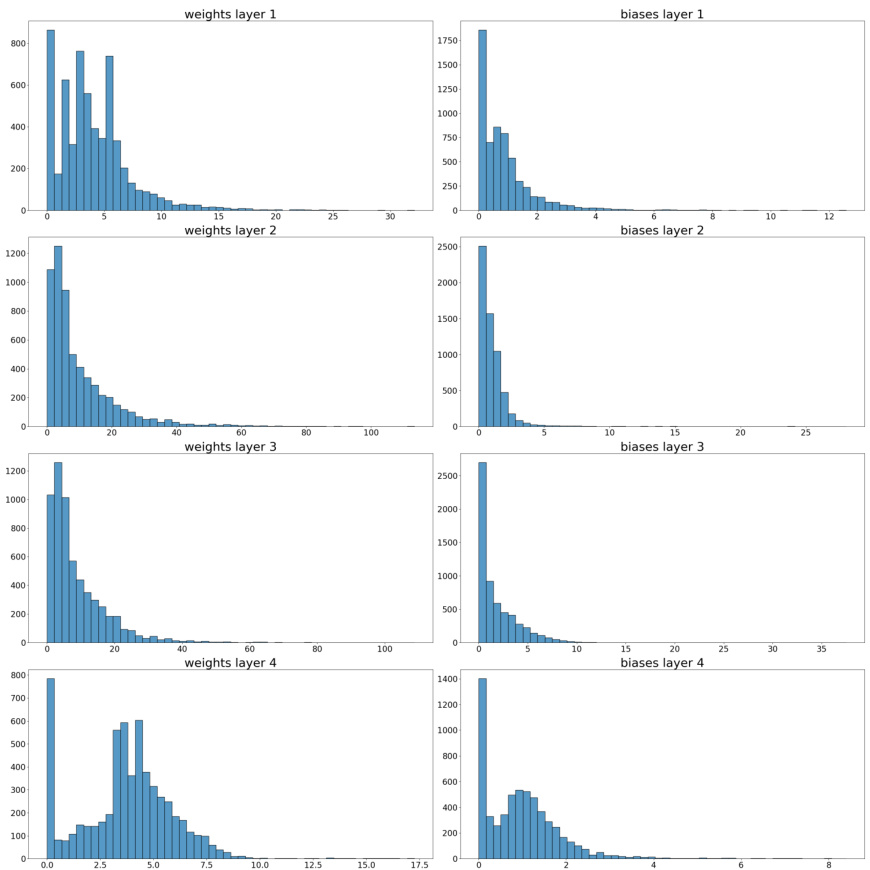
This figure shows the distribution of the norms of weights and biases for each layer (1-4) of a convolutional neural network trained on the CIFAR-10 dataset using ReLU activation function. The distributions are shown separately for weights and biases, providing a visual representation of how the magnitude of these parameters vary across the layers of the network. This information is relevant to understanding the scaling symmetries of neural networks and how they may affect learning and generalization.

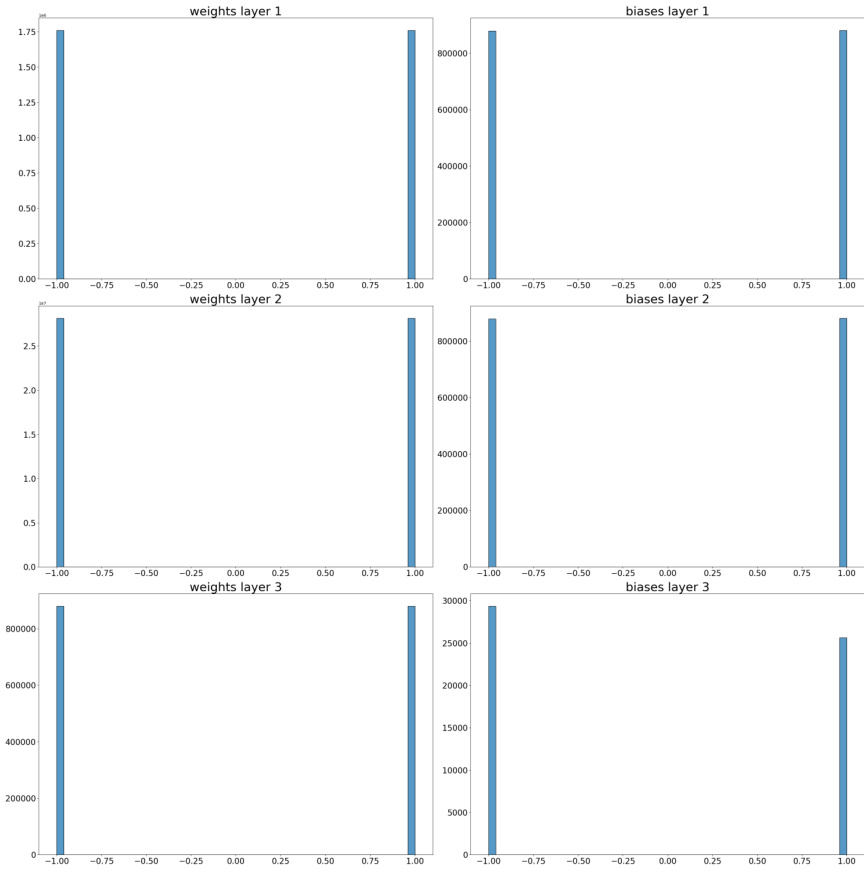
This figure shows the distribution of signs (+1 or -1) for weights and biases across four layers (layer 1 to layer 4) in the CIFAR-10-GS-tanh dataset. The histograms illustrate the proportion of positive and negative values for each layer, providing insights into the symmetry characteristics of the weights and biases in this dataset. Notably, the near-even distribution of positive and negative values in each layer suggests that the weights and biases do not have an inherent positive or negative bias, which is useful information for network training and analysis. The distributions also show the degree of symmetry, as an almost uniform distribution of weights/biases could suggest a high degree of symmetry.

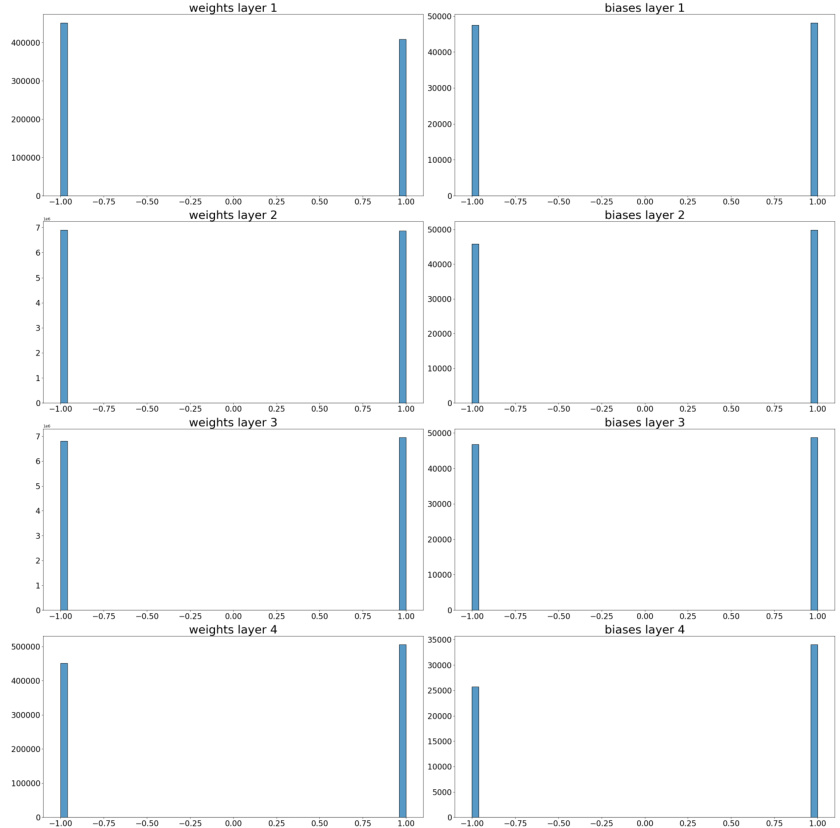
This figure shows the distribution of the norms of weights and biases for each layer of a convolutional neural network (CNN) trained on the CIFAR-10 dataset using ReLU activation functions. The distributions are shown separately for weights and biases, and are displayed for each layer of the network. The purpose of the figure is to illustrate the distribution of the parameters to showcase the need for Scale Equivariant networks. The distributions reveal variations across layers and whether the symmetries studied in this paper are present in the datasets used.

More on tables

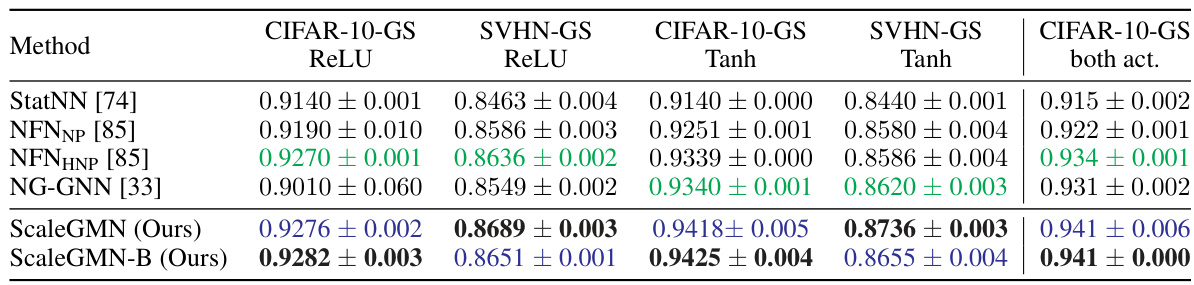
This table presents the Kendall-τ correlation results for generalisation prediction on subsets of the SmallCNN Zoo dataset. The results are broken down by activation function (ReLU or Tanh) and dataset (CIFAR-10-GS or SVHN-GS). The table compares the performance of ScaleGMN and ScaleGMN-B against various baseline methods. Higher Kendall-τ scores indicate better performance in predicting the generalization ability of the CNNs.

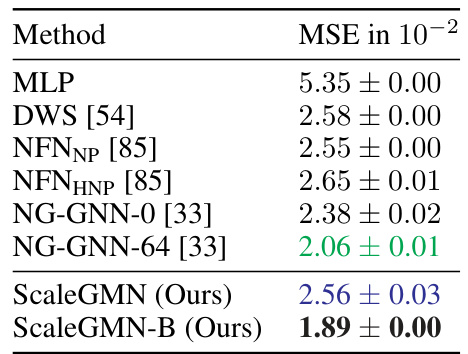
This table presents the Mean Squared Error (MSE) results for the task of dilating MNIST INRs (Implicit Neural Representations). It compares the performance of several methods, including a simple Multilayer Perceptron (MLP), and several state-of-the-art metanetworks such as DWS [54], NFNNP/NFNHNP [85], NG-GNN [33] and the proposed ScaleGMN and ScaleGMN-B. Lower MSE values indicate better performance in reconstructing the dilated images.

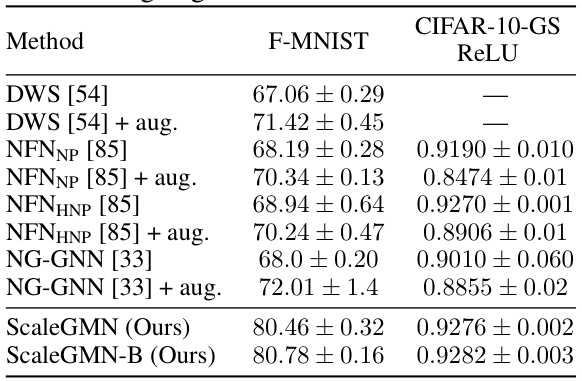
The table presents the results of INR classification experiments on four datasets: MNIST, F-MNIST, CIFAR-10, and Augmented CIFAR-10. Multiple methods, including the proposed ScaleGMN and several baselines, are evaluated based on their mean and standard deviation of accuracy across three different random seeds. The table highlights the superior performance of ScaleGMN, especially in comparison to other state-of-the-art methods.

Full paper

#