↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Clustering under Gaussian Mixture Models (GMMs) is a fundamental task in machine learning and statistics. Traditional methods often assume isotropic (equal) covariance matrices for all clusters, which is rarely true in real-world data. This simplification limits accuracy and applicability of existing algorithms. Anisotropic GMMs, where clusters have different covariance matrices, present a more realistic and challenging clustering problem. Existing approaches often struggle with the computational complexity of handling varying covariances, and theoretical guarantees are lacking.
This paper addresses these challenges by introducing two novel, computationally efficient clustering algorithms specifically designed for anisotropic GMMs. The algorithms iteratively estimate and utilize covariance information, resulting in significantly improved clustering accuracy compared to existing methods. The authors rigorously prove that their algorithms achieve minimax optimality—meaning they achieve the best possible accuracy—and converge quickly. The findings are supported by both theoretical analysis and numerical experiments demonstrating practical effectiveness.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in clustering and machine learning due to its novel algorithms that significantly improve clustering accuracy, especially in complex, real-world datasets. The minimax optimal rates and logarithmic convergence guarantees offer both theoretical significance and practical advantages. It opens new avenues for research, particularly concerning high-dimensional data and ill-conditioned covariance matrices. These advancements could lead to more effective solutions for various applications dealing with cluster analysis.
Visual Insights#

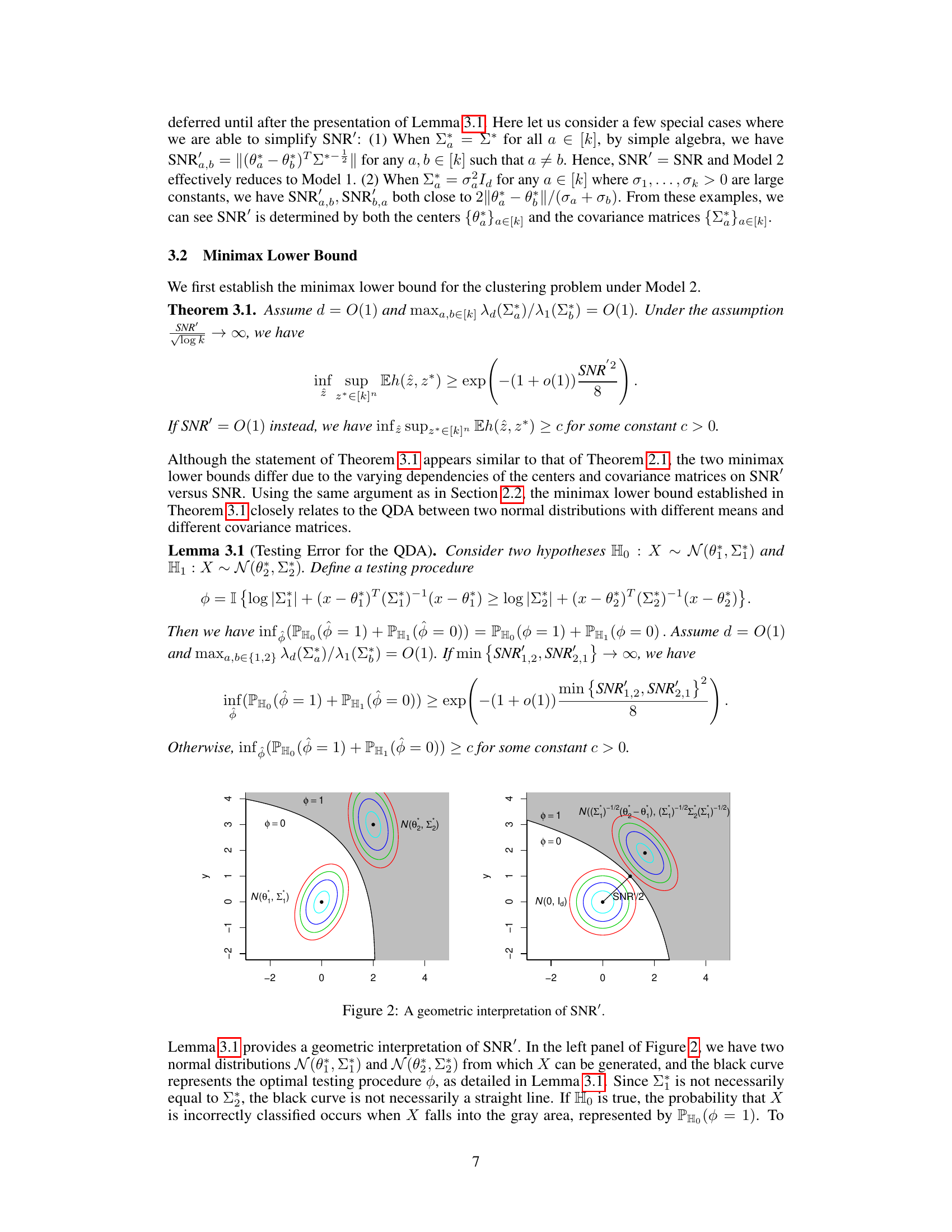
The figure provides a geometric interpretation of the signal-to-noise ratio (SNR) in the context of clustering under Gaussian Mixture Models (GMMs) with anisotropic covariance structures. The left panel shows two Gaussian distributions with different means and the same covariance matrix. The black line represents the optimal testing procedure that divides the space into two half-spaces. The right panel shows the same two distributions but with a transformation that makes them isotropic. The distance between the centers of the two distributions is shown, which is related to the SNR. This transformation helps visualize how the SNR captures the difficulty of clustering due to the separation of the cluster centers and the covariance structure.
In-depth insights#
Anisotropic GMMs#
Anisotropic Gaussian Mixture Models (GMMs) present a significant challenge in clustering compared to their isotropic counterparts. The anisotropy, stemming from non-spherical covariance matrices, fundamentally alters the geometric relationships between data points and cluster centers. This complexity necessitates novel algorithmic approaches that move beyond simple distance metrics. Successfully handling anisotropic GMMs requires accurate estimation of covariance matrices which, if not handled effectively, can significantly impact the clustering results. Furthermore, the minimax lower bounds for clustering accuracy under anisotropic GMMs demonstrate a critical dependence on the structure of the covariance matrices. Theoretical guarantees and practical efficiency become intertwined, as algorithms must not only achieve optimality but also converge efficiently, bridging the gap between theoretical understanding and practical implementation.
Minimax Rates#
The concept of “Minimax Rates” in the context of clustering under Gaussian Mixture Models (GMMs) centers on identifying the optimal theoretical performance limits. It establishes lower bounds on the achievable error rate for any clustering algorithm, regardless of its specific design. Crucially, this analysis considers the worst-case scenario across all possible data distributions within the specified GMM model. The minimax rate reveals the fundamental difficulty of the clustering problem, demonstrating the impact of factors such as the separation between cluster means (signal) and the covariance structures (noise). Anisotropic GMMs, where covariance matrices are not necessarily identity matrices, pose unique challenges. The minimax rate in such settings is shown to depend critically on the interplay between cluster means and covariance structure, which is more complex than the isotropic case where covariances are identical. Ultimately, the minimax rate serves as a benchmark for evaluating the performance of practical clustering algorithms, highlighting whether an algorithm achieves optimal theoretical accuracy. Achieving this optimality is a significant goal, as it represents a fundamental limit on performance given the statistical model assumptions.
Lloyd’s Algorithm#
Lloyd’s algorithm, a foundational iterative method in clustering, aims to partition data points into groups by iteratively refining cluster centroids. Its simplicity and effectiveness have led to widespread adoption. However, its original formulation assumes isotropic Gaussian Mixture Models (GMMs), meaning clusters have spherical covariance structures. This paper extends Lloyd’s algorithm to handle anisotropic GMMs, where clusters exhibit elliptical covariance structures. This extension is crucial as real-world data often deviates significantly from the isotropic assumption. The paper presents variations of the algorithm that estimate and iteratively utilize covariance information, bridging the gap between theoretical guarantees and practical efficiency. The modified algorithms achieve minimax optimality, meaning they reach the best possible accuracy given the data’s complexity and noise levels. The incorporation of covariance structure significantly enhances clustering accuracy, particularly when dealing with high-dimensional data or datasets with varying cluster shapes and densities. While computationally more expensive than the original Lloyd’s algorithm, the improvement in accuracy justifies the added cost, especially when dealing with more complex data structures. The paper provides rigorous theoretical analysis demonstrating the algorithm’s convergence and optimality, along with empirical evaluations showcasing its effectiveness on both synthetic and real-world data sets.
Computational efficiency#
The research paper analyzes the computational efficiency of its proposed clustering algorithm, comparing it to existing methods like Lloyd’s algorithm and spectral clustering. A key finding is that the new algorithm achieves rate-optimality, matching the theoretical lower bound for clustering accuracy under anisotropic Gaussian Mixture Models (GMMs). This optimality is achieved within a logarithmic number of iterations, making it practically efficient. However, the paper also acknowledges a trade-off. While achieving the optimal rate, the algorithm’s complexity increases due to the iterative estimation of covariance matrices, scaling as O(nkd³T) compared to Lloyd’s O(nkdT). The paper suggests further research to explore how to reduce this added computational cost, particularly in high-dimensional settings where the cubic dependence on d becomes significant. Overall, the efficiency analysis demonstrates a balance between theoretical optimality and practical feasibility, highlighting the potential of the algorithm but also pointing towards future improvements.
Future works#
The paper’s ‘Future Work’ section would ideally explore extending the adjusted Lloyd’s algorithm to high-dimensional settings (d>n), currently a limitation. Addressing ill-conditioned covariance matrices is crucial, perhaps by investigating robust estimation techniques or alternative algorithmic approaches. Theoretical analysis could be deepened to relax assumptions, such as the well-conditioned covariance matrices. A detailed investigation of the algorithm’s sensitivity to initialization is needed, potentially exploring adaptive or data-driven initialization methods. Empirical evaluation on a broader range of real-world datasets with varied characteristics and dimensions would strengthen the paper’s findings. Finally, comparing the proposed algorithm against a wider array of existing clustering methods, especially those tailored for anisotropic data, would provide a more thorough assessment of its relative performance and potential advantages.
More visual insights#
More on figures

The figure provides a geometric interpretation of the signal-to-noise ratio (SNR) used in the paper. The left panel shows two Gaussian distributions with different means but the same covariance matrix. The black curve represents the optimal testing procedure that separates the two distributions. The right panel shows the same distributions after a linear transformation that makes them isotropic (variance is equal in all directions). The distance between the transformed means in the right panel represents SNR. The closer the transformed means are, the harder it is to distinguish them (lower SNR, more difficult clustering).

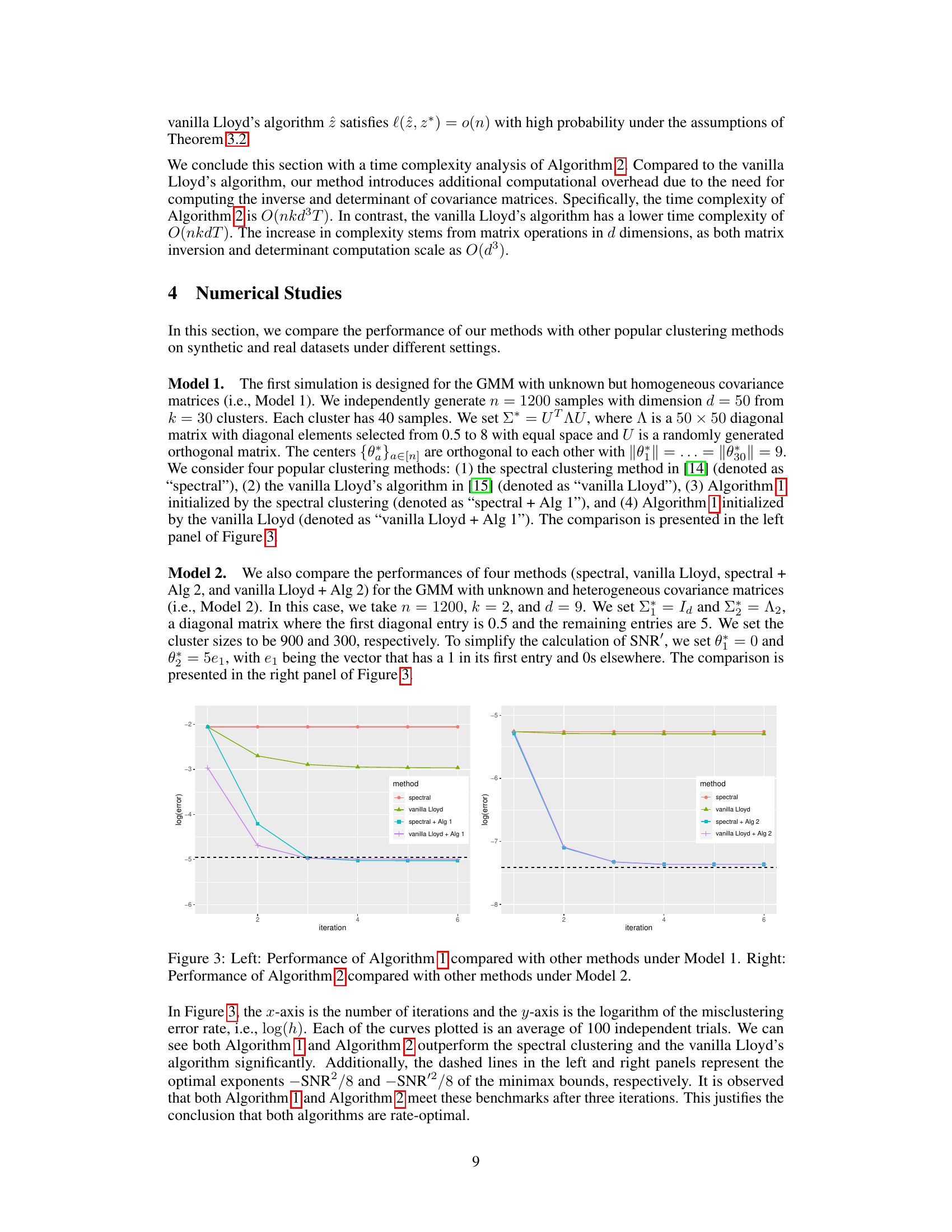
This figure compares the performance of the proposed algorithms (Algorithm 1 and Algorithm 2) with other baseline methods (spectral clustering and vanilla Lloyd’s algorithm) under two different anisotropic Gaussian Mixture Models (Model 1 and Model 2). The x-axis represents the number of iterations, while the y-axis shows the logarithm of the misclustering error rate. The plots visualize how the error rate decreases with increasing iterations for each method. The dashed black line represents the theoretical minimax lower bound for the error rate. The results illustrate that the proposed algorithms significantly outperform the baseline methods and achieve the optimal rate predicted by the minimax bounds.

This figure visualizes the Fashion-MNIST dataset using principal component analysis (PCA) to reduce dimensionality. The left panel shows two classes (T-shirt/top and Trouser), while the right panel includes a third (Ankle boot). The data points are color-coded by class, revealing the anisotropic and heterogeneous covariance structures (meaning the data’s spread and orientation vary across classes). This visualization supports the paper’s claim that the proposed clustering methods are suitable for handling such data characteristics.
Full paper#