↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Estimating physical properties from visual data is crucial for many applications like robotics and digital twins. However, existing methods often struggle with inaccurate geometry and appearance distortions during deformation. Many methods also assume elastic materials which limits their generalizability.
The GIC framework overcomes these challenges by combining the strengths of 3D Gaussian representation for accurate geometry and a continuum simulation for capturing dynamic behavior. By incorporating 2D shape guidance from rendered object masks, GIC improves estimation accuracy and robustness, outperforming previous approaches across several benchmarks. This work significantly advances research into visual system identification with its practical and accurate approach.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel hybrid framework for estimating physical properties from visual observations, achieving state-of-the-art results. Its geometry-aware approach, using 3D Gaussian representation and a Gaussian-informed continuum, addresses limitations of existing methods. This opens avenues for research in digital twins, robotics, and other applications needing accurate property estimation from visual data. The real-world demonstrations showcase its practical utility, increasing its relevance to various fields.
Visual Insights#
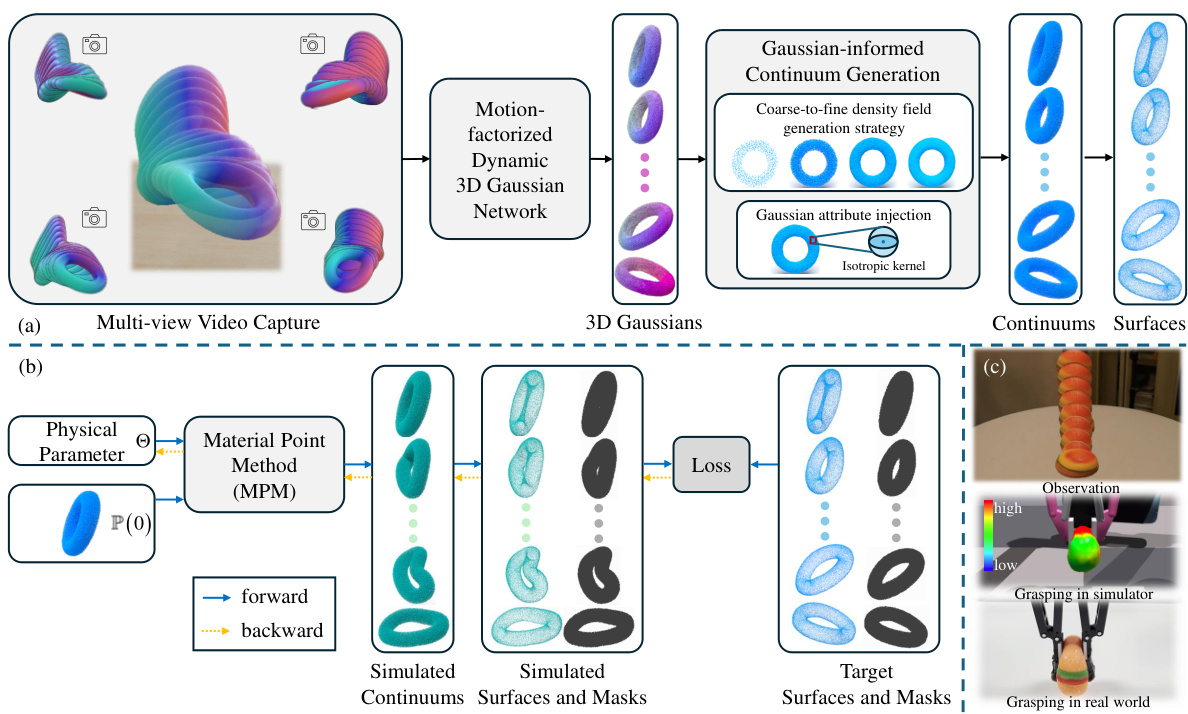
This figure provides a high-level overview of the proposed pipeline, which consists of three main modules: Continuum Generation, Identification, and Simulation. The Continuum Generation module uses a motion-factorized dynamic 3D Gaussian network to reconstruct the object’s shape over time from multiple views and generates a continuum representation. The Identification module uses Material Point Method (MPM) simulation to estimate physical properties by comparing simulated and observed object shapes and masks. Finally, the Simulation module demonstrates the use of the estimated properties for realistic object behavior simulation, particularly showcasing a digital twin application in robotic grasping.
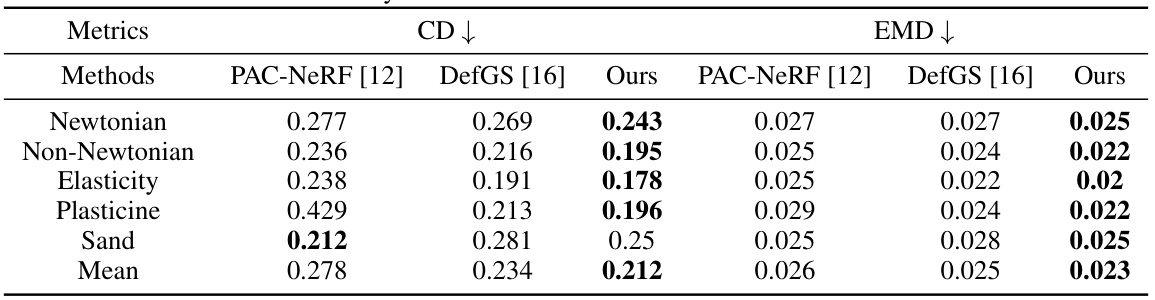
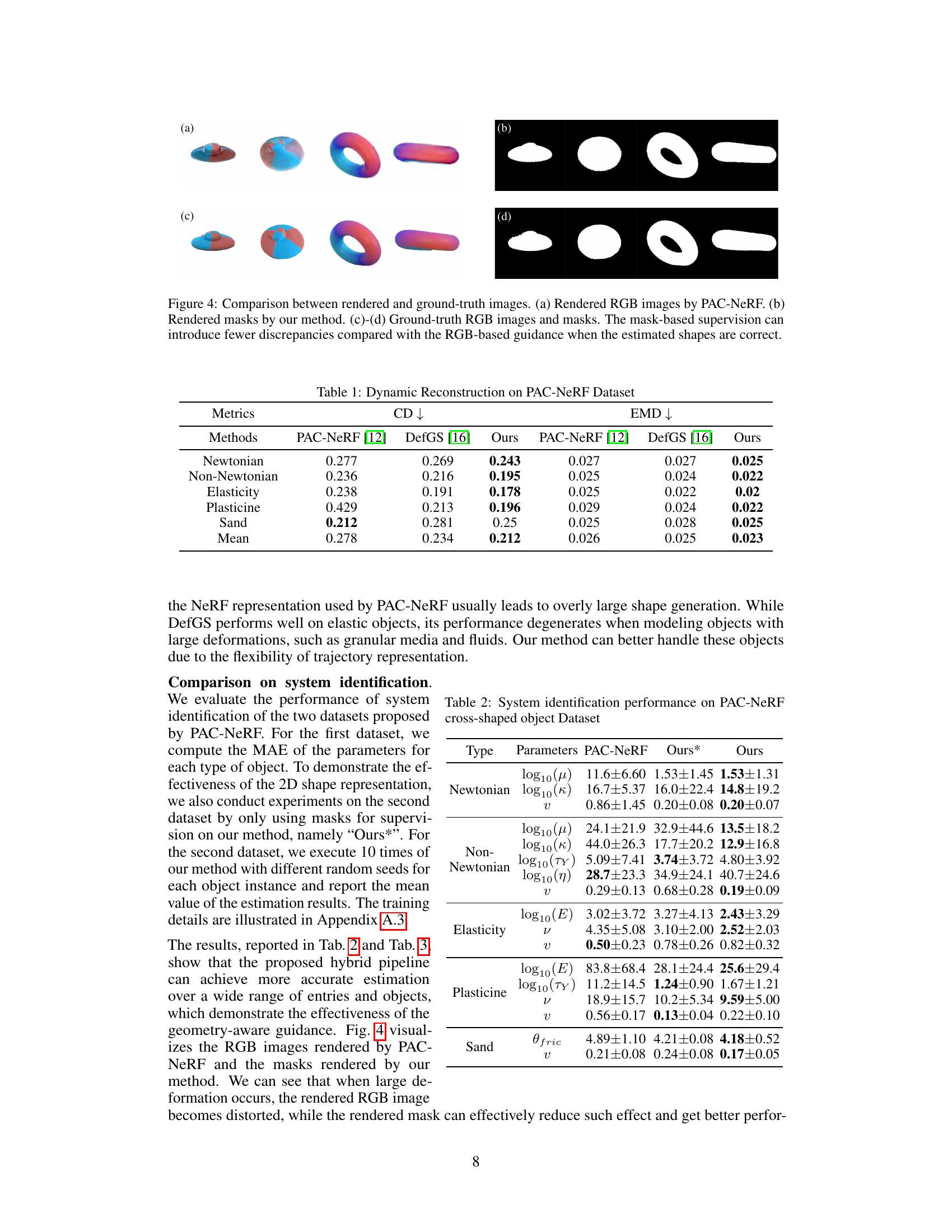
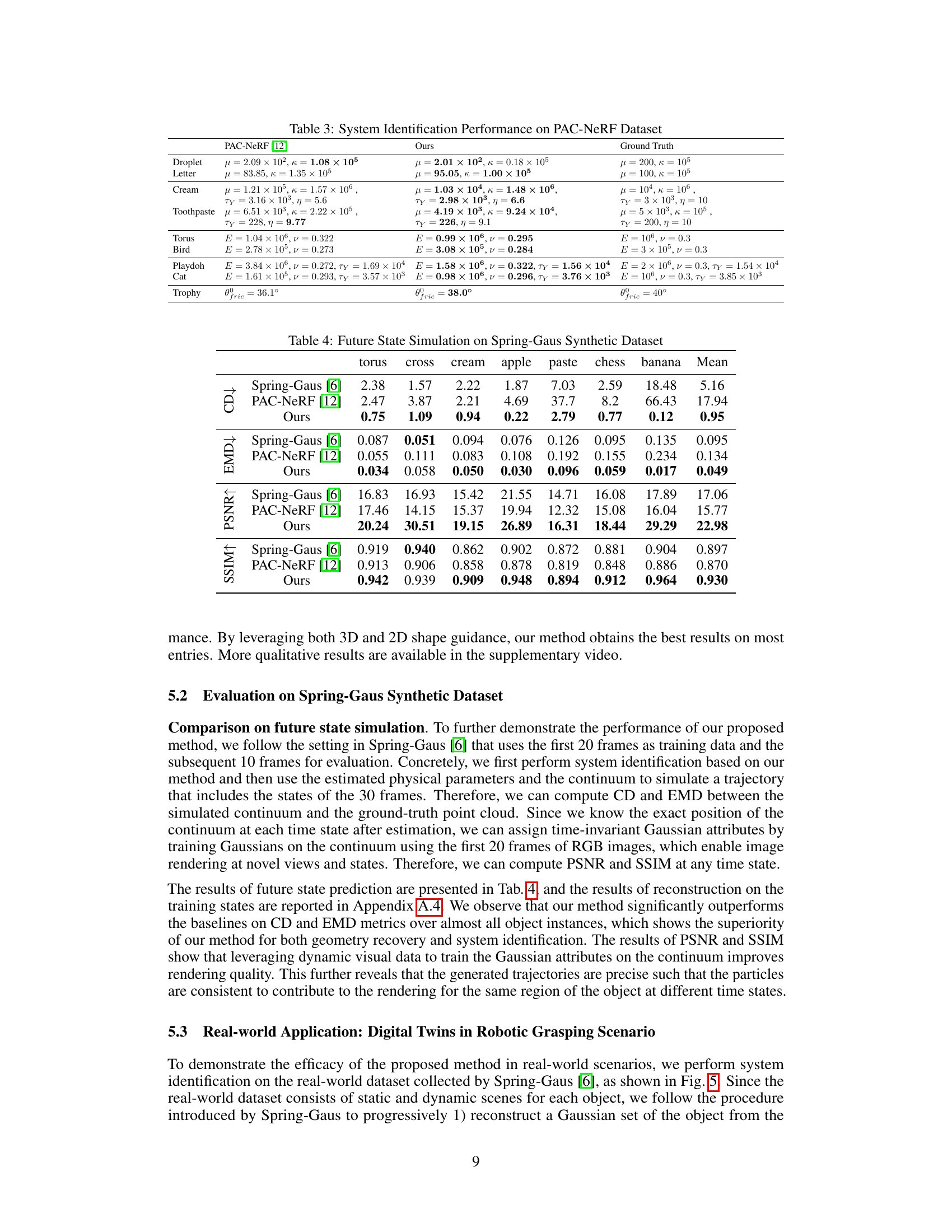
This table presents a comparison of dynamic reconstruction performance on the PAC-NeRF dataset across three different methods: PAC-NeRF, DefGS, and the proposed method (Ours). The metrics used for comparison are Chamfer Distance (CD) and Earth Mover’s Distance (EMD), both measuring the discrepancy between the reconstructed and ground truth shapes. Lower values indicate better performance. The results are broken down by material type (Newtonian, Non-Newtonian, Elasticity, Plasticine, Sand) and provide a mean across all material types.
In-depth insights#
Gaussian Scene Capture#
A hypothetical ‘Gaussian Scene Capture’ heading in a research paper likely involves representing a 3D scene using a collection of 3D Gaussian distributions. This approach offers several advantages. First, Gaussian distributions naturally encode uncertainty, reflecting the inherent ambiguity in real-world scene perception. Second, Gaussians are computationally efficient, allowing for faster rendering and manipulation compared to other dense scene representations. Third, Gaussians can easily be integrated with physically-based simulation techniques, making them suitable for tasks involving dynamic scenes and object interactions. The specific implementation details would vary greatly, but may include techniques for efficient Gaussian fitting, methods for handling occlusion, and algorithms for generating novel views from the Gaussian representation. The choice of covariance matrices within each Gaussian is crucial, influencing the level of detail and uncertainty captured. A key challenge would be to balance the trade-off between computational efficiency and the accuracy of the scene representation.
Dynamic 3D Gaussians#
Dynamic 3D Gaussian methods represent a significant advancement in 3D scene representation, particularly for dynamic scenes. They leverage the efficiency and expressiveness of Gaussian distributions to model the position, scale, and potentially other attributes of points in 3D space. The “dynamic” aspect introduces temporal coherence, allowing for tracking of objects and their deformations over time. This approach offers several advantages: high-quality rendering with fewer artifacts, compact representation, and potential for integration with physical simulation methods. However, challenges exist in handling complex deformations and occlusion, as well as balancing the accuracy of the Gaussian representation against computational cost. Future developments could involve more sophisticated models of motion and deformation, improved strategies for handling large datasets, and exploration of applications in fields such as robotics and virtual reality.
Continuum Simulation#
Continuum simulation, in the context of this research paper, is a crucial aspect for estimating physical properties of objects from visual observations. The paper introduces a novel hybrid framework that leverages 3D Gaussian representation to capture both explicit shapes and enable continuum rendering for geometry-aware guidance. A key innovation is the dynamic 3D Gaussian framework that reconstructs the object across time, facilitating the extraction of object continuums along with their surfaces. This is achieved through a coarse-to-fine filling strategy, generating density fields to sample continuum particles for accurate simulation. The integration of Gaussian attributes into these continuums further enhances the simulation’s accuracy. The Gaussian-informed continuum renders object masks during simulation, providing additional 2D shape guidance for improved physical property estimation, ultimately achieving state-of-the-art performance.
Property Estimation#
The paper centers around estimating physical properties, or “property estimation,” of objects using visual observations. A key challenge is geometry awareness, as accurate shape representation is crucial for precise property inference. The proposed method cleverly addresses this by combining 3D Gaussian shape representation with 2D shape surrogates (masks) during simulation. This hybrid approach leverages the strengths of both explicit 3D shape information and implicit 2D visual cues for robust estimation, overcoming limitations of prior methods that relied solely on implicit or noisy geometry reconstruction. The Gaussian-informed continuum is a particularly innovative aspect, integrating Gaussian attributes directly into a simulated continuum, enabling mask rendering that aids in parameter estimation. The process goes from coarse-to-fine density field generation, progressively refining the shape for both accurate 3D representation and reliable 2D mask supervision, demonstrating state-of-the-art performance across multiple benchmarks. Thus, the research presents a novel and effective framework for geometry-aware physical property estimation from visual data.
Real-world Use Case#
A compelling ‘Real-world Use Case’ section would showcase the practical applicability of the Gaussian-Informed Continuum (GIC) framework. It should go beyond simple demonstrations and delve into a specific application where the system’s ability to identify physical properties from visual observation offers a clear advantage. A strong example could involve robotic manipulation, showcasing how GIC enables a robot to grasp and interact with deformable objects of varying materials more effectively. The section must highlight the accuracy and efficiency gains of GIC compared to existing methods in a real-world context, perhaps quantifying these gains with metrics relevant to the chosen application. Including a detailed description of the experimental setup, including the object types, camera setup, and performance metrics, would significantly enhance the credibility. Ideally, the narrative should flow naturally from the theoretical aspects of the paper to its concrete impact on a real-world problem, demonstrating the value proposition of the GIC framework in a tangible way.
More visual insights#
More on figures
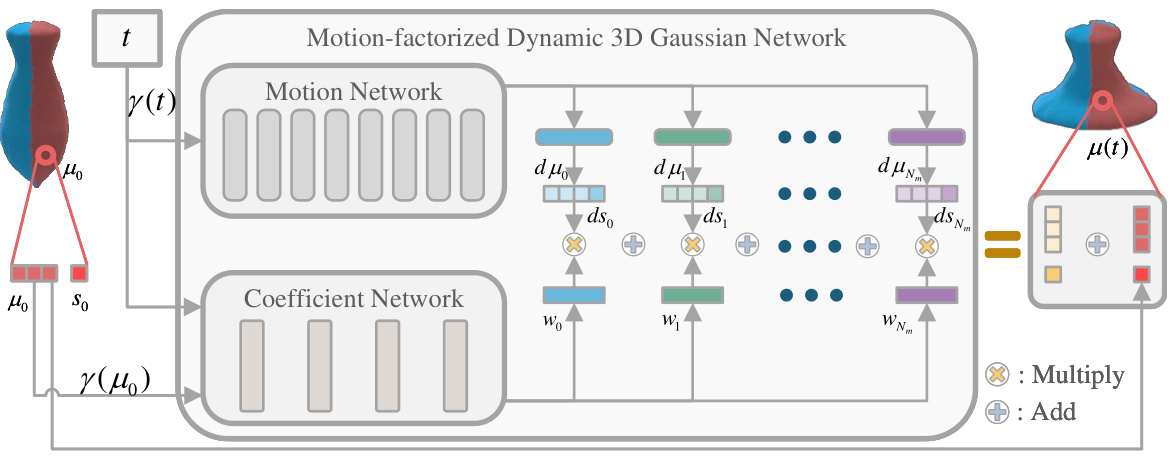
This figure illustrates the architecture of the dynamic 3D Gaussian network, a key component of the proposed method. It shows how the network processes input data (time and initial Gaussian parameters) to generate updated Gaussian parameters for dynamic scene reconstruction. The network is composed of two main parts: a motion network and a coefficient network. The motion network decomposes the object’s motion into multiple motion bases, and the coefficient network maps canonical positions and time to corresponding motion coefficients. These components are combined to produce updated Gaussian parameters for each point in the object at each time step, enabling accurate and efficient dynamic scene reconstruction.
This figure provides a high-level overview of the proposed pipeline for physical property identification and simulation. It shows three main stages: (a) Continuum Generation: Reconstruction of a dynamic object from multiple views using a motion-factorized dynamic 3D Gaussian network, generating density fields, and extracting surfaces. Gaussian attributes are added for mask rendering during simulation. (b) Identification: MPM simulation using the initial continuum and physical parameters, comparing simulated results (surfaces and masks) to extracted ground truth for parameter estimation. (c) Simulation: Illustrative simulation results of the digital twin showing behavior consistent with real-world objects.

This figure provides a high-level overview of the proposed pipeline for physical property identification and simulation. It shows three main stages: 1) Continuum generation: reconstructing the object’s shape and generating a continuum representation using a motion-factorized dynamic 3D Gaussian network and a coarse-to-fine filling strategy. 2) Identification: using the Material Point Method (MPM) to simulate the object’s motion and comparing it to the observations to estimate physical parameters. 3) Simulation: showcasing the ability of the pipeline to simulate realistic object behavior based on the estimated parameters. The figure is divided into three subfigures to illustrate these three steps.

This figure provides a high-level overview of the proposed pipeline for physical property identification and simulation using Gaussian-informed continuums. It shows three main modules: continuum generation from multi-view images using a motion-factorized dynamic 3D Gaussian network; physical property identification by comparing simulated and observed object surfaces and masks; and simulation demonstrating the effectiveness of the estimated properties in a digital twin setting.

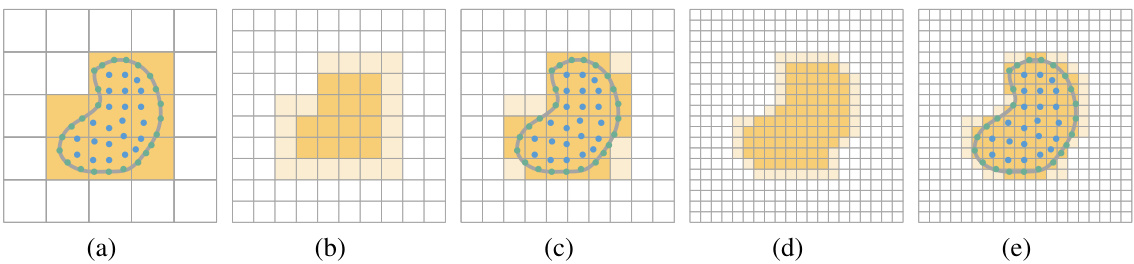
This figure shows a comparison of the coarse-to-fine filling strategy used in the proposed method with different numbers of upsampling steps (a-d), along with the results from PAC-NeRF (e) and the ground truth shapes (f). The images visually demonstrate how the iterative upsampling and smoothing operations refine the density field, resulting in more accurate shape representations compared to PAC-NeRF, which tends to recover overly large shapes.

This figure provides a high-level overview of the proposed pipeline for physical property identification and simulation. It illustrates the three main modules: continuum generation using a motion-factorized dynamic 3D Gaussian network, physical property identification by comparing simulated and observed object shapes and masks, and simulation for digital twin demonstrations. The process starts with multi-view video capture, then proceeds to continuum generation, physical parameter identification and finally simulation with the estimated parameters.

This figure shows a real-world application of the proposed method. The left side demonstrates the identification and future state simulation, where the object’s physical properties are first identified, and then used to simulate its future behavior. The right side depicts a robotic grasping simulation, showing how the estimated properties and simulation results are used to perform realistic grasps with different gripper widths (6cm, 4.5cm, and 3.5cm). The color of the simulated object indicates the stress level, with blue representing low stress and red representing high stress.
More on tables
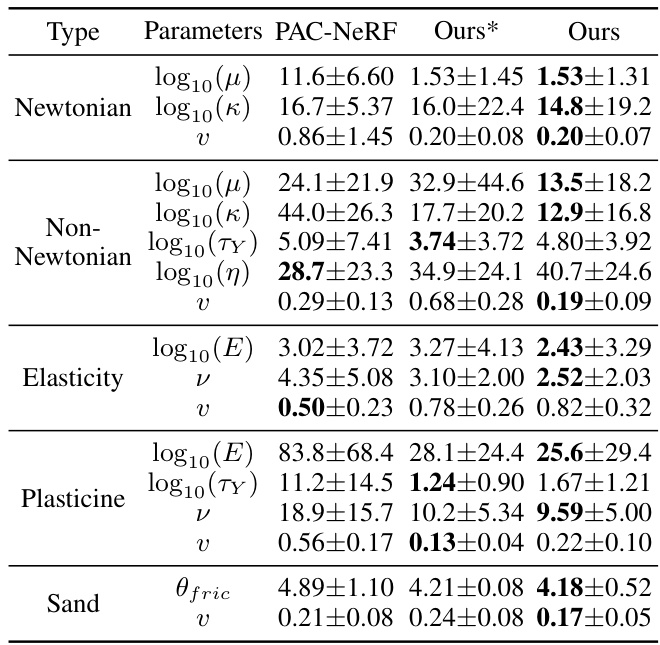
This table presents the quantitative results of dynamic reconstruction experiments performed on the PAC-NeRF dataset. It compares the performance of three different methods: PAC-NeRF, DefGS, and the proposed method (‘Ours’). The evaluation metrics used are Chamfer Distance (CD) and Earth Mover’s Distance (EMD), which measure the discrepancy between the reconstructed shapes and the ground truth shapes. Results are provided for various object types, including Newtonian, Non-Newtonian fluids, elastic, plasticine, and sand, showing the overall performance and the performance breakdown by material type.

This table presents a comparison of dynamic reconstruction performance on the PAC-NeRF dataset. Three methods are compared: PAC-NeRF [12], DefGS [16], and the proposed method. The evaluation metrics are Chamfer Distance (CD) and Earth Mover’s Distance (EMD), both measuring the discrepancy between reconstructed and ground truth shapes. The results are broken down by material type (Newtonian, Non-Newtonian, Elasticity, Plasticine, Sand), providing a comprehensive view of each method’s strengths and weaknesses across different material properties.
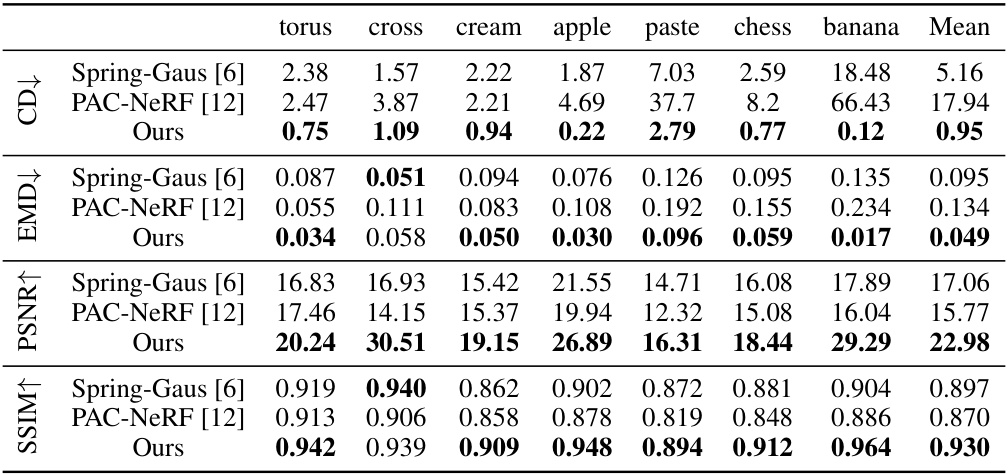
This table presents a comparison of dynamic reconstruction performance on the PAC-NeRF dataset, comparing three different methods: PAC-NeRF, DefGS, and the proposed method. The comparison uses Chamfer Distance (CD) and Earth Mover’s Distance (EMD) metrics across different material types (Newtonian, Non-Newtonian, Elasticity, Plasticine, and Sand). Lower values indicate better performance.
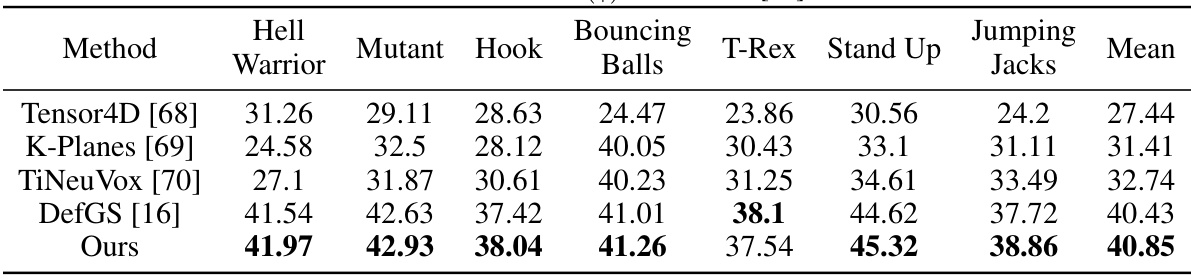
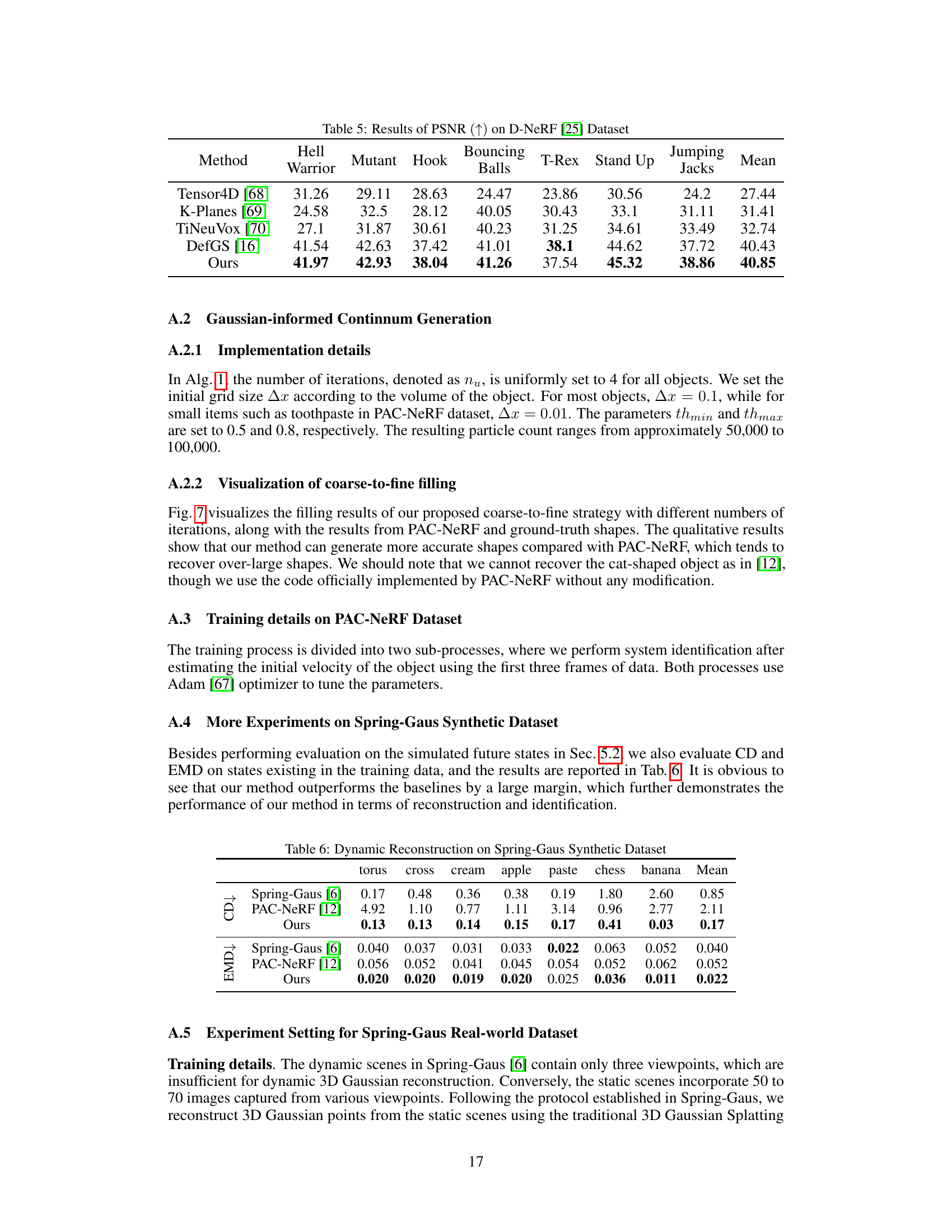
This table presents a comparison of the Peak Signal-to-Noise Ratio (PSNR) achieved by different methods on the D-NeRF dataset for novel view synthesis. The PSNR values are shown for each scene and method, with higher PSNR indicating better image quality. The methods compared include Tensor4D, K-Planes, TiNeuVox, DefGS, and the proposed method ‘Ours’. The results demonstrate the superior performance of the proposed method in generating high-quality novel views.
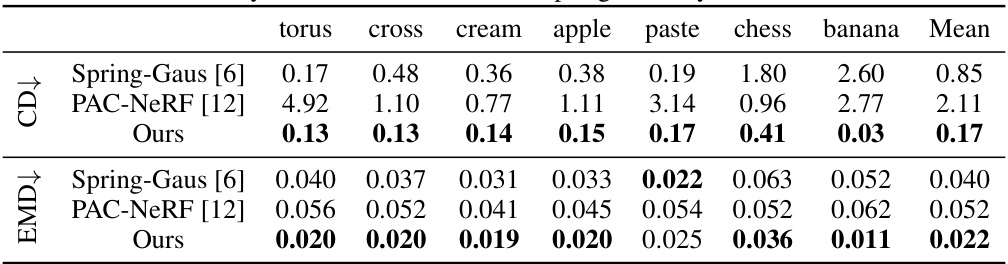
This table presents a comparison of dynamic reconstruction performance on the PAC-NeRF dataset. Three methods are compared: PAC-NeRF, DefGS, and the proposed method (Ours). The comparison uses two metrics: Chamfer Distance (CD) and Earth Mover’s Distance (EMD). Results are presented separately for Newtonian, Non-Newtonian, Elasticity, Plasticine, and Sand materials, along with an overall mean.
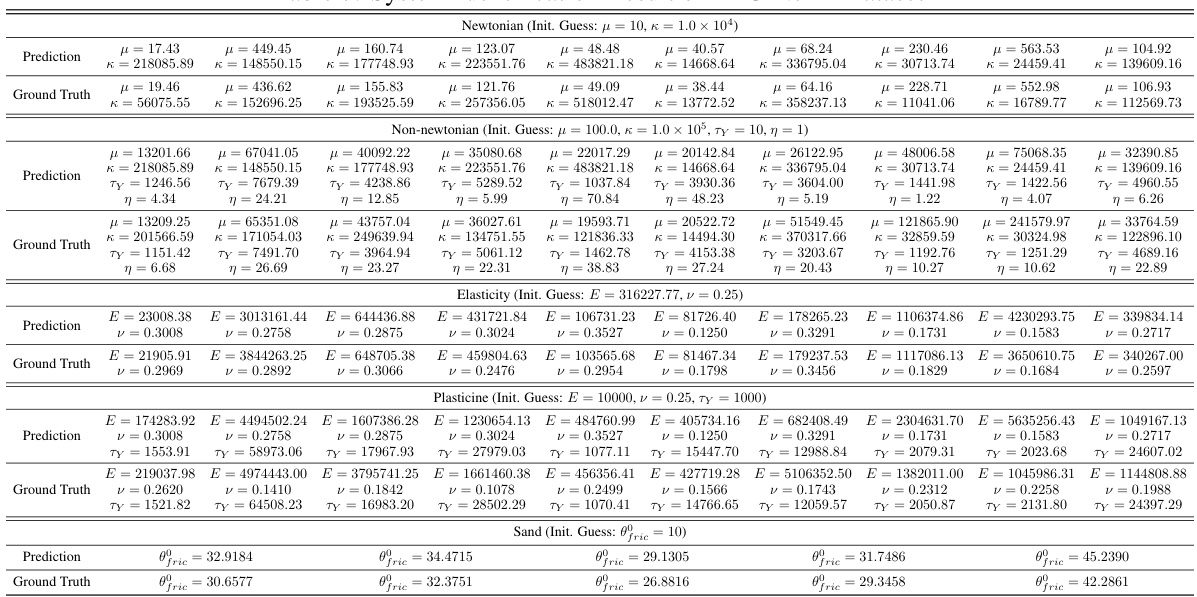
This table presents a comparison of the dynamic reconstruction performance of three different methods: PAC-NeRF, DefGS, and the proposed method, on the PAC-NeRF dataset. The comparison is made across different material types (Newtonian, Non-Newtonian, Elastic, Plasticine, Sand) using two metrics: Chamfer Distance (CD) and Earth Mover’s Distance (EMD). Lower values for CD and EMD indicate better reconstruction accuracy.

This table presents a quantitative comparison of dynamic reconstruction performance on the PAC-NeRF dataset. Three methods are compared: PAC-NeRF, DefGS, and the proposed method. The comparison is based on two metrics: Chamfer Distance (CD) and Earth Mover’s Distance (EMD). The results are broken down by material type (Newtonian, Non-Newtonian, Elasticity, Plasticine, Sand) and provide a mean across all material types. Lower values of CD and EMD indicate better reconstruction accuracy.
This table presents a comparison of dynamic reconstruction performance on the PAC-NeRF dataset. Three methods are compared: PAC-NeRF, DefGS, and the proposed method (Ours). The metrics used for comparison are Chamfer Distance (CD) and Earth Mover’s Distance (EMD), both measuring the difference between the reconstructed and ground truth shapes. Results are shown for four material types: Newtonian, Non-Newtonian, Elastic, and Plasticine, along with an overall mean.
Full paper#