↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Federated Q-learning aims to collaboratively train a Q-function across multiple agents, minimizing both the amount of data needed (sample complexity) and communication overhead. However, there’s a trade-off: reducing one often increases the other. Existing intermittent communication algorithms offer suboptimal performance in either sample or communication complexity.
This work addresses this trade-off. It first establishes fundamental limits on communication complexity, proving that achieving linear speedup in sample complexity requires at least logarithmic communication cost. Then, it introduces Fed-DVR-Q, a novel algorithm that achieves both order-optimal sample and communication complexities, providing a complete characterization of this trade-off. This is the first algorithm to achieve this important milestone.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in federated learning and reinforcement learning. It provides a complete characterization of the sample-communication complexity trade-off in Federated Q-learning, a problem critical to the scalability and efficiency of decentralized RL systems. The order-optimal algorithm (Fed-DVR-Q) proposed opens avenues for designing practical and efficient federated RL algorithms, impacting various applications, and encouraging further research on communication-efficient distributed optimization.
Visual Insights#
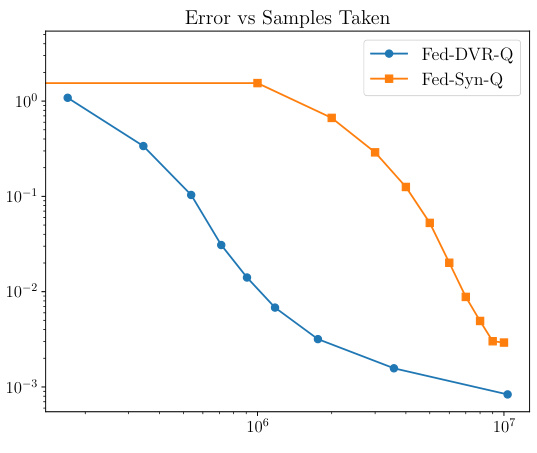
This figure compares the performance of the proposed Fed-DVR-Q algorithm and the Fed-SynQ algorithm from a previous work (Woo et al., 2023). It shows the error rate (y-axis) achieved by each algorithm against the number of samples used (x-axis). A second plot shows communication complexity (in bits) versus the number of samples used. Fed-DVR-Q demonstrates superior performance in terms of both accuracy and communication efficiency.
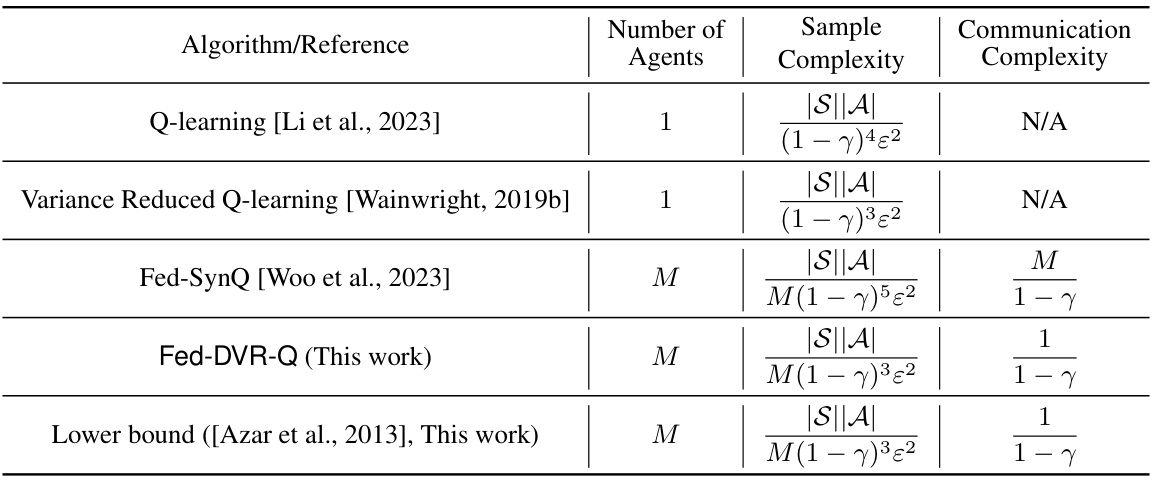
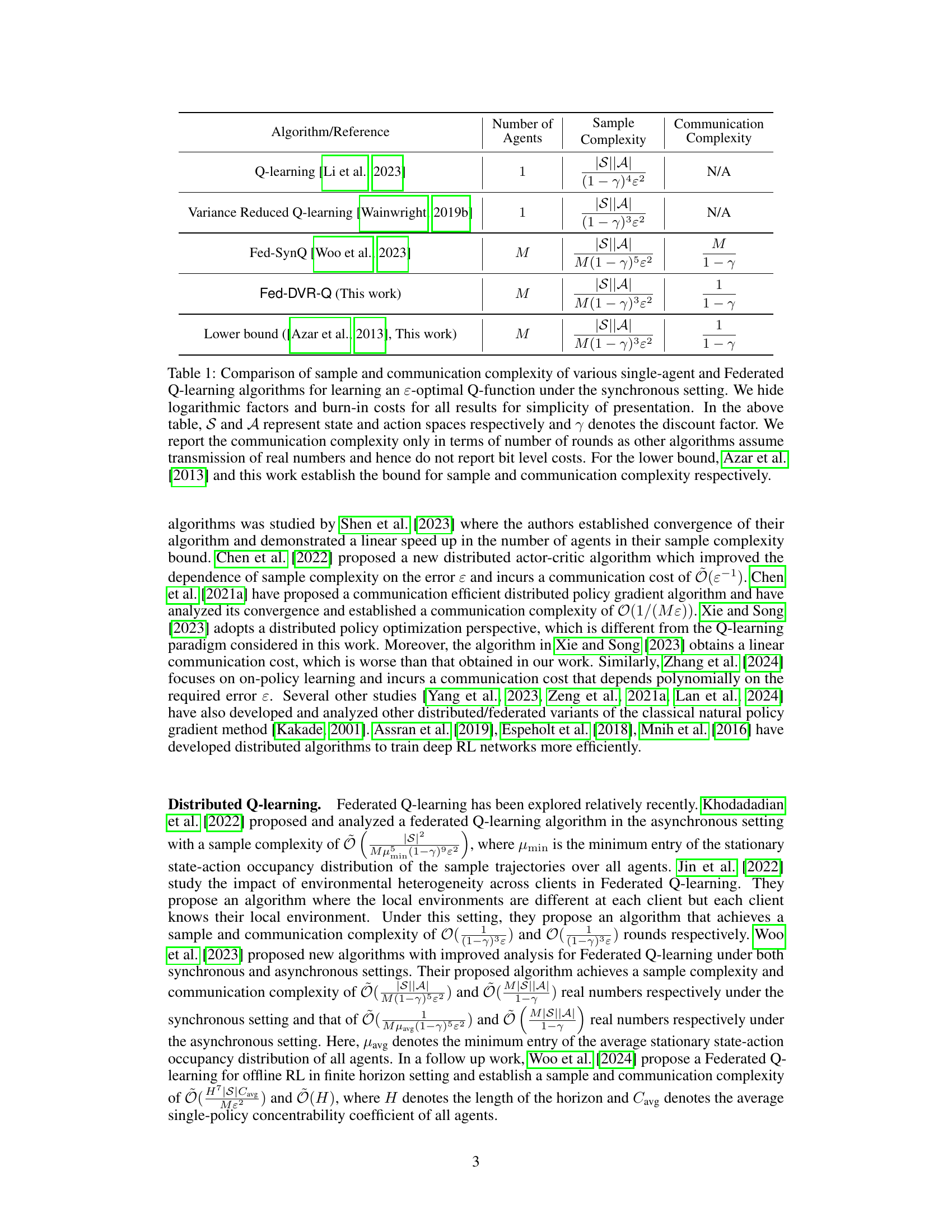
The table compares the sample and communication complexity of several single-agent and federated Q-learning algorithms. It shows the number of agents, the sample complexity (number of samples needed to learn an epsilon-optimal Q-function), and the communication complexity (number of communication rounds). Logarithmic factors and burn-in costs are omitted for simplicity. The table highlights that the proposed Fed-DVR-Q algorithm achieves optimal sample and communication complexity.
In-depth insights#
Fed-Learning Limits#
The heading ‘Fed-Learning Limits’ suggests an exploration of fundamental constraints in federated learning. A thoughtful analysis would delve into communication bottlenecks, examining the bandwidth limitations and latency issues inherent in distributed settings. It would also investigate data heterogeneity, addressing the challenges posed by inconsistent data distributions across participating clients. Moreover, privacy concerns represent a significant limit, requiring careful consideration of data anonymization and differential privacy techniques. Finally, model complexity and the computational resources required for model training on decentralized systems would be crucial aspects to consider. The limitations imposed by these factors ultimately determine the scalability and performance of federated learning systems, especially in resource-constrained environments.
Fed-DVR-Q Algorithm#
The proposed Fed-DVR-Q algorithm is a novel Federated Q-learning algorithm designed to address the sample-communication complexity trade-off. It achieves order-optimal sample complexity, meaning it requires a near-minimal number of samples to learn an effective Q-function, demonstrating a linear speedup with respect to the number of agents. Simultaneously, it attains the minimal communication complexity dictated by theoretical lower bounds, making it highly efficient in terms of communication rounds and bits transmitted. The algorithm’s core innovation lies in its combination of doubly variance reduction and minibatching techniques. Doubly variance reduction reduces the variance of Q-function updates, leading to faster convergence, while minibatching improves communication efficiency. The algorithm’s performance is theoretically guaranteed and is empirically validated through simulations, demonstrating improved performance over existing Federated Q-learning algorithms in terms of both sample and communication efficiency. Fed-DVR-Q represents a significant advancement in Federated Q-learning by achieving the optimal balance between sample and communication complexity, suggesting a practical and efficient approach for collaborative reinforcement learning in distributed settings.
Communication Tradeoffs#
The concept of communication tradeoffs in distributed machine learning, particularly in federated settings, is crucial. It explores the tension between the need for frequent communication to achieve fast convergence and the desire to minimize communication overhead for efficiency and scalability. Reducing communication complexity is paramount, especially in resource-constrained environments or when dealing with bandwidth limitations. The paper investigates this tradeoff within the context of Federated Q-learning. Strategies to reduce communication often involve techniques like compression, intermittent communication, or variance reduction. However, these methods may result in suboptimal sample complexity (requiring more data) to compensate for the loss in frequent information exchange. Finding the optimal balance between these complexities is a key challenge; achieving both minimal communication and optimal data efficiency is highly desirable but difficult. The paper contributes by analyzing this tradeoff, providing lower bounds on communication costs, and proposing a novel algorithm aiming to reach order-optimal sample and communication complexities simultaneously. This research highlights the importance of careful algorithm design to navigate the practical constraints of real-world federated learning.
Mini-Batching Effects#
Mini-batching, in the context of federated Q-learning, significantly impacts the algorithm’s performance. Smaller batch sizes increase the frequency of updates but introduce more noise, potentially slowing convergence due to higher variance. Conversely, larger batch sizes reduce the noise and can lead to faster convergence, but each update becomes more computationally expensive. The optimal batch size represents a trade-off between these two competing factors. The paper likely investigates how mini-batching interacts with the intermittent communication strategy, exploring whether the optimal batch size changes based on communication frequency. It also analyzes how mini-batching affects the bias-variance tradeoff within the federated setting, and potentially its effect on the communication complexity. The choice of batch size critically influences the algorithm’s sample and communication efficiency. The study’s findings would reveal valuable insights into designing efficient federated Q-learning algorithms by optimizing the batch size for different communication regimes and exploring its effects on overall convergence.
Future Research#
The paper’s conclusion suggests several avenues for future research, focusing on extending the current work’s scope. One key area is to move beyond the tabular setting and explore function approximation techniques for handling larger state and action spaces. This would make the algorithms more practical for real-world applications. Another interesting direction is to investigate the sample-communication trade-off in finite-horizon settings. This requires modifications to the core algorithms, as the discount factor plays a crucial role in the current analysis. A final suggestion for future work lies in exploring algorithms that go beyond the intermittent communication paradigm, potentially achieving even lower communication costs while maintaining optimal sample complexity. This would involve the design of fundamentally different distributed learning strategies.
More visual insights#
More on figures
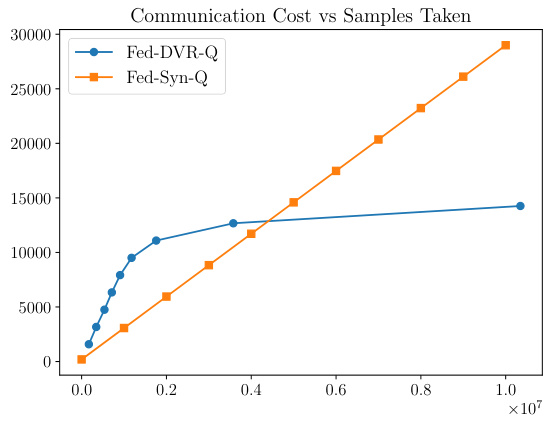
The figure compares the performance of the proposed Fed-DVR-Q algorithm with the Fed-SynQ algorithm from a prior work in terms of sample complexity and communication complexity. The sample complexity plots the error rate against the number of samples used, illustrating that Fed-DVR-Q achieves lower error rates for the same number of samples. The communication complexity plot shows the total bits transmitted against the number of samples, demonstrating that Fed-DVR-Q requires significantly less communication for comparable performance.
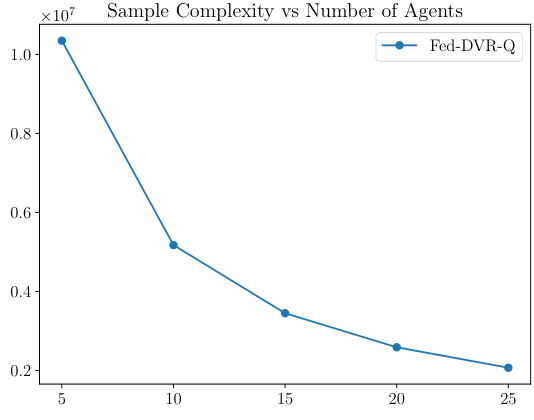
This figure shows how the sample and communication complexities of the Fed-DVR-Q algorithm change with the number of agents involved. The left panel (a) demonstrates that the sample complexity decreases linearly with the number of agents, indicating a linear speedup. The right panel (b) shows that the communication complexity remains relatively constant regardless of the number of agents. This confirms the theoretical findings of the paper, highlighting the algorithm’s efficiency in terms of communication overhead while maintaining optimal sample complexity.
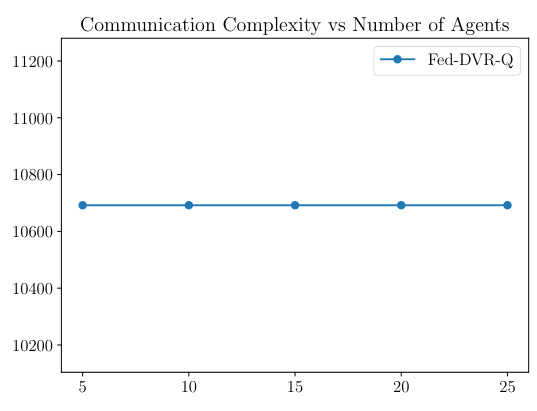
This figure shows how the sample and communication complexities of the Fed-DVR-Q algorithm change with the number of agents involved. The left subplot shows that the sample complexity decreases linearly with the number of agents (linear speedup), while the right subplot demonstrates that the communication complexity remains roughly constant, independent of the number of agents. This highlights the efficiency of the algorithm in terms of communication, even as it scales to handle more agents.
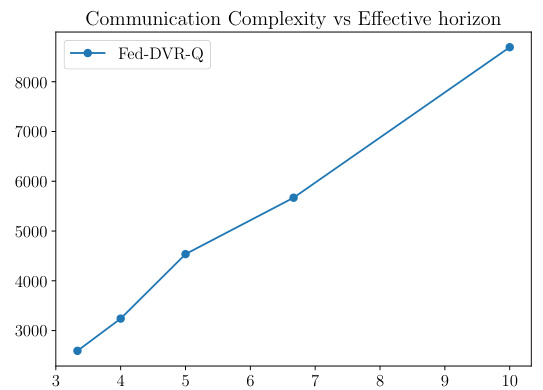
This figure shows how the communication complexity of the Fed-DVR-Q algorithm scales with the effective horizon, which is defined as 1/(1-γ), where γ is the discount factor. The plot demonstrates a linear relationship between communication complexity and effective horizon, corroborating the theoretical findings presented in the paper.
More on tables

This table compares the sample and communication complexity of several single-agent and federated Q-learning algorithms, highlighting the trade-off between these two factors. It considers the synchronous setting and shows that Fed-DVR-Q, a new algorithm proposed in this paper, achieves optimal order sample and communication complexity. The table hides logarithmic factors for simplicity.

The table compares the sample and communication complexity of several single-agent and federated Q-learning algorithms. It highlights the trade-off between sample complexity (number of samples needed to achieve a certain accuracy) and communication complexity (communication cost required to achieve the same accuracy). The algorithms are evaluated under a synchronous setting (all agents update simultaneously), and logarithmic factors and burn-in costs are omitted for simplicity. The communication complexity is expressed in terms of communication rounds, due to variations in how other works report communication cost (some report number of bits). Finally, the table includes a lower bound for both sample and communication complexity.

This table compares the sample and communication complexity of several single-agent and federated Q-learning algorithms. It shows the number of agents, the sample complexity (number of samples needed to learn an epsilon-optimal Q-function), and the communication complexity (number of communication rounds). The table highlights the trade-off between sample and communication complexity, illustrating how algorithms with lower communication complexity might have higher sample complexity and vice versa. A lower bound on sample and communication complexity is also provided.

This table compares the sample and communication complexity of different single-agent and federated Q-learning algorithms. It shows the number of agents, sample complexity (number of samples needed to learn an epsilon-optimal Q-function), and communication complexity (number of communication rounds). Logarithmic factors and burn-in costs are omitted for simplicity. The table highlights that the proposed Fed-DVR-Q algorithm achieves order-optimal sample and communication complexities, outperforming existing algorithms.
Full paper#