↗ OpenReview ↗ NeurIPS Proc. ↗ Chat
TL;DR#
Reinforcement learning often faces the challenge of dealing with high-dimensional observations in real-world applications, while the underlying system dynamics might be relatively simple. Existing theoretical work frequently makes simplifying assumptions, like assuming small latent spaces or specific latent dynamic structures. This limits the applicability of these findings to more realistic scenarios.
This work develops a novel framework to analyze reinforcement learning under general latent dynamics. It introduces the concept of latent pushforward coverability as a key condition for statistical tractability. The researchers also present provably efficient algorithms that can transform any algorithm designed for the latent dynamics into one that works with rich observations. These algorithms are developed for two scenarios: one with hindsight knowledge of the latent dynamics, and one that relies on estimating latent models via self-prediction. The results offer a step toward a unified theory for RL under latent dynamics.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the critical challenge of reinforcement learning in complex environments with simpler underlying dynamics. It offers a unified statistical and algorithmic theory, moving beyond restrictive assumptions, and suggests new research directions in representation learning and RL algorithm design.
Visual Insights#
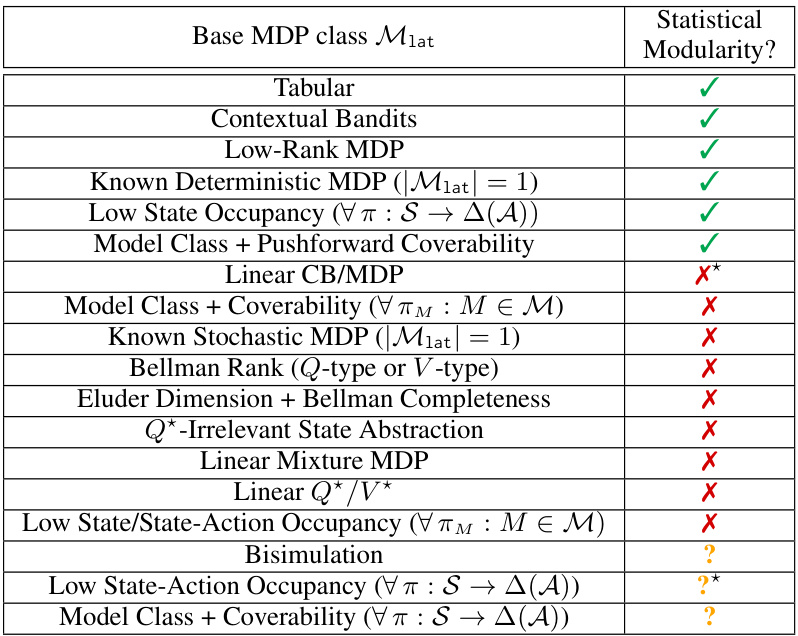
This table summarizes the statistical modularity results for various base MDP classes. It shows whether each class exhibits statistical modularity (meaning its sample complexity scales polynomially with the base class complexity and decoder class size) or not, using a specific complexity measure. It highlights that most well-studied function approximation settings lack statistical modularity when latent dynamics are introduced. It also points out cases where statistical modularity is achievable under specific conditions or assumptions (such as pushforward coverability). Open questions are identified for certain classes where it’s unclear whether statistical modularity is attainable.
Full paper#



















