Maximum Entropy Inverse Reinforcement Learning of Diffusion Models with Energy-Based Models

↗ OpenReview ↗ NeurIPS Proc. ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents a novel approach to improve the sample quality of diffusion models, particularly when the number of generation steps is small. This is a significant challenge in generative modeling, and the proposed method offers a potential solution that could have a broad impact on various applications. The introduction of maximum entropy IRL and dynamic programming provides new techniques for training diffusion models and EBMs, opening avenues for further research in both areas. The ability to train strong EBMs without relying on MCMC is another key contribution, addressing a long-standing limitation of energy-based models.

Visual Insights

#

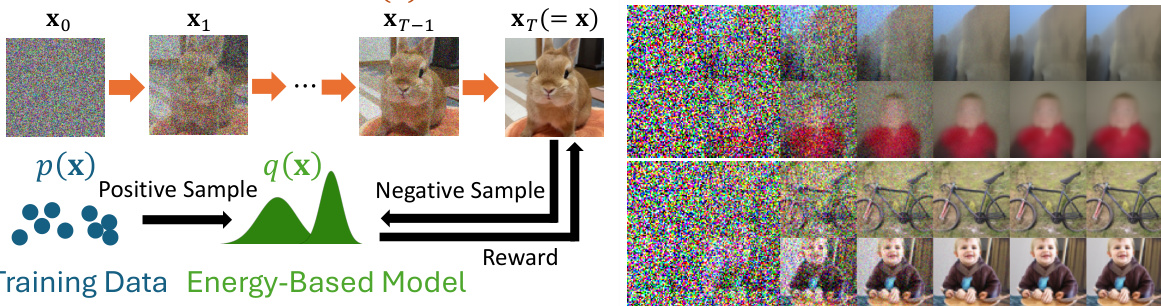
This figure illustrates the DxMI framework. The left panel shows a schematic diagram of how the diffusion model (π(x)) and the energy-based model (EBM, q(x)) interact during training. The diffusion model generates samples, and these samples are used to train the EBM, which in turn provides a reward signal for the diffusion model. This creates a feedback loop to refine the model. The right panel displays ImageNet 64 generation examples. The top row shows images generated by a 10-step diffusion model before fine-tuning with DxMI; the bottom row shows images generated after fine-tuning, highlighting the improvement in image quality achieved by DxMI.

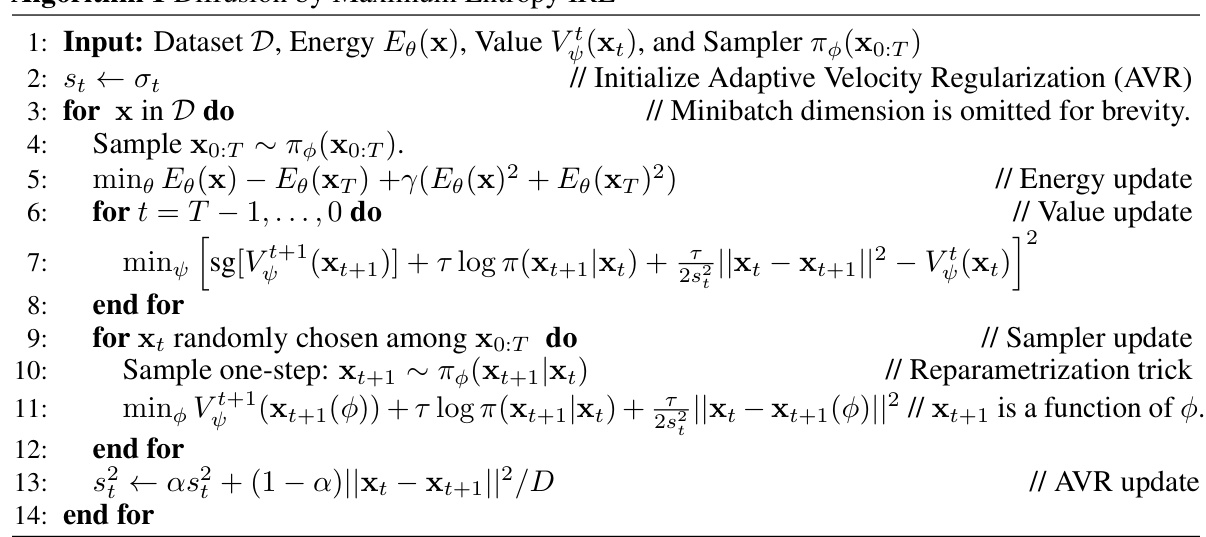
This table presents a quantitative comparison of different methods for density estimation on a synthetic dataset of 8 Gaussians. The methods compared include various diffusion models with different numbers of timesteps (T), with and without the DxMI fine-tuning. The performance is evaluated using two metrics: Sliced Wasserstein Distance (SW), measuring the distance between the generated samples and the true data distribution; and Area Under the Curve (AUC) of the energy-based model’s ability to discriminate between data samples and uniform noise. Lower SW indicates better sample quality, and higher AUC indicates better discriminative ability of the energy model. The table shows that DxMI consistently improves the sample quality and the discriminative power of the energy model, especially when the number of timesteps is small.

In-depth insights

#

MaxEnt IRL for Diffusion

#

The concept of ‘MaxEnt IRL for Diffusion’ blends maximum entropy inverse reinforcement learning (MaxEnt IRL) with diffusion models for generative modeling. MaxEnt IRL offers a principled way to learn reward functions from expert demonstrations, promoting exploration and diverse behavior. By applying MaxEnt IRL to diffusion models, we can potentially guide the diffusion process, enhancing sample quality and generation speed. This approach addresses challenges in traditional diffusion models, where slow generation and limitations in sample diversity are prevalent. The log probability density estimated from training data can be used as a reward, shaping the diffusion trajectory to better match the data distribution. The key advantage is its ability to accelerate sampling speed without relying on extensive pre-training, making it computationally efficient. However, challenges such as the computational cost of estimating log probability density, and the potential instability during training still need further investigation.

DxMI: A Minimax

#

The heading “DxMI: A Minimax” suggests a core methodology in the research paper that leverages a minimax framework for training diffusion models. DxMI, likely short for “Diffusion by Maximum Entropy Inverse Reinforcement Learning,” uses a minimax formulation to balance the goals of fitting the model to the data and maximizing the entropy of the generated samples. The minimax game involves two components: the diffusion model and an energy-based model (EBM). The EBM estimates the log probability density of the data, guiding the diffusion model’s training. Maximizing entropy is crucial as it promotes exploration, avoiding overfitting and enhancing sample diversity. This dual optimization is likely performed iteratively, where the diffusion model is updated to maximize its expected reward (log probability estimated by the EBM) and the EBM is updated to better fit the data distribution based on samples generated by the diffusion model, thus leading to a better representation of the underlying data distribution. The equilibrium of the minimax process represents the data density matched by the EBM and the diffusion model, ideally generating high-quality samples. The minimax framework thus combines the power of maximum entropy RL with the efficient sampling mechanism of diffusion models. This approach is especially beneficial for limited generation steps, where the approach addresses the typical sample quality degradation encountered in such settings.

DxDP: Dynamic Prog

#

The heading ‘DxDP: Dynamic Prog’ likely introduces a novel algorithm, DxDP, employing dynamic programming principles. This suggests a departure from traditional backpropagation methods common in diffusion model training. DxDP likely offers computational advantages by breaking the optimization problem into smaller, manageable subproblems across time steps. The use of dynamic programming is especially beneficial for overcoming the challenges of gradient instability and computational costs associated with long diffusion trajectories, enabling efficient updates to the diffusion model’s parameters. The algorithm likely leverages value functions, crucial for dynamic programming, to guide the optimization process. This approach might result in faster convergence and improved sample quality, especially when dealing with limited generation time steps. The effectiveness of DxDP in training diffusion models with few steps is a key focus, and its performance relative to traditional methods is likely a central evaluation point. Its potential broader application beyond the specific context of DxMI (Maximum Entropy IRL), for instance, in fine-tuning diffusion models with human feedback, hints at a significant contribution to the field.

Short-Run Diffusion

#

The concept of “Short-Run Diffusion” in generative modeling addresses the inherent limitation of diffusion models, which typically require numerous time steps for high-quality sample generation. Faster generation is crucial for practical applications; however, reducing the number of steps often leads to a degradation in sample quality. This challenge arises from the distribution shift between training (often using many steps) and generation (using fewer steps). Methods for addressing short-run diffusion involve techniques that either modify the sampling process of the pre-trained diffusion model or fine-tune the model itself for faster convergence. Fine-tuning methods such as those employing inverse reinforcement learning or adversarial training aim to guide the model towards better sample quality in fewer steps, often by leveraging reward functions derived from the data distribution or through adversarial training with discriminators. These techniques aim to balance speed and quality, but finding the optimal trade-off remains an area of active research. The success of short-run diffusion ultimately depends on designing effective algorithms that address the distribution shift while maintaining the model’s generative capabilities. Maximum entropy approaches that encourage exploration and model stability are promising avenues.

EBM Training w/o MCMC

#

Training Energy-Based Models (EBMs) typically relies on computationally expensive Markov Chain Monte Carlo (MCMC) methods. This paper introduces a novel approach that eliminates the need for MCMC, leveraging a diffusion model to train the EBM effectively. The method frames EBM training as a minimax problem, where the diffusion model and EBM are jointly optimized. The diffusion model is trained using the log probability density estimated by the EBM as a reward, while the EBM itself is optimized to fit the data distribution represented by the diffusion model’s samples. This method leads to improved efficiency and stability in EBM training, as demonstrated in the experimental results. By sidestepping MCMC, the method facilitates broader applicability of EBMs, particularly in resource-constrained settings or tasks requiring faster training times. The absence of MCMC also enhances the control and interpretability of the EBM training process, reducing sensitivity to hyperparameter choices inherent in MCMC approaches. The results demonstrate a considerable performance gain, enabling high-quality sample generation and anomaly detection.

More visual insights

#

More on figures

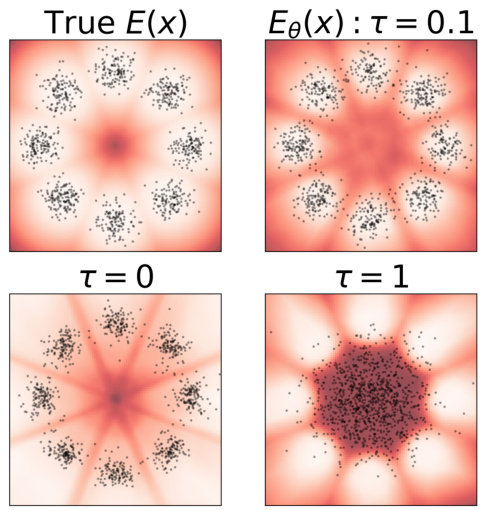
This figure visualizes the results of a 2D density estimation experiment using 8 Gaussian distributions. The left two panels show the true energy function (E(x)) for the data, with white representing low energy and dark red representing high energy. The dots represent the generated samples from the model at different temperature settings (τ=0 and τ=1). The right two panels illustrate the estimated energy function (Eθ(x)) learned by the DxMI model at the same temperature settings (τ=0 and τ=1), also with white indicating low energy and dark red representing high energy. By comparing the left and right panels, one can assess the accuracy of the DxMI model in estimating the true energy function, and the impact of temperature (τ) on the quality of density estimation, with the samples providing a visualization of the energy function’s effect on sample distribution.

This figure visualizes the learned value functions V(x, t) at different time steps (t=0 to t=5) during the training process of the Diffusion by Maximum Entropy Inverse Reinforcement Learning (DxMI) model. Each image represents a 2D heatmap where color intensity corresponds to the value function’s output for a given input x. Darker blue indicates lower values, and lighter blue indicates higher values. The final time step (t=5) represents the energy function E(x) learned by the energy-based model (EBM). The figure shows how the value function changes over time as it learns to approximate the data distribution.

This figure compares image samples generated by three different methods: real CIFAR-10 images, samples generated using SFT-PG (a baseline method), and samples generated using DxMI (the proposed method). Both SFT-PG and DxMI used 10 generation steps (T=10). The FID (Fréchet Inception Distance) scores are provided to quantify the quality of the generated images, with lower scores indicating better quality. DxMI achieves a lower FID score (3.19) compared to SFT-PG (4.32), suggesting that DxMI produces higher-quality samples.

This figure compares image samples generated by different models: the original ImageNet data, a Consistency Model (a baseline model for generating images using a diffusion process in one step), and the proposed DxMI model trained with 4 and 10 steps. The visual comparison highlights that DxMI produces higher-quality images, particularly when it comes to accurately representing human faces, which are often distorted by the baseline model.

More on tables

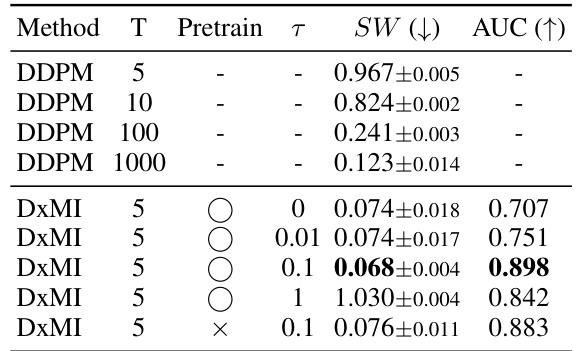
This table presents quantitative results of a 2D density estimation experiment using 8 Gaussian distributions. It compares different methods (DDPM and DxMI with varying hyperparameters) by measuring the sliced Wasserstein distance (SW) between generated samples and the ground truth data, and the Area Under the Curve (AUC) of the energy-based model’s ability to discriminate between data and uniform noise. Lower SW indicates better sample quality, while higher AUC indicates better anomaly detection performance. The standard deviation is reported for 5 independent runs, and the ideal maximum AUC is given for reference.

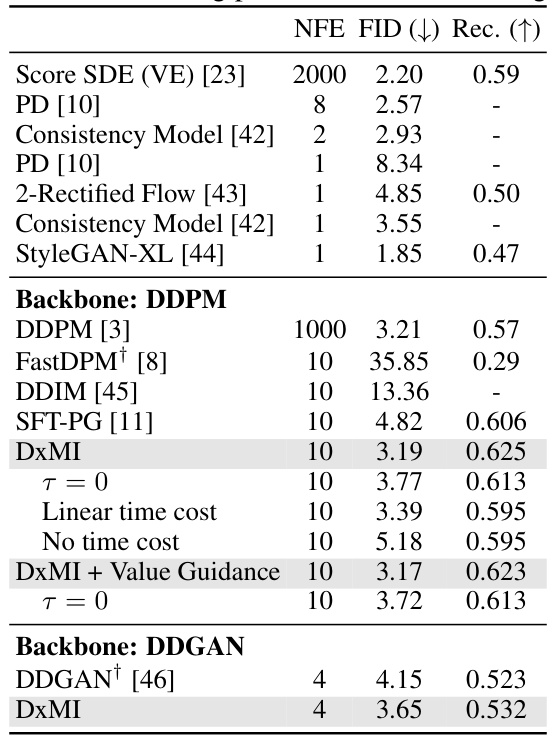
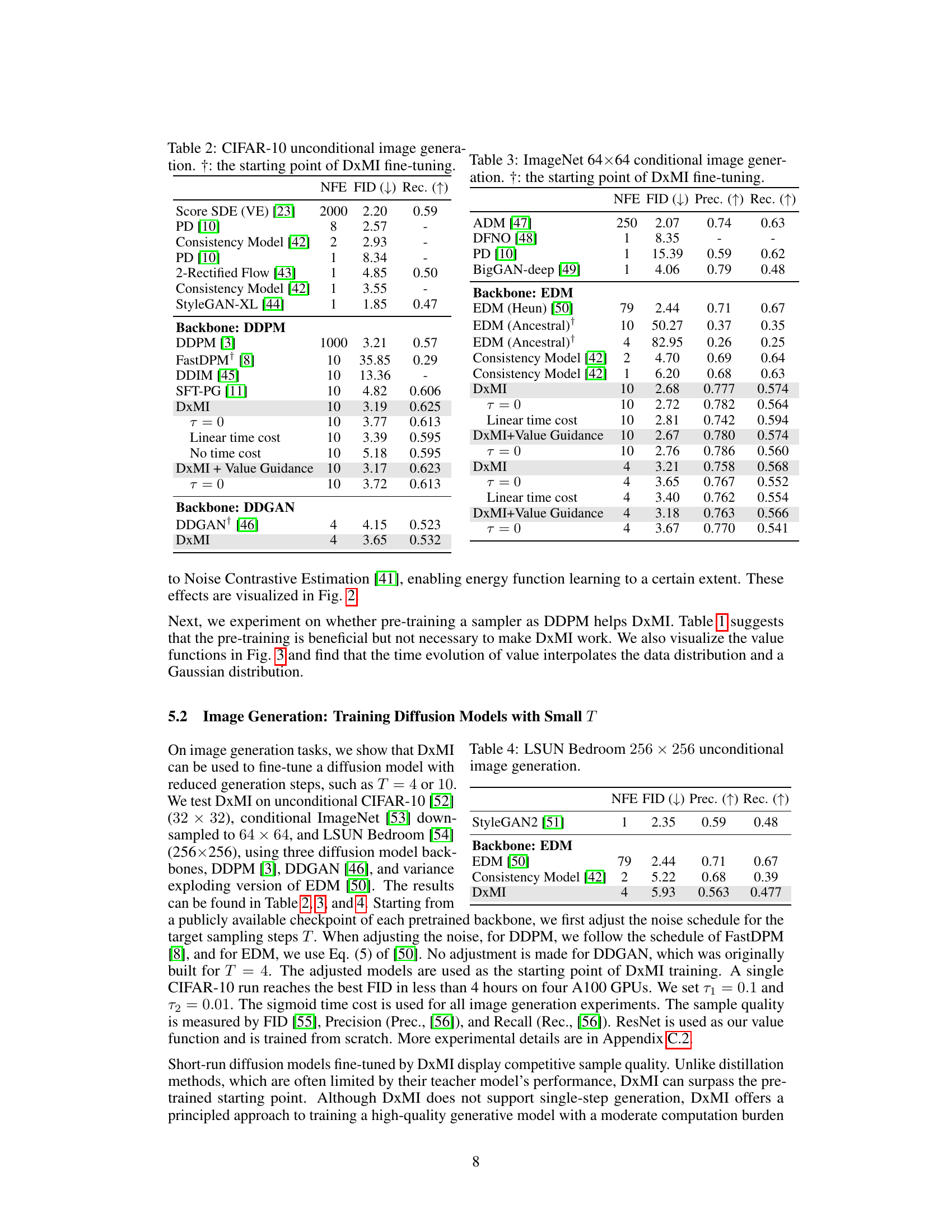
This table presents the quantitative results of unconditional image generation on the CIFAR-10 dataset. It compares several different methods, including Score SDE, PD, Consistency Models, and StyleGAN-XL, to the proposed DxMI method and its variants (with different time cost functions, etc.). The results are reported using FID (Fréchet Inception Distance) and Recall, lower FID and higher Recall indicating better sample quality. The ‘†’ symbol indicates the starting point for fine-tuning using DxMI.

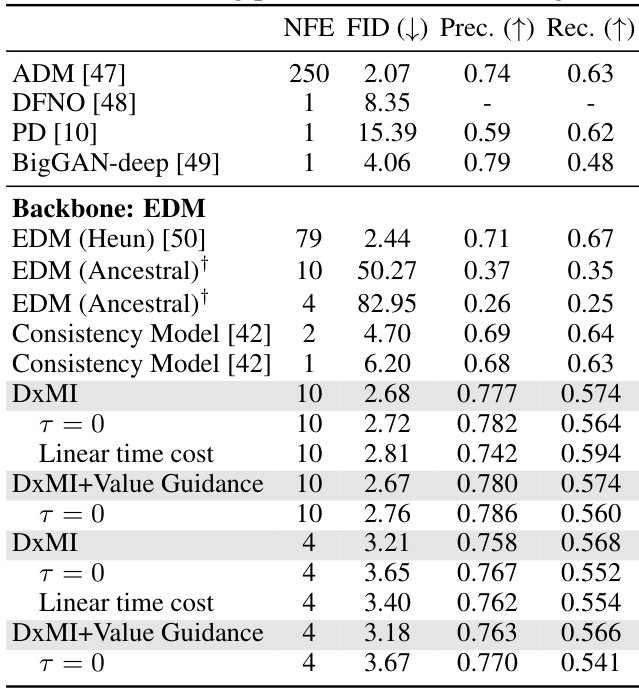
This table presents the results of applying different methods for conditional image generation on the ImageNet 64x64 dataset. It compares the performance of several approaches, including different diffusion models and the proposed DxMI method, in terms of FID (Fréchet Inception Distance), Precision, and Recall. The number of forward passes (NFE) required for generation is also shown. The † symbol indicates the starting point from which DxMI fine-tuning begins.

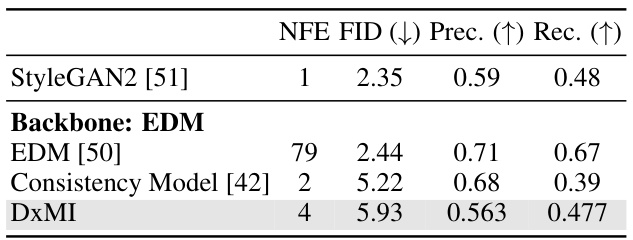
This table presents the results of unconditional image generation on the LSUN Bedroom dataset (256x256 resolution). It compares the performance of several models, including StyleGAN2, EDM, Consistency Model, and DxMI, in terms of FID (Fréchet Inception Distance), Precision, and Recall. The number of function evaluations (NFE) required for generation is also shown. Lower FID indicates better image quality, while higher precision and recall indicate that generated images better match the true distribution of the data.

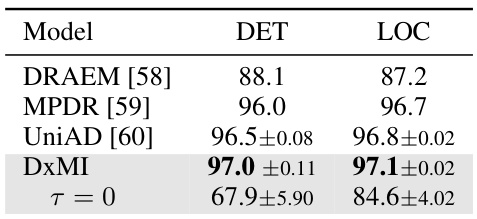
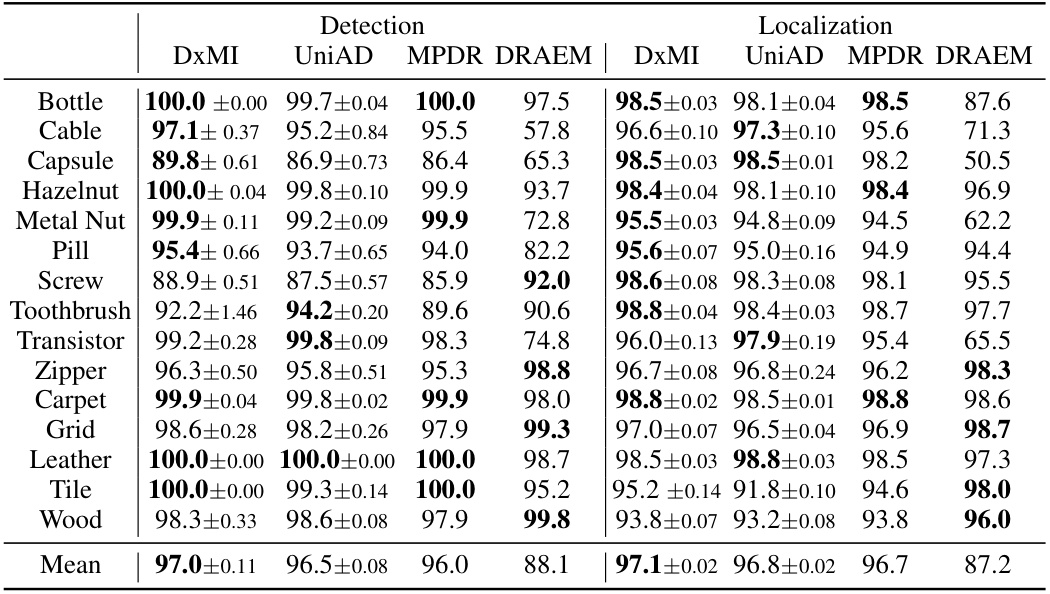
This table shows the performance of DxMI and other methods on the MVTec-AD anomaly detection dataset. The AUC scores for both anomaly detection and localization are reported. DxMI achieves the highest AUC for both tasks, highlighting its effectiveness in this application. The results for τ=0 show the importance of entropy maximization in DxMI.

This table presents a quantitative comparison of different methods for density estimation on a synthetic dataset of 8 Gaussian distributions. The methods are compared using two metrics: the sliced Wasserstein distance (SW), measuring the distance between the generated samples and the true data distribution, and the Area Under the Curve (AUC) of a classifier trained to distinguish between generated samples and uniform noise. Lower SW values and higher AUC values indicate better performance. The table also shows the number of function evaluations (T) used in each method.

Full paper

#