Achieving Constant Regret in Linear Markov Decision Processes

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it offers the first algorithm achieving a constant regret bound in reinforcement learning with linear function approximation, even when the model is misspecified. This addresses a major limitation of existing RL algorithms and opens doors for more robust and efficient RL applications in various real-world scenarios. It also provides valuable insights into theoretical guarantees in RL.

Visual Insights

#

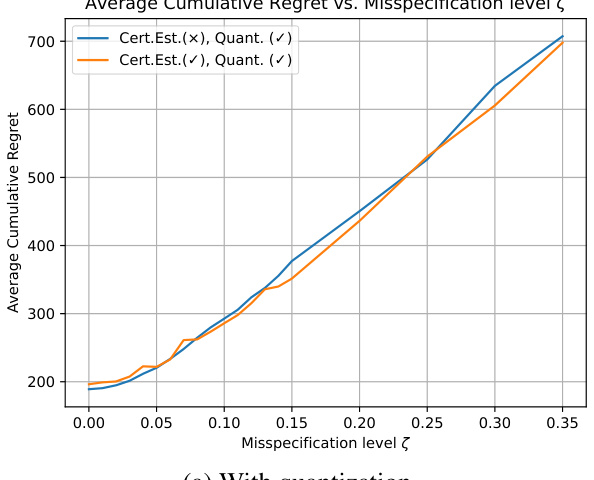
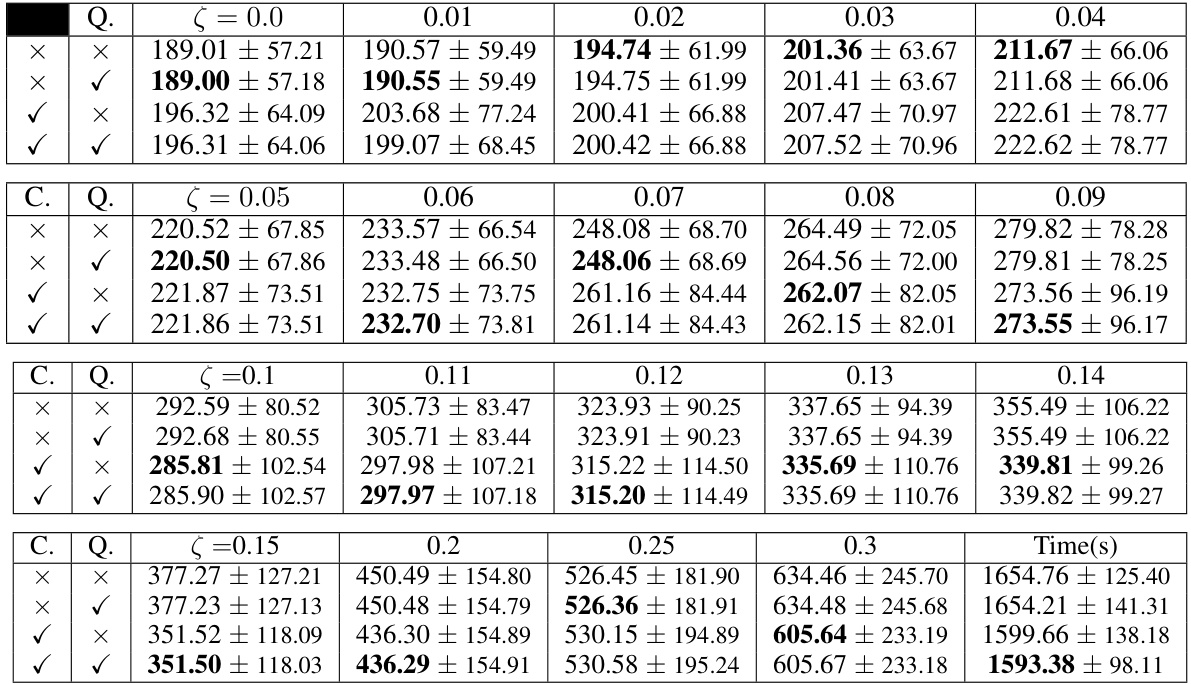
🔼 This figure shows the relationship between the average cumulative regret and the misspecification level (ζ) over 2000 episodes. The experiment was repeated 16 times with different random seeds to get an average performance and reduce the impact of randomness on the results. The x-axis represents the misspecification level (ζ), and the y-axis represents the average cumulative regret. Two lines are plotted in each subplot, one is the algorithm with the certified estimator and quantization, and the other is without the certified estimator. The plot shows how the cumulative regret increases with the misspecification level.

read the caption

Figure 1: Cumulative regret over 2000 episodes with respect to different misspecification level ζ. The result is averaged over 16 individual environments.

🔼 This table compares three different reinforcement learning algorithms under the linear Markov Decision Process (MDP) setting. It shows the instance-dependent regret bounds achieved by each algorithm, highlighting the dependence on factors like the feature dimension (d), horizon (H), and suboptimality gap (Δ). It also notes whether the algorithm can handle misspecified MDPs, where the transition kernel and reward function may not perfectly match linear approximations.

read the caption

Table 1: Instance-dependent regret bounds for different algorithms under the linear MDP setting. Here d is the dimension of the linear function (s, α), H is the horizon length, Δ is the minimal suboptimality gap. All results in the table represent high probability regret bounds. The regret bound depends the number of episodes K in He et al. (2021a) and the minimum positive eigenvalue λ of features mapping in Papini et al. (2021b). Misspecified MDP? indicates if the algorithm can (✓) handle the misspecified linear MDP or not (×).

In-depth insights

#

Cert-LSVI-UCB Algo

#

The proposed Cert-LSVI-UCB algorithm represents a novel approach to achieving constant regret in reinforcement learning, particularly within the context of linear Markov Decision Processes (MDPs). Its core innovation lies in a novel certified estimator. This estimator enables a more precise analysis of the multi-phase value-targeted regression, allowing for a high-probability regret bound that is independent of the number of episodes. The algorithm cleverly handles model misspecification, a key challenge in real-world RL applications, without relying on strong assumptions about data distribution. By incorporating this certified estimator, Cert-LSVI-UCB demonstrates the potential to overcome limitations of prior work which exhibited logarithmic regret growth with the number of episodes. The instance-dependent regret bound achieved showcases the algorithm’s efficacy in tackling various problem instances, a significant improvement over existing, worst-case analysis methods.

Constant Regret

#

The concept of “constant regret” in reinforcement learning signifies an algorithm achieving a finite regret even over an infinite number of episodes. This is a significant improvement over traditional regret bounds that scale with the square root or logarithm of the number of episodes. Constant regret implies that the algorithm learns the optimal policy within a fixed number of mistakes, regardless of the duration of interaction with the environment. The research focuses on achieving this desirable property under the setting of linear Markov decision processes (MDPs), where both the transition dynamics and reward functions are linear combinations of feature vectors. A key challenge addressed involves handling model misspecification, where the assumed linear models might imperfectly represent the true dynamics. The authors propose a novel algorithm, Cert-LSVI-UCB, that leverages a certified estimator to achieve a high-probability constant regret bound, demonstrating its effectiveness without strong assumptions about data distributions. The instance-dependent regret bound highlights that the algorithm’s performance is tied to problem-specific characteristics, such as the minimum suboptimality gap. This work represents a step towards bridging the gap between theoretical guarantees and practical expectations in reinforcement learning, providing strong theoretical foundations for algorithms that learn quickly and efficiently.

Misspec Linear MDP

#

The concept of a misspecified linear Markov Decision Process (MDP) is crucial for bridging the gap between theoretical reinforcement learning (RL) and practical applications. Linear MDPs offer a structured approach to RL, simplifying analysis and enabling efficient algorithms. However, real-world problems rarely conform perfectly to the linear assumption. Misspecification acknowledges this reality, introducing error into the transition dynamics and reward model. Analyzing RL in this context is important because it reflects the challenges of applying theoretical algorithms to real-world scenarios. The degree of misspecification directly impacts the regret bounds achieved by algorithms; thus robust algorithms need to be designed that account for and adapt to this inherent model uncertainty. The research on misspecified linear MDPs, therefore, focuses on developing theoretically sound algorithms with performance guarantees despite the model inaccuracies. Instance-dependent bounds become particularly relevant, offering a more nuanced understanding of algorithm performance depending on the specific MDP characteristics. Ultimately, research in this area advances the field by providing more realistic and applicable RL solutions that are less sensitive to modeling imperfections.

Future Research

#

Future research directions stemming from this paper on achieving constant regret in reinforcement learning could explore relaxing the strong assumptions made, such as the linear function approximation and the specific misspecification model. Investigating alternative function approximation methods or dealing with more general forms of misspecification would significantly broaden the applicability of the findings. Another critical avenue would be to improve the sample complexity of the proposed algorithm and analyze the trade-offs between computational cost and regret guarantees. Addressing the limitations of current theoretical analyses and pushing the boundaries of achieving high-probability constant regret bounds under less restrictive assumptions would also be significant. Finally, empirical evaluations on real-world tasks are crucial to validating the theoretical claims and assessing the practical performance of this approach. This would involve carefully choosing benchmark tasks that challenge the assumptions to fully evaluate the robustness of the methods.

Limitations

#

The research paper’s limitations section would ideally address several key aspects. Firstly, it should acknowledge any assumptions made during the theoretical analysis, such as those about the data distribution or the linear nature of the model. These assumptions often simplify the analysis but may not always hold in real-world settings. Secondly, the algorithm’s dependence on key parameters, like the dimensionality of the feature space or the planning horizon, should be critically examined. The paper should discuss whether the algorithm’s performance scales efficiently with these factors. It’s also crucial to discuss any limitations with respect to the misspecification level. The paper should explore the range of misspecification for which the constant regret guarantee holds, and how performance degrades when this level is exceeded. Finally, a discussion of practical considerations such as computational cost and the need for parameter tuning would be valuable to improve the understanding and applicability of the proposed approach.

More visual insights

#

More on figures

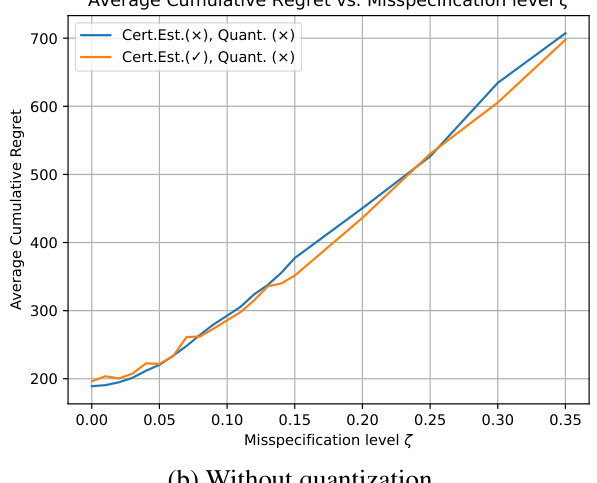
🔼 This figure shows the relationship between the average cumulative regret and the misspecification level (ζ) of the linear Markov Decision Process (MDP). Two lines represent the average cumulative regret with and without quantization. The x-axis represents the misspecification level ζ, and the y-axis represents the average cumulative regret. The figure shows that as the misspecification level increases, the average cumulative regret also increases. It also shows that the quantization has minimal effect on the regret.

read the caption

Figure 1: Cumulative regret over 2000 episodes with respect to different misspecification level ζ. The result is averaged over 16 individual environments.

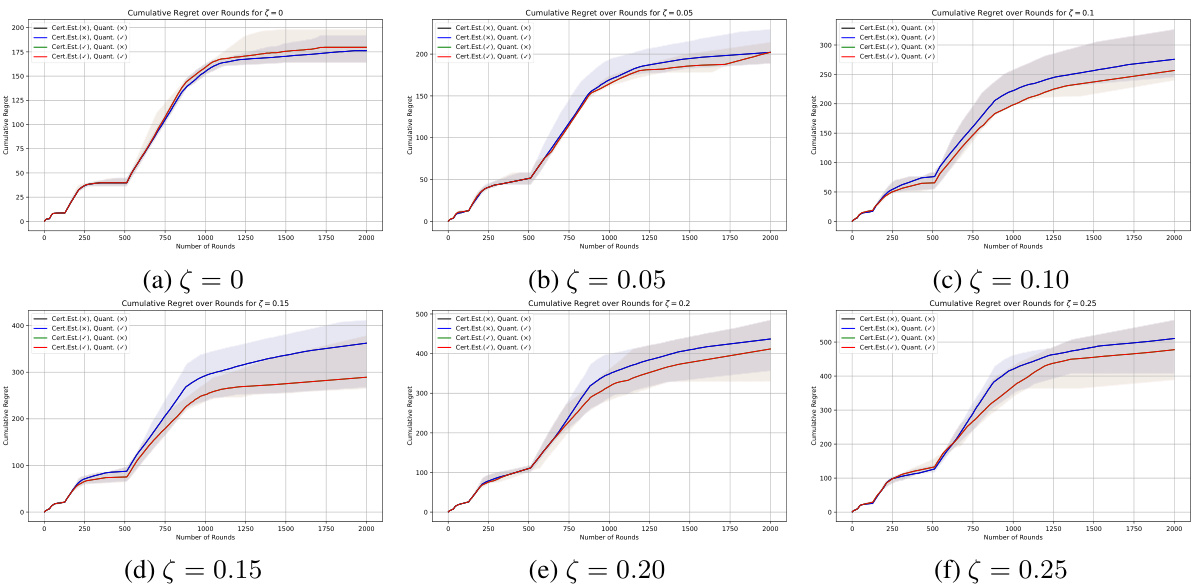
🔼 This figure displays the cumulative regret for six different misspecification levels (ζ = 0, 0.05, 0.1, 0.15, 0.2, 0.25). Each level has three lines: one using the proposed Cert-LSVI-UCB algorithm with both certified estimation and quantization; another using Cert-LSVI-UCB without quantization; and a third using the Cert-LSVI-UCB without certified estimation. The shaded area represents the 25th to 75th percentile range across 16 different environments, giving a sense of the variability in the results.

read the caption

Figure 2: Cumulative regret with respect to the number of episodes. We reported the median cumulative regret with the shadow area as the region from 25% percentage to 75% percentage statistics over 16 runs.

More on tables

🔼 This table compares the instance-dependent regret bounds achieved by different reinforcement learning algorithms for linear Markov Decision Processes (MDPs). It contrasts algorithms that can handle misspecified MDPs (where the reward and transition functions are only approximately linear) with those that cannot. The table shows that the proposed algorithm, Cert-LSVI-UCB, achieves a constant regret bound with high probability, unlike other methods which exhibit logarithmic or square-root dependence on the number of episodes.

read the caption

Table 1: Instance-dependent regret bounds for different algorithms under the linear MDP setting. Here d is the dimension of the linear function (s, α), H is the horizon length, ∆ is the minimal suboptimality gap. All results in the table represent high probability regret bounds. The regret bound depends the number of episodes K in He et al. (2021a) and the minimum positive eigenvalue λ of features mapping in Papini et al. (2021b). Misspecified MDP? indicates if the algorithm can (✓) handle the misspecified linear MDP or not (×).

🔼 The table compares instance-dependent regret bounds of three different algorithms for linear Markov Decision Processes. It shows how the regret scales with problem parameters (dimension of feature space, horizon length, suboptimality gap) and whether the algorithm can handle model misspecification. Key differences between the algorithms are highlighted.

read the caption

Table 1: Instance-dependent regret bounds for different algorithms under the linear MDP setting. Here d is the dimension of the linear function (s, α), H is the horizon length, ∆ is the minimal suboptimality gap. All results in the table represent high probability regret bounds. The regret bound depends the number of episodes K in He et al. (2021a) and the minimum positive eigenvalue λ of features mapping in Papini et al. (2021b). Misspecified MDP? indicates if the algorithm can (✓) handle the misspecified linear MDP or not (×).

Full paper

#