TL;DR#
Many machine learning algorithms use stochastic methods, but understanding how well these algorithms generalize to unseen data remains a challenge. A key problem is bounding the generalization gap, or the difference between an algorithm’s performance on training data versus new data. This paper tackles this challenge by focusing on a class of stochastic algorithms that produce probability distributions according to a Hamiltonian function. Existing bounds often come with unnecessary limitations or include extra terms that are difficult to interpret.
This work introduces a novel, more efficient method for bounding the generalization gap of algorithms with Hamiltonian dynamics. The core idea involves bounding the log-moment generating function, which quantifies the algorithm’s output distribution’s concentration around its mean. The paper offers new theoretical guarantees for Gibbs sampling, randomized stable algorithms, and extends to sub-Gaussian hypotheses. These improved bounds are simpler and remove superfluous logarithmic factors and terms, significantly advancing the field.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in machine learning and statistics because it offers novel generalization bounds for stochastic learning algorithms, particularly those based on Hamiltonian dynamics. These bounds are tighter and more broadly applicable than existing ones, improving our understanding of algorithm performance and enabling the development of more effective methods. The work also opens avenues for future research in PAC-Bayesian bounds with data-dependent priors and the analysis of uniformly stable algorithms. It is relevant to current trends in deep learning and stochastic optimization where generalization is a key challenge.
Visual Insights#
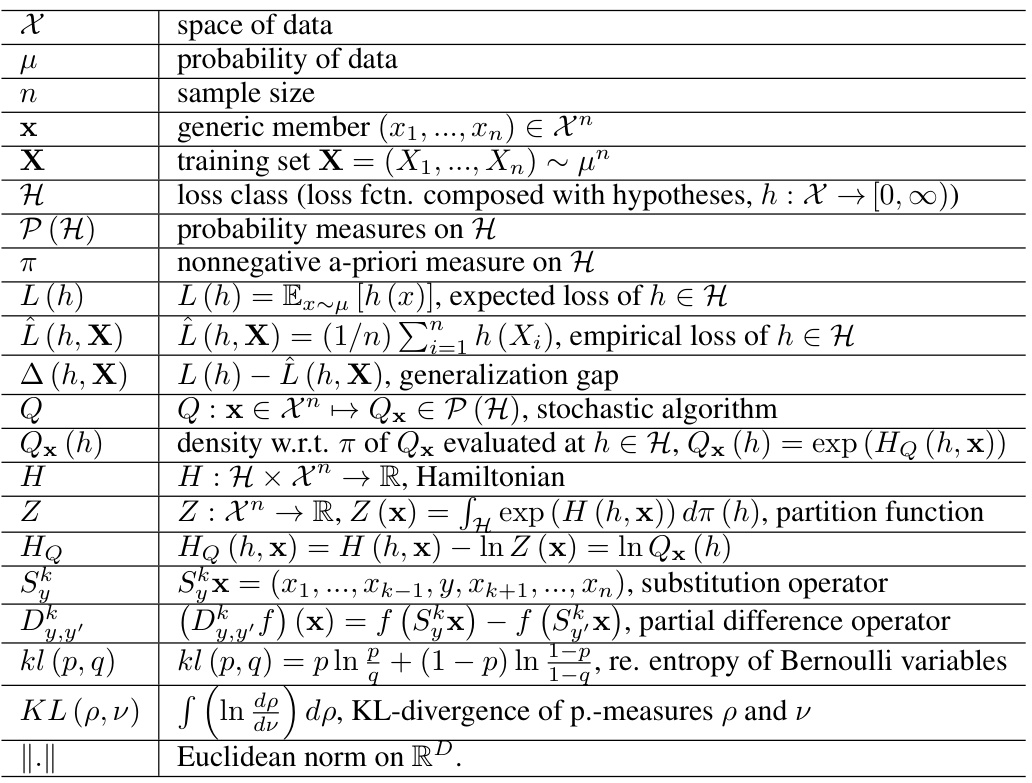
🔼 This table lists the notations used throughout the paper. It includes notations for mathematical objects such as spaces, measures, functions, algorithms, and their properties. The table serves as a quick reference for the symbols and their meanings, making it easier to follow the mathematical derivations and arguments.
read the caption
C Table of notation
Full paper#



















