TL;DR#
Classical algorithms for market equilibrium computation, although efficient for smaller markets, struggle with the scalability demands of modern internet-based applications like auctions and recommender systems. The main challenge lies in the computational cost of these algorithms which grows proportionally with the number of buyers and goods. This necessitates the need for more efficient algorithms that can solve the market equilibrium problem faster, especially in the large-scale settings prevalent in today’s applications.
This research introduces a novel quantum algorithm that significantly improves the computational efficiency of market equilibrium computations. By leveraging the power of quantum computing, this algorithm achieves sublinear performance, outperforming existing classical algorithms. This translates to a significant speedup, especially when dealing with many buyers and goods. The theoretical findings are also supported by experimental results, demonstrating the practical efficacy of the quantum algorithm.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in market equilibrium computation and quantum computing. It bridges the gap between theoretical economics and quantum algorithms, offering a new avenue for tackling large-scale problems. The sublinear quantum algorithm presented could significantly impact various applications dealing with large datasets and complex optimization tasks, such as auctions and recommender systems. Furthermore, the work inspires further research on the integration of quantum algorithms into other economic models and beyond.
Visual Insights#
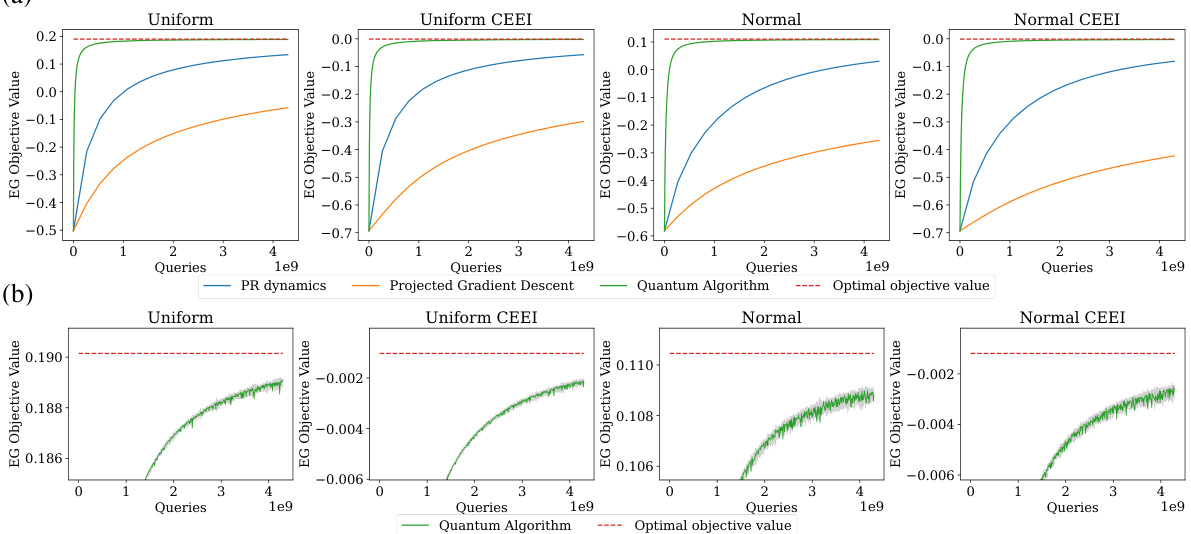
🔼 This figure presents the results of numerical simulations comparing the performance of three algorithms for computing market equilibrium: the Proportional Response (PR) dynamics, projected gradient descent, and the proposed quantum algorithm. The top row (1a) shows the convergence of the EG objective function for four different scenarios (uniform, uniform CEEI, normal, normal CEEI) against the number of queries. The bottom row (1b) displays the convergence behavior of the quantum algorithm, highlighting its faster convergence in the mid-accuracy regime. It illustrates how the quantum algorithm outperforms both PR dynamics and projected gradient descent, supporting the paper’s theoretical findings.
read the caption
Figure 1: Experimental results. We perform our experiments on n = 16384 buyers and goods given the same amount of queries for all algorithms. We observe in Figure 1a that over different distributions, our quantum algorithm (green) significantly outperforms the PR dynamics (blue), which aligns with our theoretical results. Furthermore, our results also show that both our quantum algorithm and the PR dynamics outperform projected gradient descent (orange) in the mid-accuracy regime. Figure 1b shows the convergence of a single run of the quantum algorithm despite its instability from faulty updates, as well as the variance over the multiple runs (shaded in grey).

🔼 This table summarizes the main results of the paper by comparing the performance of the classical proportional response (PR) dynamics algorithm and the proposed quantum algorithm for market equilibrium computation. It shows the number of iterations, runtime, memory usage, and the time required to prepare the results for both algorithms. The comparison highlights the quantum algorithm’s polynomial speedup in terms of runtime and memory.
read the caption
Table 1: Main results. In this work, n is the number of buyers, m is the number of goods, and ε indicates the additive error of the computed values to the minimally-achievable EG objective value. The memory complexity for the quantum algorithm (annotated with *) refers to the use of quantum query access to classical memory, achievable by QRAM (see Definition 3), instead of classical RAM. As the computed competitive equilibrium consumes O(mn) memory, our quantum algorithm does not provide the entire bid matrix, but instead provides quantum query access (QA) and sample access (SA) to the competitive equilibrium. The result preparation column refers to the additional runtime cost of preparing QA and SA.
Full paper#



















