TL;DR#
Current neural implicit shape representations often lack detail or are computationally expensive due to their reliance on large numbers of parameters. They often use a single latent code for an entire shape, making representation of complex geometries difficult and inefficient. Local surface-based methods offer improvement but increase parameters. This limits their applications.
CoFie addresses these limitations by introducing Coordinate Fields, which compress the spatial complexity of local shapes. This innovative method makes the MLP-based implicit surface representation much more efficient and accurate. CoFie also uses quadratic layers to improve geometry modeling, thereby increasing expressiveness. The results demonstrate significant improvements in accuracy and efficiency compared to existing methods, achieving comparable performance with 70% fewer parameters.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel, efficient neural surface representation (CoFie) that significantly improves shape representation accuracy and reduces computational costs. This addresses a major challenge in 3D shape modeling and opens new avenues for research in efficient and accurate implicit surface representations. Its generalizability and performance gains are highly relevant to various applications involving 3D shape processing.
Visual Insights#

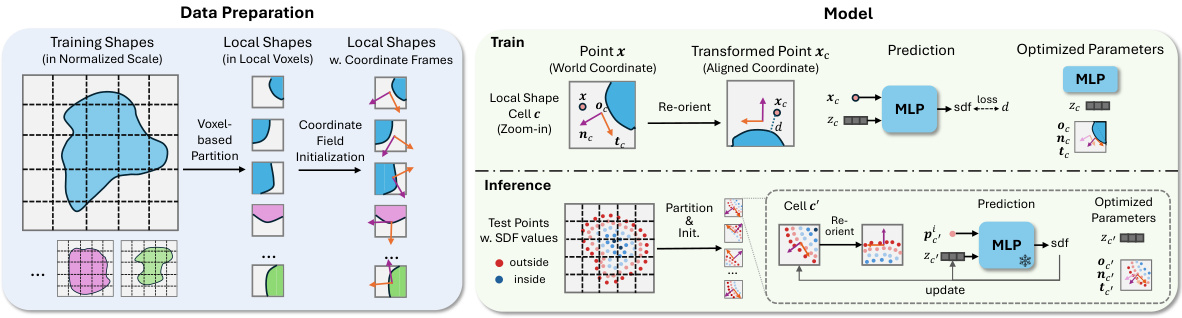
🔼 CoFie, a novel local geometry-aware neural surface representation, divides a shape into local patches. Each patch uses an MLP-based Signed Distance Function (SDF) for representation. The key innovation is the Coordinate Field, which assigns a learnable coordinate frame to each patch. This transforms the patches from the world coordinate system into an aligned system, significantly reducing their spatial complexity and making them easier to represent with the MLPs.
read the caption
Figure 1: CoFie is a local geometry-aware shape representation. (Left) CoFie divides a shape into non-overlapping local patches, where each local patch is represented by an MLP-based Signed Distance Function. (Right) CoFie introduces Coordinate Field, which attaches a coordinate frame to each local patch. It transforms local patches from the world coordinate system to an aligned coordinate system, reducing shape complexity.
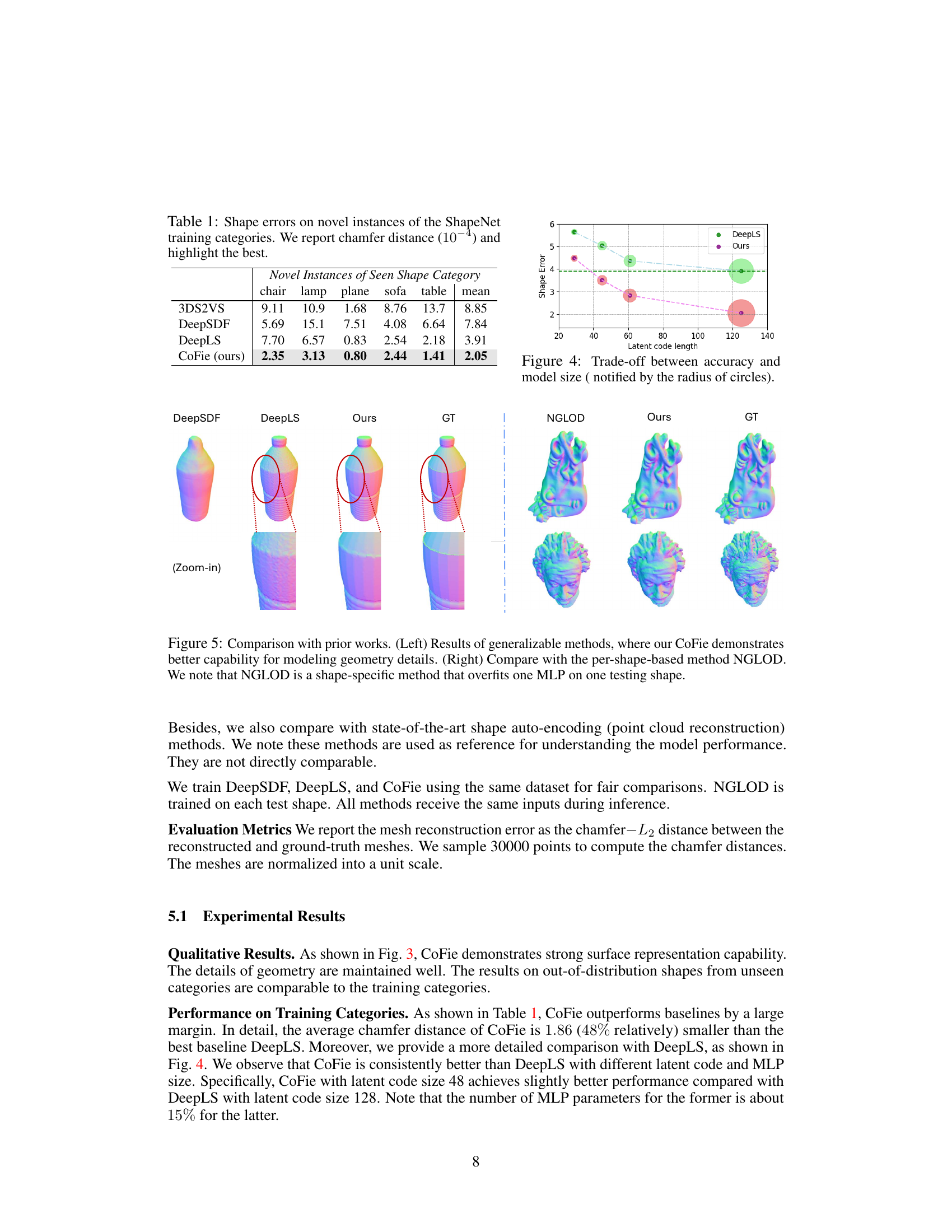
🔼 This table presents the quantitative results of the proposed CoFie method and compares it with other baseline methods. It shows the chamfer distance (a common metric for evaluating the accuracy of 3D shape reconstruction), which measures the average distance between the predicted shape and the ground truth shape. The results are reported for novel instances from the ShapeNet training categories, demonstrating how well the methods generalize to unseen data within the same categories. The best results for each category are highlighted, providing a direct comparison of CoFie’s performance against the baseline methods.
read the caption
Table 1: Shape errors on novel instances of the ShapeNet training categories. We report chamfer distance (10-4) and highlight the best.
In-depth insights#
Local SDF Analysis#
A hypothetical ‘Local SDF Analysis’ section in a research paper would delve into the mathematical properties of Signed Distance Functions (SDFs) when applied to localized regions of a 3D shape. It would likely explore how well quadratic functions approximate local surface geometry, a key assumption for many implicit surface representation methods. The analysis may involve deriving the SDF of a quadratic patch and exploring its sensitivity to transformations (rotation, translation). This is crucial because accurate SDF reconstruction relies on the ability to disentangle geometric information from the transformation parameters, a point often highlighted in such papers. Furthermore, the analysis might investigate the impact of different coordinate systems on the complexity and efficiency of fitting local SDFs. A well-aligned coordinate frame (e.g., defined by the normal and principal directions) is expected to simplify the representation, leading to better learning and compression of local shape data. The section could conclude by stating the implications of these findings for the design of efficient and accurate neural implicit shape representations, potentially justifying the use of techniques such as coordinate fields to simplify optimization and improve performance.
CoFie Architecture#
CoFie’s architecture is a hierarchical hybrid model, cleverly combining voxel-based coarse representation with local, fine-grained implicit neural surface representations. This design tackles the challenge of representing complex shapes efficiently. The voxel grid partitions the shape into manageable chunks, each containing a local patch. Each local patch is represented by an MLP-based SDF, but CoFie’s innovation lies in the incorporation of a learnable Coordinate Field. This field transforms each local patch into an aligned coordinate frame, simplifying the geometry and improving the MLP’s learning efficiency. Quadratic layers within the MLP further enhance the model’s expressiveness for local shape details. The system is trained end-to-end to optimize the coordinate fields and MLP parameters. The shared MLP applied across multiple voxel grids promotes generalization to unseen shapes, unlike previous methods that employed separate MLPs. This architecture balances accuracy and efficiency, enabling CoFie to outperform prior work.
Quadratic MLPs#
The use of Quadratic MLPs in neural implicit surface representations presents a compelling advancement in the field. Standard MLPs with ReLU activations are inherently piecewise linear, limiting their ability to accurately capture the non-linear nature of Signed Distance Functions (SDFs) that define complex 3D shapes. Quadratic MLPs offer a powerful solution to this by introducing quadratic layers into the network architecture. This modification allows for more expressive function approximations, enabling the model to learn the curved surfaces and subtle geometric details often missed by linear models. The introduction of quadratic terms significantly enhances the expressiveness of the network, particularly crucial when modeling local surface patches which may deviate substantially from linearity. However, this increase in expressiveness comes at a cost: quadratic layers introduce a significantly larger number of parameters compared to linear layers, posing challenges for training efficiency and the risk of overfitting. The choice of incorporating quadratic layers must therefore involve careful consideration of model complexity and training data availability. Further research could investigate optimal strategies for managing the complexity of quadratic MLPs, potentially through the use of regularization techniques or architectural innovations, to harness their considerable potential for representing intricate surface geometries while maintaining reasonable computational costs.
Generalization Ability#
The paper’s core contribution lies in enhancing the generalization ability of neural implicit surface representations. This is achieved through a novel local geometry-aware approach, CoFie, which cleverly separates the transformation information of local surface patches from their inherent geometric details. By introducing a learnable “Coordinate Field,” CoFie aligns local patches, significantly reducing their spatial complexity and simplifying the learning task for MLP-based implicit functions. This design is theoretically grounded in an analysis of local SDFs and their quadratic approximation, showing that local shapes are highly compressible in an aligned coordinate frame. The incorporation of quadratic layers within the MLP further improves the model’s capacity to capture fine-grained geometric details. Experiments demonstrate that CoFie substantially outperforms existing methods, exhibiting a significant reduction in shape error, particularly on unseen shape categories, highlighting its strong generalization capabilities. CoFie’s effectiveness is validated through comparisons with both generalizable and shape-specific baselines, confirming its ability to achieve comparable performance even with fewer parameters. The results underscore CoFie’s ability to generalize to unseen shapes and real-world data, proving it a significant advancement in robust and efficient 3D shape representation.
Future Extensions#
The paper’s core contribution, CoFie, presents a novel, compact neural surface representation using coordinate fields. Future work could explore several promising avenues. Firstly, enhancing the model’s ability to handle complex topologies and intricate details would significantly broaden its applicability. This might involve incorporating techniques from mesh processing or more sophisticated implicit surface representations. Secondly, improving the efficiency of the Coordinate Field optimization process is crucial, particularly for large-scale shapes. This could involve investigating more advanced optimization algorithms or exploring alternative parameterizations. Thirdly, extending CoFie to handle dynamic shapes and deformations would open up exciting new applications, especially in computer animation and robotics. This would require mechanisms for tracking changes in geometry and updating the coordinate fields accordingly. Finally, it would be beneficial to investigate the potential of CoFie within broader shape analysis tasks, including shape matching, retrieval, and generation, to demonstrate its potential beyond shape representation itself. Such advancements would firmly establish CoFie’s versatility and impact within the computer graphics and machine learning communities.
More visual insights#
More on figures

🔼 This figure showcases the variety and quality of 3D shapes that the CoFie model can generate. It displays examples from three different sources: novel shapes from ShapeNet’s training categories, shapes from unseen ShapeNet categories, and real-world shapes from the Thingi dataset. The use of surface normals in the visualization helps to highlight the details and quality of the generated meshes. A more detailed comparison with ground truth is available in the appendix of the paper.
read the caption
Figure 3: Diveristy and quality of meshes that CoFie can represent. The results include both novel instances from ShapeNet training categories (top left), instances from ShapeNet unseen categories (bottom left), and real shapes from the Thingi dataset (right). We visualize the shapes with surface normal to better show their geometry. Please see the appendix for comparisons with ground-truth.
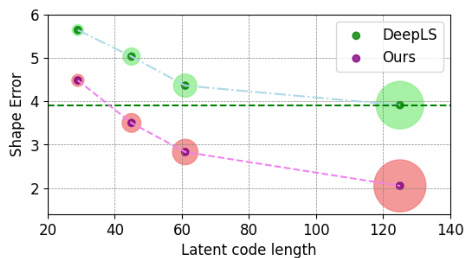
🔼 This figure shows the trade-off between the accuracy (measured by Chamfer distance) and model size (measured by latent code length) of CoFie and DeepLS on ShapeNet unseen categories. The size of the circles represents the latent code length, while the y-axis indicates the Chamfer distance, a measure of shape error. CoFie consistently outperforms DeepLS across all latent code lengths, demonstrating superior performance even with significantly fewer parameters. The dashed lines represent the average performance of each method.
read the caption
Figure 4: Trade-off between accuracy and model size (notified by the radius of circles).
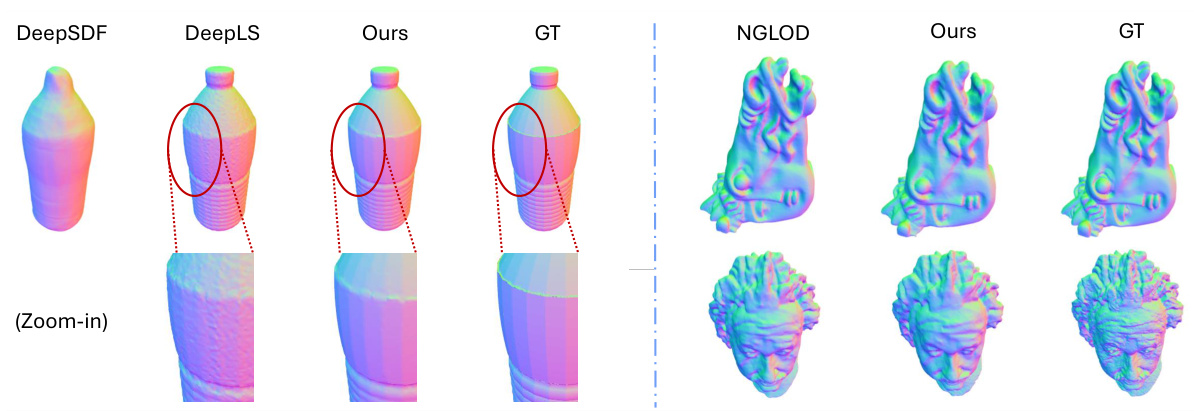
🔼 This figure compares the performance of CoFie against two other generalizable methods (DeepSDF and DeepLS) on ShapeNet shapes. For each shape, two views are shown: one providing a general overview of the shape and the second showing a zoomed-in portion to highlight details. The comparison visually demonstrates CoFie’s ability to better capture fine details compared to the other two methods.
read the caption
Figure 6: Compare with the generalizable methods DeepSDF and DeepLS on ShapeNet shapes. We show two images for each method, one for the overall shape quality, and a zoom-in detail check.

🔼 This figure compares the performance of CoFie against two other generalizable neural implicit surface representation methods, DeepSDF and DeepLS, on a set of ShapeNet shapes. For each shape and method, two views are shown: one providing an overall view of the shape and its quality, and another showing a zoomed-in view for more detailed analysis of specific regions. This visual comparison allows for a direct assessment of CoFie’s ability to represent fine geometric details in comparison to existing approaches.
read the caption
Figure 6: Compare with the generalizable methods DeepSDF and DeepLS on ShapeNet shapes. We show two images for each method, one for the overall shape quality, and a zoom-in detail check.
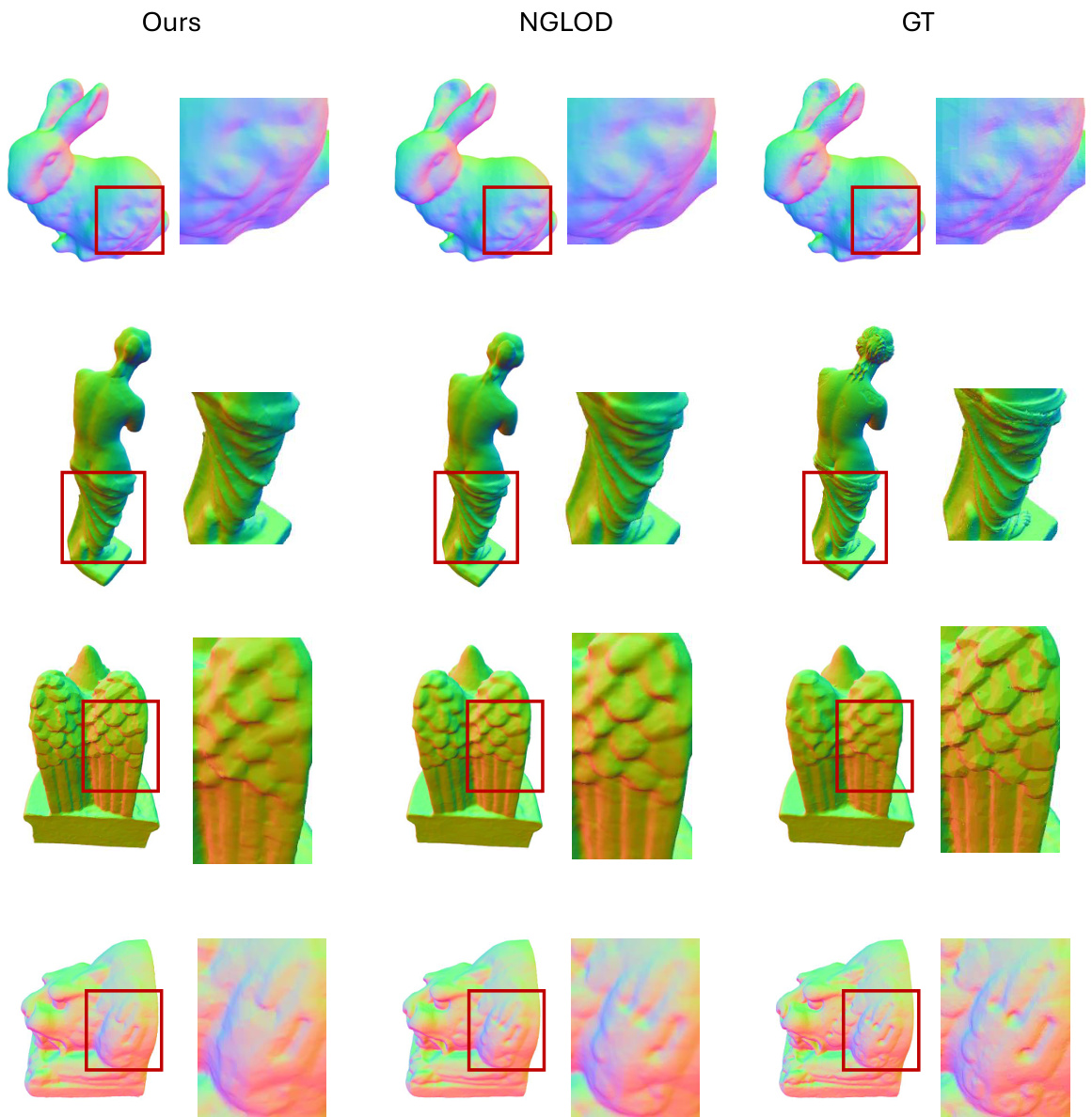
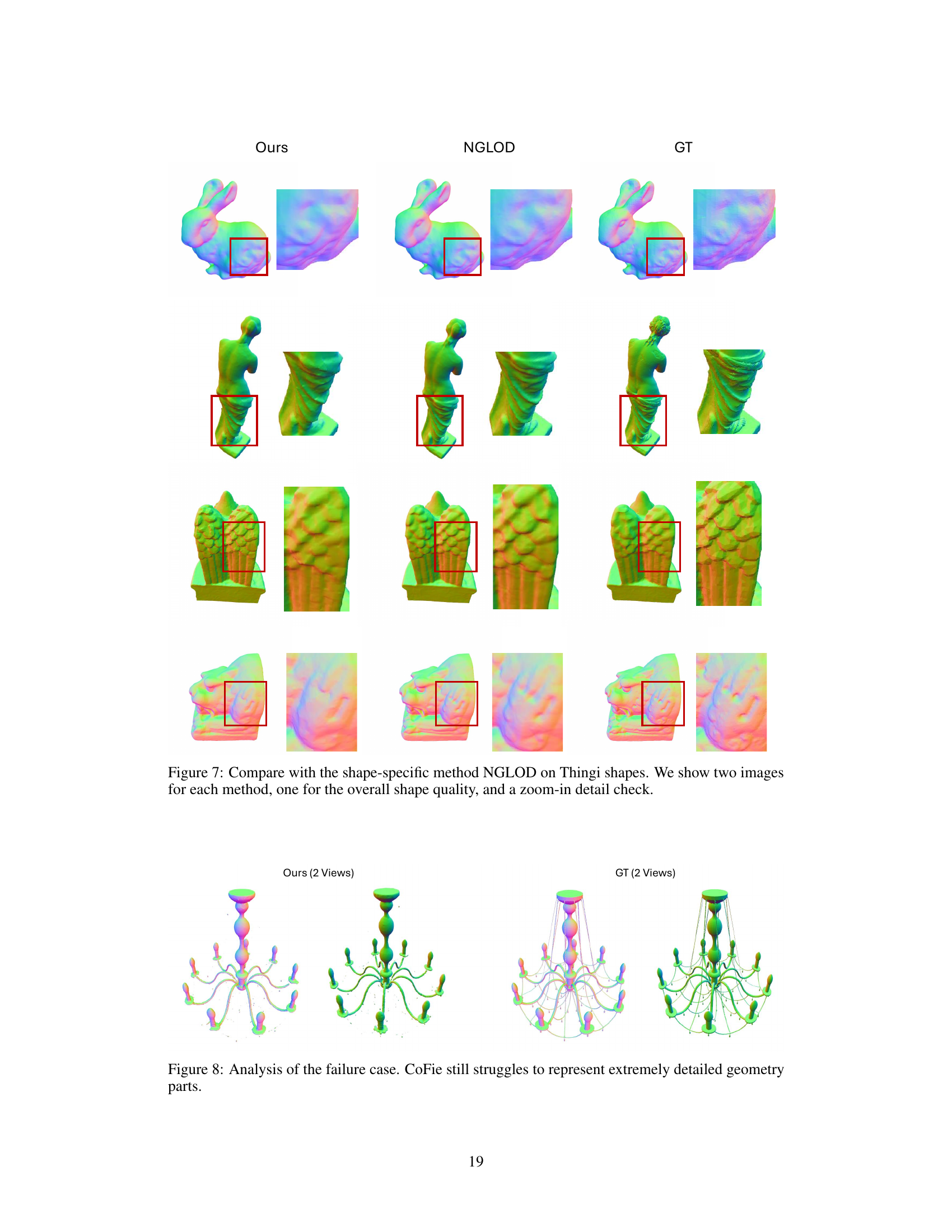
🔼 This figure compares the performance of CoFie against NGLOD, a shape-specific method, on the Thingi dataset of real-world shapes. For each shape (a rabbit, Venus de Milo statue, winged angel statue, and a lion head), it shows two views: one highlighting the overall reconstruction quality and a zoomed-in view to showcase the level of detail achieved. The comparison visually demonstrates CoFie’s ability to model complex geometries while using a single, shared MLP. This highlights CoFie’s generalizability, a key advantage over shape-specific methods.
read the caption
Figure 7: Compare with the shape-specific method NGLOD on Thingi shapes. We show two images for each method, one for the overall shape quality, and a zoom-in detail check.
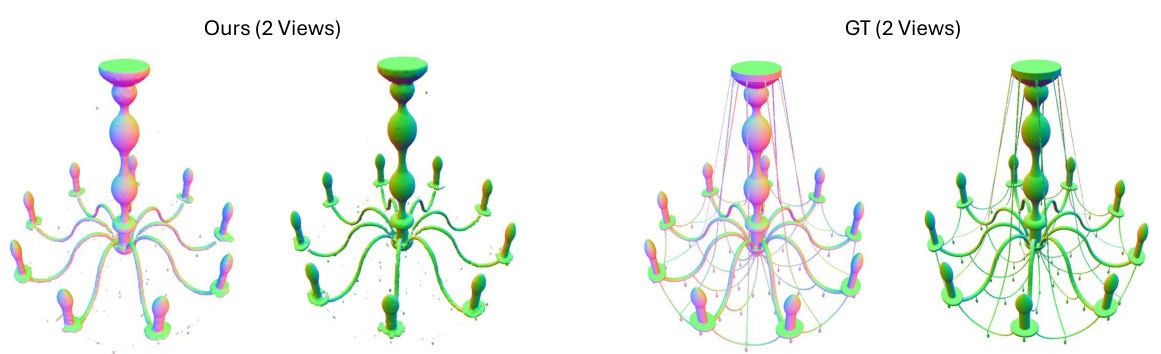
🔼 This figure shows a comparison between the model’s reconstruction (CoFie) and the ground truth for a complex chandelier model. The left side displays two views of the model generated by CoFie, highlighting areas where fine details, such as the intricate curvatures of the chandelier arms and the delicate structures of the light fixtures, were not accurately captured. The right side presents two views of the ground truth model, showcasing the level of detail that CoFie struggled to replicate. This illustrates a limitation of the CoFie model in representing extremely detailed geometry.
read the caption
Figure 8: Analysis of the failure case. CoFie still struggles to represent extremely detailed geometry parts.
More on tables
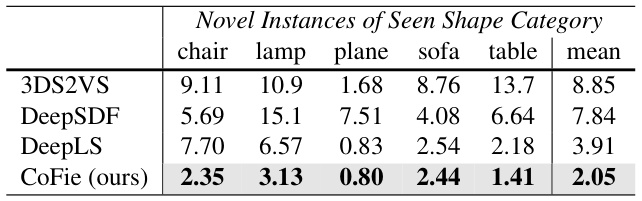
🔼 This table presents the quantitative results of the proposed CoFie method and three baseline methods (3DS2VS, DeepSDF, and DeepLS) on novel instances of seen shape categories from the ShapeNet dataset. The evaluation metric used is Chamfer distance, which measures the average distance between the reconstructed surface and the ground truth surface. The results are reported in units of 10-4, and the best performing method for each shape category is highlighted. The table shows that CoFie significantly outperforms other methods for all categories, achieving the lowest average Chamfer distance of 2.05.
read the caption
Table 1: Shape errors on novel instances of the ShapeNet training categories. We report chamfer distance (10-4) and highlight the best.

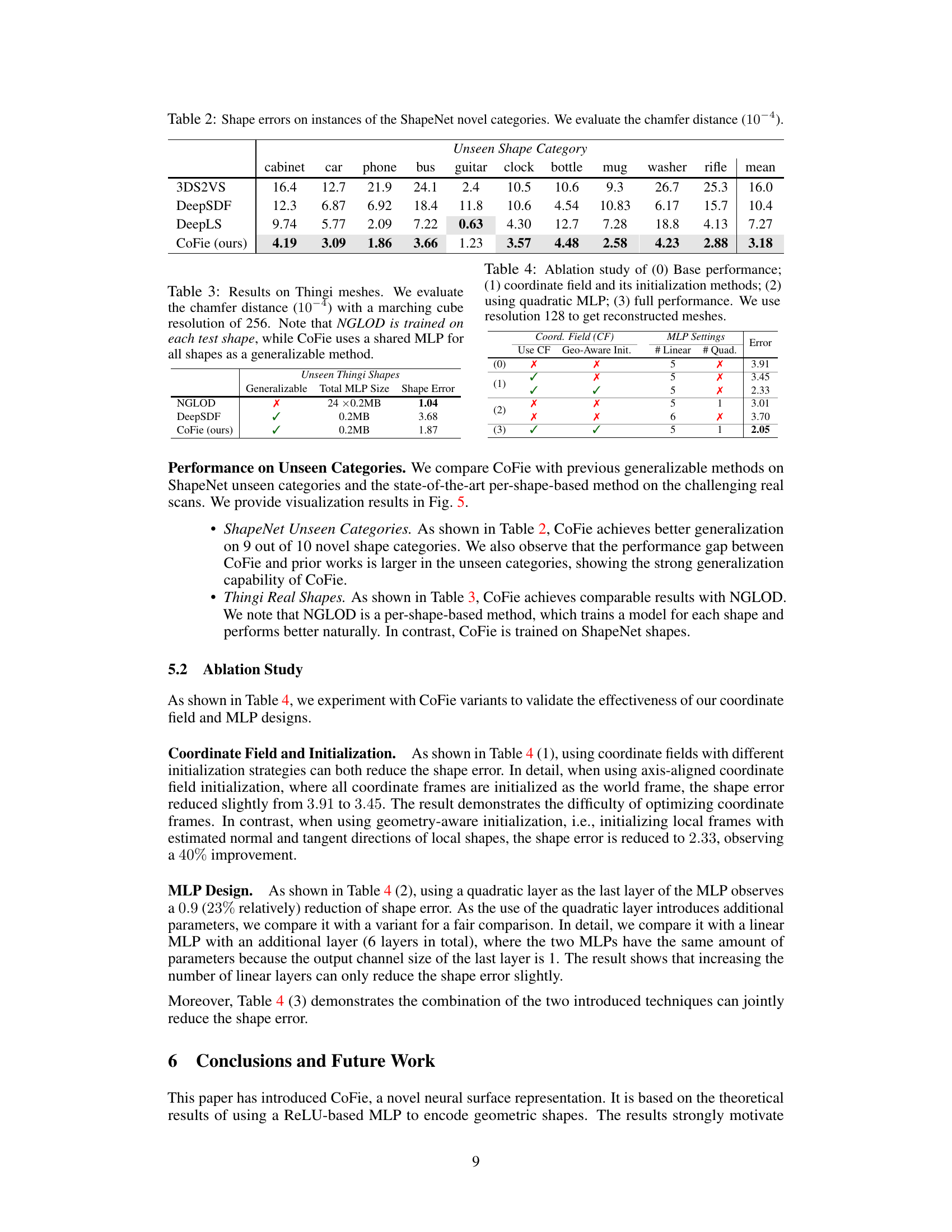
🔼 This table presents the Chamfer distance (a measure of shape similarity) for different shape reconstruction methods on unseen ShapeNet categories. Lower Chamfer distance indicates better reconstruction accuracy. The results are shown for 3DS2VS, DeepSDF, DeepLS and CoFie methods across ten different shape categories. This table demonstrates the generalization ability of the methods to unseen categories.
read the caption
Table 2: Shape errors on instances of the ShapeNet novel categories. We evaluate the chamfer distance (10-4).

🔼 This table presents the quantitative results of the CoFie model and baselines on the Thingi dataset. It shows the Chamfer distance (a measure of shape reconstruction error) achieved by different methods on unseen real-world shapes. Notably, it compares CoFie’s performance to a per-shape method (NGLOD), which is specifically trained for each shape in the test set, highlighting CoFie’s ability to generalize across different shapes using a single shared MLP.
read the caption
Table 3: Results on Thingi meshes. We evaluate the chamfer distance (10-4) with a marching cube resolution of 256. Note that NGLOD is trained on each test shape, while CoFie uses a shared MLP for all shapes as a generalizable method.
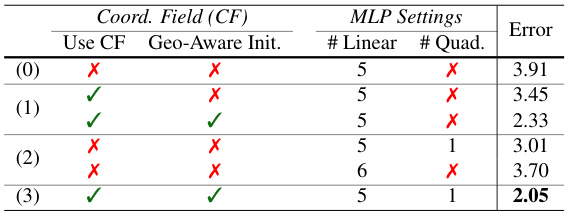
🔼 This ablation study demonstrates the impact of different components of CoFie on the shape reconstruction performance. It compares the base model with and without Coordinate Fields, geometric initialization for the Coordinate Fields, and the use of quadratic layers in the MLP. The table shows the chamfer distance error for each configuration.
read the caption
Table 4: Ablation study of (0) Base performance; (1) coordinate field and its initialization methods; (2) using quadratic MLP; (3) full performance. We use resolution 128 to get reconstructed meshes.
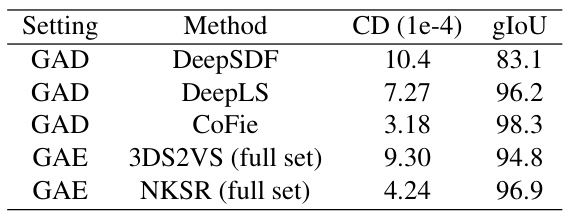
🔼 This table presents the performance comparison of CoFie against other methods on 10 unseen ShapeNet categories. It shows the Chamfer Distance (CD) and Intersection over Union (gIoU) scores. Note that 3DS2VS and NKSR were trained on the full ShapeNet dataset unlike CoFie, which used a subset of 1000 instances, making the comparison not entirely fair.
read the caption
Table 5: Performance on ShapeNet 10 novel categories. Specifically, the reported 3DS2VS [51] and NKSR [15] are trained on the full set of the training categories. In contrast, the reported numbers in the main paper use a subset of 1000 instances for training.
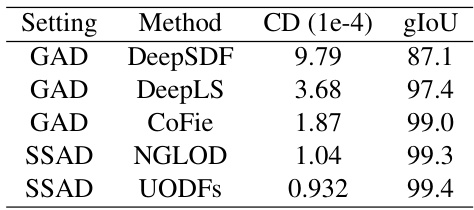
🔼 This table compares the performance of CoFie with other methods (DeepSDF, DeepLS, NGLOD, and UODFs) on the Thingi dataset. It shows Chamfer Distance (CD) and Intersection over Union (gIoU) metrics. The key takeaway is that CoFie achieves comparable performance to per-shape methods (SSAD), which are significantly more computationally expensive, while being significantly faster than generalizable methods (GAD).
read the caption
Table 6: Performance on Thingi shapes. Note that SSAD methods take a long time for inference, e.g. NGLOD and UODFs take 105 and 300 minutes, respectively. In contrast, CoFie takes 10 minutes.
Full paper#