TL;DR#
Reinforcement learning (RL) often struggles with the sim-to-real gap and sample inefficiency. Distributionally robust Markov decision processes (RMDPs) aim to address these by optimizing for the worst-case performance within an uncertainty set around a nominal model. However, the sample complexity of RMDPs, especially with general uncertainty measures, has remained largely unknown. This hinders their practical application and theoretical understanding.
This paper tackles this challenge by analyzing the sample complexity of RMDPs using generalized Lp norms as the uncertainty measure, under two common assumptions. The researchers demonstrate that solving RMDPs with general Lp norms can be more sample-efficient than solving standard MDPs. They achieve this by deriving near-optimal upper and lower bounds for the sample complexity, proving the tightness of their results. This work addresses a critical gap in the field, informing the design and analysis of more efficient and robust RL algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for reinforcement learning (RL) researchers because it significantly advances our understanding of sample complexity in distributionally robust RL, a critical area for bridging the sim-to-real gap and improving RL’s real-world applicability. The study of general Lp norms provides a broader framework for practical applications and theoretical investigations, and the findings challenge conventional wisdom about the efficiency of robust RL compared to standard RL. The paper opens new avenues for research by establishing near-optimal sample complexity bounds for solving robust Markov decision processes (RMDPs) using general smooth Lp norms.
Visual Insights#
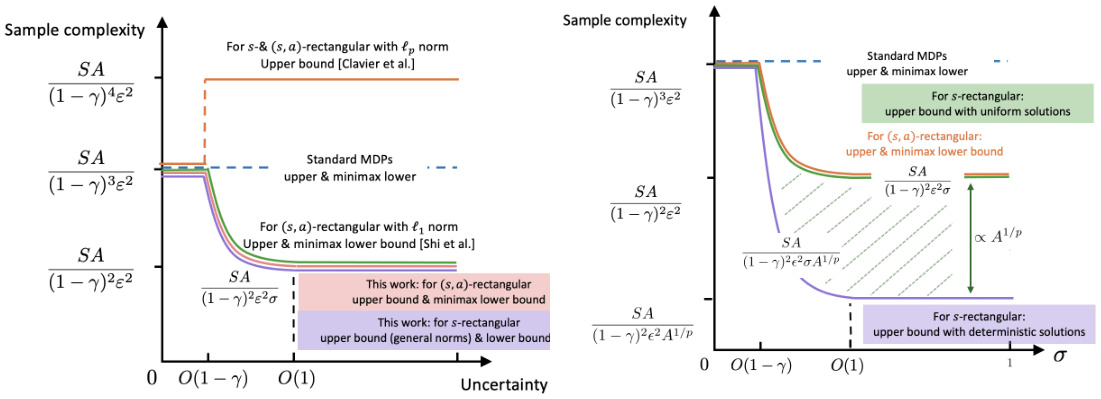
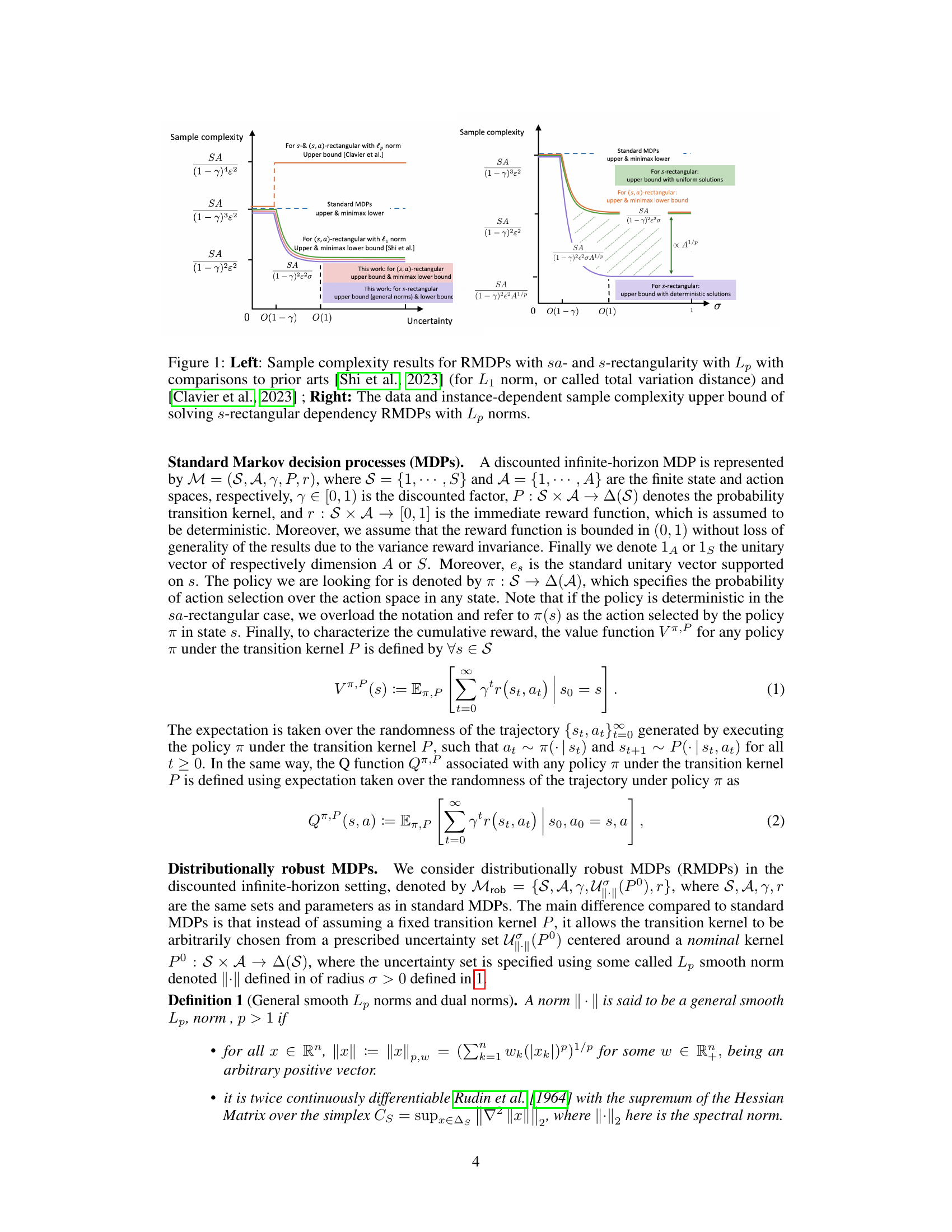
🔼 The figure compares the sample complexity of solving robust Markov Decision Processes (RMDPs) with different rectangularity assumptions (sa-rectangular and s-rectangular) and using general Lp norms. The left panel shows the sample complexity as a function of the uncertainty level (σ) for sa-rectangular and s-rectangular RMDPs, comparing the results with previous work using L1 norm (total variation distance). The right panel shows the instance-dependent sample complexity for s-rectangular RMDPs, illustrating the upper bound for general Lp norms and a lower bound for L∞ norm. Overall, the figure demonstrates the near-optimal sample complexity results obtained in this paper and the relationships between sa-rectangular and s-rectangular RMDPs.
read the caption
Figure 1: Left: Sample complexity results for RMDPs with sa- and s-rectangularity with Lp with comparisons to prior arts [Shi et al., 2023] (for L₁ norm, or called total variation distance) and [Clavier et al., 2023]; Right: The data and instance-dependent sample complexity upper bound of solving s-rectangular dependency RMDPs with Lp norms.
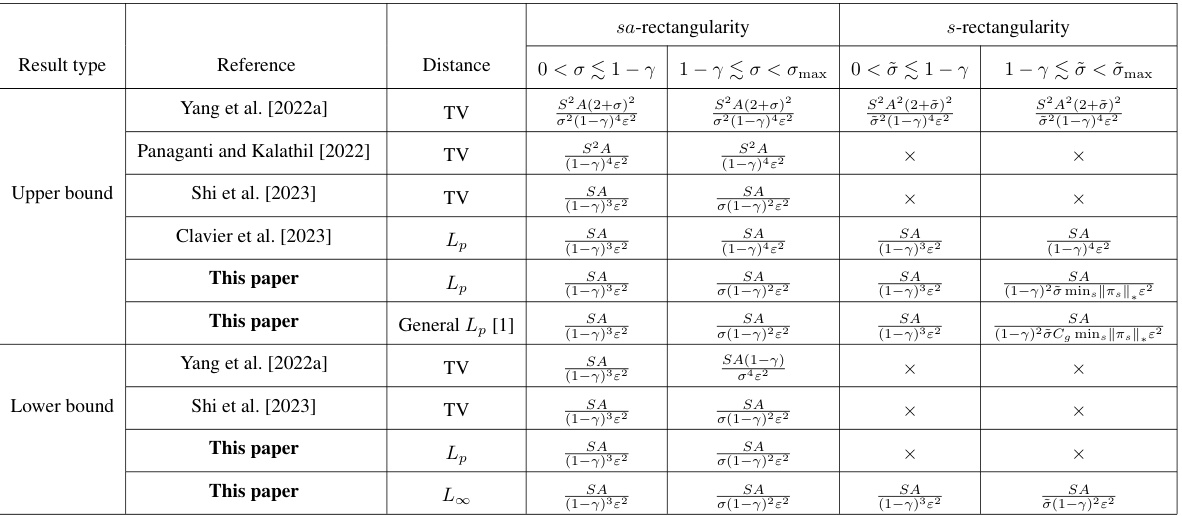
🔼 This table compares the sample complexity upper and lower bounds from this paper with those from several previous papers. The comparison is made across different distance functions (Total Variation, general Lp norms), and under both sa-rectangularity and s-rectangularity conditions. The results highlight the near-optimality of the new bounds derived in this work and show that solving distributionally robust reinforcement learning problems can be more sample efficient than solving standard RL problems in certain settings.
read the caption
Table 1: Comparisons with prior results (up to log terms) regarding finding an ɛ-optimal policy for the distributionally RMDP, where σ is the radius of the uncertainty set and max defined in Theorem 1.
Full paper#