TL;DR#
Transformer networks have achieved remarkable success in various sequence modeling tasks, yet their underlying mechanisms remain unclear. This paper tackles this challenge by providing a systematic study of the approximation properties of Transformers. It addresses key questions about the individual and combined effects of dot-product self-attention, positional encoding, and feed-forward layers. Previous studies have primarily relied on empirical analysis, lacking explicit theoretical understanding.
The researchers systematically analyze approximation rates of Transformers on sequence modeling tasks of varying complexity. Their theoretical analysis reveals the distinct roles of the number of layers, attention heads, and FFN width, highlighting the importance of appropriately balancing these components for optimal performance. The study also provides insights into the differences between attention and FFN layers and sheds light on the role of dot-product attention and positional encodings. These theoretical findings are validated through experiments and offer practical suggestions for improving the architecture of Transformer networks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning and sequence modeling because it provides a much-needed theoretical understanding of Transformer networks, a widely used architecture. It addresses the limitations of existing empirical studies by establishing explicit approximation rates for Transformer’s performance on various sequence modeling tasks. This theoretical foundation enables researchers to make better design choices when designing new Transformer-based models and improves our overall understanding of the architecture’s capabilities and limitations. The findings also offer valuable suggestions for alternative architectures and open new avenues for future research.
Visual Insights#

🔼 This table shows an example of the relative positional encoding used in the T5 Transformer model. The table illustrates how the function -r(t-s) maps the relative distance (t-s) between tokens t and s to a numerical value. For small distances (t-s < B), the encoding is linear, and for larger distances (B ≤ t-s < D), it decays logarithmically, showing the model’s handling of long-range dependencies.
read the caption
Table 1: An example of standard T5's Relative Positional Encoding
In-depth insights#
Transformer Power#
The concept of “Transformer Power” in the context of a research paper likely refers to the model’s capacity for sequence modeling, particularly its ability to handle long-range dependencies and complex relationships within sequences. A comprehensive analysis would explore several key aspects. Approximation properties would examine how well the transformer architecture can approximate complex functions within the sequence domain. The influence of critical hyperparameters like the number of layers, attention heads, and the feed-forward network width is crucial to understanding how these choices affect the transformer’s power. The mechanisms underpinning the transformer’s expressivity need to be investigated, including the role of self-attention, positional encoding, and residual connections, and how they interact to create the overall capabilities. A discussion of approximation rates, quantifying the efficiency of approximation with respect to model complexity, would provide further insights. Finally, comparing the transformer’s performance to alternative architectures on various sequence modeling tasks (e.g., fixed vs. adaptive memory) will showcase its strengths and weaknesses. Theoretical analysis, supported by empirical evidence, is key to establishing the foundation of “Transformer Power”.
Attn Mechanisms#
Attention mechanisms are fundamental to modern deep learning, particularly within sequence models like Transformers. Self-attention, a key component, allows the model to weigh the importance of different parts of the input sequence when processing each element. This is crucial for capturing long-range dependencies and contextual information, which traditional recurrent networks struggle with. Multi-head attention extends this concept by utilizing multiple attention heads, each focusing on different aspects or representations of the input. This enables the model to learn diverse relationships within the data. Different attention mechanisms have varying computational complexities and strengths. Dot-product attention is commonly used for its efficiency but has limitations regarding memory capacity for very long sequences. Alternatives such as linear attention mechanisms attempt to mitigate this computational bottleneck. Furthermore, the design and implementation of attention also impact performance. Relative positional encodings, for instance, provide additional context about the position of words without relying on absolute word positions which helps address issues with sequence length variability. The choice of attention mechanism and its associated components heavily influence a model’s capacity to process long and complex sequences and understand rich contextual relationships within the data.
RPE Efficiency#
Analyzing the efficiency of Relative Positional Encoding (RPE) in transformer models reveals crucial insights into their ability to handle long-range dependencies. RPE’s primary role is approximating memory kernels, efficiently capturing correlations between tokens separated by significant distances. The choice of RPE type significantly impacts performance; logarithmic RPEs excel with heavy-tailed memories, exhibiting superior performance in tasks requiring generalization across varying sequence lengths. Conversely, linear RPEs are better suited for light-tailed memories, demonstrating higher efficiency when dealing with shorter-range dependencies. Therefore, selecting the appropriate RPE is critical for optimal performance, and the choice should be guided by the specific characteristics of the data and the task’s demands. Further research could explore the development of adaptive RPE methods that dynamically adjust their behavior based on the input sequence’s properties, optimizing efficiency for diverse sequence modeling tasks.
DP Necessity#
The concept of “DP Necessity” in the context of transformer networks centers on the crucial role of the dot-product (DP) mechanism within the self-attention layer. The paper likely investigates whether DP is strictly necessary for achieving high performance, particularly in complex sequence modeling tasks. Initial analysis might suggest that alternative attention mechanisms could potentially substitute DP, perhaps offering computational advantages. However, the paper’s findings likely reveal nuances. While simpler tasks might not require DP’s power, more complex scenarios, like those involving intricate interdependencies between memory elements, may crucially benefit from the non-linearity and expressive capacity DP provides. The core argument likely highlights a trade-off: simpler tasks benefit from computationally efficient alternatives, while sophisticated tasks necessitate DP’s strengths for superior performance. Therefore, the paper’s contribution likely involves a more nuanced understanding of DP’s role, rather than simply declaring it essential or obsolete. The investigation likely also explores the impact of DP in conjunction with other components, such as positional encoding, to shed light on its combined effects on model expressivity.
Future Work#
The paper’s ‘Future Work’ section would ideally delve into several crucial areas. Expanding the theoretical framework to encompass more complex sequence modeling tasks, such as those involving intricate dependencies between tokens or varying memory structures, is essential. This could involve exploring alternative attention mechanisms or positional encoding schemes. Addressing the limitations of the current approximation rate analyses is another key direction. While the paper provides valuable bounds, exploring tighter approximation guarantees, particularly for scenarios with longer or less sparse memories, would significantly strengthen the theoretical contributions. Investigating the training dynamics of Transformers is also a critical area for future research. The paper’s analysis focuses on the expressiveness of Transformer architectures, but the learning process itself deserves further study, potentially involving analysis of training phases, optimization landscapes, and the evolution of attention weights over time. Finally, bridging theory and practice more effectively is crucial. Further experiments, particularly those on large language models or more complex real-world tasks, would help validate the theoretical insights and guide future model designs. Investigating the practical impact of model architectural choices, guided by theoretical insights, would be of significant value.
More visual insights#
More on tables

🔼 This table presents the results of an experiment designed to validate the first insight (1a) from the paper. The experiment compares the performance of Transformer models with varying numbers of layers (L) and attention heads (H) on a language modeling task. The results show that increasing the number of layers (L) significantly reduces the validation loss, while increasing the number of attention heads (H) has a much smaller effect. The number of parameters in each model is roughly balanced, allowing a fair comparison.
read the caption
Table 2: Results of the experiment supporting Insight (1a).

🔼 The table shows the final validation losses for learning a sparse Boolean function with different numbers of attention heads (H) and FFN width (m). The results support the insight that a single-layer Transformer with sufficient H and m can effectively model such a function, without needing additional layers.
read the caption
Table 3: Results of the experiment supporting Insight (1b).

🔼 This table presents the results of an experiment designed to validate Insight 2a of the paper. Insight 2a posits that for tasks involving a complex readout function and simple memories, increasing the FFN width (m) significantly improves performance, while increasing the number of attention heads (H) has little to no effect. The table shows the final validation loss for different combinations of H and m, demonstrating the significant performance gain achieved by increasing m and the negligible effect of increasing H.
read the caption
Table 4: Results of the experiment supporting Insight (2a).
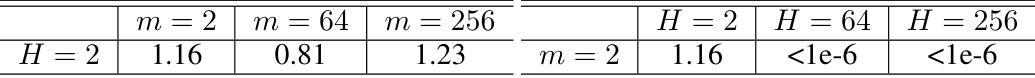
🔼 This table presents the results of an experiment designed to validate the hypothesis that for tasks with memories lacking intricate interrelationships (Type I), single-layer Transformers with sufficient Attn heads and FFN width suffice. The experiment involved training single-layer DP-free Transformers with varying numbers of attention heads (H) and FFN widths (m) to learn a sparse Boolean target function. The validation loss is reported for each configuration, demonstrating that a single-layer model can achieve low loss with sufficient width and head count.
read the caption
Table 3: Results of the experiment supporting Insight (1b).

🔼 This table presents the final validation loss for learning a sparse Boolean function with a simple readout function and simple memories. The experiment compared the performance of single-layer DP-free transformers with different numbers of attention heads (H) and FFN widths (m), both with and without the dot product (DP) structure in the attention layer. The results show that a single-layer DP-free transformer with sufficient H and m can effectively learn this sparse Boolean function, and the inclusion of DP provides only a minor improvement in performance.
read the caption
Table 6: Results of the experiment supporting Insight (3a).

🔼 This table presents the final validation losses for Transformer models with and without the dot-product (DP) structure in the attention layer. The results show that, for NLP pre-training tasks, Transformer models incorporating DP structure achieve lower validation losses than DP-free Transformer models, thus supporting the necessity of DP in achieving higher performance for complex NLP tasks.
read the caption
Table 7: Results of the experiment supporting Insight (3b).
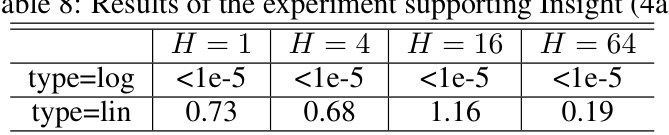
🔼 This table presents the final validation losses for learning heavy-tailed memories using single-layer, FFN-free, DP-free Transformers with log-type RPE or lin-type RPE and varying numbers of attention heads. The results show that for heavy-tailed memories, even a single-head Transformer with log-type RPE performs well, while lin-type RPE shows limited improvement even with many heads.
read the caption
Table 8: Results of the experiment supporting Insight (4a)

🔼 This table presents the results of an experiment designed to validate Insight (4a) of the paper. The experiment focuses on evaluating the performance of Transformers with different types of relative positional encoding (RPE) for sequence modeling tasks involving heavy-tailed memories. The results show that Transformers with log-type RPE achieve significantly better performance than those with lin-type RPE, even with a small number of attention heads. This supports the claim that log-type RPE is more efficient for handling heavy-tailed memories.
read the caption
Table 8: Results of the experiment supporting Insight (4a).
Full paper#



















