TL;DR#
Large language models (LLMs) are increasingly used in high-stakes applications, raising concerns about the lack of transparency in their decision-making processes. Understanding how LLMs manage uncertainty is essential for safe and effective deployment. Prior research has focused on quantifying and calibrating model confidence, but the internal mechanisms LLMs employ remain largely unexplored. This study addresses this gap by investigating two crucial components: entropy neurons and token frequency neurons.
This paper identifies and analyzes these two neuron types, showing how they regulate uncertainty in LLMs’ next-token predictions. Entropy neurons subtly modulate the output distribution’s entropy by influencing the final layer normalization, leading to changes in confidence with minimal direct effect on the prediction itself. Token frequency neurons adjust each token’s logit proportionally to its frequency, shifting the output distribution towards or away from the unigram distribution. The researchers demonstrate the effectiveness of these neurons in managing confidence across various models, including in the context of induction tasks. This work provides valuable insights into the internal workings of LLMs and contributes to our understanding of how they handle uncertainty.
Key Takeaways#
Why does it matter?#
This paper is crucial because it sheds light on the internal mechanisms of large language models (LLMs), specifically how they manage uncertainty in their predictions. This understanding is vital for improving LLM development, ensuring safe deployment, and advancing research on model interpretability and calibration. It also opens new avenues for research, such as exploring the role of specific neuron types in various tasks and contexts.
Visual Insights#
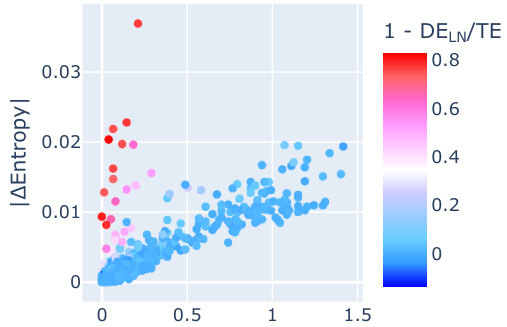
🔼 This figure shows the relationship between the change in entropy and the change in prediction after ablating (removing) individual neurons in the final layer of a language model. Each point represents a neuron. The x-axis shows how much the model’s prediction changes after the neuron is ablated, and the y-axis represents the change in the model’s output entropy. Red points highlight neurons whose effect is mediated by Layer Normalization, demonstrating that they influence confidence without significantly altering the model’s prediction. This suggests the presence of specialized neurons influencing model uncertainty.
read the caption
Figure 1: Entropy and Prediction. We mean ablate final-layer neurons across 4000 tokens and measure the variation in the entropy of the model's output Pmodel against average change of model's prediction (argmax Pmodel(x)). We identify a set of neurons whose effect depends on LayerNorm (red points; metric described in §3.2), and which affect the model's confidence (quantified as entropy of Pmodel) with minimal impact on the prediction.
In-depth insights#
LLM Uncertainty#
Large language model (LLM) uncertainty is a crucial area of research, impacting model reliability and trustworthiness. Calibration, the agreement between predicted probabilities and actual accuracy, is a key aspect. Poorly calibrated LLMs can be overconfident, leading to inaccurate predictions and potentially harmful consequences. Understanding the mechanisms LLMs use to represent and regulate uncertainty is vital for improving their performance and safety. Internal mechanisms, such as the recently discovered ’entropy neurons’ and ’token frequency neurons’, are being investigated to shed light on how LLMs manage uncertainty. These neurons appear to modulate confidence by influencing the output distribution, adjusting it towards or away from the unigram distribution, depending on the situation’s uncertainty level. Future research should focus on further investigating these mechanisms and exploring additional factors that contribute to LLM uncertainty, ultimately aiming to build more reliable and robust models.
Entropy Neuron Roles#
The concept of ‘Entropy Neuron Roles’ in large language models (LLMs) centers on how these specialized neurons manage uncertainty and model confidence. Entropy neurons appear to calibrate model predictions by subtly influencing the output distribution’s entropy, primarily through interaction with LayerNorm rather than directly manipulating logits. This nuanced mechanism allows them to modulate confidence without significantly affecting the model’s primary predictions. Further investigation suggests a connection between entropy neurons and the unembedding matrix’s null space, indicating a sophisticated learning strategy. The impact is evident during inductive tasks where repeated sequences are detected, with entropy neurons actively managing the model’s confidence levels. While research continues to explore their specific behavior, entropy neurons represent a crucial mechanism in LLMs for controlling prediction certainty and mitigating potential overconfidence risks.
Frequency Neuron Discovery#
The discovery of “frequency neurons” represents a significant advancement in understanding how large language models (LLMs) manage uncertainty. These neurons, unlike previously identified entropy neurons, directly modulate a token’s logit in proportion to its frequency in the training data. This mechanism suggests a calibration strategy where LLMs actively adjust their output distribution to align more closely with the unigram distribution in uncertain situations. This finding is particularly insightful as it reveals an internal mechanism explicitly linking token probability to their frequency, offering a novel perspective on LLM confidence and calibration. The discovery opens up new avenues for research into more nuanced methods for managing LLM uncertainty and improving model performance, particularly in situations where high confidence is unwarranted.
Induction Case Study#
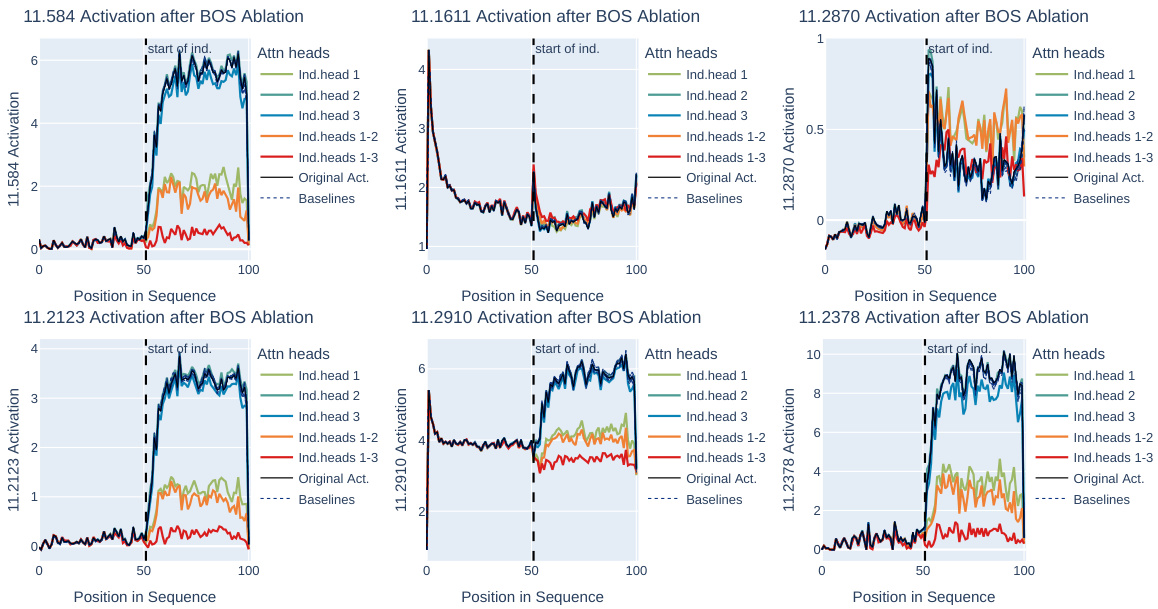
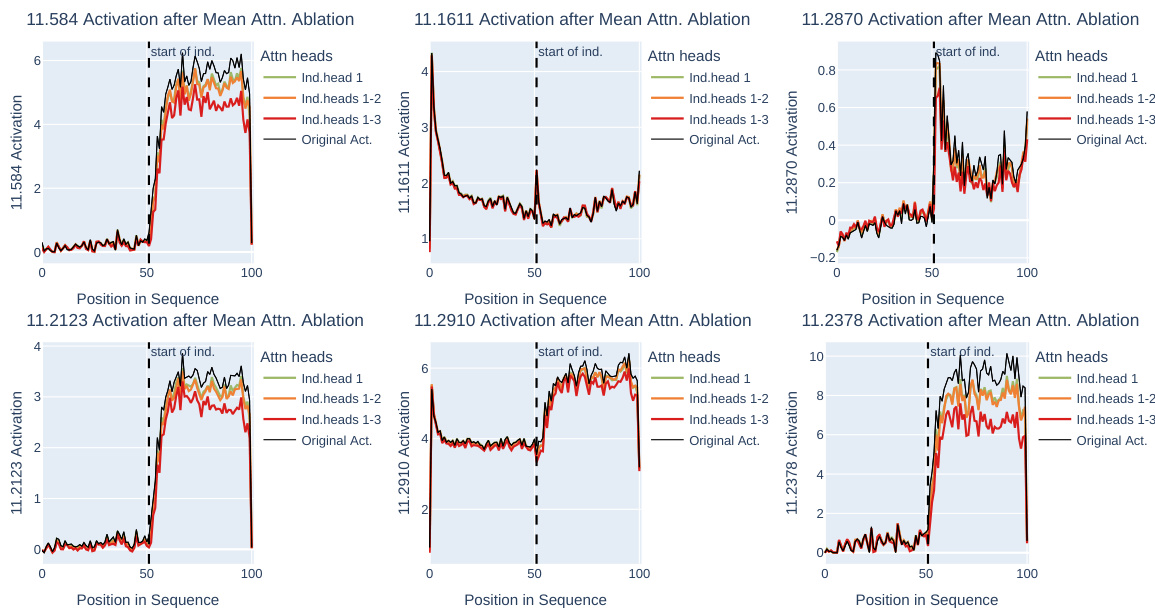
The induction case study section delves into how the model handles repeated subsequences, a phenomenon called induction. The authors investigate how entropy neurons actively manage confidence in this setting, increasing the entropy (uncertainty) of the output distribution during induction to mitigate confidently incorrect predictions. This hedging mechanism prevents the model from making large prediction errors when the model becomes too confident. They also examine the activation patterns of neurons in scenarios with repeated sequences. The results showcase the dynamic interplay between entropy neurons and induction heads, specialized attention mechanisms responsible for handling inductive reasoning in the model. This highlights the sophisticated internal mechanisms models use to regulate confidence and improve calibration, especially in ambiguous situations.
Future Research#
Future research should investigate the broader implications of confidence regulation mechanisms in LLMs. This includes exploring diverse tasks beyond next-token prediction, such as question-answering and reasoning, to determine the generalizability of the findings. Understanding the interplay between different neural components and their impact on uncertainty management is crucial. Further research should examine the relationship between architecture, training data, and the emergence of confidence-regulating neurons. A key focus should be to determine how different models, particularly those trained with varying amounts of data and diverse architectures, implement confidence calibration. Finally, rigorous investigation into the robustness of these mechanisms to adversarial attacks and various training paradigms is essential for safe and reliable deployment of LLMs.
More visual insights#
More on figures

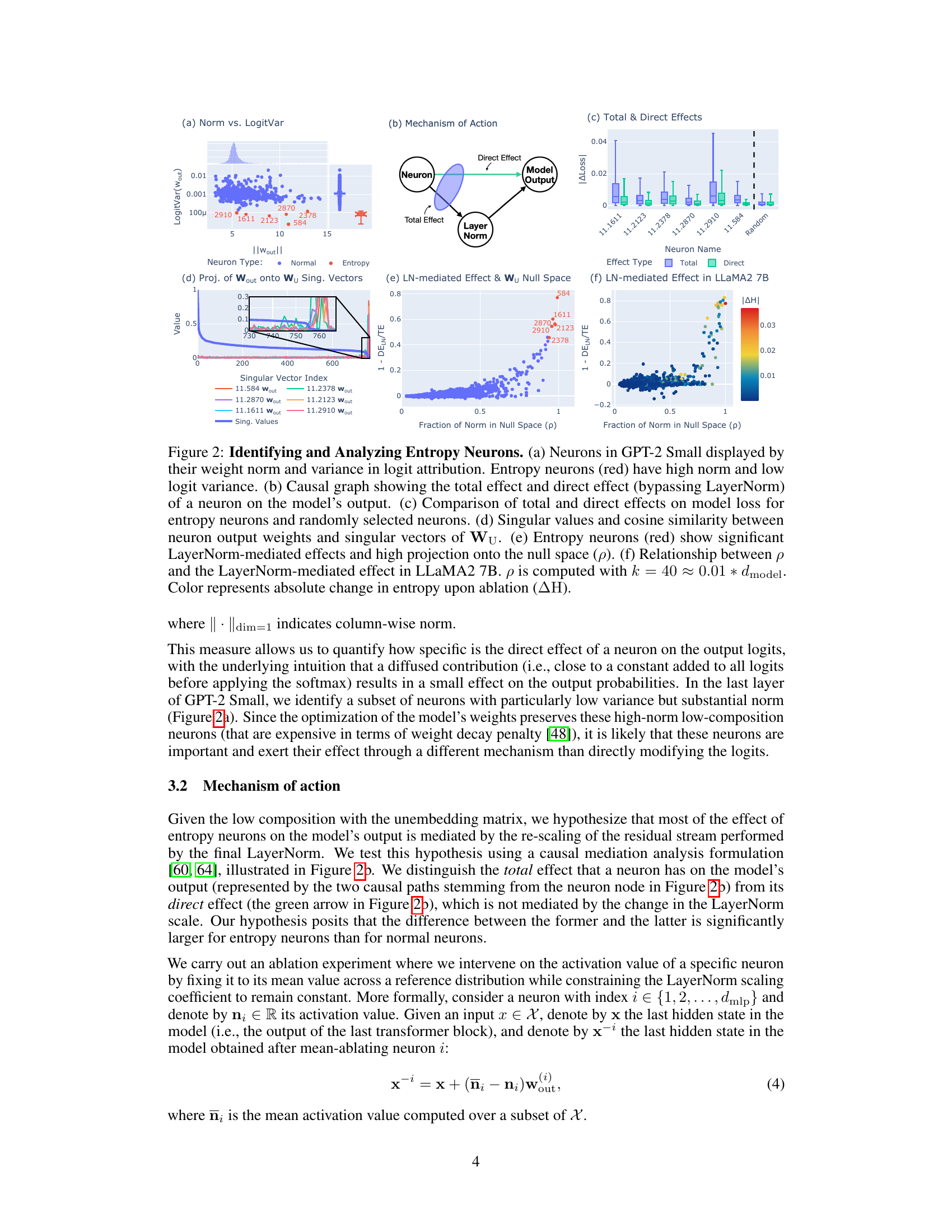
🔼 This figure analyzes entropy neurons, a type of neuron with high weight norm and low composition with the unembedding matrix. Panel (a) shows the relationship between weight norm and logit variance, identifying entropy neurons. Panel (b) presents a causal graph illustrating the total and direct effects of a neuron on the model output, mediated by LayerNorm. Panel (c) compares these effects for entropy neurons versus randomly selected neurons. Panel (d) shows the projection of neuron output weights onto the singular vectors of the unembedding matrix, indicating a high projection onto the null space for entropy neurons. Panel (e) demonstrates the significant LayerNorm-mediated effects of these neurons and their high projection onto the null space. Finally, panel (f) shows the same relationship in the LLaMA2 7B model.
read the caption
Figure 2: Identifying and Analyzing Entropy Neurons. (a) Neurons in GPT-2 Small displayed by their weight norm and variance in logit attribution. Entropy neurons (red) have high norm and low logit variance. (b) Causal graph showing the total effect and direct effect (bypassing LayerNorm) of a neuron on the model's output. (c) Comparison of total and direct effects on model loss for entropy neurons and randomly selected neurons. (d) Singular values and cosine similarity between neuron output weights and singular vectors of Wu. (e) Entropy neurons (red) show significant LayerNorm-mediated effects and high projection onto the null space (p). (f) LN-mediated effect in LLaMA2 7B. p is computed with k = 40 ≈ 0.01 * dmodel. Color represents absolute change in entropy upon ablation (ΔΗ).
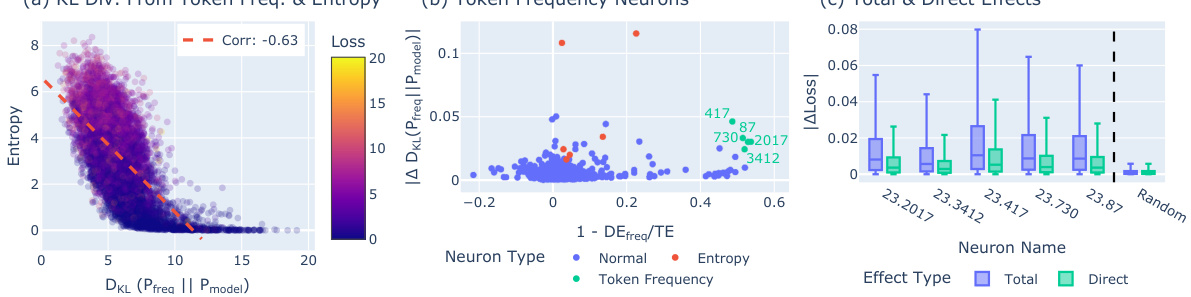
🔼 This figure analyzes token frequency neurons in the Pythia 410M language model. Panel (a) shows a negative correlation between the KL divergence from the token frequency distribution (DKL) and entropy, indicating that as model uncertainty increases (higher entropy), the model’s output distribution becomes closer to the token frequency distribution. Panel (b) is a scatter plot showing the relationship between a neuron’s effect on DKL and the mediation effect via the token frequency direction. Token frequency neurons, highlighted in green, show a substantial mediation effect. Finally, panel (c) uses box plots to show that the total effect of token frequency neurons (on model loss) is significantly different from their direct effect, suggesting that these neurons impact confidence primarily through modulation of the token frequency distribution.
read the caption
Figure 3: Token Frequency Neurons in Pythia 410M. (a) DKL(Pfreq||Pmodel) and Entropy are correlated negatively. (b) Scatter plot of neurons highlighting token frequency neurons (in green), with high effect on DKL(Pfreq||Pmodel), significantly mediated by the token frequency direction. (c) Box plots showing substantial difference in total vs. direct effect in token frequency neurons.
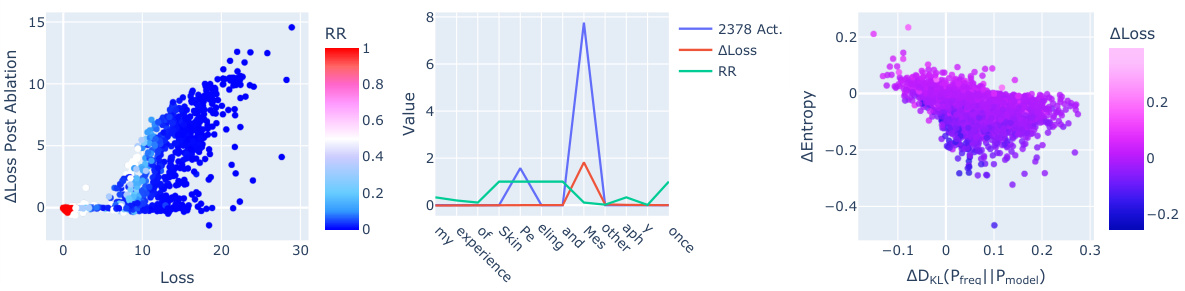
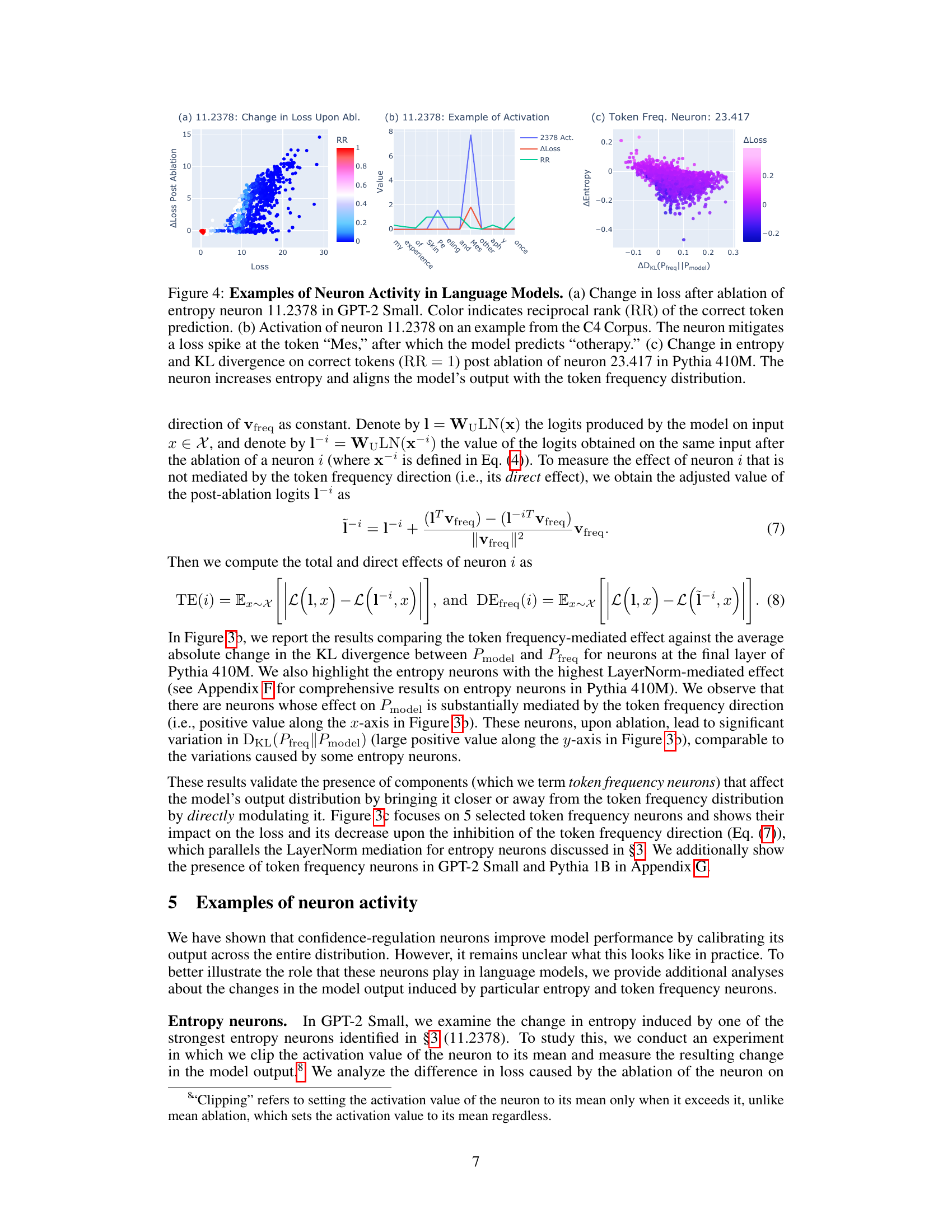
🔼 This figure shows three subplots illustrating the activity of specific neurons in language models. Subplot (a) demonstrates the impact of ablating entropy neuron 11.2378 in GPT-2 Small on model loss, color-coded by the reciprocal rank of the correct prediction. Subplot (b) shows the activation pattern of the same neuron on a specific example from the C4 corpus, highlighting its role in mitigating a loss spike. Finally, subplot (c) displays the effect of ablating token frequency neuron 23.417 in Pythia 410M on entropy and KL divergence for correctly predicted tokens, indicating its influence on model confidence and alignment with the token frequency distribution.
read the caption
Figure 4: Examples of Neuron Activity in Language Models. (a) Change in loss after ablation of entropy neuron 11.2378 in GPT-2 Small. Color indicates reciprocal rank (RR) of the correct token prediction. (b) Activation of neuron 11.2378 on an example from the C4 Corpus. The neuron mitigates a loss spike at the token “Mes,” after which the model predicts “otherapy.” (c) Change in entropy and KL divergence on correct tokens (RR = 1) post ablation of neuron 23.417 in Pythia 410M. The neuron increases entropy and aligns the model’s output with the token frequency distribution.
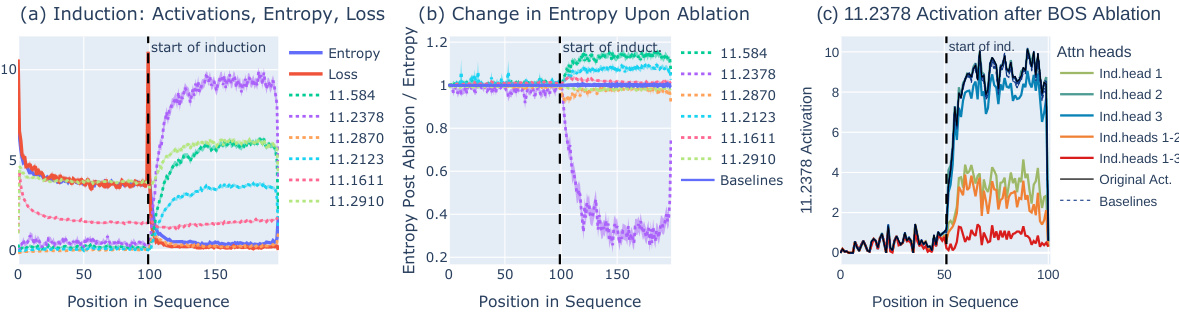
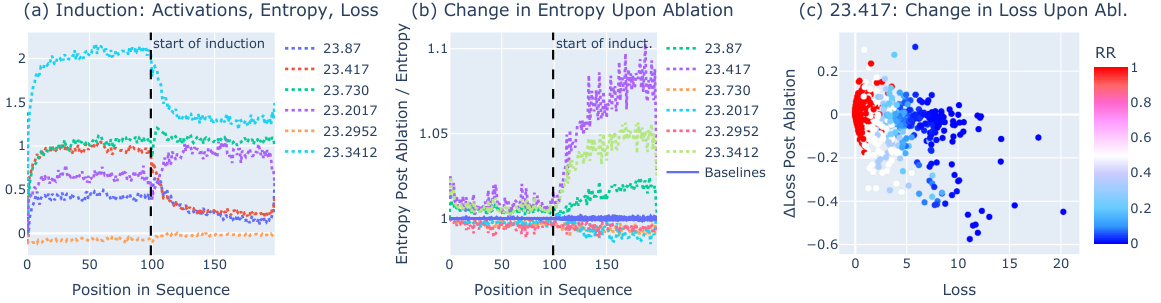
🔼 This figure shows the results of experiments on induction, which is the repetition of subsequences in the input. Panel (a) displays activations, entropy, and loss across duplicated 200-token input sequences. Panel (b) demonstrates the impact of selectively turning off (‘ablating’) specific entropy neurons; particularly, neuron 11.2378 shows a significant reduction in entropy (up to 70%). Finally, panel (c) illustrates the effect of removing (‘ablating’) induction heads on the activation of neuron 11.2378, revealing a substantial decrease in its activation.
read the caption
Figure 5: Entropy Neurons on Induction. (a) Activations, entropy, and loss across duplicated 200-token input sequences. (b) The effect of clip mean-ablation of specific entropy neurons. Neuron 11.2378 shows the most significant impact, with up to a 70% reduction in entropy. (c) BOS ablation of induction heads: Upon the ablation of three induction heads in GPT-2 Small, the activation of entropy neuron 11.2378 decreases substantially.
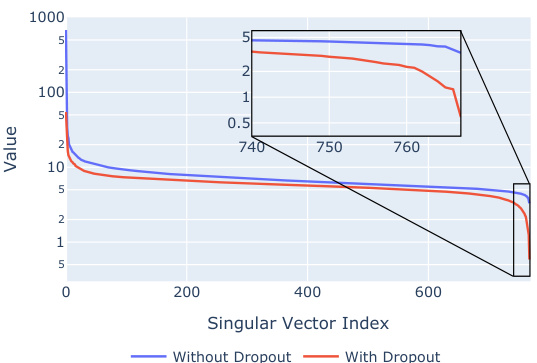
🔼 This figure shows the singular values of the unembedding matrix (Wu) for two versions of the Pythia 160M model. One model was trained with dropout, and the other was trained without dropout. The singular values represent the importance of different dimensions in the vocabulary space. The sharp drop in singular values for both models indicates the presence of an effective null space in the unembedding matrix. The model trained with dropout has smaller singular values, especially in the lower dimensions, which is consistent with the hypothesis that dropout encourages the creation of a null space. This null space is where entropy neurons operate, and the low singular values suggest that the model is deliberately restricting the capacity of its representation by making certain dimensions of the residual stream have minimal effect on the final logits.
read the caption
Figure 6: Effect of Dropout on Wu. Comparison of singular values for the unembedding matrix between two versions of Pythia 160M—one trained with dropout (red) and one without dropout (blue).
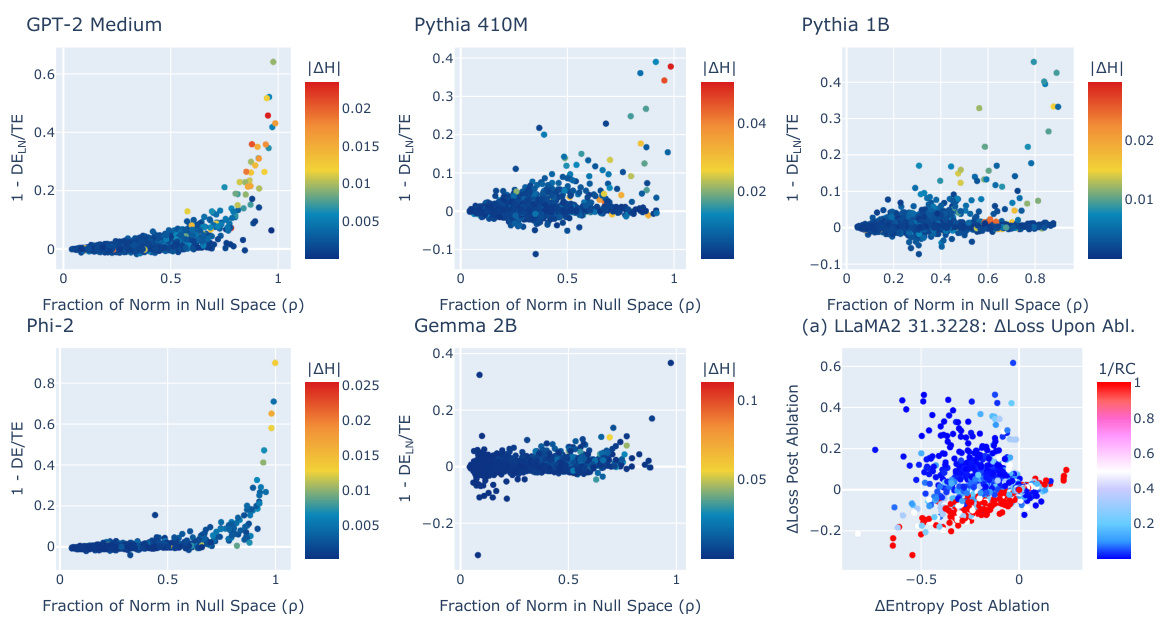
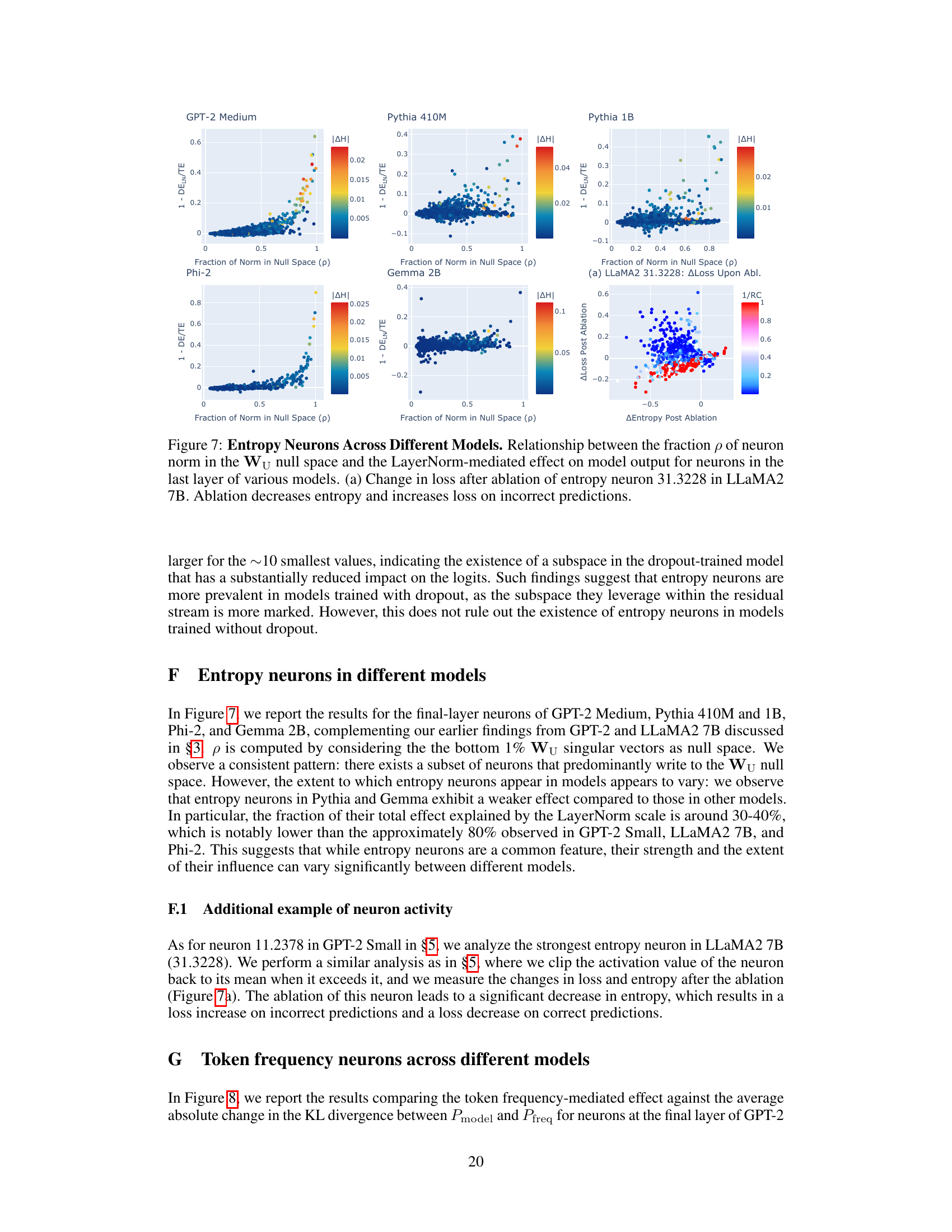
🔼 This figure shows the relationship between the fraction of a neuron’s norm that lies in the null space of the unembedding matrix (p) and the LayerNorm-mediated effect on the model’s output for neurons in the last layer of several different language models. The color of each point represents the magnitude of the change in entropy after ablating the neuron. The figure also shows a case study where ablating an entropy neuron in LLaMA2 7B decreases the entropy of the output distribution and increases the loss on incorrect predictions. This demonstrates that entropy neurons modulate confidence by impacting the LayerNorm, a mechanism that may be overlooked by other methods of analysis that focus solely on the logits.
read the caption
Figure 7: Entropy Neurons Across Different Models. Relationship between the fraction p of neuron norm in the Wu null space and the LayerNorm-mediated effect on model output for neurons in the last layer of various models. (a) Change in loss after ablation of entropy neuron 31.3228 in LLaMA2 7B. Ablation decreases entropy and increases loss on incorrect predictions.
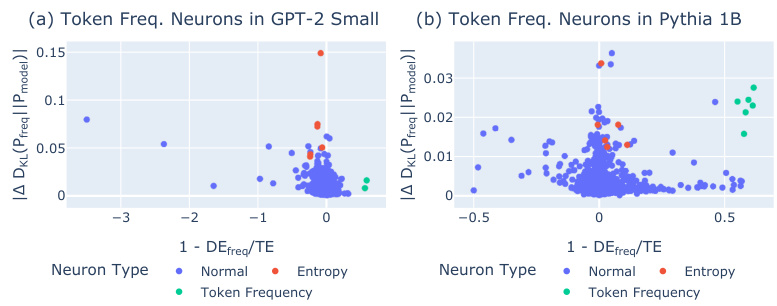
🔼 This figure shows the relationship between the effect of token frequency neurons and the change in KL divergence from the unigram distribution for GPT-2 Small and Pythia 1B. Each point represents a neuron, colored according to its type: normal, entropy, or token frequency. The x-axis represents the fraction of the neuron’s total effect that is not mediated by the token frequency direction. The y-axis represents the average absolute change in KL divergence from the unigram distribution after ablating the neuron. It illustrates how token frequency neurons modulate the model’s output distribution’s proximity to the unigram distribution, particularly in relation to entropy neurons and normal neurons.
read the caption
Figure 8: Token Frequency Neurons Across Different Models. Relationship between the token frequency-mediated effect and the average absolute change in the KL divergence from Pfreq for final-layer neurons in (a) GPT-2 Small and (b) Pythia 1B. Neurons are categorized as normal, entropy, or token frequency neurons.

🔼 This figure shows the results of experiments designed to investigate the role of entropy neurons in the phenomenon of induction (repeated subsequences in text). Panel (a) displays the activations, entropy, and loss in a model processing a repeated sequence. Panel (b) demonstrates the effect of ablating (silencing) individual entropy neurons on the resulting entropy. Neuron 11.2378 is highlighted as having a significant impact. Panel (c) explores the relationship between the activation of neuron 11.2378 and the activation of specific induction heads (parts of the model specialized for handling repeated sequences). Ablating induction heads reduces the activation of 11.2378, showing a connection between these components in the model’s processing of induction.
read the caption
Figure 5: Entropy Neurons on Induction. (a) Activations, entropy, and loss across duplicated 200-token input sequences. (b) The effect of clip mean-ablation of specific entropy neurons. Neuron 11.2378 shows the most significant impact, with up to a 70% reduction in entropy. (c) BOS ablation of induction heads: Upon the ablation of three induction heads in GPT-2 Small, the activation of entropy neuron 11.2378 decreases substantially.
🔼 This figure demonstrates the activity of token frequency neurons during induction tasks. Panel (a) shows the activations, entropy, and loss across duplicated input sequences. Panel (b) shows the effect of mean-ablating specific token frequency neurons, revealing their influence on entropy. Panel (c) provides a scatter plot illustrating the change in loss upon ablation of neuron 23.417, colored by reciprocal rank (RR). The results suggest that ablation tends to increase loss for tokens with initially low loss and decreases it for tokens with initially high loss.
read the caption
Figure 10: Token Frequency Neurons on Induction. (a) Activations, entropy, and loss across duplicated 200-token input sequences. (b) The effect of clip mean-ablation of specific token frequency neurons. (c) Scatter plot of loss changes per token post-ablation of neuron 23.417, colored by reciprocal rank (RR). Ablation tends to increase loss for low initial loss tokens and decrease it for high initial loss tokens.
🔼 This figure shows the relationship between the change in entropy and the change in prediction accuracy when ablating individual neurons in the final layer of a large language model. The x-axis represents the change in prediction accuracy after ablating a neuron, while the y-axis represents the absolute change in entropy. The red points highlight neurons whose effect is dependent on Layer Normalization (LN). The figure demonstrates that there is a set of neurons that significantly impact the model’s confidence (entropy), while having minimal direct effect on the model’s predictions. This suggests that these neurons are involved in regulating the model’s uncertainty.
read the caption
Figure 1: Entropy and Prediction. We mean ablate final-layer neurons across 4000 tokens and measure the variation in the entropy of the model's output Pmodel against average change of model's prediction (argmax Pmodel(x)). We identify a set of neurons whose effect depends on LayerNorm (red points; metric described in §3.2), and which affect the model's confidence (quantified as entropy of Pmodel) with minimal impact on the prediction.
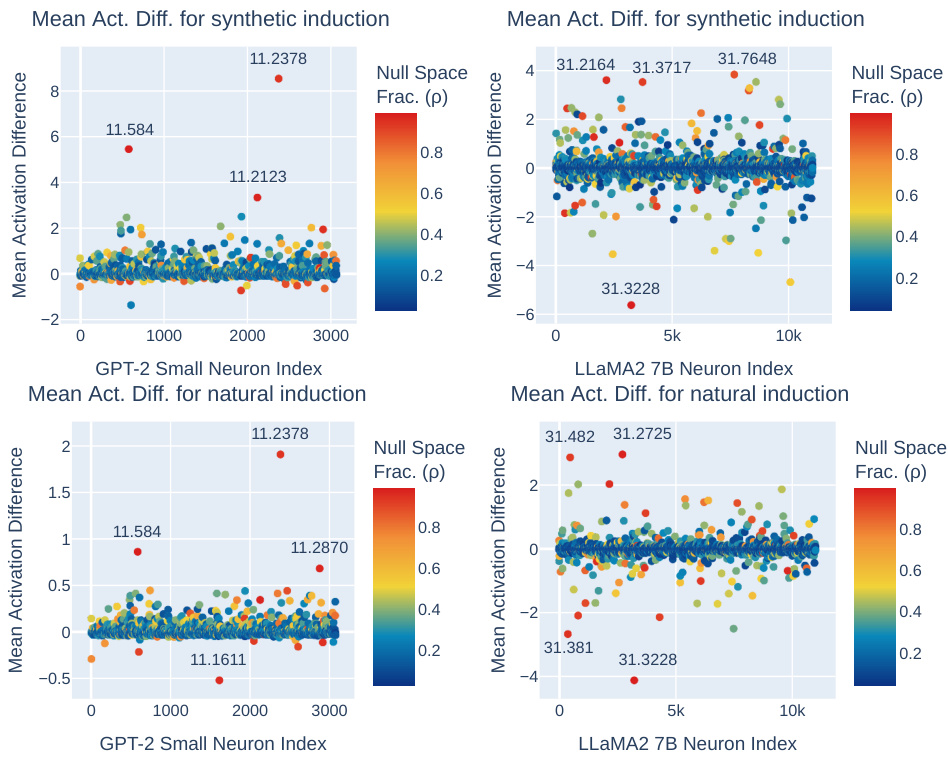
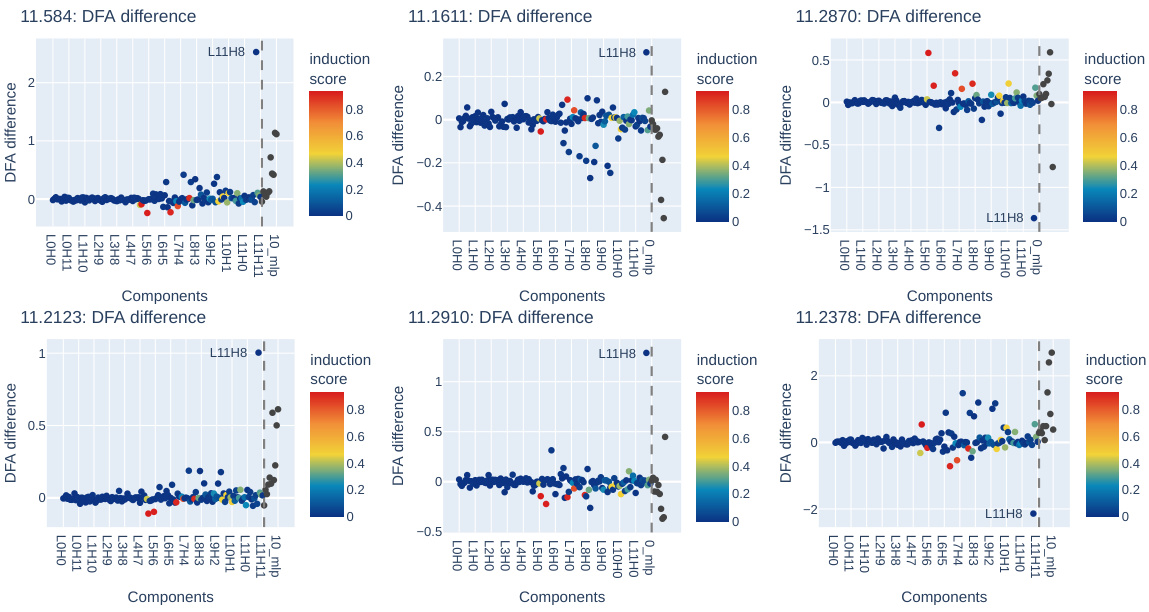
🔼 This figure compares the change in activation of neurons in GPT-2 small and LLaMa2 7B models during synthetic and natural induction. It shows that entropy neurons exhibit the largest activation change in both cases. Neurons with a high proportion of their norm projected onto the unembedding null space and a large change in activation are highlighted.
read the caption
Figure 11: Neuron activation differences for synthetic and natural induction: (left) GPT2-Small final-layer neurons (right) LLaMa2 7B final-layer neurons. Among final-layer neurons, entropy neurons exhibit the largest activation change for both synthetic and natural induction settings. Entropy neurons with especially high fraction of neuron norm in the null space (p) and large change in activation are labelled.
🔼 This figure shows the analysis of entropy neurons in GPT-2 Small and LLaMA2 7B. Panel (a) displays neurons based on weight norm and logit variance, identifying entropy neurons. Panel (b) illustrates the causal mediation analysis showing the total and direct effects of a neuron on the model’s output. Panel (c) compares the total and direct effects on model loss for entropy and randomly selected neurons. Panel (d) shows singular values and cosine similarity between neuron output weights and singular vectors of Wu (unembedding matrix). Panel (e) highlights entropy neurons’ significant LayerNorm-mediated effects and projection onto the null space. Panel (f) shows the LayerNorm-mediated effect in LLaMA2 7B, relating to the fraction of the neuron’s norm in the null space and the change in entropy upon ablation.
read the caption
Figure 2: Identifying and Analyzing Entropy Neurons. (a) Neurons in GPT-2 Small displayed by their weight norm and variance in logit attribution. Entropy neurons (red) have high norm and low logit variance. (b) Causal graph showing the total effect and direct effect (bypassing LayerNorm) of a neuron on the model's output. (c) Comparison of total and direct effects on model loss for entropy neurons and randomly selected neurons. (d) Singular values and cosine similarity between neuron output weights and singular vectors of Wu. (e) Entropy neurons (red) show significant LayerNorm-mediated effects and high projection onto the null space (p). (f) LN-mediated effect in LLAMA2 7B. p is computed with k = 40 ≈ 0.01 * dmodel. Color represents absolute change in entropy upon ablation (ΔH).
🔼 This figure examines the relationship between the fraction of a neuron’s weight norm projected into the null space of the unembedding matrix and the effect of LayerNorm on the model’s output. It shows that entropy neurons, characterized by a high weight norm and minimal direct effect on logits, significantly affect the model’s output distribution through LayerNorm. The ablation of an entropy neuron in LLaMA2 7B decreases entropy and increases losses on incorrect predictions, highlighting their role in confidence calibration.
read the caption
Figure 7: Entropy Neurons Across Different Models. Relationship between the fraction p of neuron norm in the Wu null space and the LayerNorm-mediated effect on model output for neurons in the last layer of various models. (a) Change in loss after ablation of entropy neuron 31.3228 in LLaMA2 7B. Ablation decreases entropy and increases loss on incorrect predictions.
Full paper#