TL;DR#
Many real-world systems, like ride-sharing platforms and online job markets, can be modeled as multi-server queueing systems where jobs arrive randomly and need to be assigned to servers. However, existing models often assume known service rates and ignore server preferences. This paper addresses the limitation of not knowing the service rates and server preferences by introducing preference feedback and a feature-based model for service rates.
The researchers developed novel algorithms, based on UCB and Thompson Sampling, that learn these unknown service rates and server preferences simultaneously while ensuring queue stability. These algorithms achieve sublinear regret bounds and keep the average queue length within acceptable limits. This work is a significant contribution to the field, addressing real-world complexities and offering a new tool for optimizing dynamic systems with unknown parameters and preferences.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in queueing systems and multi-armed bandits. It bridges the gap between theoretical models and real-world applications by incorporating preference feedback and features for service rates into queueing matching bandits. This work is especially relevant due to the increasing use of matching systems in diverse fields, opening up new avenues for research on stability and regret analysis in dynamic settings.
Visual Insights#

🔼 The figure illustrates the queueing matching bandit process with preference feedback. (a) shows jobs arriving randomly in queues (agents), with unknown utility values between queues and servers (arms). (b) depicts how a scheduler assigns each queue to a server. Finally, (c) demonstrates that each server stochastically accepts at most one assigned job based on its preference, serving the accepted job while rejected jobs remain.
read the caption
Figure 1: Illustration of queueing process with 4 queues/agents (N = 4) and 3 servers/arms (K = 3)

🔼 This table lists the notations used throughout the paper. It includes symbols for variables representing time horizon, number of agents and servers, feature dimensions, agent and server parameters, queue lengths, traffic slackness, service rates, arrival and departure rates of jobs, average queue lengths, regret, and other relevant quantities.
read the caption
Table 1: Notation Table.
In-depth insights#
Queueing Bandits#
The intersection of queueing theory and multi-armed bandits, known as “Queueing Bandits,” presents a powerful framework for modeling and solving problems where resource allocation decisions must be made under uncertainty and dynamically changing system conditions. This is particularly relevant in applications such as online platforms, cloud computing, and ride-sharing services, where jobs arrive at queues, and servers or workers must be assigned efficiently. The challenge lies in balancing the exploration of potentially better assignments with the exploitation of current knowledge to maintain queue stability and minimize delays. Effective algorithms require learning the unknown service rates or the latent utilities between jobs and servers while simultaneously optimizing the scheduling policies. Algorithms such as UCB and Thompson Sampling have been effectively adapted for these scenarios, but further research is needed to address the complexities of multi-class systems, preference feedback, and real-world constraints like limited server capacity. The inherent service rates are often modeled using feature-based functions, such as multinomial logit (MNL), capturing the preferences of servers, leading to more accurate and nuanced resource allocation strategies.
Preference Feedback#
The concept of “Preference Feedback” in a multi-server queueing system is crucial for real-world applicability. It acknowledges that server behavior isn’t solely determined by inherent service rates, but is significantly influenced by relative preferences over the jobs assigned. This feedback mechanism allows the system to learn dynamic service rates, reflecting the reality of situations like ride-sharing, where driver preferences impact service speed. The challenge lies in balancing exploration (learning preferences) and exploitation (optimizing queue stability). Algorithms utilizing this feedback must efficiently update models of server preferences while simultaneously ensuring queue stability and minimizing overall regret. The multinomial logit (MNL) model, often used to model choice behavior, becomes an important component of any algorithm incorporating preference feedback into the queueing process. Successfully addressing this aspect significantly improves the practical relevance and performance of queueing systems by enabling more accurate job assignment strategies.
MNL Model#
The Multinomial Logit (MNL) model, a cornerstone of discrete choice modeling, finds significant application in the paper’s framework for modeling the stochastic behavior of servers. Unlike simpler models, the MNL function elegantly captures the relative preferences of servers over multiple assigned jobs, reflecting real-world scenarios where service rates are influenced by the relative desirability of tasks. This nuanced approach moves beyond assumptions of constant service rates or simplistic assignment policies, enhancing the realism and practical applicability of the theoretical framework. The utilization of an MNL function within a queuing matching bandit setting presents a novel and sophisticated approach that requires careful consideration of the model’s inherent assumptions and limitations, particularly regarding the independence of irrelevant alternatives (IIA) property and its potential impact on the accuracy of predictions. The feature-based approach, where agents’ service rates are modeled based on known features, further enhances the model’s generalizability and predictive power. However, model parameter estimation remains a challenge in an online learning context, demanding computationally efficient algorithms that maintain stability while learning the unknown parameters of the MNL model.
Stability Analysis#
A rigorous stability analysis is crucial for assessing the performance of queueing systems. This involves demonstrating that the system’s queue lengths remain bounded over time, preventing unbounded growth. The choice of Lyapunov function is critical, as it dictates the analytical approach. Methods often employ drift conditions to show that the expected change in the Lyapunov function is negative when queue lengths exceed a certain threshold. This implies that the system is strongly stable, as opposed to just mean rate stable. The analysis often considers a tradeoff between exploration and exploitation in online scenarios, impacting the rate at which stability is achieved. Regret analysis is also often interwoven with stability analysis, quantifying the performance loss due to the lack of perfect knowledge about service rates and preferences. Ultimately, a successful stability analysis provides strong guarantees on the system’s behavior under various conditions, ensuring its robustness and efficiency.
Future Works#
The research paper’s ‘Future Works’ section could explore several avenues. Extending the theoretical analysis to incorporate more sophisticated queueing models or to consider more complex scenarios would strengthen the work. Empirically, investigating the algorithms’ performance under diverse real-world conditions with preference feedback is crucial. Developing more efficient algorithms for large-scale applications by addressing the computational complexity associated with preference learning and combinatorial optimization is a key area. Finally, applying the framework to other domains where queueing and preference modeling are relevant—such as ride-sharing or online marketplaces—would broaden the impact and demonstrate the algorithm’s generalizability. Addressing the limitations in the current model, such as simplifying assumptions about job arrival and service rates, would enhance the model’s realism and robustness.
More visual insights#
More on figures
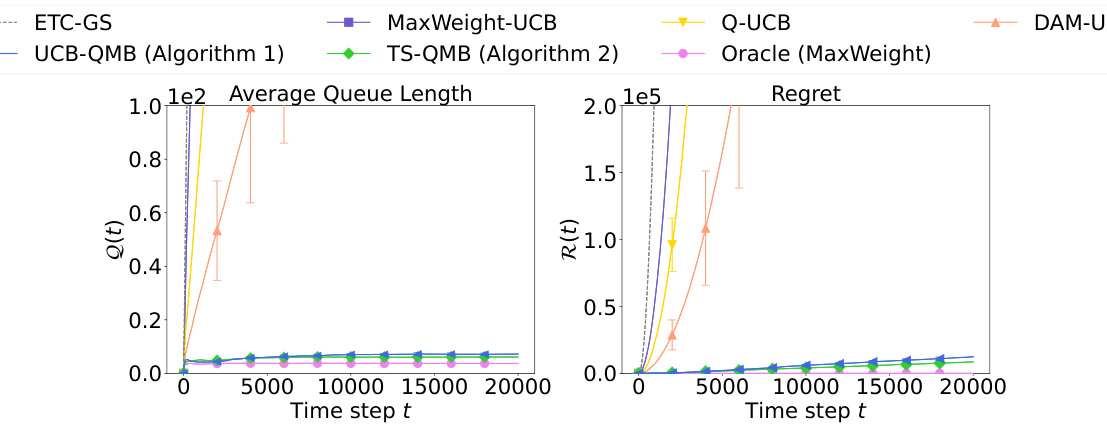
🔼 The left plot shows the average queue length over time for the proposed UCB-QMB and TS-QMB algorithms, compared to several baselines (MaxWeight-UCB, Q-UCB, DAM-UCB, and ETC-GS). The proposed algorithms exhibit significantly lower average queue lengths, demonstrating their effectiveness in stabilizing the queueing system. The right plot shows the cumulative regret for the same algorithms and baselines, revealing that the proposed algorithms achieve sublinear regret compared to the baselines, indicating their efficiency in learning the optimal scheduling policy. Error bars represent standard deviation.
read the caption
Figure 2: Experimental results for (left) average queue length and (right) regret
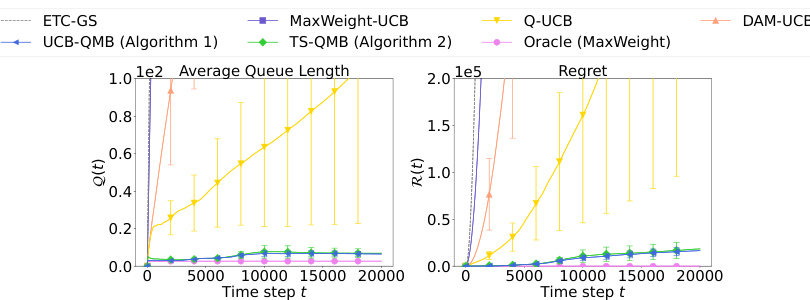
🔼 The figure presents the experimental results for two key metrics: average queue length and regret. The left panel displays the average queue length over time, comparing the performance of several algorithms (UCB-QMB, TS-QMB, MaxWeight-UCB, Q-UCB, DAM-UCB, ETC-GS) against an oracle (MaxWeight). The right panel shows the cumulative regret of the same algorithms. Error bars (standard deviation) are included to represent the variability of the results. The results demonstrate the stability and regret performance of the proposed algorithms (UCB-QMB and TS-QMB) compared to the other approaches.
read the caption
Figure 2: Experimental results for (left) average queue length and (right) regret
Full paper#



















