TL;DR#
Current research extensively studies neural networks, especially focusing on their computational capabilities. However, most studies focus on Boolean functions, neglecting the power of real-valued computations used in real-world applications. This is particularly relevant to Graph Neural Networks (GNNs), which are increasingly used but lack rigorous analysis of their computational power beyond Boolean contexts.
This paper bridges this gap by directly comparing GNNs to arithmetic circuits over real numbers. It proposes a novel Circuit-GNN (C-GNN) framework to rigorously analyze the computational power of GNNs. The main finding is that the expressiveness of GNNs is exactly equivalent to that of arithmetic circuits over real numbers, with the GNN’s activation function acting as a gate type in the corresponding circuit. This holds for various common activation functions and depth-constant networks.
Key Takeaways#
Why does it matter?#
This paper is crucial because it establishes a clear link between the computational power of Graph Neural Networks (GNNs) and arithmetic circuits. This connection provides new tools for analyzing GNN expressivity, which is critical given their increasing use. Understanding these limits helps design more effective GNN architectures and avoid unnecessary scaling, fostering more efficient and powerful machine learning models. The uniformity results ensure broad applicability across GNN architectures.
Visual Insights#

🔼 This figure shows an example of how a simple arithmetic circuit (a) can be simulated by a C-GNN (b). The circuit consists of three input gates, an addition gate, and a multiplication gate. The C-GNN has the same structure as the circuit, with each gate in the circuit represented by a node in the C-GNN. The feature vectors of the nodes in the C-GNN represent the values of the gates in the circuit. The computation of the C-GNN simulates the computation of the circuit, with the values of the gates in the circuit being calculated by the nodes in the C-GNN. This illustrates the equivalence shown in Theorem 3.11 between C-GNNs and arithmetic circuits of constant depth.
read the caption
Figure 1: Example illustrating the proof of Theorem 3.11.
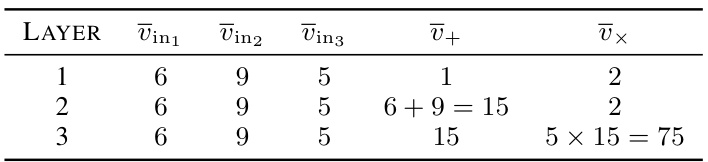
🔼 This table demonstrates the step-by-step computation of a C-GNN (Circuit Graph Neural Network) used to simulate a simple arithmetic circuit. Each row represents a layer in the C-GNN, showing the evolution of feature vectors for input gates (vin1, vin2, vin3) and gates performing addition (+) and multiplication (x) operations. The final layer shows the result of the computation, mirroring the output of the simulated arithmetic circuit.
read the caption
Table 1: Example illustrating the proof of Theorem 3.11: The values of the feature vectors during the computation of the C-GNN.
Full paper#


















